采用幅度相移键控调制的分层空间调制算法

李云风, 王磊, 王志成

(西安交通大学电子与信息工程学院, 710049, 西安)

多输入多输出(MIMO)技术既可以通过空间复用来提高系统的容量,又可以通过空间分集来提升系统的可靠性,因而近年来获得了广泛的研究。但是,MIMO技术在带来各种增益的同时,也存在着系统复杂度高和硬件实现中射频单元成本高等一些缺陷。随着MIMO传输技术的深入研究,Mesleh等人于2008年提出了空间调制(SM)技术[1],创造性地提出了多天线调制中不仅可以利用幅度相位调制(APM)符号传输信息,而且可以利用天线索引号来传递额外的信息。SM技术在同一个时隙中只需激活一根天线来发送信号,其余天线保持静默状态,因而能够有效地避免MIMO方案中诸如天线间同步、信道间干扰以及射频链路多等问题。文献[2-3]提出的空移键控(SSK)技术作为一种简化的SM传输技术,仅利用空间维度携带信息,具有较低的检测复杂度。然而,SM/SSK的频谱效率都与发射天线数呈对数关系,因而不能获得很高的频谱效率。为了提高SM的频谱效率,很多研究者提出了不同的改进方案。文献[4-7]通过在发射端采用多根发射天线组合的方式来发送信号,分别提出了广义空移键(GSSK),广义空间调制(GSM)和多天线激活-空间调制(MA-SM)。GSSK方案通过同时激活多根天线,仅利用空间维度来增加系统的频谱效率。MA-SM方案通过在每一个时隙同时激活多根发射天线来传输不同的调制符号以提高系统的频谱效率。文献[8]通过额外的调节空间维度,将复信号分解然后扩展到同相和正交维度,提出了正交空间调制(QSM),实现了发射天线同步并增强了传输性能。文献[9]通过扩展星座中星座点的个数,提出了一种扩展空间调制(ESM)方案,有效地提升了系统的频谱效率,并在文献[10]中进行了完善。文献[11]为了更好地利用空间维度来发送信息,提出了分层空移键控(LSSK)方案,利用分层结构,通过增加SSK传输层的数目来提高SM的频谱效率。

本文为了提高SM的频谱效率,提出了一种基于APSK的分层SM(LSM)算法。LSM算法通过不同层发射来自不同振幅的PSK星座点来发送多层SM信息,灵活地调节激活天线的个数,使SM的频谱效率随着层数的增加呈线性增长。此外,为了进一步降低系统的误比特率(BER),对于一个特定的MIMO系统,本文提出了一种有效的算法,来确定APSK的内外环幅度比。最后,本文通过接收端将激活天线索引号和调制符号单独检测,提出了一种低复杂度译码算法,可以有效地降低译码复杂度。

1 系统模型

对于一个具有Nt根发射天线和Nr根接收天线的MIMO系统,设其在一个时隙发射Nt×1维信号s,则Nr×1维接收信号y可表示为

式中:ρ是发射端总的发射功率;L表示总层数,1≤L≤Nt;H和n分别表示Nr×Nt维的信道矩阵和Nr×1维加性高斯白噪声(AWGN)向量,H和n中的元素均服从均值为0、方差为1的独立复高斯分布。

2 本文所提LSM算法

2.1 LSM算法系统模型

考虑一个采用LSM调制的MIMO系统,L层的LSM发送信号s表示为

s=[0 …xi…xL…x1… 0]T

(2)

图1 2-APSK调制的星座图

图1给出了M=2、L=2时的APSK调制的星座图。第1层发送幅度为r1的PSK调制符号,第2层发送幅度为r2的PSK调制符号,并且相比于幅度为r1的PSK星座旋转了π/Mrad。

因为每根激活天线发送一层SM信号,每层发送比特数为lbQ+lbM,所以LSM的频谱效率为L(lbQ+lbM)。其中Q是每层天线个数,并且有

Nt=Q+L-1

(3)

表1给出了在不同发射天线数下,M=4,L=2时,本文LSM算法与其他几种算法频谱效率的比较。

表1 不同发射天线下5种算法的频谱效率比较

由表1可以发现:相比较于LSSK算法,本文LSM算法通过加入调制符号可以获得更高的频谱效率;当发射天线为3、5和6时,LSM算法频谱效率比GSM高1 b/(s·Hz);相比较于QSM、ESM算法,LSM算法对于任意发射天线数都适应并且可以灵活地调节激活天线的个数。

2.2 LSM比特映射

2.2.1 LSM算法层映射 将待发送比特数据串并转换得到比特块g(n)=[b1b2…bj…bLlb(QM)],g(n)含有的比特数是L(lbQ+lbM),其中bj是每个比特块中的第j个比特,bj等于0或1。然后将比特块g(n)分成L层平行比特数据块p(n),p(n)=[b1b2…bi…bL]T,其中bi是第i层,含有(lbQ+lbM)个比特。

2.2.2 LSM算法比特映射 首先确定MIMO系统符号调制阶数M和层数L,然后对Nt根发射天线进行编号{1,2,…,Q,…,Nt},其中Q由式(3)确定。

(1)第1层SM映射。将第1层比特数据块b1分为两部分,前m1=lbM个比特用来选取幅度为r1的PSK星座点,即调制符号x1,剩余m2=lbQ个比特用来选取激活天线天线索引号a1,即从索引号为{1,2,…,Q}的Q根备选发射天线中选择激活天线的索引号a1。

(2)第2层SM映射。将第2层比特数据块b2分为两部分,前m1个比特用来选取幅度为r2的PSK星座点x2,剩余m2个比特用来选取激活天线的索引号a2。因为第1层已经选择了索引号为a1的天线,所以第2层选择激活天线时要排除索引号为a1的天线。同时,为保证第2层备选天线数仍为Q,增加1根索引号为Q+1的天线,即从索引号{1,2,…,a1-1,a1+1,…,Q+1}的Q根备选发射天线中选择激活天线的索引号a2。

(3)第i层SM映射。将第i层比特数据块bi分为两部分,前m1个比特用来选取幅度为ri的PSK星座点xi,剩余m2个比特用来选取激活天线的索引号ai。因为前i-1层已经选取了索引号为{a1,a2,…,ai-1}的天线,所以第i层进行激活天线选择时要排除{a1,a2,…,ai-1}这些索引号的天线。即从索引号为{1,2,…,Q+i-1}的(Q+i-1)根天线中去掉索引号为{a1,a2,…,ai-1}的i-1根天线后,剩余的Q根天线中再选择激活天线索引号ai。

(4)依次类推,直到第L层。最后经过L层调制后,就确定了总的天线激活索引号和调制符号。

3 性能分析

本节首先对LSM算法的误码性能进行分析,并以系统误比特率上界为目标函数给出PSK内外环幅度比选择准则,最后将激活天线索引号和调制符号单独检测,提出了一种低复杂度的译码算法。

3.1 LSM最优检测算法误码率

这一小节推导LSM系统的误比特率上界。根据文献[12],采用最大似然(ML)译码时LSM算法的误比特率可写为

式中:γ=2L(lbQ+lbM)为所有可能的发送信号总数;Ne,B(sκ→sλ)是信号sκ和信号sλ之间的错误比特数;p(sk→sλ)表示发送信号sκ被误判为信号sλ的概率。根据文献[12],条件差错概率为

p(D>0)

(5)

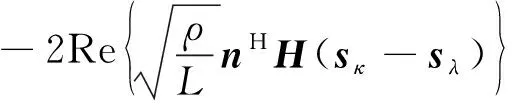
(7)

利用Q(x)≤(1/2)exp(-x2/2),则式(7)中差错概率上界为

将式(8)代入式(4)可得LSM算法的误比特率上界为

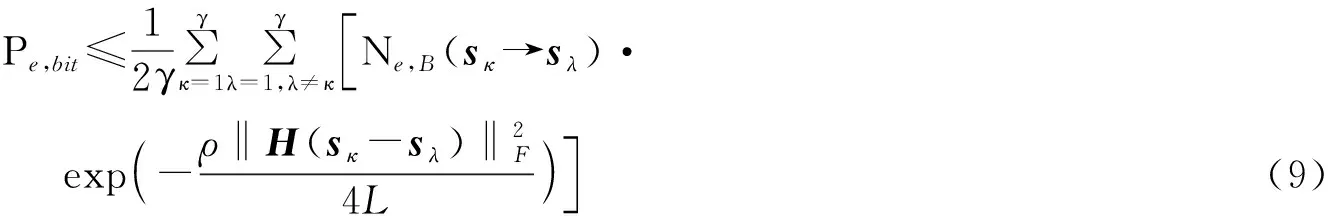
3.2 PSK内外环幅度比算法

如图1所示,APSK星座的内外环比α=r2/r1,α的取值有无限多个。以误比特率上界为目标函数通过搜索最小值来确定最优内外环幅度比[13]

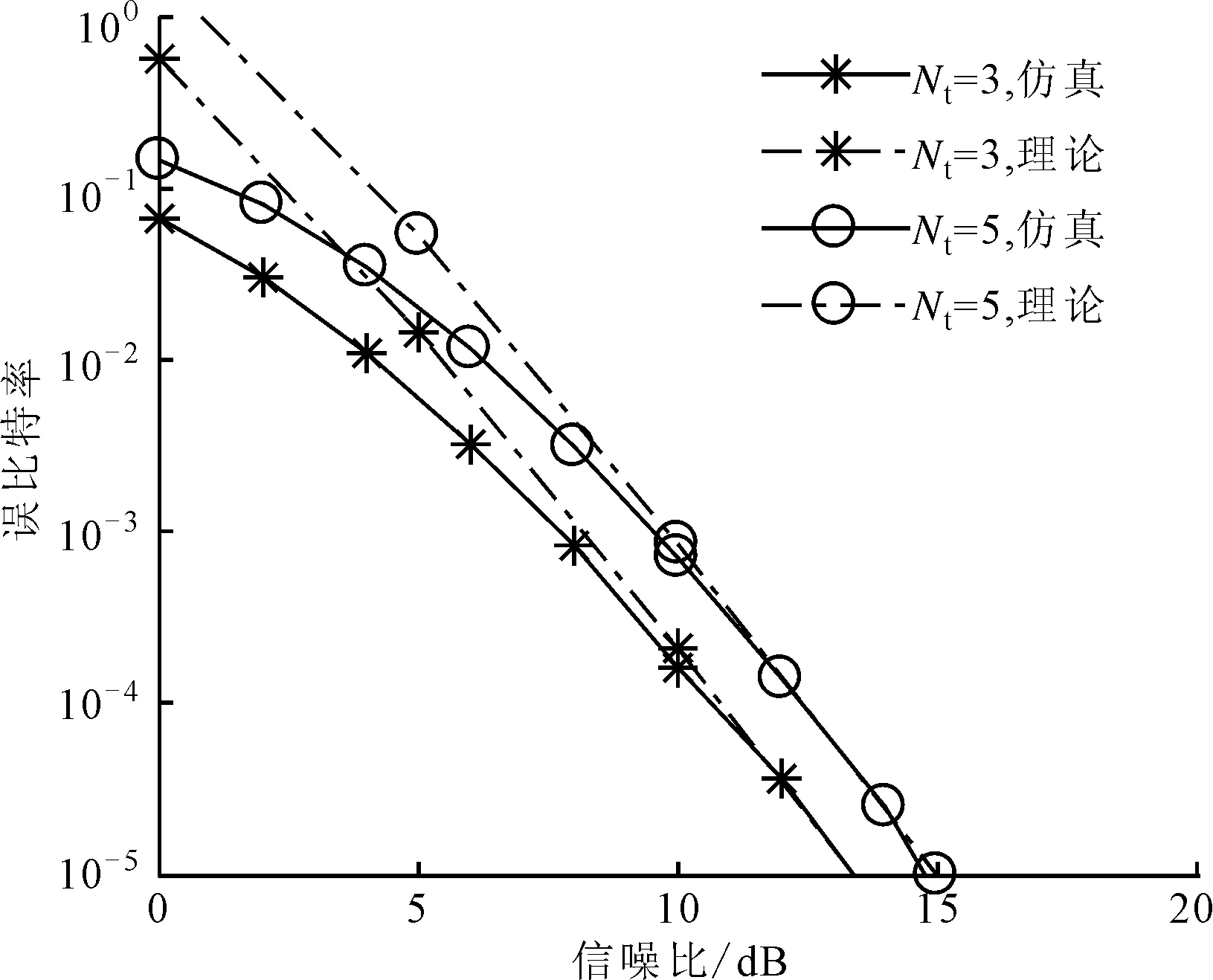
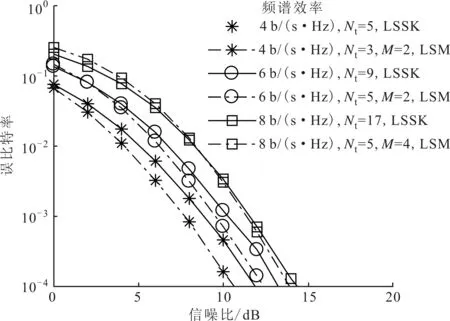
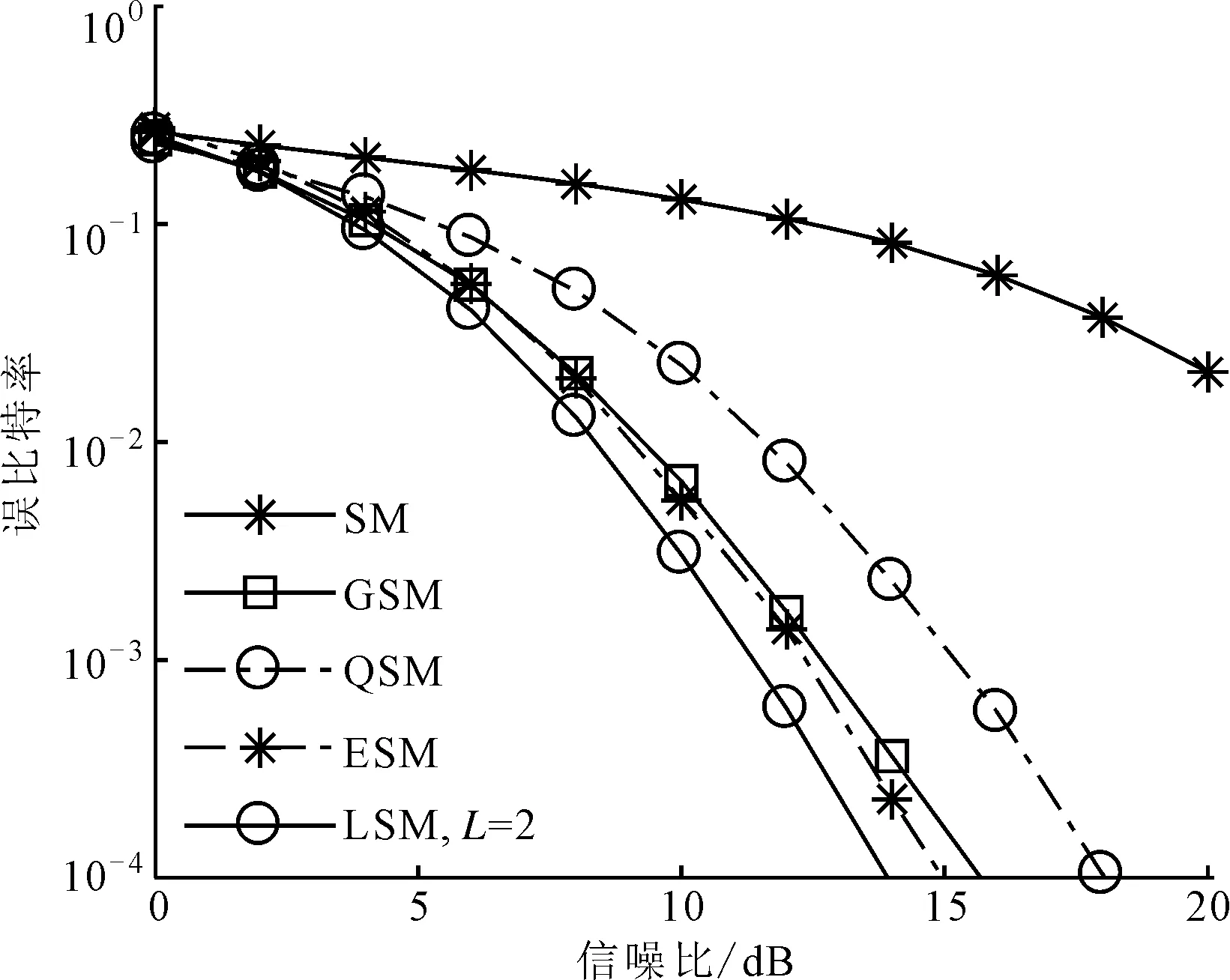
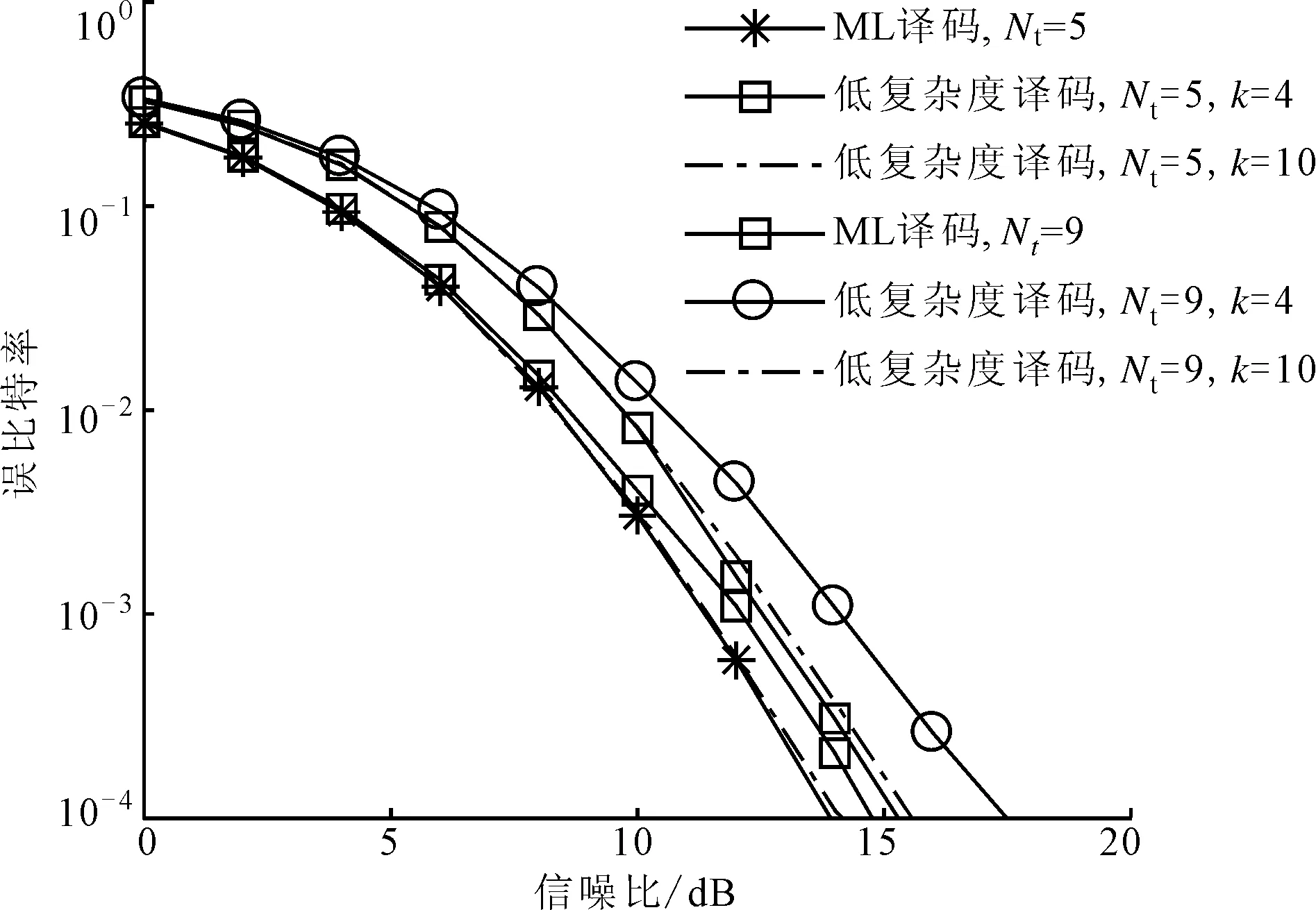
确定MIMO系统的参数Nt、Nr、M、Q、L和一个较高的信噪比(RSN),则α的搜索范围1<α

(1)1<α

(2)n*=min{P(n)}即为最优解,此时最优内外环比α*=1+n*Δα。

在上述步骤中,对于一个特定的系统来说,信噪比的取值是可变的。如果信噪比的取值较小,则可能会因为噪声的原因而得不到理想的内外环幅度比,因此这个算法在信噪比较大时是有效的。同时考虑到在信噪比取到某个较大值时,随着信噪比的增加,α*是不变的,所以Uupper=3是一个较为合理的值[13]。如果Uupper值设置较小,则可能得不到最优解;如果较大,则会增加搜索的计算复杂度。

图2给出了在信噪比为15dB、取内外环幅度比α在1～3范围时,不同系统配置的误比特率,接收天线个数为4,层数为2。由图2可知,当Nt=3,M=4时,α*=1.2;当Nt=5,M=4时,α*=1.1;当Nt=5,M=8时,α*=1.6。

图2 不同系统配置的误比特率

3.3 接收端低复杂度译码算法

ML译码算法对激活天线的索引号和调制符号联合译码,因此具有较高的复杂度。针对本文算法的特点,提出了一种将天线索引号和调制符号独立检测的低复杂度译码算法。

根据式(1),Nr×1维接收信号可表示为

式中:hai表示第i层信号经过的Nr×1维的信道向量,同时也是信道矩阵H的第ai列。

式中:dr为升序排序后的第r个值;sort(·)表示排序。

(2)调制符号检测。为了避免因各个信道向量不正交而使得系统性能较差的问题,本文选取式(12)中前k个值来进行激活天线检测和调制符号的联合检测,1≤k≤K。k的值决定了系统性能和复杂度之间的权衡。由式(12)中前k个较小的值,得到相应的k个子空间侯选集,则第i个子空间侯选集Ri可表示如下

式中:hi为信道矩阵H的第i列,i=1,2,…,L。

因为每个信道传送的调制符号来自不同幅度的星座点,所以根据调制符号就可以判断信道选择次序。在侯选集中做最大似然检测算法来确定调制符号,公式如下

表2和表3分别给出了ML译码算法和本文提出的低复杂度译码算法的每一步的计算次数及计算复杂度,其中计算复杂度由运算过程中所需的浮点数来衡量。

表2 ML算法的计算复杂度

表3 低复杂度译码算法的计算复杂度

以Nt=129、Q=128、L=2、Nr=4、M=16的系统为例[11],当k=4时,ML检测的计算复杂度是167772160,本文低复杂度译码算法检测的计算复杂度是2789888,只有ML检测算法的1.66%,因此在发射天线数较多及参数k较小时,本文低复杂度译码算法可以有效降低计算的复杂度。

4 仿真结果与讨论

为了验证所提算法的有效性,本节对SM、LSSK、GSM、QSM、ESM和LSM算法的误比特率性能进行了仿真,并对仿真结果进行了比较。仿真均假定各天线之间的信道是相互独立的,并且服从CN(0,1)分布,不同方案的接收天线均设为4。

图3给出了Nt=3、Q=2、L=2、M=4和Nt=5、Q=4、L=2,M=4时,本文LSM的理论上界与蒙特卡洛方法仿真结果比较。由图3可以看出,在高信噪比的情况下理论分析结果能够很好地吻合仿真结果,从而证明了理论分析的正确性。

图3 本文LSM算法的理论和仿真比较

图4 LSSK与LSM性能比较

图4给出了当层数L=2时,LSSK和LSM算法的误比特率仿真曲线。由图4可以看出,当频谱效率为4b/(s·Hz)和6b/(s·Hz)时,LSM算法的发射天线个数不仅比LSSK算法少,性能也优于LSSK算法。其主要原因是由于LSM算法加入了符号调制,使得LSM算法有更高的频谱效率,同时当频谱效率为8b/(s·Hz)时,LSM和LSSK算法的性能基本一致,但是LSM比LSSK算法节省了12根发射天线,从而节约了硬件资源。

图5给出了本文LSM算法与SM、GSM、QSM、ESM算法在相同的天线配置与频谱效率下,采用最大似然检测的仿真结果。由图5可以看出,LSM算法的性能明显优于其他算法。这是因为LSM采用APSK信号不仅能够区分各层而且还能够获得较大的欧式距离,从而更好地利用空域传输信息。

图5 本文LSM算法与其他4种算法的性能比较

图6给出了ML和本文低复杂度译码算法的性能比较。其中,低复杂译码算法的参数k分别为4和10。由图6可知,低复杂度译码算法表现出近最大似然算法的性能,并且随着低复杂度译码算法的k值的增加,低复杂度译码算法与ML性能基本一致。其主要原因是误差个数k增加时需要更多的候选子空间,当k等于总的子空间个数K时也就等价于ML检测。

图6 本文低复杂度译码算法与ML译码算法的性能比较

图7给出了本文低复杂度译码算法取不同k值时误比特率仿真比较。由图6和图7可知,在低信噪比情况下,低复杂度译码能够在获得接近ML检测性能的同时有效地降低了检测复杂度。在高信噪比时,低复杂度译码算法通过增加k值仍能获得接近ML检测的性能。

图7 不同k值下低复杂度译码算法的性能比较(Nt=9)

5 结束语

针对空间调制频谱效率较低的问题,本文提出了一种基于幅度/相移键控的分层SM算法——LSM算法通过。该算法加入分层结构来发射多层SM信息,有效地提高了系统的频谱效率。同时,以系统误比特率上界为目标函数,提出了一种优化算法来确定APSK内外环幅度比。最后,将激活天线索引号和调制符号单独检测,提出了一种低复杂度译码算法。理论分析和仿真结果表明,在相同频谱效率下,本文LSM算法的性能优于现有的GSM、QSM、ESM等算法。