人体模型网格孔洞的快速修复方法

刘世凡, 梁晋, 董波

(西安交通大学机械制造系统工程国家重点实验室, 710049, 西安)

近年来,3D反求技术发展迅速,快速三维人体扫描广泛应用于医疗外科、服装、个性化定制等行业,因此快速获取完整的人体三维模型数据具有重要的意义[1]。但是,人体扫描结果几乎不可避免地会出现局部信息缺失,从而产生模型孔洞,对人体模型的整体外观和后续处理产生巨大的不良影响[2],其中尤以大面积信息缺失所致的孔洞影响最深[3]。因此,在保证模型特征的情况下快速修复大面积复杂孔洞是三维模型后处理过程中的重要工作。

Davis等在孔洞附近设置符号距离函数,通过扩散来重建整体模型,该方法修复精度较高但效率低[4]。Van等通过将三维点映射到二维平面并进行德洛内三角化来修补孔洞,但难以修补空间形状复杂的孔洞[5]。Centin等通过泊松驱动来封闭孔洞,但是需要依赖精确的顶点法线[6]。Brunton等利用最小能量方程获取投影平面并插入新点,但边界点数较多时,效率大大下降[7]。Altantsetseg等通过边界边轮廓线获取均匀插入点,同样存在效率问题[8]。Brunet等利用B样条曲线获取插入点信息,该方法体素化过程较为耗时[9]。张立国等采用径向基函数拟合孔洞的隐式曲面,并将新增点投影上去,该方法对单一简单孔洞修补较为理想,但对大面积孔洞拟合隐式曲面效率很低且可能拟合失败[10]。Xia等通过特征线将孔洞分割后再修补,该方法依赖恰当的阈值[11]。刘震等通过动态规划构建曲面并利用带特征线约束的双拉普拉斯系统修补孔洞,方法保持了较好的细节但孔洞面积大时效率较低[12]。Wang等通过粒子群优化算法在三次曲面上获取新增点信息,该方法依赖优良的参数[13]。Wei等通过积分法产生最小三角面片来修补孔洞,但效率较低[14]。Hu等在细分三角面片后利用双边滤波重建缺失的特征,但生成的网格与原网格有较大差别[15]。高旋辉等先对孔洞进行异常值消除,再利用改进的多边形三角化法进行修补[16]。以上算法在孔洞修复精度方面有较大改进,但多应用于单一孔洞,而人体扫描模型中存在大量大面积且空间形状复杂的孔洞,这些方法难以快速甚至无法完成修补。

本文提出了一种利用边界点周围矢量信息建立权函数的孔洞修复算法,实现了对大面积复杂孔洞的快速、保持特征的均匀网格修补。该方法基于波前法,结合边界点法向量、边界点曲率和周边局部边界点聚拢方向建立权函数,通过最小化权函数确定新增点的空间坐标以产生新增面片,多次向孔洞内部推进直至孔洞修复完成。

1 传统波前法

传统波前法以递归的方式修补网格孔洞。首先用当前边界点集初始化波前,而后计算相邻边界边形成的内角,从最小内角开始递归推进,每次递归后都以新边界点集对波前进行初始化,直至孔洞被新增三角面片完全填充。对最小内角θ进行推进时,通常根据最小内角的大小采取不同的推进策略[17],当最小角θ<75°,直接连接边界点;当75°≤θ≤135°,新增点Vadd在θ角平分线上;当135°<θ≤180°,新增点Vadd1和Vadd2在θ角三等分线上,新增边长度取Vi点邻边的平均长度,如图1所示。

(a)0°≤θ<75° (b)75°≤θ≤135° (c)135°<θ≤180°图1 最小角推进原则

波前法可以快速地修复趋于收拢的简单孔洞,但无法保持孔洞特征,且当孔洞趋于发散时,孔洞修补会失败。这是因为波前法的推进方向仅由最小内角决定,当推进方向不朝向孔洞中心时,新增的三角面片不能聚拢并封闭孔洞。图2a、2b分别表示了趋于聚拢和趋于发散的孔洞在波前法迭代一次时的推进方向。

(a)趋于聚拢的孔洞 (b)趋于发散的孔洞图2 两种孔洞的波前法推进方向

本文采用了波前法的最小角迭代推进原则,但在推进策略上先通过边界点周边的聚拢矢量对大面积孔洞边界点法向量进行修正,再通过修正后的顶点法向量与边界点的两个邻点计算平均曲率,最后结合原插入向量建立加权函数,通过求解最小化的加权函数,得出新增点的空间坐标,使新增面片在孔洞趋于发散的情况下能够快速向孔洞中心聚拢。

2 网格孔洞修补

首先,通过孔洞边界点个数识别大面积的孔洞,对此类孔洞通过周边边界点的平均聚拢特征向量修正最小角顶点的法向量;然后,结合边界顶点局部曲率和原插入向量,建立并求解最小化加权函数,以获取新增点空间坐标,迭代推进直至网格封闭。本文算法适用的网格模型为流形网格模型。

对于任意孔洞,现定义边界点按逆时针顺序编号形成的集合为{Vi|i=0,1,…,nhole-1},其中nhole是孔洞边界点总个数;定义vij为边界点Vi指向边界点Vj的向量,vij的单位向量为eij。现以最小内角∠Vi-1ViVi+1=θ,75°≤θ<135°为例,此时应新增1个点Vx。

2.1 顶点法向量修正

本文以边界点个数大于50的孔洞为大面积孔洞。对于大面积孔洞,为避免新增面片不能聚合收拢,利用顶点Vi的局部聚拢方向对其法向量进行修正。以顶点Vi在边界点链表中指向前n个边界点和后n个边界点的单位向量的平均向量为局部聚拢方向,即计算单位向量

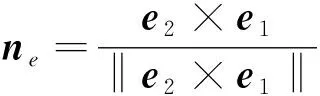
nr=αn0+βne

(2)

式中:n0为Vi原法向量,α+β=1,本文取α=0.85。

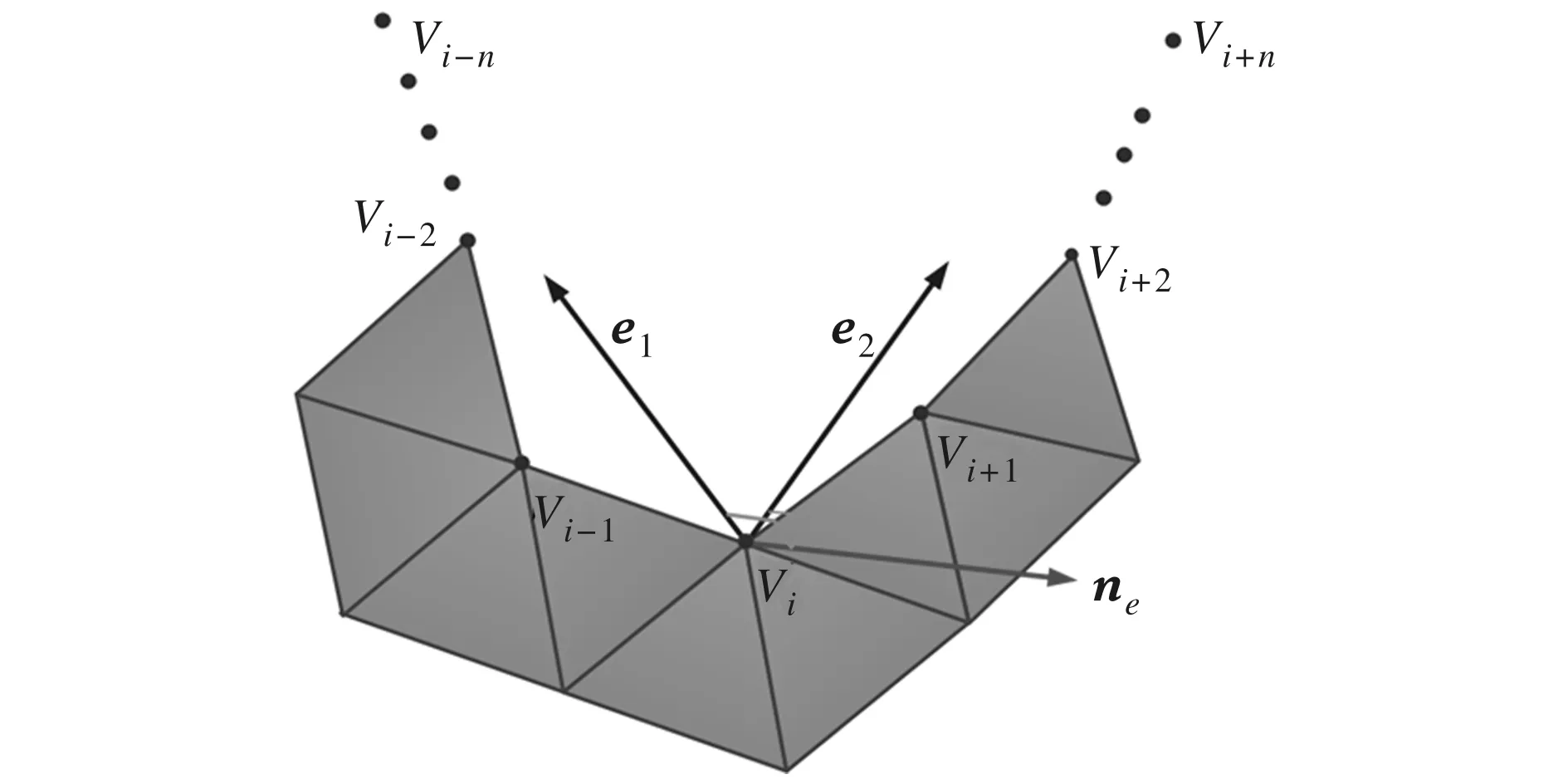
图3 法向量的修正向量ne

2.2 权函数

确定新增点Vx的空间坐标实质是确定顶点Vi指向Vx的向量vix,该向量应包含Vi点的局部曲率特征信息、收拢趋势信息,并能使新增的三角面片更规则。因此,本文建立了一个包含以上信息的权函数并求解,以获取新增点最优的空间坐标,具体步骤如下。

(1)先通过Vi-1点和Vi+1点的平均Taubin曲率计算Vi的曲率,Vi的Taubin曲率为

式中:nr为顶点Vi的修正法向量,向量T为vix在顶点Vi切平面上的投影。

(2)计算原插入向量

vip=lave(ei(i-1)+ei(i+1))

(4)

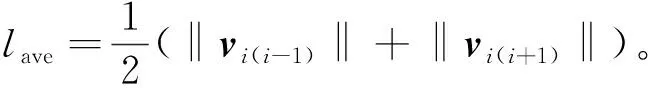
(3)结合原插入向量和局部曲率建立加权函数

式中:ω1+ω2=1(本文取ω1=0.65)。

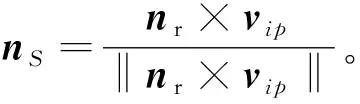
图4 局部平面极坐标

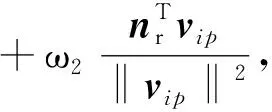
(5)最后,可得插入向量vix=laveRnr,其中R为绕nS逆时针旋转φ角的旋转矩阵。

当需要新增2个点时,算法基本过程同上,只需对新增的两个向量分别进行求解即可。对于非大面积孔洞,Vi的法向量无需修正。每次推进后,都以当前边界点集更新波前,直到修补完成。

本文通过表征顶点周边局部聚拢趋势的向量来修正顶点的原法向量,使得推进方向向孔洞的中心聚拢,从而可以快速修补趋于发散的大面积孔洞。结合边界点邻点的平均曲率和原插入向量建立加权函数,利用局部平面极坐标求解函数值最小时的新增向量与顶点修正法向量间的夹角,获得最终的新增向量,因此新增向量既保持了局部曲率,又使新增三角面片均匀规则。

3 实验及结果

为验证本文算法的孔洞修补效果,在主频3.3 GHz、内存8 GB的计算机上,利用VS2013开发网格修补软件,并对球模型和XTBodyScan快速人体扫描系统扫描的人体模型进行网格修补。

图5a存在缺失部分的球模型,图5b、5c、5d分别为传统波前法、隐式曲面法[10]和本文波前法修补结果。从图中可以看出,传统波前法仅仅封闭了模型,而本文算法和隐式曲面法都保持了较好的特征。

图6a为人体扫描模型头部截取部分,该模型的孔洞有153个边界点且孔洞趋于发散,传统波前法无法修补该孔洞。图6b是隐式曲面法修补人头模型孔洞的结果;图6c是隐式曲面法生成的新增三角面片,修补结果出现了大量自相交的三角面片,这是因为该孔洞趋于发散,拟合出的隐式曲面难以符合孔洞的收拢趋势,同时也导致了投射到隐式曲面上新增点不均匀,从而产生不均匀的三角面片。图6d是本文算法修补结果;图6e显示本文算法新增的三角面片大小均匀,形状规则;图6f是本文算法的局部细节情况,可见新增面片与原孔洞边界面片间有良好的过渡。

图7a为人体足部扫描模型,足底孔洞有319个边界点,孔洞空间形状复杂且趋于发散。传统波前法和隐式曲面法皆无法修补该孔洞。图7b、7c分别为本文算法修补后的新增面片及局部细节,修补后的新增面片均匀规则,且与边界面片过渡处光滑自然。

图8a为人体全身扫描模型,该模型中有孔洞196个,其中大面积孔洞11个。图8b为本文算法修补结果,图8c为部分孔洞修补细节,修补整个模型仅耗时26.8 s,且保持了孔洞的局部特征。

表1统计了以上6个孔洞的修补信息。三角形品质因子Q为三角形最短边与外接圆半径比,三角形越接近正三角形,则Q越接近1.73。本文以Q大于1.39的三角面片为高品质三角形[18],统计其与新增面片总数的比值。从表中可以看出,本文算法修补各类孔洞所产生的三角面片中,高品质面片都在90%以上,且修补时间短,效率高。

(a)球模型 (b)传统波前法 (c)隐式曲面法(d)本文算法图5 不同方法球模型修补效果对比

(a)头部模型 (b)隐式曲面法修补效果 (c)隐式曲面法新增面片

(d)本文算法修补结果(e)本文算法新增面片 (f)本文算法修补细节图6 不同方法头部模型修补结果对比

(a)足部模型 (b)新增面片 (c)局部细节图7 足部扫描模型修补结果

(a)原始模型 (b)修补结果

(c)孔洞1修复细节 (d)孔洞2修复细节 (e)孔洞3修复细节图8 人体全身模型

孔洞新增点数新增面片数修补时间/s高品质面片与新增面片之比/%球孔洞521250.04794.41头部孔洞2 1924 5391.18399.10足部孔洞4 97210 2833.16297.53孔洞19892 1750.60793.68孔洞24299900.34690.51孔洞31333160.13693.35

4 结 论

(1)本文算法对于边界点数超过50的孔洞,在迭代推进中对最小内角的顶点进行了法向量修正。利用顶点前后局部边界点的聚拢趋势信息获取顶点法向量的修正向量,修正后的法向量包含了局部聚拢信息,快速地修补趋于发散的大面积孔洞。

(2)本文算法结合了原插入向量和局部Taubin曲率建立权函数,通过极坐标转换获取权函数值最小时的新增点空间坐标。新增的面片与原始边界面片过渡平滑,且网格大小均匀,形状规则。

(3)本文在VS2013开发环境下开发了网格修复软件,完成了对人体扫描模型的快速修复。算法具有较高的效率和鲁棒性,无论对人为操作形成的孔洞还是扫描信息缺失形成的孔洞都有较好的修复效果。为快速修补扫描模型中大面积缺失以及趋于发散的孔洞提供了一种思路。对人体扫描模型修复、3D反求、个性定制等都具有重要意义。