用反相器实现积分的低压低功耗级联型ΔΣ调制器

李吉军, 张瑞智, 孙权, 张鸿

(西安交通大学微电子学院, 710049, 西安)

模数转换器(ADC)作为模拟信号与数字系统间的桥梁,其精度通常决定了所在电子系统的性能[1]。ΔΣ ADC利用过采样和噪声整形实现极高的转换精度[2],在传感器接口、信号测量、无线通信和生物医疗等方面均有广泛的应用[3]。通常,ΔΣ ADC对元件的匹配度要求远低于其他奈奎斯特ADC[4],适用于互补型金属氧化物半导体(CMOS)工艺[5]。

ΔΣ ADC由ΔΣ调制器和一个数字抽取滤波器组成[6],为了提高ADC的转换精度,传统级联型结构将多个低阶调制器级联起来,再加入数字抵消逻辑,既具有高阶整形效果,又能保证系统的稳定性[7]。该结构中模拟域与数字域传输函数间的失配会导致量化噪声泄漏和调制器精度下降,需要用增益很高的运算放大器(OTA)实现积分,以保证传递函数的精确性[8]。然而,采用高增益OTA会增加调制器整体功耗和硬件开销[9]。带有部分级间反馈的级联结构,可以仅在模拟域构造信号和噪声传递函数,大大降低了对电路的匹配性和OTA增益的要求[10]。

为了进一步降低调制器电源电压和功耗,本文在带有级间反馈的级联结构基础上,采用低增益C类反相器替代OTA实现了伪差分自校准积分器,大大降低了电路的工作电压和功耗。另外,本文还对放大器有限增益对调制器的影响进行了详细的数学分析,为调制器设计提供了理论依据。调制器采用0.5 μm CMOS工艺设计,仿真结果表明,调制器可以工作在1.4 V的低电源电压下,并以极低的功耗实现近100 dB的信噪失真比(SNDR)。

1 OTA增益对量化噪声的影响分析

OTA增益决定了模拟积分器精度,进而影响调制器中量化噪声的整形效果。本章分别对传统级联结构和带级间反馈的级联结构中OTA增益的影响进行分析和对比,为调制器设计提供理论依据。

1.1 传统级联结构

典型的级联结构调制器包含由积分器构成的滤波环路、量化器和数字抵消逻辑[11]。以两级级联的调制器为例,输入信号X经过第1级调制器的信号传递函数HSTF1处理,通过量化器Q1产生第1级的数字输出Y1,其量化噪声E1被噪声传递函数HNTF1整形;第2级调制器以E1为输入,处理过程与第1级相似,并得到输出Y2;两级的输出结果Y1和Y2再经过数字抵消逻辑处理得到最终结果Y,如图1所示。

HSTF1、HSTF2:信号传递函数; HNTF1、HNTF2:噪声传递函数;Q1、Q2:量化器; HD1、HD2:数字抵消逻辑的传递函数; E1、E2:量化噪声; Y1、Y2:数字输出码; X、Y:调制器的输入和输出图1 传统两级级联调制器

经过推导,调制器输出Y可以表示为

Y=HD1Y1+HD2Y2=HD1HSTF1X+

(HD1HNTF1-HD2HSTF2)E1-HD2HNTF2E2

(1)

如果调制器传递函数与HD1和HD2存在以下关系

则有

Y=HSTF1HSTF2X-HNTF1HNTF2E2

(3)

即E1被完全消除,仅有经过高阶整形的E2出现在调制器输出中。通常,信号传递函数仅对输入信号产生几个周期的延时,而量化噪声则经过Li阶整形。因此,将两级的信号传递函数和噪声传递函数分别选择为

式中:Li为第i级调制器的阶数。代入式(3)得到最终输出

Y=z-LiX-(1-z-1)LiE2

(5)

基于白噪声假设和z=ej2πf/fs的基本z变换公式,对于Li阶理想级联型调制器,信号带内量化噪声功率(PIBN)为[12]

式中:M表示过采样率。式(6)是一个通用表达式,不针对特定结构,因此没有出现调制器系数和量化器增益。为了衡量积分器中OTA有限增益的影响,需要计算放大器输出电压与其增益的关系,借助图2中考虑OTA有限增益的开关电容模型,可以得到积分器第n个周期的输出电压

Vi1～Vin:输入电压; Vo:输出电压; CSi、CI、CP:采样电容、积分电容、寄生电容; Ф1、Ф2:两相不交叠时钟; A:OTA增益图2 考虑OTA有限增益的开关电容积分器模型

对式(7)进行z变换,可以得到积分器输入电压与输出电压在z域的关系

Vo(z)=

式中

式(8)表明,OTA的有限直流增益将使积分器出现增益误差和相位误差。不考虑具体积分系数,即令

得到积分器传递函数HITF(z)的表达式

则调制器的信号传递函数和噪声传递函数为

式(12)表明,OTA有限增益将导致E1泄漏至输出端,严重影响调制器整体性能。根据式(8),可将调制器带内量化噪声功率重新计算为

式中:L1和L2分别为两级调制器的阶数,且L1+L2=L。可以看到,量化噪声同时受到M和A的影响。为了使实际量化噪声功率接近式(6)的理想情况,即将其抑制到1/M2L+1的数量级,第1级调制器OTA的直流增益至少需要达到ML+1,第2级调制器OTA的直流增益与M数量级一致即可。这一结果证明了传统级联结构需要高增益放大器来抑制模拟域传递函数与数字域传递函数失配引起的量化噪声泄漏。

1.2 带级间反馈的级联结构

在传统级联结构中引入部分级间反馈,即将第2级调制器的输出反馈到第1级调制器的环路中,能克服传统级联结构的缺点,并可去除数字抵消逻辑,如图3所示。调制器整体输出结果为

Y=HSTF1X-HNTF1HNTF2E2+HNTF1(1-HSTF2)E1

(14)

对比式(14)与式(3)可知,带有级间反馈的级联结构的输出中多了一个与E1有关的项HNTF1(1-HSTF2)E1。令HSTF2=1,可将E1完全消除。考虑到实际电路中实现无延迟传递函数的难度,重新选择HNTF2=1-HSTF2,则得到输出结果

Y=HSTF1X-HNTF1HNTF2E2+HNTF1HNTF2E1=

z-L1-(1-z-1)L1+L2E2+(1-z-1)L1+L2E1

(15)

输出中包含延时的输入信号和经过同样高阶整形的两级调制器量化噪声。其带内量化噪声功率为

式(16)表明,两级调制器贡献的量化噪声相同[10]。考虑OTA有限直流增益的影响后量化噪声功率为

式(17)表明,只需要调制器中OTA增益大致与M在同一数量级,即可将量化噪声功率抑制到接近式(16)给出的理想情况。

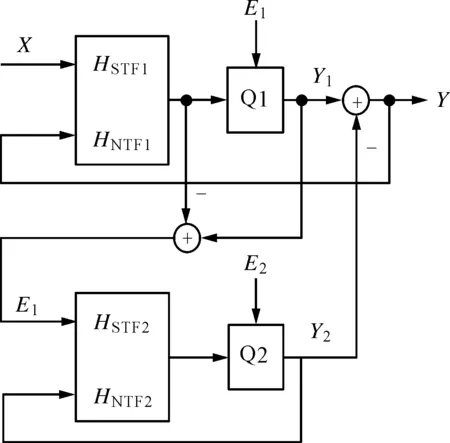
图3 带级间反馈的两级级联调制器

为了验证上述分析,分别对2种结构进行了建模和仿真。2种结构采用相同的参数(L1=2,L2=2,L=4),过采样率都为128。仿真结果表明,级间反馈结构大致需要40 dB的直流增益即可获得大于100 dB的信噪失真比,而传统级联结构需要80 dB以上的直流增益才能使信噪失真比达到相同的水平,如图4所示。

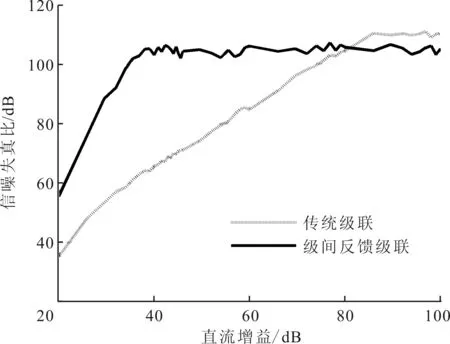
图4 2种级联结构的增益要求

2 调制器电路设计

级间反馈结构降低了积分器中放大器的增益要求,本文中的2级(4阶)级联调制器采用反相器实现积分功能,包括分别由4个反相器构成的伪差分积分器、2个单比特量化器(Q1、Q2)、数模转换器(DAC)和时钟电路,其整体结构如图5所示。其中,a1～a4为调制器系数。

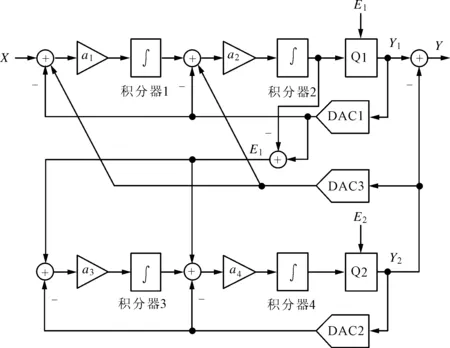
图5 用反相器实现积分的级联型调制器结构

2.1 采用反相器的自校准积分器

基于反相器的积分器是本文调制器的核心模块。为了降低调制器的电源电压和整体功耗,采用C类反相器替代OTA构造积分器,并在采样时钟Φ1和积分时钟Φ2控制下工作,如图6所示。DAC模块可以借助积分器的开关电容网络实现信号反馈。

CS、CI、CC、CM:采样电容、积分电容、补偿电容、共模检测电容;Vip、Vin:差动输入电压的正、负极; Vop、Von:差动输出电压的正、负极; VCM:共模电压; VG+、VG-:虚地点电压; VX+、VX-:反相器输入端电压; VOFF:失调电压; VCI:积分电容两侧电压图6 采用反相器的伪差分自校准积分器

反相器不能提供类似OTA中的虚地,在形成闭环回路时,其输入端存在失调电压VOFF,其计算公式如下

失调电压VOFF会导致CS转移到CI的电荷量出现误差,影响积分精度和调制器性能,因此需要校准。本文的伪差分结构积分器可实现失调电压的自校准。本文采用0.5 μm CMOS工艺,NMOS和PMOS的阈值电压分别为VTHN=724 mV和VTHP=-712 mV,选择电源电压VDD=VTHN+|VTHP|,即1.4 V时,推挽互补结构的CMOS反相器偏置在强反型区与弱反型区边界,可以获得较优的直流增益和增益带宽积折中,反相器作为AB类运放工作[13]。以伪差分结构的正端为例分析:在Φ1时钟相,采样电容CS对输入电压采样,补偿电容CC对失调电压VOFF采样,共模检测电容CM上的电荷完全泄放,VX大致在共模电压(0.7 V)附近,N型晶体管(NMOS)和P型晶体管(PMOS)偏置在亚阈值区边界,静态功耗很小。Φ2时钟相的起始时刻,CS下极板接地,VX+跳变至VOFF-Vip,反相器中一只晶体管进入强反型区,另一只完全截止,Φ2时钟相内,CS上的电荷开始转移至CI,VX逐渐回到VOFF,反相器回到亚阈值偏置状态;电荷转移过程结束后,由于反相器仍然处于闭环状态,其输入端失调电压保持为VOFF,而CC没有电荷泄放通路,储存在该CC上的电荷不变,加在CC两端的电压VOFF也不变,这会强制VG成为“信号地”,CS上的电荷完全转移至积分电容CI;同时,CM对Vop和Von采样,并将开关电容电路的运算结果输出至VG,完成共模反馈。

实际积分器电路中采用共源共栅结构的C类反相器,即在基本反相器MN1和MP1的基础上增加一对共源共栅管MN2和MP2,以保证反相器增益达到40 dB,如图7所示。

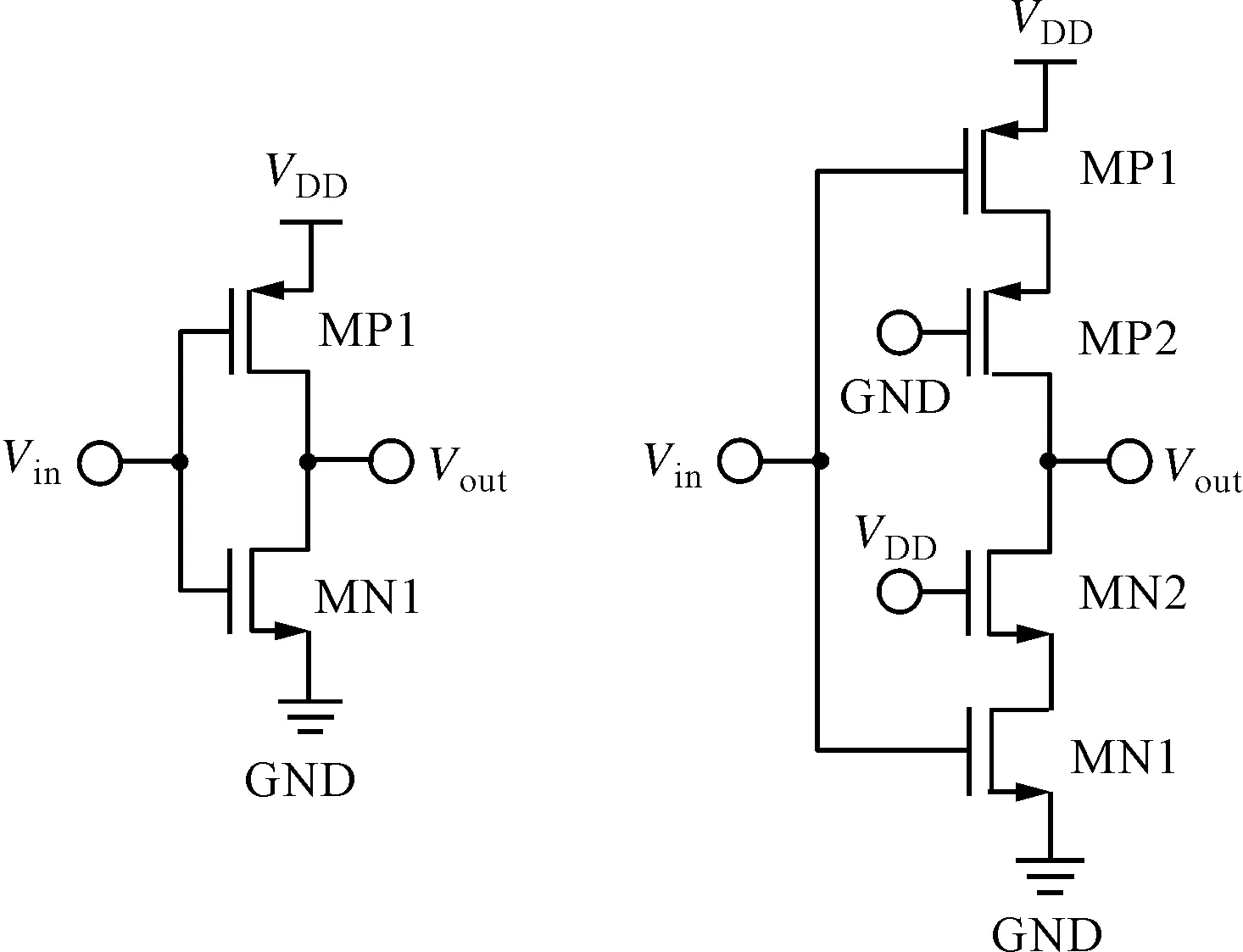
(a)基本反相器 (b)共源共栅结构反相器VDD、GND:电源电压和电源地图7 基本反相器与共源共栅结构反相器

2.2 时钟电路

积分器需要在两相不交叠时钟控制下工作,由于电源电压较低,需要使用时钟自举电路将时钟抬高,以保证CMOS开关充分导通,减少导通电阻对电路的影响[14]。

本文采用的时钟自举电路如图8所示,低电压域的两相不交叠时钟a1和a2控制自举电路,将C1和C2上极板电压抬高一个VDD,输出高电压域的两相不交叠时钟Φ1和Φ2。需要注意的是,MP5和MP7的源端电压高于VDD,其衬底要接自身源端才能正常工作。

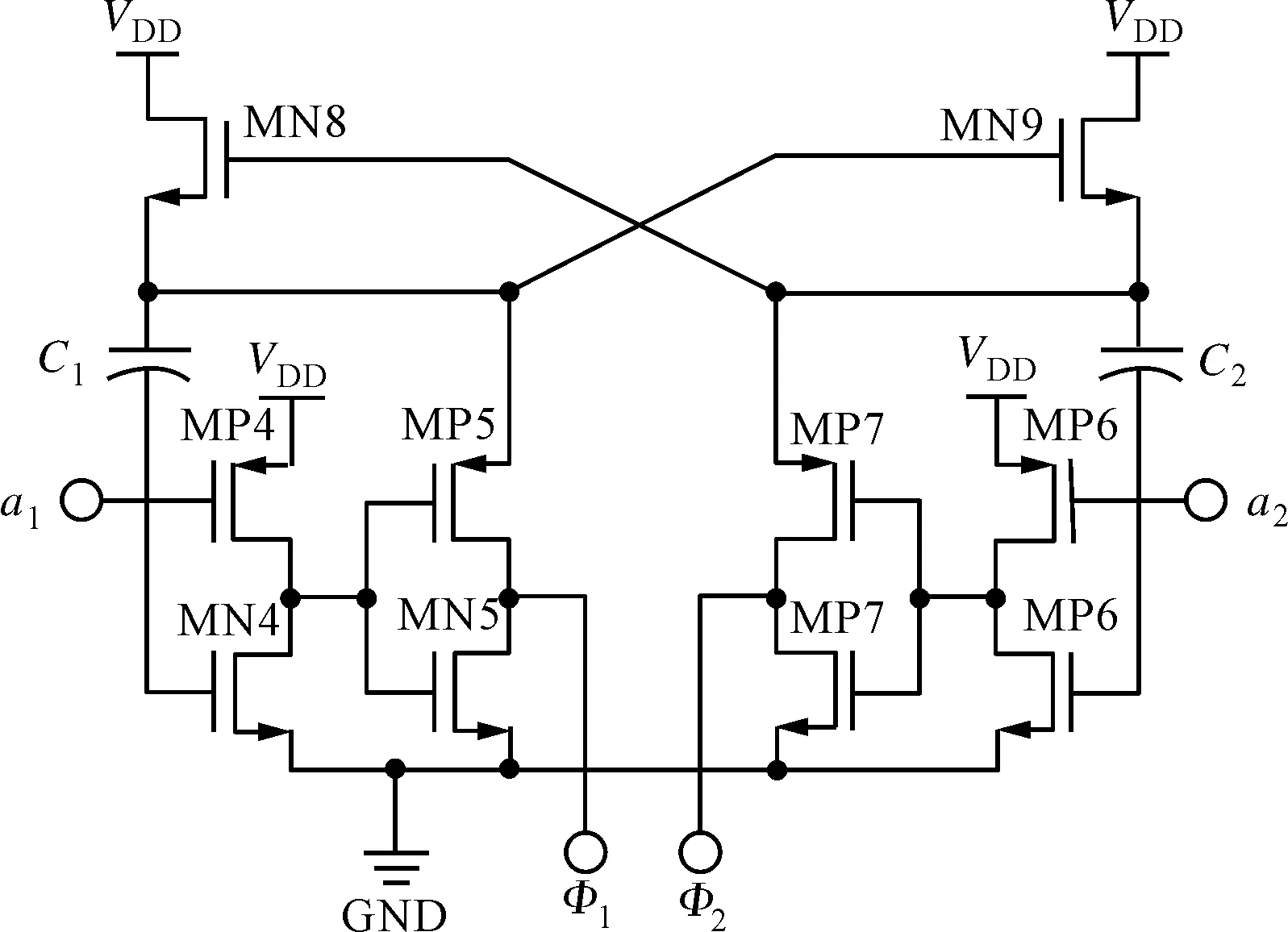
MN4～MN9:NMOS晶体管; MP4～MP7:PMOS晶体管;C1、C2:自举电容; a1、a2:低压域两相不交叠时钟;Ф1、Ф2:高电压域两相不交叠时钟图8 本文采用的时钟自举电路

3 仿真结果

本文的调制器采用0.5 μm CMOS工艺设计,由于采用反相器实现积分功能,电源电压低于1.4 V时,SNDR才出现较为显著的恶化,如图9所示。调制器的版图核心面积858 μm×525 μm,如图10所示。

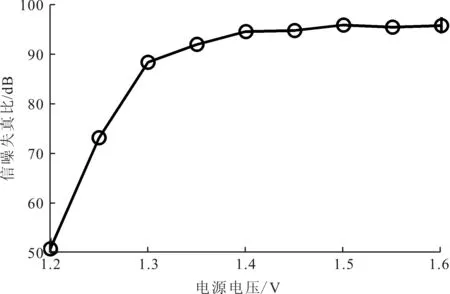
图9 不同电源电压下调制器的信噪失真比

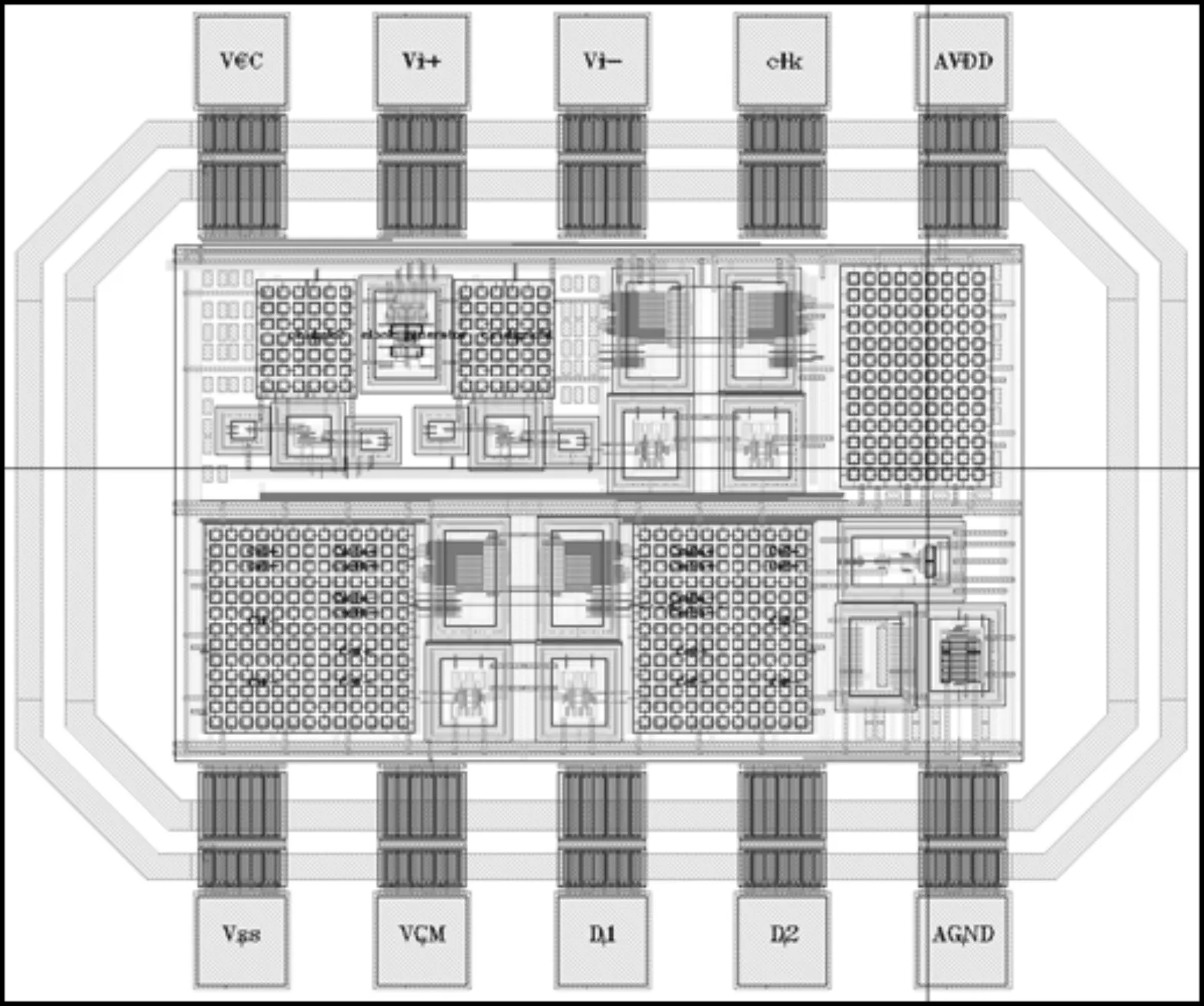
图10 调制器版图

采用Spectre对电路进行仿真,调制器将输入正弦信号的幅值信息调制成为2串数字码流D1和D2。采样频率为1 MHz,输入信号频率为1 037.597 656 25 Hz时,对D1和D2处理并进行FFT分析,得到调制器的输出频谱,如图11所示。

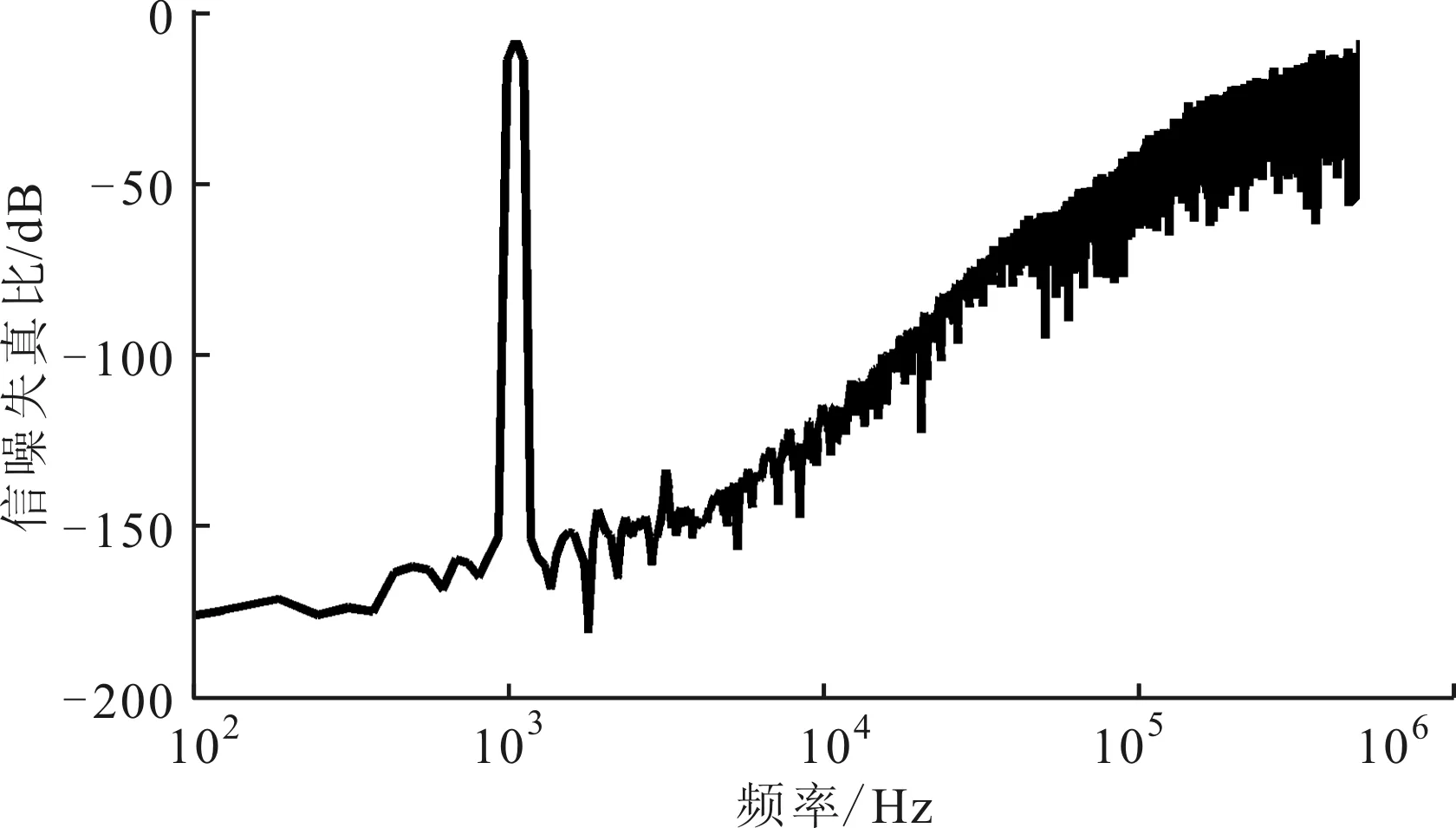
图11 调制器动态性能仿真结果

典型(tt)工艺角下,调制器信噪失真比峰值达到99.8 dB,有效位数16.29 bit;慢速(ss)、快速(ff)、NMOS慢PMOS快(sf)、NMOS快PMOS慢(fs)工艺角下,信噪失真比峰值分布范围为95.1～98.3 dB,其中ss工艺角为最差情况,偏离tt工艺角3.7 dB。仿真结果表明,本文的调制器结构在不同工艺角下SNDR曲线偏差不大,仿真结果受工艺波动影响较小,具有较好的工艺鲁棒性,不同工艺角下调制器SNDR随输入信号幅度的变化如图12所示。

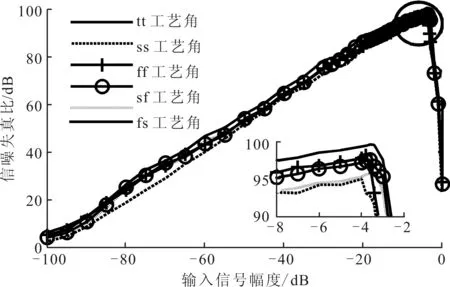
图12 不同工艺角调制器信噪失真比随输入信号幅度的变化

调制器平均电流消耗58.6 μA,其性能采用综合优值(FOM)衡量[13]

式中:D表示调制器动态范围;B表示调制器信号带宽;P表示调制器功耗。

表1总结了调制器的详细性能参数,并与近期相关文献进行了对比。可以看出,本文调制器的精度优势明显。另外,虽然本文采用的工艺相对落后,但由于采用了反相器实现积分功能,电源电压较低,与其他采用先进工艺的调制器相当,因此FOM具有一定优势。

表1 4种不同结构调制器的性能总结与对比

4 总 结

本文设计了一种对放大器增益不敏感的级联型低压低功耗调制器,并采用C类反相器替代OTA实现积分功能,显著降低了电源电压和功耗。电路采用0.5 μm CMOS工艺设计。仿真结果表明,调制器的有效位数达到16位,平均电流消耗为58.6 μA,版图核心面积为858 μm×525 μm,FOM为177 dB。