“分式单元起始课”教学设计与思考

■王 华

发展数学核心素养，是数学课堂教学的重要育人任务。经历发展数学核心素养所需要的数学活动，是有效途径。在具体的单元起始课教学中，设计合理的活动，让学生经历分式概念、分式基本性质、分式运算和分式方程的抽象过程，构建分式这一章的研究思路，探寻研究方法，对于发展学生数学抽象和逻辑推理素养，具有重要的教学实践意义。下面以“分式单元起始课教学为例，研究在教学过程中怎样实现发展数学抽象和逻辑推理素养的育人价值。

一、教学内容

分式整章建构，引导学生了解“为什么要学”“将要学什么”“如何学分式”。

二、教学目标

经历从实际问题中抽象出分式概念、分式的基本性质、分式的运算和分式方程的过程，构建分式这一章的研究思路，探寻研究的方法。

三、教学过程

1.基于情境，以分数“长”分式。

问题1：如图1，已知长方形的面积和其中一边的长，求另一边的长。

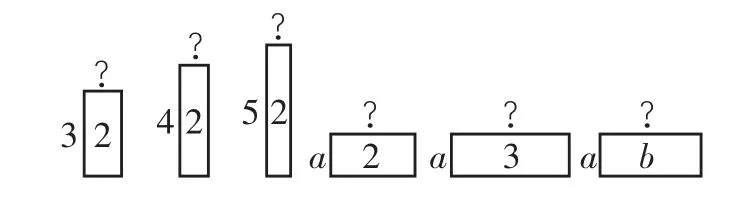
图1

问题2：京沪铁路是我国东部沿海地区纵贯南北的交通大动脉，全长1462km，是我国最繁忙的铁路干线之一。

如果货车的速度是90km/h，客车的速度是货车的2倍，那么：（1）货车从北京到上海需要多少时间？（2）客车从北京到上海需要多少时间？

如果货车的速度是a km/h，客车的速度是货车的2倍，那么：（1）货车从北京到上海需要多少时间？（2）客车从北京到上海需要多少时间？（3）若经过技术升级，货车提速10km/h，则该货车从北京到上海需要多少时间？

设计意图：以长方形面积、火车行驶问题为背景，分别从数学现实和生活现实两个角度，引导学生经历从分数到分式的类比过程，抽象出“新的代数式”，从而感受研究分式的必要性。

2.提炼共性，关注概念形成。

设计意图：将新的式子与分数加以比较。（1）引导学生从形式上发现相同点，即都有分数线，本质上都是除法运算的结果。（2）引导学生分别从分子、分母上找不同点，即分数的分子都是整数，新代数式的分子可以是整数，也可以含有字母；从分母上来看，分数是整数，新代数式的分母含有字母。进而概括分式的本质属性（共同特征）并加以命名（没有必要精致化概念，只通过本质属性的提炼而命名分式）。此时，师生共同归纳：研究定义就是要通过实例来提炼一类数学对象的共同特征。

设计意图：让学生感受分式存在于很多实际问题之中，同一个分式有不同的实际意义。

设计意图：结合学生举的实例，明确用具体的数值代替分式中的字母，就能得到相应的分式的值。当分式中的字母取定后，分式的值可以为某些分数，通过这一环节，学生体会分式与分数不仅形式相同，而且还存在其他的数学联系。进一步地，通过追问的设计，明晰研究分式概念、分式的值和取值范围的必要性。

3.拼接矩形，感悟分式性质。

问题6：按要求拼一拼，想一想。

材料：全等的长方形纸片若干张。操作方法：（1）如图2，1张长方形纸片的面积为b，一边长为a，则另一边长为多少？（2）如图3，2张长方形纸片的面积为2b，一边长为2a，则另一边长为多少？（3）如图4，3张长方形纸片的面积为3b，一边长为3a，则另一边长为多少？（4）n张长方形纸片的面积为nb，一边长为na，则另一边长为多少？（5）你发现了什么？

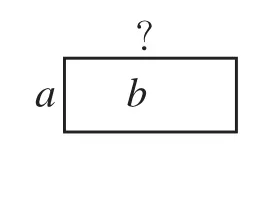
图2

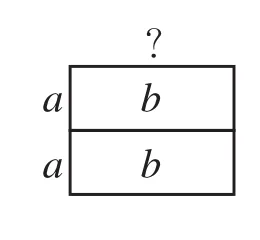
图3

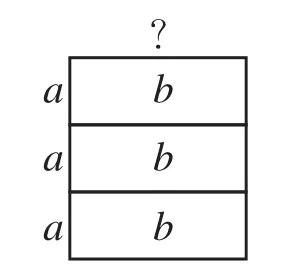
图4

隐喻：“乒乓球和网球”的故事。乒乓球与网球是两种球类运动，在形式上有很多相似之处：都是单人或者双人进行比赛；比赛场地都是用网相隔；规定球都要直接打到对方的区域。于是就可以从乒乓球比赛“交换发球”这个规则，跳跃地联想到网球比赛的规则中也可能有“交换发球”。

设计意图：长方形纸片的增加，导致整体面积扩大，一边长随之扩大，而另一边长始终不变，引导学生得出即分式的分子、分母同时乘或除以同一个数，分式的值不变。此时，回想分数的基本性质，发现分式不仅与分数形式相同，而且还有与分数相类似的性质。在此基础上追问：这意味着什么？再通过“乒乓球和网球”的故事加以隐喻，从而明确我们可以大胆参照分数去学习分式其他各部分的知识。师生共同归纳：研究分式性质，就是联系分数的基本性质，研究分式值的不变性。

4.类比分数，把握分式运算。

问题7：京沪铁路是我国东部沿海地区纵贯南北的交通大动脉，全长1462km，是我国最繁忙的铁路干线之一。如果货车的速度是a km/h，客车速度是货车的2倍，那么：

（1）都驶完全程，哪一辆车用时多？多多少小时？

（2）若经过技术升级，现在货车速度为(a+10)km/h，则货车原来用时是现在的几倍？

设计意图：学生通过对问题情境中两种车辆行驶时间多少、关系的比较，自然地联系分式的减法运算。参照分数的四则运算，学生不仅要学习分式的减法，还要学习分式的加法、乘法、除法以及乘方运算，此时可抽象出分式的除法运算。教师进而追问：分式如何进行运算，能否用一句话概括？联系“乒乓球和网球”的隐喻，学生自然得出：分式的运算参照分数的运算。在此基础上，师生共同归纳：研究分式运算需参照分数的运算（如通分、约分、运算法则等）。

5.回到实际，初识分式方程。

问题8：京沪铁路是我国东部沿海地区纵贯南北的交通大动脉，全长1462km，是我国最繁忙的铁路干线之一。如果货车的速度是a km/h，客车的速度是货车的2倍，那么已知从北京到上海的货车比客车多用6h，求货车的速度。

设计意图：分式方程是分式与分式或分式与整式之间建立的等量关系。在此，教师应关注学生对实际问题中相等关系的把握，引导学生尝试建构，并初步感受转化为整式方程是解决此类方程的关键所在。在方程的解决过程中教师有必要提出今后研究的方向，如分式方程转化为整式方程后，有没有问题？有什么问题？师生共同归纳：分式问题转化为整式问题。

6.构建框图，升华研究过程。

师：本节课我们通过一系列问题，研究了分式的概念→分式的性质→分式的运算→分式方程，现在有必要再次梳理它们的关系，框图。

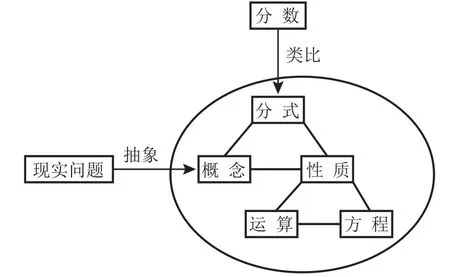
问题9：我们是按照什么样的思路研究分式这一章的知识的？研究的方法是什么？

设计意图：回顾本节课的探究过程，梳理研究思路，帮助学生在脑海中形成分式这一章的学习框图。

师：从知识方面讲，我们搭建了从分式概念、性质、运算、方程的学习框图，而这些都是我们用数学的眼光从现实问题中抽象出来的。那我们是如何研究的呢？一开始，在对概念的学习中，我们发现分式与分数只是形式相同，隐隐约约感觉有一点数学联系，经过对性质的探究，发现分式与分数不仅形式相同，而且性质也是类似的。故大胆推测分式在其他方面也是与分数类似的，这种方法在数学上称为类比。

四、教学反思

1.让学生经历抽象出分式概念、基本性质、运算和方程的过程。

从“长方形面积”“火车行驶”两个问题情境出发，让学生经历表示分式的抽象活动，发现一类新的代数式，从而体会从分数到分式的类比过程。而后基于“长方形面积”问题，设计“等宽长方形”操作，让学生体会分式值的不变性，从而抽象出分式的基本性质；基于“火车行驶”问题，分别抽象出分式的运算和分式方程，并在学习分数的基础上获得研究的方法。学生通过这样的设计，感受分式大量存在于现实生活当中，从而体会研究分式的必要性，即明白“为什么要学”。而利用两个问题情境将分式的知识框架串通，又能让学生明确分式的研究思路，即了解“将要学什么”。

2.让学生经历从分数到分式的类比过程，获得“如何学”的方法。

学习概念时，学生发现分式与分数只是形式相同，并有一定的数学联系，而后经过性质的探究，发现分式与分数不仅形式相同，而且性质也是类似的，从而得到了类比的前提条件，即类与类之间有很多的相同属性，故大胆推测分式在其他方面也是与分数类似的。上述类比过程自始至终贯穿整节课，是一条指引学生“如何学”的主线，“授人以鱼”的同时“授人以渔”。学生在了解分式研究方法的同时，也学会了如何用类比的方法获得新的知识。

3.基于章节起始课教学，关注学生数学核心素养的落实。

本节课用现实问题贯穿整个分式章节，关注数学抽象素养的落实。另外，由分数到分式的类比学习，体现了类与类之间归纳推理，关注了逻辑推理的落实。通过让学生举例子来说明的实际意义等环节的设计，关注了数学建模的落实。在分式的加减运算、分式方程的求解环节，师生共同探究解决问题的方法，又落实了数学运算这一核心素养。至此，数学章节起始课的育人功能水到渠成。