一类特殊的二阶常系数线性非齐次微分方程的解法
2018-08-11朱立明
周 恺,高 芳,朱立明
(池州学院 数学与计算机学院,安徽 池州 247100)
常系数线性非齐次微分方程是高等数学教学中的一个重要内容,许多文献都讨论了其求解问题[1-4].根据线性微分方程解的结构,求解问题转化为求对应齐次方程的通解和非齐次方程的特解.一般教材中都利用待定系数法求方程的特解.笔者在教学过程中发现,学生利用待定系数法求特解时,经常会出现计算错误.因此,本文给出一类特定形式下二阶常系数线性非齐次微分方程特解的巧妙计算.
对于微分方程

当 f(x)=eλxP1(x)时,其中 λ∈R,P1(x)=rx+s我们分三种情形给出相应结论.
(1)当 λ2+pλ+q≠0 时,可设特解 y*=eλx(ax+b),则

将 y*",y*',y*代入(1)中,整理可得

比较系数,可知

此时,待求特解表达式中的未知系数可由P1(x)的系数和p,q,λ唯一确定,这样可以省去中间的求导计算.下面我们给出一个教材中的例子,通过两种方法的计算,说明上面结论在具体计算中的简洁性.
例1[5]求微分方程y"-2y'-3y=3x+1的通解.
原方程对应的齐次方程为
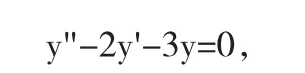
它的特征方程
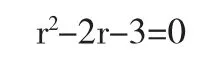
有两个实根r1=-1,r2=3,
于是与所给方程对应的齐次方程的通解为

下面求非齐次方程的特解.
解法1 由于f(x)=3x+1,所以可设特解y*=ax+b,带入原方程得到
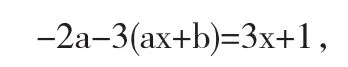
比较两边系数得到,

解法 2 设特解y*=ax+b,由于 r=3,s=1,λ=0,p=-2,q=-3,利用(2)(3)两式可得,因此特解也为
(2)当 λ2+pλ+q=0,2λ+p≠0 时,可设特解 y*=eλxx(ax+b),则

将 y*",y*',y*代入(1)中,整理可得
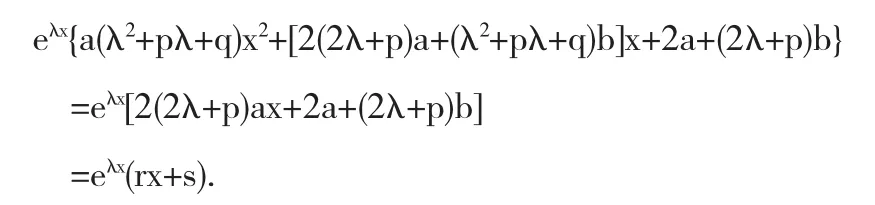
比较系数,可知

例2[5]求微分方程y"-5y'+6y=xe2x的通解.
原方程对应的齐次方程为

它的特征方程

有两个实根r1=2,r2=3,
于是与所给方程对应的齐次方程的通解为

下面求非齐次方程的特解.
解法1 由于f(x)=xe2x,所以可设特解y*=x(ax+b)e2x,则

代入原方程得到

比较两边系数得到,

解法2 设特解y*=x(ax+b)e2x,由于r=1,s=0,λ=2,p=-5,q=6,利用(4)(5)两式可得
(3)当 λ2+pλ+q=0,2λ+p=0 时,可设特解 y*=eλxx2(ax+b),则

将 y*",y*',y*代入(1)中,整理可得
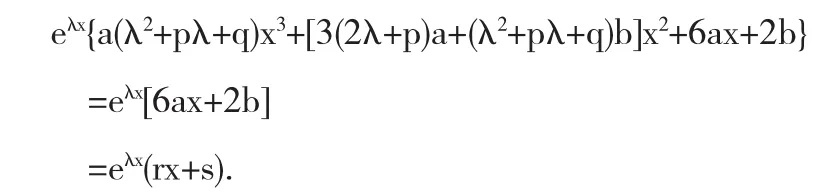
比较系数,可知

注:特别地在 s=0,即 f1(x)=rxeλx,当 λ 是(1)对应的齐次方程特征方程的二重特征根时,b=0.因此,可以设特解y*=eλxx2·ax.由于不含有常数项,可以简化特解y*的求导,从而使得计算过程变得简单.笔者查阅了大部分高校选用的高等数学[5]及常微分方程[7]教材,都没有明确指出这一点.
下面我们举一例加以说明.
例3[6]求微分方程y"+6y'+9y=6xe-3x的通解.
原方程对应的齐次方程为

它的特征方程

有实根r1=r2=-3,
于是与所给方程对应的齐次方程的通解为
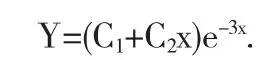
在教材[6]中,设特解为 y*=x2(ax+b)e-3x.由于 f(x)=6xe-3x,根据上面的注记,可设特解y*=ax3e-3x,则y*'=(-3ax3+3ax2)e-3x,y*"=(9ax3-18ax2+6ax)e-3x,
代入原方程得
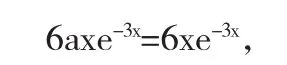
所以a=1,y*=x3e-3x,故原方程的特解为

