基于自适应步长的改进布谷鸟算法

孙 敏，房明磊，韦 慧

（安徽理工大学 数学与大数据学院，安徽 淮南 232001）

近年来，各种启发式算法不断涌现，如遗传算法[1]，粒子群算法[2]等，它们都是通过模拟生物的行为或自然界的现象来解决最优化问题.随着模拟生物行为的不断发展，2009年，剑桥大学的Yang和Deb通过模拟布谷鸟寻窝产卵的行为提出了一种新的搜索算法，即布谷鸟搜索算法（Cuckoo Search，CS)[3].由于这种算法简单高效、参数少、易于实现、随机搜索路径优等特点，已成功应用于工程设计优化[4]、多目标优化[5]、人脸识别[6]、神经网络训练[7]、整数规划[8]和多阈值图像分割[9]等实际问题中.

但CS算法与其他一些智能算法一样，存在后期精度不高、搜索速度慢等缺点.针对这些不足，Valian等[10]引入自适应机制，提出了一种自适应步长和自适应发现概率的CS算法，提高了原始CS算法的性能.王凡等[11]重点探索了基于高斯扰动的CS算法，在迭代过程中对鸟窝加入高斯扰动，增强了鸟窝位置变化的活力.王李进等[12]提出了一种基于逐维改进的CS算法，改进的算法针对解采用逐维更新评价策略，有效地提高了CS算法的收敛速度并改善解的质量.李明等[13]介绍了一种和差分进化算法结合的混合CS算法，提高了算法的寻优精度.

本文针对CS算法的步长、发现概率和缩放因子引入动态自适应策略，提出了一种基于自适应步长的改进布谷鸟算法（improved Cuckoo Search,iCS），以提高算法的收敛速度和求解精度.

1 基本的布谷鸟搜索算法

自然界中，布谷鸟不仅有令人着迷的美妙声音，而且有独特的繁衍方式.它们是通过寄生育雏的方式来繁殖下一代，将自己产下的卵偷偷放入宿主鸟窝中，让它们为其孵化下一代.为了避免被发现，一些布谷鸟将自己的卵模仿成宿主鸟的卵，由于布谷鸟的卵比宿主鸟孵化的时间早，孵化的雏鸟会本能地将宿主的幼雏或卵推出巢穴，这将会提高它们自己获得宿主食物的可能性，从而增大存活概率.一旦被宿主鸟发现，宿主鸟就会将外来的卵直接丢弃或弃窝另筑新窝.

布谷鸟寻找适合自己产卵的鸟窝位置是随机或类随机的方式，为了模拟布谷鸟寻窝的行为，首先，设定以下3个理想化状态[3]：

（1）每只布谷鸟1次只产1个蛋并随机选择鸟窝来放置它.

（2）最好的鸟窝（解）将被保留到下一代.

（3）可利用的鸟窝数量n是固定的,宿主鸟能发现外来鸟蛋的概率pa∈[0,1].

在这种情况下，宿主鸟可将该鸟蛋丢弃或放弃这个鸟窝，另寻地方再重新建1个新鸟窝.

在这3个理想状态的基础上，布谷鸟按莱维飞行（lêvy flight）方式搜索鸟窝的路径和位置更新公式[3]如式（1）所示：

式中xit和xit+1分别表示第t代和第（t+1）代的位置；⊕为点对点乘法；α表示步长控制因子；lêvy（λ）为lêvy随机搜索路径，并且其与时间t的关系服从 lêvy 分布，即 lêvy（λ）~u=t-λ(1＜λ≤3).

通过位置更新后，用随机数r∈[0,1]与pa对比，若r＞pa，则对xit+1采用偏好随机游动方式进行改变，偏好随机游动如式（2）所示：

式中，r是缩放因子，服从（0,1）区间上的均匀分布，xjt和xkt表示第t代的两个随机解.

2 改进的布谷鸟搜索算法

2.1 改进算法的内容

在基本的CS算法中，随机步长是通过lêvy flight产生的，搜索时，步长时大时小，步长越大越有利于搜索全局最优，但降低了搜索精度，有时会出现震荡现象.若步长越小，则结果相反.因此针对lêvy flight产生的步长虽具有随机性但缺乏自适应性问题，郑洪清等[14]根据不同阶段的搜索结果提出了一种自适应步长布谷鸟搜索算法（Self-Adaptive Step Cuckoo Search algorithm,ASCS）.该算法自适应动态调整了步长的大小，增加了解的多样性，使算法的搜索速度和精度都有较大的提高.其自适应策略如下：

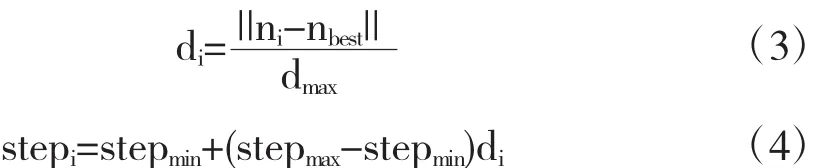
式中，ni表示第i个鸟窝位置，nbest表示此时鸟窝位置的最佳状态，dmax表示最优位置与其余所有鸟窝位置距离的最大值，stepmax和stepmin分别表示步长的上下限.

根据式（3）和式（4）实现自适应动态调整步长.当第i个鸟窝位置越接近最佳位置时，步长越小，当第i个鸟窝位置离最佳位置较远时，步长越大.这样，由上一代迭代的结果来动态更新本次迭代的移动步长，使算法具有更好的自适应性.

然而，自适应步长布谷鸟搜索算法[14]仅仅只对步长进行改进，其发现概率pa取固定值0.25，不利于保持算法的全局和局部随机搜索之间的平衡；同时，该算法中的缩放因子r取[0,1]区间的均匀分布随机数，对较差的个体没有产生较大的变异，不利于新解的生成.所以，若能较好地控制缩放因子r和发现概率，使较差的个体产生较大变异，从而提高算法的求解精度.

为了克服以上问题，本文提出了一种基于自适应步长的改进布谷鸟搜索算法（iCS），即在自适应步长布谷鸟搜索算法（ASCS）的基础上，引入了发现概率和缩放因子自适应动态调整策略[15]，其缩放因子、发现概率分别调整为：

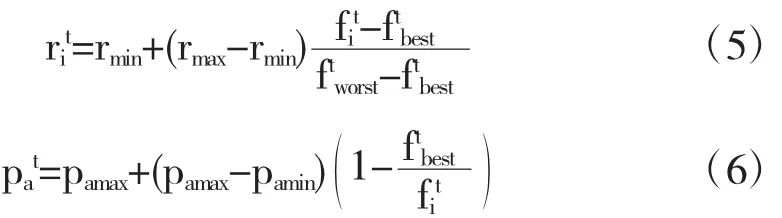
其中，

rit：第t代种群中，第i个个体的缩放因子；

fit、和分别为第 t代种群中第 i个个体、最优个体以及最差个体的适应度；

pat：第t代种群中第i个个体被发现并重新生成新解的概率；

pamax和 pamin：pat的上下限；rmax和 rmin：分别为缩放因子的上下限.

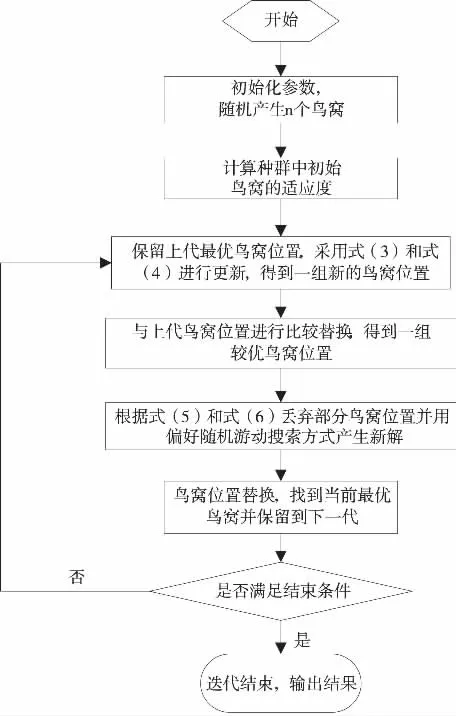
图1 改进算法的流程图

由式（5）和式（6）实现自适应动态调整发现概率和缩放因子，从而使更多的个体参与演化，以提高种群的多样性，避免早熟，达到提高收敛速度和求解精度的目的.

2.2 改进算法的步骤

步骤1 初始化解，随机生成n个鸟窝，搜索空间维数为D,最大迭代次数为itermax，步长step的上下限，发现概率pa和缩放因子r的上下限，并计算所有鸟窝的适应度.

步骤2 保留上代最优鸟窝位置，将其他鸟窝按式（3）和式（4）进行更新，计算更新会后鸟窝的适应度，若新的鸟窝适应度更高，则替换旧的解.

步骤3 通过动态缩放因子（式（5））和动态发现概率（式（6））淘汰部分解，并采用偏好随机游动（式（2））产生与淘汰解数量相同的新解.

步骤4 计算更新的鸟窝适应度，输出当前最优解.

步骤5 判断算法终止条件，若满足则获得结果，否则返回步骤2.

基于以上步骤，改进算法的流程图如图1所示.

3 仿真实验

3.1 实验设计

为验证改进算法的性能，选取如表1所示的4个典型的benchmark函数[12]进行测试.实验中算法参数设置如表2所示，ASCS算法和iCS算法中步长step上下限分别为0.5和0.01.

表1 测试函数

表2 实验参数设置

3.2 实验结果及分析

固定收敛精度tol=1.0e-9，针对不同的标准测试函数，各算法独立运行20次，实验结果如表3所示，表中的最小值、平均值和最大值分别为所运行20次中相应的求得的最小适应值、平均适应值和最大适应值.

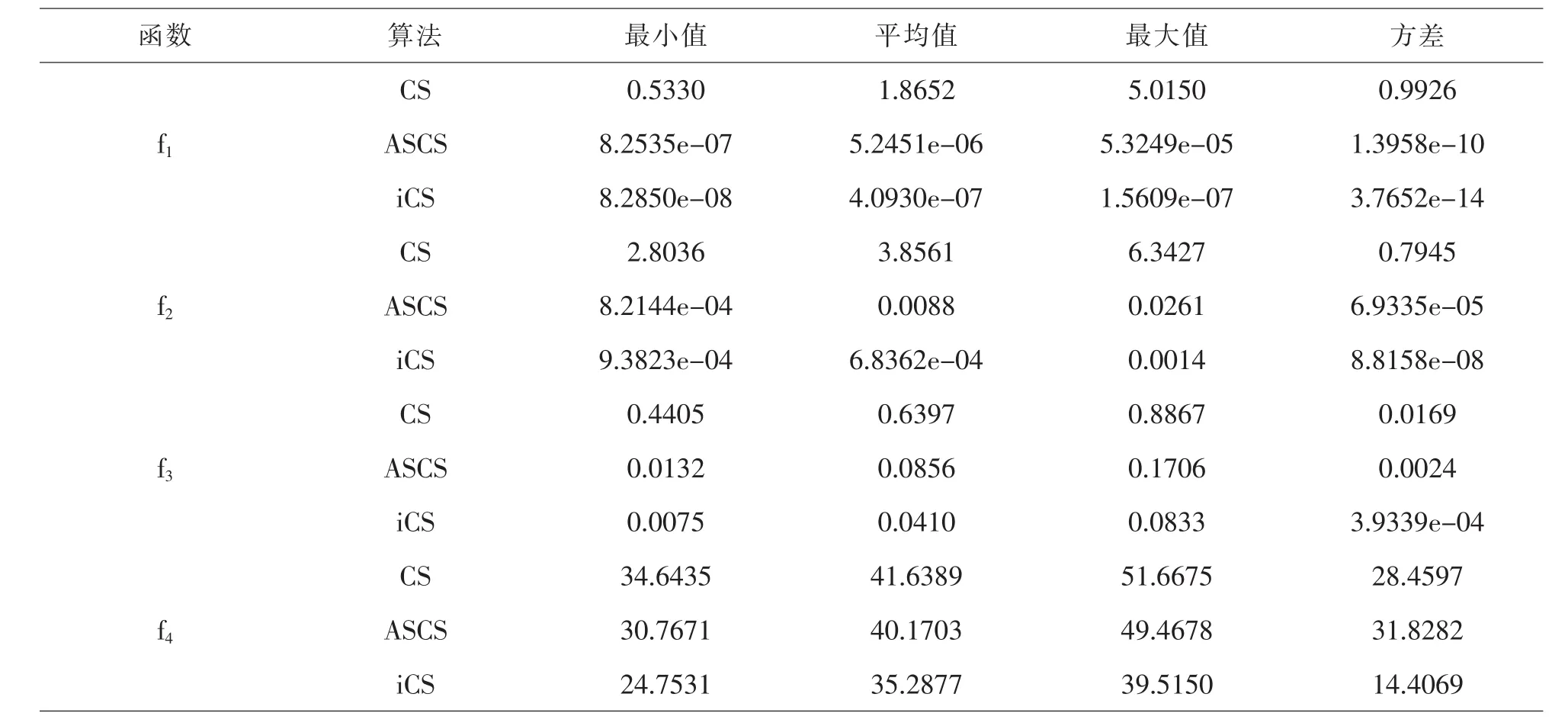
表3 三种优化算法的性能比较

从表3可以看出，对于测试函数f1，iCS算法比CS和ASCS算法的最小值分别提高了7个、1个数量级，平均值也分别提高了7个、1个数量级.对于测试函数f2，iCS算法的最小值比CS算法提高了4个数量级，比ASCS算法提高了1.1679，平均值比CS算法提高了4个数量级，比ASCS算法提高了1个数量级.对于测试函数f3，iCS算法比CS和ASCS算法的最小值分别提高了0.4330、0.0057，平均值分别提高了0.5987、0.0446.对于测试函数f4，iCS算法比CS和ASCS算法的最小值分别提高了9.8904、6.0140，平均值分别提高了6.3512、4.8826.就稳定性而言，iCS算法的稳定性也高于ASCS和CS算法.因此可以得出iCS算法的性能最优，其次是ASCS算法，CS算法最差.

为了反映算法的收敛速度，固定迭代次数为300，每种测试函数独立运行20次.比较三种算法的收敛速度和求解精度.图2—5分别为4个测试函数 f1、f2、f3、f4采用 3 种算法寻优时适应值随迭代次数变化的曲线.

从图2可以看出，对于函数f1，iCS算法迭代150次时最小适应值就已经达到10-2而ASCS算法的适应值较之较大，此时CS算法适应值为102.因此，由图中适应值的变化曲线，可以明显看出iCS收敛速度最快，ASCS次之，CS最慢.当迭代次数都为300次时，iCS算法的精度比ASCS和CS算法好.

从图3可以看出，对于函数f2，iCS算法迭代150次时最小适应值达到10-1，而ASCS算法为100，此时CS算法的最小适应值为101.因此，由迭代过程适应值的变化曲线可知，iCS收敛速度最快，ASCS次之，CS寻优过程适应值下降十分缓慢.当迭代300次后，iCS算法的精度明显比ASCS和CS算法的精度高.

从图4可以看出，对于测试函数f3，iCS算法、ASCS算法寻优时适应值的下降速度也明显比CS快，而iCS的收敛速度略优于ASCS.当迭代300次时，iCS算法的适应值为10-3，比ASCS和CS算法的精度高.

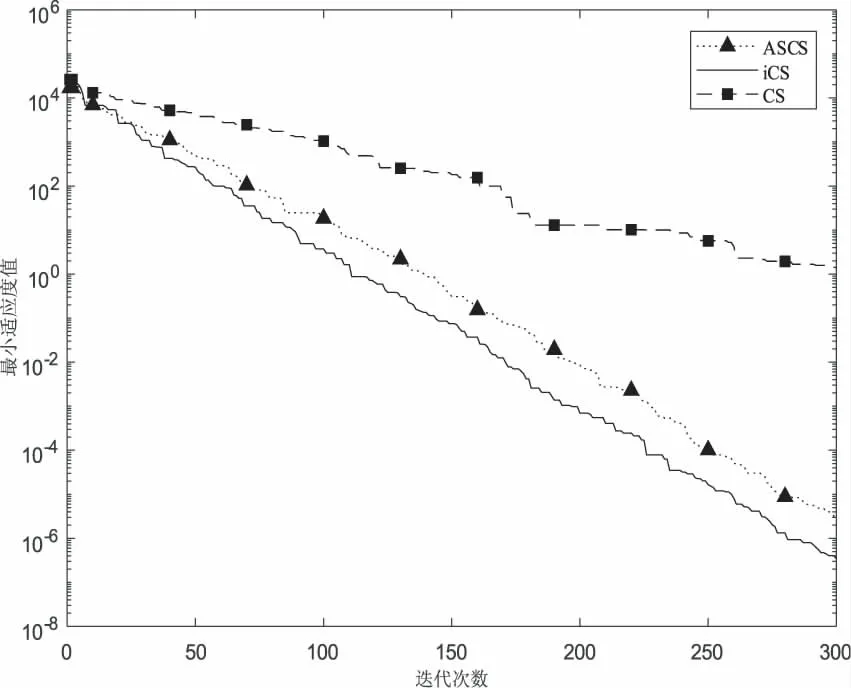
图2 函数f1的收敛曲线

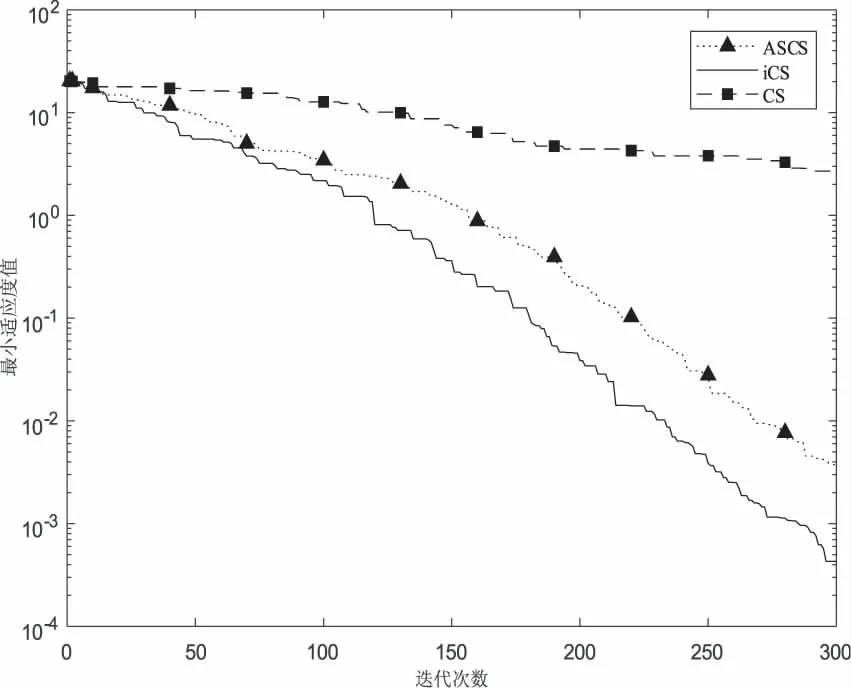
图3 函数f2的收敛曲线

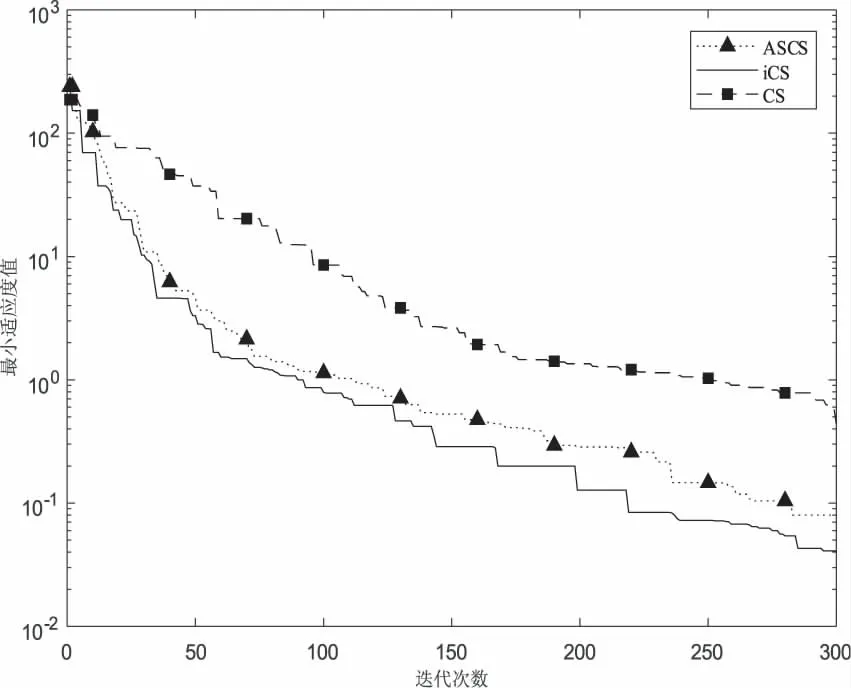
图4 函数f3的收敛曲线

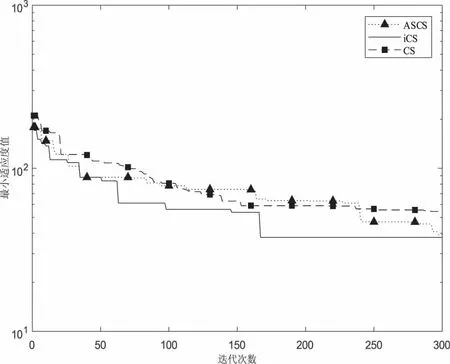
图5 函数f4的收敛曲线

对于测试函数f4，由图5可知，此时，三种算法的收敛速度快慢区别不是很明显，改进的算法略优于ASCS和CS算法.该测试函数是多波谷函数，因此迭代时容易达到局部最优，收敛速度容易受到影响，较前面三种测试函数适应值的下降速度明显变慢.

综上分析可知，引入自适应缩放因子、发现概率的自适应策略，并结合自适应步长的优势，能有效提高CS算法的收敛速度和寻优精度.

4 结语

论文主要引入了针对发现概率和收缩因子的自适应策略对自适应步长布谷鸟算法进行改进.由所给的标准测试函数，讨论了基本CS算法，自适应步长算法和改进算法的收敛速度快慢和精度高低问题.仿真实验结果表明，iCS算法比ASCS算法和CS算法有更佳的寻优性能，能够提高收敛速度和求解精度.然而对于测试函数f4，虽然iCS算法能改善CS算法的性能，但迭代后期易陷入局部最优，这个问题仍然需要进一步研究.