基于Floyd算法对蔬菜运输的研究

陶 涛，朱家明

（1.安徽财经大学 金融学院；2.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030）

为缓解中国副食品供应矛盾，农业部于1988年提出建设“菜篮子工程”.该项目一期工程建立了中央和地方肉类，蛋类，牛奶，水产和蔬菜生产基地以及养殖和饲料加工服务系统，以确保居民全年新鲜供应副食品.作为“菜篮子”工程的产物，蔬菜受到各级政府的重视.到1995年，蔬菜的人均消费量已达到世界平均水平.杭州江干人口近90万.全市在郊区和农业区建立了8个蔬菜种植基地，每天为城市居民提供蔬菜供应任务，并将蔬菜运送到35个蔬菜销售点.市区有15个主要交通枢纽.在运输蔬菜的过程中，蔬菜种植基地可以利用这些交叉路口到达蔬菜销售点.如果蔬菜销售点的需求不能满足，市政府必须对短缺提供一定的补偿.同时，市政府还根据蔬菜种植基地供应蔬菜的数量和距离，提供相应的运费补贴，以增加蔬菜种植的积极性.运费补贴标准为0.04元/（1吨1公里）.对于一些中小城市，蔬菜主要种植在郊区和农业区，通过政府补贴保证城市蔬菜供应.这不仅增加了城市蔬菜供应的数量和质量，也刺激了郊区和农业地区的蔬菜农民的积极性.

1 文献综述

申福军[1]基于总体配送中心选址模型，添加蔬菜农产品配送中心需要考虑的独特约束和独特的目标函数，实现建立蔬菜产品配送中心选址模型的目标.不足之处是假定库存成本没有被考虑在内，但实际上，即使相对时间敏感的蔬菜等农产品在分销系统中也有库存.石钢[2]在前人研究成果的基础上，建立了一个更科学的定量选址模型，不仅考虑了运输和建设成本，新鲜农产品的腐败损失，还考虑到新鲜度问题和经济效益.不足之处是缺乏对大量数据的实证研究和验证.

2 最短运输距离

2.1 研究思路

根据在浙江省统计局所搜集的数据，利用MATLAB绘制出各蔬菜基地、交通路口、销售点之间的连通图，如图1所示.

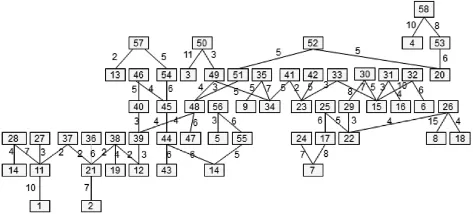
图1 运输路径连通图

由于蔬菜的运输具有无向性，因此我们考虑用Floyd算法求出蔬菜基地到销售点之间的最短距离.

2.2 研究方法

Floyd算法，是一种用于寻找给定加权图中顶点间路径最短的算法，基本步骤如下：

①让所有边加入中间点1，取Aij与Ai1+Aij中较小的值后Aij的新值，完成后得到A(1)；

②让所有边加入中间点2，把Aij与Ai1+Aij中较小的值后 Aij的新值，完成后得到 A(2)，以此类推得到 A(3),A(4),…,A(n)，其中循环到第n个得到的A(n)即我们所求的结果，Aij(n)表示顶点i与j之间的最短距离.

因此可以描述为：（arcsij为临接矩阵）

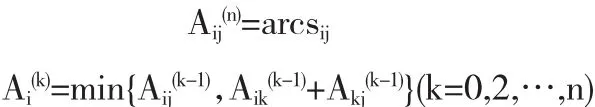
定义一个n阶正矩阵系列：

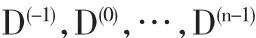
按照以上步骤规定，可以建立58×58的网络权矩阵为：

其中，p=58，Dij为第i个蔬菜种植基地到第j个销售点之间的最短距离.

下面来确定网络权矩阵：

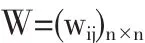
其中，wij=lij，当(vi,vj)属于 E 时，lij为(vi,vj)的权；

因为上述网格有58个结点，故网络的权矩阵均为58阶矩阵.在给出网络最短路线的Floyd算法：

①dl=w(w为所给网络的n阶权矩阵）

②dk=(dkij)n×n，k=2,3,…,p

其中，dkij=min[d(k-1)ij,d(k-1)is+d(k-1)sj]i,j=1,2,…,n

下面来计算次数，当 wij＞0时，p由下式确定：p≥，这样的dp就确定了网络各点间的最短距离.此处

n=15，解出p≥3.3669，故只需取p=4，即算到d4即可.

2.3 结果分析

运用MATLAB软件编程求得8个蔬菜种植基地分别到35个蔬菜销售点之间的最短距离xij，由于数据量较大，故省去部分数据，结果见表1.

表1 基地与销售地之间最短距离一览表

3 无短缺量限制下的最小费用

3.1 研究思路

为了计算无短缺量限制下的最小费用，我们对总生产量与需求量之间的关系进行分析，见表2.

表2 总生产量与需求量对比表

由表2可以看出：蔬菜总生产量小于销售点需求量，该问题属于产量大于销售量，因此可以使用线性规划的方法,求得政府最小补贴费用和最佳运输方案.

3.2 研究方法

总费用包括两部分：蔬菜调运费P各市场供给量小于需求量的短缺损失L，即Z=P+L；根据题意，它们分别可以用公式表示为：

①蔬菜总运输费用P可以表示为：

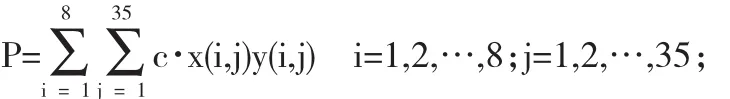
②市场j的短缺量为：

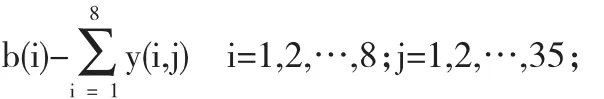
③短缺总补偿L为：

所以最终的目标函数为：

2.3 结果分析

使用LINGO编程求得结果，可知最小政府补贴费用为42833.06元，具体的运输方案为：

①基地1：向销售点4运输14.3吨，向销售点5运输13吨，向销售点13运输8.5吨，向销售点23运输4.2吨.

②基地2：向销售点15运输11.6吨，向销售点17运输13.6吨，向销售点23运输2.5吨，向销售点24运输11.3吨，向销售点25运输6吨.

③基地3：向销售点25运输3.6吨，向销售点27运输7.2吨，向销售点28运输8.9吨，向销售点29运输10.3吨.

④基地4：向销售点11运输5.9吨，向销售点12运输7吨，向销售点24运输1.2吨，向销售点31运输7.7吨，向销售点34运输7.2吨.

⑤基地5：向销售点21运输2.2吨，向销售点22运输7.4吨，向销售点32运输8吨，向销售点33运输11.4吨.

⑥基地6：向销售点10运输7.2吨，向销售点19运输7.3吨，向销售点20运输10吨，向销售点21运输10.5吨.

⑦基地7：向销售点1运输6.5吨，向销售点2运输9吨，向销售点8运输9.5吨.

⑧基地8：向销售点2运输1.2吨，向销售点3运输12吨，向销售点10运输1.2吨，向销售点11运输4.6吨，向销售点18运输9吨.

4 有短缺量限制的最小费用

4.1 研究思路

在无短缺量最小费用模型的基础上，我们加入各蔬菜销售点的短缺量不超过需求量的30%这一新的约束条件得出有短缺量限制的最小费用模型.

4.2 研究方法

4.3 结果分析

使用LINGO编程求得结果，可知最小政府补贴费用为50476.19元，具体的运输方案为：

①基地1：向销售点4运输10.01吨，向销售点5运输9.1吨，向销售点13运输5.95吨，向销售点14运输8.4吨，向销售点15运输6.54吨.

②基地2：向销售点11运输4吨，向销售点15运输1.58吨，向销售点16运输8.75吨，向销售点17运输9.52吨，向销售点23运输6.7吨，向销售点24运输3.95吨，向销售点26运输10.5吨.

③基地3：向销售点24运输4.8吨，向销售点25运输6.72吨，向销售点27运输5.04吨，向销售点28运输6.23吨，向销售点29运输7.21吨.

④基地4：向销售点11运输3.35吨，向销售点12运输4.9吨，向销售点30运输9吨，向销售点31运输7.7吨，向销售点34运输5.56吨，向销售点35运输7.49吨.

⑤基地5：向销售点21运输3.95吨，向销售点22运输6.16吨，向销售点32运输8吨，向销售点33运输7.98吨，向销售点34运输2.91吨.

⑥基地6：向销售点8运输2.55吨，向销售点9运输7吨，向销售点10运输8.4吨，向销售点19运输5.11吨，向销售点20运输7吨，向销售点21运输4.94吨.

⑦基地7：向销售点1运输6.5吨，向销售点2运输4.6吨，向销售点7运输9.8吨，向销售点8运输4.1吨.

⑧基地8：向销售点2运输5.6吨，向销售点3运输8.4吨，向销售点6运输7.7吨，向销售点18运输6.3吨.

5 结论

根据前文计算出的结果进行计算，显然可以达到效率最大化的目的，因此本文的研究在实际生活中有一定的参考价值.同时，在考虑保证短缺量少于需求量的30%时，直接导致了政府补贴费用的飙升，增长了17.8%，而对于限定条件的考虑必定不多于实际情况下的限定条件，因此本文所做出的结果会相对偏小.