无限长直密绕通电螺线管磁场的一种简单计算方法

牛中明，于欣欣

（安徽大学 物理与材料科学学院，安徽 合肥 230601）

求解无限长直密绕通电螺线管的磁场分布是大学物理教材中经常使用的例子，但是，大部分教材都是直接假设螺线管内部为轴向的均匀磁场，而外部磁场为零，然后利用安培环路即可简单地得到内部磁场的大小[1].已有许多文献[2-6]针对该假设直接使用毕奥—萨伐尔定律或是使用对称性分析并结合安培环路定理进行了证明.但是，这些证明往往过于复杂，很难在实际的课堂中使用，因此很多教材由于篇幅的限制并未给出该假设的证明.为了培养学生认真严谨的学习态度，找出一种可以证明螺线管磁场分布假设的简单方法是必要的.本文将首先利用无限长密绕螺线管的对称性和毕奥—萨伐尔定律，对螺线管内外磁场的方向给出一种简单且严密地证明，然后再利用磁感应性的闭合性与安培环路定路，定量地求出无限长直密绕通电螺线管内外的磁感应强度.

1 无限长直密绕通电螺线管磁场的方向

由于螺线管无限长，因此由对称性可知，螺线管所有横截面对应点的磁感应强度相等.因此，只要确定了磁场在螺线管任一横截面上的分布，即掌握了整个螺线管的磁场分布.图1给出了无限长直密绕螺线管的横截面图，首先，在管内任取一点P，为了研究P点的磁场分布，图2给出了螺线管沿图1任一虚线的纵截面图.值得注意的是，图2上方导线截面的电流并不总是垂直于纸面向外，仅有当图2恰好是沿图1中虚线I的纵截面时，它才严格垂直于纸面向外，对于一般情况，如虚线II和III，其方向都是从纸面斜向外.

为了求出P点的磁感应强度，我们以P点对称地在A和B两处分别选择两个电流元，由于是纵截面，因此，A和B两处电流元的方向是一致的，在横截面中，其方向在图1中用箭头标出.因此，这两个电流元在P处产生的磁感应强度为

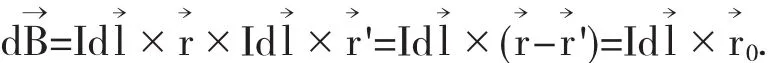
尽管dl→和r→0的方向并不总是垂直，但是由dl→和r→0共同确定的平面总是与图1的横截面平行，因此它们叉乘的方向必然沿着轴向，具体指向与电流

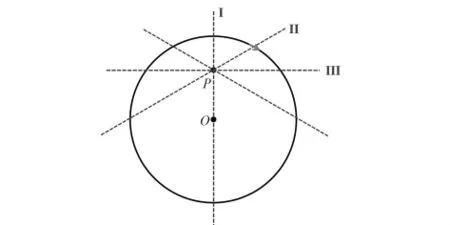
图1 无限长直密绕螺线管的横截面图

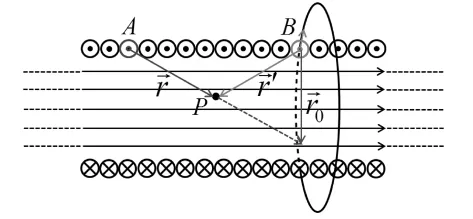
图2 螺线管沿图1任一虚线的纵截面图

方向满足右手螺旋关系.由于螺线管无限长，因此螺线管上任一点都存在与之对应的另一点，使其产生的总磁感应强度沿着轴向.综上可知，无限长直密绕通电螺线管中的磁感应强度必然沿着轴向，其具体指向与电流方向满足右手螺旋关系.同理可证，对于螺线管外部，其磁感应强度的方向也沿着轴向，但其具体指向与螺线管内恰好相反.

2 无限长直密绕通电螺线管磁场的定量计算

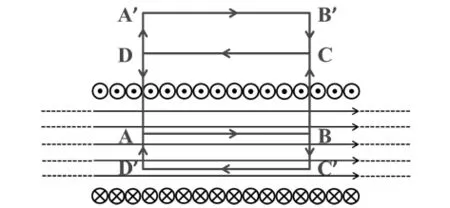
图3 通电螺线管安培环路的选择

知道了螺线管内外磁场的方向后，就可以进一步借助安培环路定理，定量地求出螺线管内外的磁感应强度.如图3所示，取回路ABC'D'A，然后由安培环路定理可知

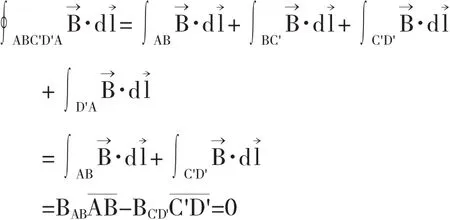
图4 与密绕螺线管轴线垂直的无限大平面S

如图4所示，作垂直于密绕螺线管轴线的无限大平面S，将管内部分的面积记为S内，管外部分的面积记为S外.那么，由于磁感应线是闭合的，因此

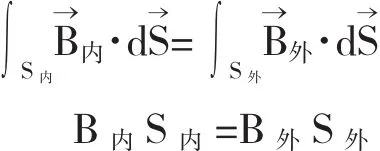
所以B外=B内S内/S外，由于B内和S内都是有限大小，而S外趋于无穷大，因此B外→0，即无限长密绕通电螺线管外部的磁感应强度与内部相比近似为零.

然后，再取图2中的ABCDA回路，并利用安培环路定理，有

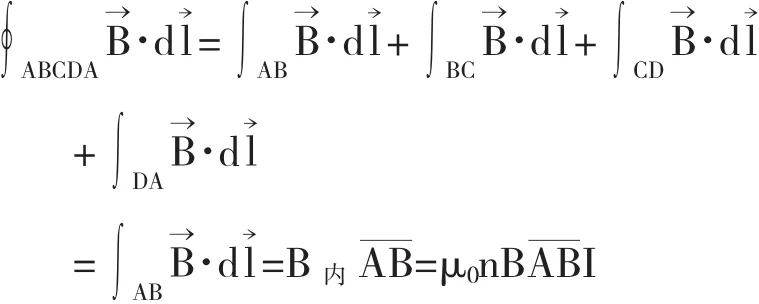
从而可得

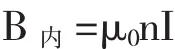
其中，μ0为真空磁导率，n为密绕通电螺线管单位长度线圈的匝数，I为密绕通电螺线管内的电流.

综上，无限长直密绕通电螺线管磁场外部磁场近似为零，内部磁场为匀强磁场，磁感应强度的大小为μ0nI，方向与电流方向满足右手螺旋关系.

3 结论

本文利用无限长密绕螺线管的对称性、磁感应线的闭合性以及安培环路定理，给出了一种简单且严谨地求解无限长密绕通电螺线管磁场分布的方法.根据笔者测试，发现使用该方法讲述该问题仅需10分钟左右.因此，在实际的课堂教学中，可以使用该方法讲解无限长密绕通电螺线管磁场分布的问题，这样能使学生在较短的时间内掌握该问题的严密求解过程，也有助于培养学生严谨求实的科学态度.