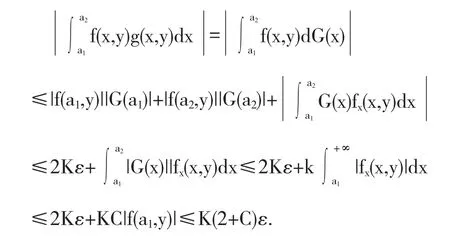两类狄利克雷判别法的推广

余 戡

（安庆师范大学 数学与计算科学学院，安徽 安庆 246133）

在高等数学[1]和数学分析[2]的教科书中，狄利克雷判别法是用来判别反常积分和级数收敛性的，因此占有相当重要的位置.众所周知，狄利克雷判别法中有单调递减趋于0的条件，文[3]中提出了弱于递减的RBV条件.

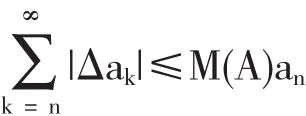
则称数列A为剩余有界变差数列，简记为A∈RBV（rest bounded variation sequences,RBVS）.

文[4]中，对常数项级数狄利克雷判别法条件进行的减弱，给出了狄利克雷判别法在RBV条件下的推广.

可以看出，定理2中也有单调递减趋于0的条件，根据文[4]的思想，我们将对反常积分的狄利克雷判别法进行推广，首先，类似于定义1，提出关于函数的RBV条件.

定义2 如果对于[a,+∞)上非负可微趋于0的局部绝对可积函数f(x)对任意b≥a，存在仅和函数f(x)有关的正常数C，满足

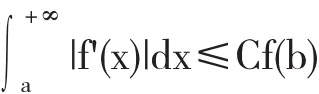
则称函数f(x)为剩余有界变差函数，简记为f(x)∈RBVF（rest bounded variation functions,RBVS）.

类似于定理1，建议如下定理.

证明 由已知可设存在M＞0，使得|G(y)|≤M，∀y∈[a,+∞]，并且∀ε＞0，存在 X，∀x＞X，均有 f(x)＜，由此结合分部积分法就有对任何a2＞a1＞X，有

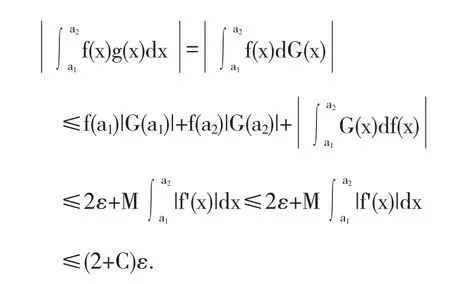
接下来讨论关于反常含参变量积分狄利克雷判别法[2]的推广，首先给出反常含参变量积分的狄利克雷判别法.

定理 4 设函数 f(x,y)，g(x,y)满足下列条件：（i）当A→+∞时，积分分关于 y∈[c,d]一致有界，即存在常数K，使得

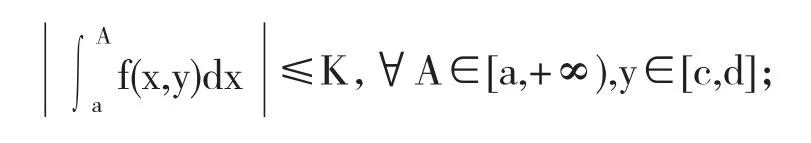
（ii）g(x,y)是 x的单调函数，且当 x→+∞ 时，g(x,y)关于 y∈[c,d]一致地趋于零，即任给 ε＞0，存在A0=A0(ε)，当 x≥A0时，|g(x,y)|＜ε,∀y∈[c,d]，则反常含参变量积分关于y∈[c,d]一致收敛.

接下来给出二元函数关于变量x的RBV条件.

定义3 如果对于[a,+∞)×[c,d]上非负对变量x可导且一致趋于0的关于变量x局部绝对可积函数f(x,y)对任意b≥a，存在仅和函数f(x,y)有关的正常数C，满足

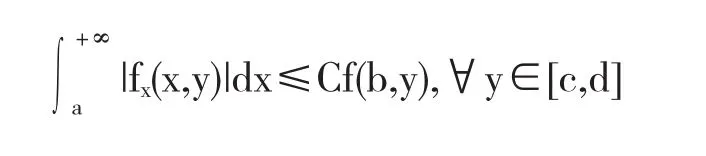
则称函数f(x,y)对x剩余有界变差，简记为f(x,y)∈xRBVF.

定理4可以推广为定理5.

定理5 设函数f(x,y),g(x,y)满足下列条件：

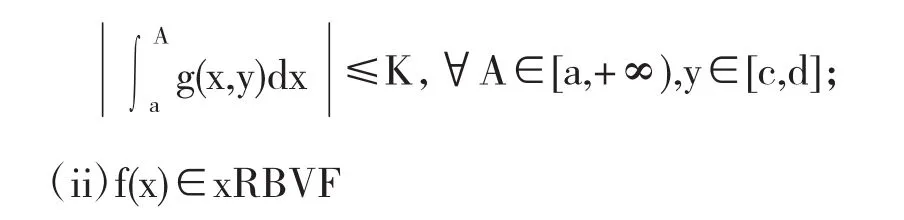
证明 由定义有任给 ε＞0，存在A0=A0(ε)，当x≥A0时，|f(x,y)|＜ε，∀y∈[c,d]，从而任给 a2＞a1＞A0