事件研究方法综述

2018-08-10黄晗，李明

统计与决策 2018年13期

黄晗，李明

（1.湖北商务服务发展研究中心；2.武汉工商学院，武汉 430065）

0 引言

事件研究法是基于有效市场假说（EMH）的理论框架，利用上市公司披露的信息，检验市场是否有效的一种重要实证方法。它广泛适用在商学领域，尤其是金融、财务方面的实证研究已有几十年的历史，至今在实证研究方法论上仍然扮演十分重要的角色。事件研究法最早可以追溯到Dolley（1933）的研究[1]，但是将事件研究法引入会计和金融领域的，分别是Ball（1968）[2]和Fama（1969）[3]的研究。主要目的是探讨当某些事件发生（或某些信息披露时），是否会引起股价的非正常变动，即是否会产生非正常收益率。利用事件研究法的文献，大致上可以分为4大类型[4]：①市场效率研究，这类研究主要评价股票市场是否快速、无偏地反映某些新信息；②信息内涵研究，即探讨信息的有效性，目的在于评价股票市场对某些信息的反应程度；③解释非正常收益率研究，目的在于进一步了解形成非正常收益的因素；④方法论研究，目的在于探讨事件研究法的改进，这类研究多以模拟的方式进行。本文将在回顾相关文献的基础上，对事件研究方法的研究设计和非正常收益率的估计及检验进行回顾，期望能够帮助使用事件研究方法的学者。

事件研究法一般包括以下6个步骤[1]：①识别感兴趣的事件；②定义事件窗口期；③选择哪些企业作为研究样本；④假设事件没有发生，预测事件窗口期中的“正常”收益率；⑤估计事件窗口期中的“非正常”收益率，此处的非正常收益率被定义为当事件没有发生的情况下，实际收益率与预测收益率之间的差异；⑥检验非正常收益率是否显著不为零。其中，前四步与研究者选定的问题和研究设计相关，因此，本文将以上6个步骤分为事件研究的设计、非正常收益率估计及统计检验、累计平均非正常收益率估计及检验3个部分进行介绍。

1 事件研究的研究设计

1.1 识别感兴趣的事件

事件研究法研究的事件可以分为两类：一种是同类事件的研究，例如研究会计盈余公告对股价的影响[2]，或者是研究雇佣CIO对股价的影响[5]，这样的研究事件类型相同，但是各个公司发布公告的日期可能不同；另一种是单一事件的研究，例如研究会计准则变更公布对股价的影响[6]，不但所有样本的事件类型是相同的，而且各个公司的事件日期也是完全相同的。如果披露的信息看上去有益于公司，则市场可能对其有正面的响应，反之，如果披露的信息看上去是不利于公司的，则市场可能对其有负面的响应。研究者为了尽可能精确地捕捉市场响应，一般希望获得较短的事件窗口期。因此，大多数事件研究使用日数据，但是也有一些研究使用其他频率的数据，例如一天之内的数据、周数据或者月数据。

1.2 定义事件窗口期

定义事件日是定义事件窗口期的前提，它是指市场“接收”到该事件相关信息的时点，而非该事件实际发生的时点。事件窗口期一般记为[-x,+y]，x是指事件日之前的天数，y是指事件日之后的天数，而事件日则被记为第0天。事件日能否准确的确认，将对事件研究的结果产生关键的影响。如果事件发生当天股票休市或停盘，则事件日可以重新定义为之后的第一个交易日。事件窗口期的长度并没有统一的标准，如果研究重点关注某一事件发生对股价是否有影响，通常将事件窗口期设定为事件日当天及前、后各1到5天。但是如果研究者有其他目的，例如想要知道事件公布之前，是否有信息泄漏则可以适当延长事件窗口期。也有些研究通过比较多个不同长度的事件窗口期[7]，对假设进行交叉验证。总之，事件窗口期应该覆盖事件造成影响的整个时期，同时又必须尽可能地小。

为了方便说明股票收益率的各种期望模型，将事件研究法中各种期间的时间定义如图1所示。事件发生或公布后股票收益率受到事件影响的期间为t3至t4，称为“事件窗口期”，共计W期（W=t4-t3+1）。

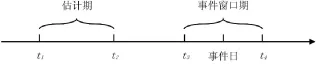
图1 事件研究法的时间线

1.3 研究样本的获得

样本公司的选择需要根据研究的事件而定。如果研究者希望研究中国上市公司的事件，信息来源主要来源是CSMAR经济金融数据库或者是Wind金融终端。如果这些数据库中没有感兴趣的事件，研究者也可以在巨潮资讯搜索上市公司的公告，统计事件日期。如果希望研究美国上市公司的事件，则可以访问沃顿研究数据中心（WRDS）获得事件信息，或者搜索LexisNexis数据库中上市公司的公告。关于事件信息的来源并不仅限于上述渠道，研究者也可以根据研究问题通过其他渠道获得，但是前提是需要准确的界定事件日。

1.4 估计期的选择

估计期是指事件尚未发生的那段时期。研究者可以利用这段时期，估计出在不发生该事件的情况下，事件窗口期内股票的期望收益率是多少。大多数研究将估计期选择在事件窗口期之前，但是不同的文献中对估计期的选择有三种方式：①估计期在事件窗口期之前；②估计期在事件窗口期之后[8,9]；③分别取事件窗口期之前和之后同时作为估计期[10,3]。根据Peterson[11]的建议，如果所要研究的事件不会造成预测模式结构上的改变，则估计期可以选在事件窗口期之前。如果所要研究的事件，改变了股票价格行为和市场行为之间的固有联系，而造成预测模式结构上的改变（例如事件本身造成公司资本结构改变），则估计期可以选在事件窗口期之后，或者同时选取事件窗口期前、后作为估计期。图1中t1至t2便是“估计期”，共计T期（T=t2-t1+1）。值得注意的是，事件窗口期与估计期不能重叠，只有这样，利用估计期对股票价格的估计才是无偏的。

关于估计期的长短，并没有客观和统一的说法[12]，一般由研究者自行确定。估计期太短可能会降低估计模型的预测能力，而估计期太长可能导致预测结构的变化[13]。不同的事件研究对于估计期的选择，从120个工作日[14]至255个工作日[15]不等。

1.5 估计正常（非事件）收益率模型的选择

假设某事件没有发生或者公布，样本股票的“期望”收益率为E(R̂iE)，这些收益率也可以被称为正常收益率。估计正常收益率种类繁多，常见的大致有三类方法：①平均调整收益率模型；②市场指数调整收益率模型；③风险调整收益率模型。为了方便说明，将各种符号定义如下：下标i代表样本股票；下标t代表时间；W代表事件窗口期的长度，即W=t4-t3+1；T代表估计期的长度，即T=t2-t1+1；下标E代表事件窗口期的某一期（一般为天）；N样本观测值的数量；Rit代表i样本股票在估计期第t期的实际收益率；Rmt代表第t期的市场收益率；ARit代表事件窗口期中第t期，i样本股票的非正常收益率；代表i样本股票在事件窗口期第E期的期望收益率。

1.5.1 平均调整收益率模型

该方法认为样本股票在没有事件影响时，事件窗口期中的期望收益率等于估计期中的平均收益率。即公式（1）所示。

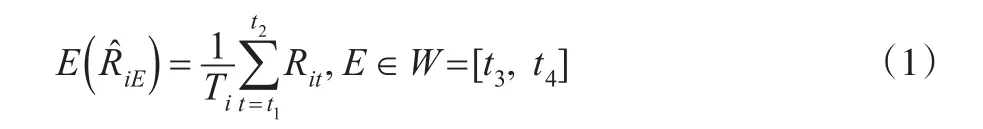
该模型在事件研究中被广泛使用，虽然与更高级的方法相比它不算很好，但也不是太差[16]。然而在有些情况使用该模型并不合适[17]。首先如果样本股票的事件日期离的非常近，出现“密集事件”时，发生第I类错误的概率将会增加，也就是实际上在事件窗口期并没有非正常收益率，但使用该模型估计非正常收益率时，却发现事件窗口期有非正常收益率。其次，如果事件日发生在牛市或者熊市，使用该模型得到的结果可能会偏高或偏低。发生上述问题的原因是因为平均调整收益率模型是取估计期的收益率平均值，如果估计期集中在牛市，则平均收益率将明显偏高，反之亦然。

1.5.2 市场指数调整收益率模型

该方法认为，在事件窗口期中，股票收益率的均值应该等于同一时期市场收益率的均值。即公式（2）所示，其中RmE为事件窗口期中的市场指数收益率。

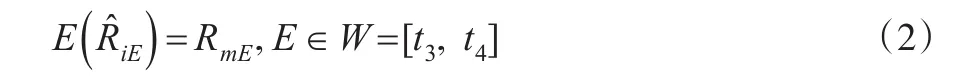
该方法不需要假设过去和将来存在某种联系，而其他利用过去的数据估计期望收益率的模型都暗含一个假设：以前存在的关系，以后也会存在。很显然，这是一个很强的假设，大多数情况可能并不适用。因此该方法对于那些在事件日之前没有（或不足）股票收益率信息的事件研究特别有用。例如对于股票刚刚上市的情况，其他模型无法使用，则可以使用该模型。如果研究美国的股票市场，则RmE一般使用标准普尔500指数的收益率；而研究中国的股票市场，则RmE可以被定义为沪深300指数。此外，根据Brown等[18]的模拟结果，使用等权重加权指数更有可能发现非正常收益率。

1.5.3 风险调整收益率模型

该方法是估计期望收益率最为常见的方法，它通过回归方法预测事件窗口期的期望收益率。具体而言就是将股票的系统风险，即β系数，作为股票收益率的预测因子。该模型有多种类型，例如市场模型、资本资产定价模型、Fama-French三因子模型、Carhart四因子模型、Fama-French五因子模型等。以上模型的复杂程度各有差异，其中以市场模型最为简单，但它的预测能力与其他复杂模型一样好[19]。

由于市场模型的应用最为广泛，此处仅以市场模型为例进行说明。首先通过最小二乘法（OLS）建立股票收益率的回归模型，如公式（3）所示。其中αi和βi为待估参数，εit为误差项。

接下来通过回归模型估计的参数计算股票在没有所要研究的事件影响时，事件窗口期的期望收益率，如公式（4）所示。其中和是根据估计期收益率计算得出，RmE是事件窗口期某一天的市场指数收益率。

2 非正常收益率估计及统计检验

2.1 非正常收益率的估计

不论是用上述哪一种方法估计事件窗口期中的正常收益率，估计非正常收益率AR的方法都是一样的，其计算如公式（5）所示。其中ARiE为i样本股票在事件窗口期第E期的非正常收益率，RiE为i样本股票在事件窗口期第E期的实际收益率，为i公司在事件窗口期第E期的期望收益率。

在计算每一个样本股票的ARiE之后，需要对所有样本股票的非正常收益率进行平均，称为平均非正常收益率（AARE），如公式（6）所示。其中AARE为在事件窗口期[t3,t4]中，某一期E，所有样本公司的非正常收益率求平均值后所得的平均非正常收益率；ARiE为第i家公司在事件窗口期[t3,t4]中，某一期E的非正常收益率，可由公式（5）得到。

在计算AARE之后需要对其进行统计检验，检验结果用来解释该事件是否对股价产生影响，这也是事件研究的重点。

2.2 非正常收益率的检验方法

平均非正常收益率检验的目的，主要是检验事件窗口期中每一期横截面平均非正常收益率及标准化非正常收益率是否显著地等于零。研究者将面临两个选择：①选择参数检验还是选择非参数检验的方式；②决定了参数检验或者非参数检验后，使用哪个统计量作为检验工具。目前大多数文献以参数检验为主，有些文献还辅以非参数检验。两种检验方式的区别在于参数检验假设非正常收益率符合正态分布，而非参数检验则无需对非正常收益率的分布作出任何假设[20]。因此通常的做法是为了增加结论的稳健性，同时采取两种方法进行检验。

常见的参数检验方式有t检验和z检验。不论是计算t值还是z值，分子都是AAR，分母都是AAR的标准差。而计算AAR的标准差时，其前提假设有很多差异，从而导致AAR的标准差也有多种计算方式，因此t值和z值的计算也有多种。

非参数检验统计量则有二项检验、符号检验、Wilcoxon符号序列检验、Kolmogorov-Smirnov单一样本检验及Mann-Whitney U检验。需要注意的是非参数检验并非可以无限制的应用，有些检验方法还是有前提假设的。例如Wilcoxon符号序列检验必须假设样本分布在平均值两侧是对称的；Mann-Whitney U检验假设两个样本必须是独立的等。

由于检验方法的复杂性，相互之间有很大的差异，所以此处仅介绍四种最为常见的检验统计量，其中前三种为参数检验，分别是：①传统方法；②标准化残差法；③普通横截面法；④非参数检验方法中的符号检验。

2.3 平均非正常收益率（AAR）的参数检验

参数检验的基础是假设股票的非正常收益率是服从独立的、一致的正态分布。而在实证过程中，单只股票的非正常收益率分布通常不是正态分布，尤其是股票日收益率的分布，往往是严重偏离正态分布的。但是根据中心极限定理，只要样本量足够大，横截面股票收益率的分布即可接近正态分布。针对AAR的参数检验，通常是计算t值或z值，计算公式如公式（7）所示，式中Var(AARE)为事件窗口期某一期E，横截面平均非正常收益率的方差，其平方根为平均非正常收益率的标准差；SAARE为事件窗口期某一期E，横截面标准化非正常收益率的平均值；Var(SAARE)为事件窗口期某一期E，横截面标准化平均非正常收益率的方差，其平方根为标准化平均非正常收益率的标准差。

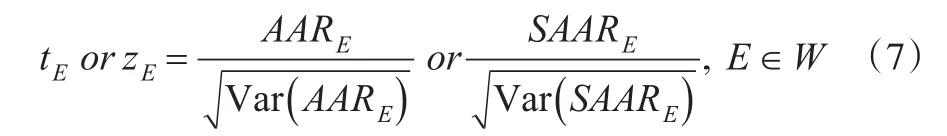
横截面单只股票非正常收益率为独立的、一致的正态分布假设是否成立，将直接影响Var(AARE)和Var(SAARE)的计算方式，因此产生了三种计算方法。

2.3.1 传统方法的t值计算

该方法检验事件窗口期某一期E的非正常收益率AR是否显著地不等于0的t值计算如公式（8）所示[18]。其中为估计期中，第i只股票在t期的残差项，即为第i只股票在估计期的期数，即为估计期中第i只股票残差项的方差，即为估计期的残差项的平均值，即，理论上应等于0或非常接近于0，根据估计非正常收益率的模型而定。

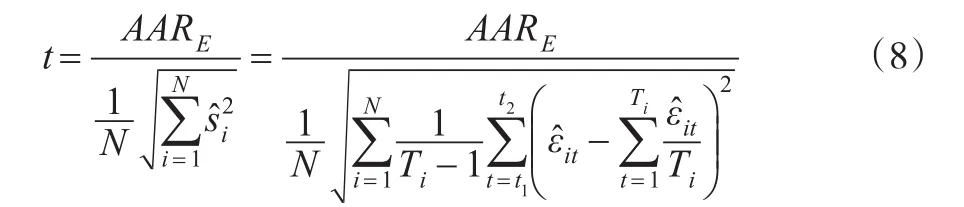
2.3.2 标准化残差方法的t值计算

该方法由Patell[21]首先提出，通过修正事件窗口期非正常收益率的方差，并在计算平均非正常收益率之前，将单只股票的非正常收益率进行标准化转换，使得单只股票的非正常收益率的分布服从单一的标准正态分布，如公式（9）所示。

2.3.3 普通横截面方法的t值计算

该方法的主要目的在于克服由于事件导致的变异问题。该方法在计算t值时，将完全忽视股票估计期残差的信息，而以事件窗口期股票收益率的横截面方差作为事件窗口期某一期E的平均非正常收益率方差。计算如公式（10）所示。

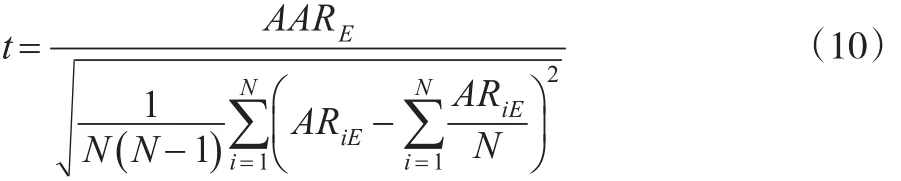
如果事件不会引起事件窗口期非正常收益率方差的增加，普通横截面方法的检验能力较弱[11]。

2.4 平均非正常收益率（AAR）的非参数检验

非参数检验的产生是由于参数检验假设股票收益率数据是正态分布，而实际中的数据很难达到正态分布的要求，从而导致不精确的推论[22]。常见的非参数检验包括秩检验[23]和符号检验[16]。本文仅介绍符号检验方法，该方法的特征只是关注事件窗口期的某一期中，横截面股票非正常收益率正、负比例是否显著的不等于50%。研究者根据所要研究事件的性质或研究目的，将样本进行适当的分类后，如果所要研究的事件对股票价格没有影响，那么横截面上股票非正常收益率为正、负的比例应当各占50%左右。符号检验的t统计量计算方式如公式（11）所示。

式中p为事件窗口期某一期E中，非正常收益率大于0的观测值占样本总数的百分比。

虽然有些研究[16]认为符号检验的检验效果不如t检验。不过并不妨碍研究者将其作为补充的统计量，以提高结论的稳健性。

3 累计平均非正常收益率估计及检验

当研究者无法确定事件日的准确日期时（或者其他因素），可能需要计算累计事件窗口期任意两期之间平均非正常收益率，来衡量该事件是否对收益率造成影响。常见累计任意两期之间平均非正常收益率的方式是计算“累计平均非正常收益率”，该方法由Fama提出并应用[3]。其计算方法如公式（12）所示，其中CAAR(τ1,τ2)为事件窗口期τ1到τ2的累计平均非正常收益率，即τ1到τ2的平均非正常收益率相加。

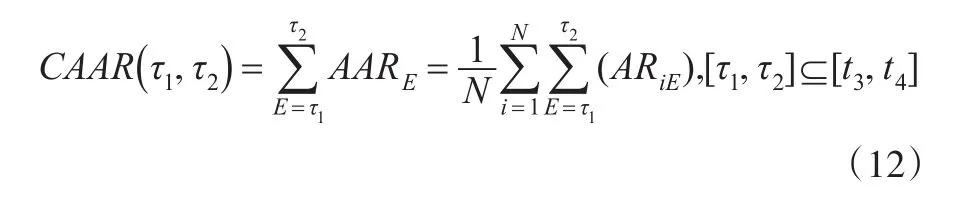
3.1 累计平均非正常收益率（CAAR）的参数检验

检验累计平均非正常收益率（CAAR）或者标准化累计平均非正常收益率（SCAAR）与检验AAR及SAAR的方式与逻辑是一样的。本文仍然介绍三种参数检验和一种非参数检验方法。

假设在检验事件窗口期中，τ1期至τ2期共计m期（m=τ2-τ1+1），且τ1,τ2∈W=[ ]t3,t4，则累计平均非正常收益率（CAAR）或者标准化累计平均非正常收益率（SCAAR）的统计检验如下。

3.1.1 传统方法的t值计算

该方法在文献中应用最为广泛，其t值计算如公式（13）所示。

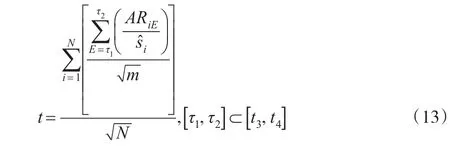
有些文献以事件窗口期某一期E的非正常收益率的方差，即以代替固定的。有些研究[24]认为在假定股票非正常收益率的横截面独立，且该事件不会引起事件窗口期股票收益率变异增加的情况下，其检验能力较好。但是也有学者[25,26]认为该统计量有过度拒绝原假设的误差（犯第I类错误的可能性增加）。

3.1.2 标准化残差方法的t值计算

该方法主要由Patell（1976）[21]提出，其计算如公式（14）所示。个别研究[26]表明，该方法比传统方法表现更好。

3.1.3 普通横截面方法的t值计算

该方法未见文献上的探讨，但是根据检验AAR的方式，检验CAAR的t值公式如（15）所示[4]。其中CARi(τ1,τ2)该方法的优缺点与其检验AAR的统计量类似，不再赘述。

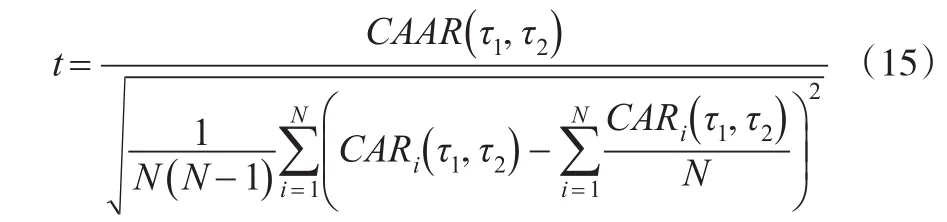
3.2 累计平均非正常收益率（CAAR）的非参数检验

此处仍然只介绍符号检验法。由于符号检验法只关注CAR及SCAR为正的比例是否显著不为50%，因此其检验公式与检验AR及SAR的公式（11）一样，只是p定义为CARi(τ1,τ2)或SCARi(τ1,τ2)大于0的观测值。

4 事件研究方法的发展

事件研究方法经过五十多年的发展，已经为资本市场方面的研究作出了巨大贡献。而且其应用范围也在不断扩展，除了会计和金融学科，其他很多学科也使用该方法进行研究。事件研究的基本结构——即通过对市场模型预测的偏离程度来反应异常收益率，与Fama等（1969）[3]引入该方法时的基本结构相同。但是对异常收益率的统计检验却一直在不断发展，并成为该方法的研究热点[22]。关于AR、CAR的检验只能回答所要研究的事件对股价是否有显著影响，如果需要进一步了解影响事件窗口期非正常收益率的影响因素，研究者可能需要进一步探讨。这类研究在计算样本的AR或CAR之后，将AR或CAR为被解释变量，通过回归模型进行下列关系的横截面分析：

例如研究企业发布会计盈余的公告对股价的影响，那么AR、CAR可能受到未预期盈余大小、暂时性盈余及市场要求的收益率等因素的影响[27]。这类研究问题可以通过下列类似的回归方程进行分析：

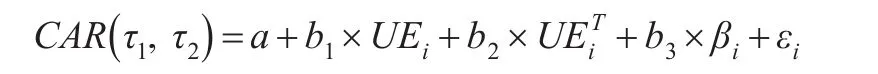
式中UEi为i公司未预期盈余，即i公司公告的盈余与市场预期之差；为i公司未预期盈余UEi中包含的暂时性盈余，例如非营业收入及支出等；βi代表i公司的系统风险，风险越高，市场要求的收益率越高；εi为i公司的残差项。如果市场真的利用公司公告的会计盈余，预测公司未来现金流量的变动。那么b1应该显著大于0，即未预期盈余越大，市场对公司未来现金流量变动的预期就越大，股价的反应（即非正常收益）就越大；b2应该显著小于0，因为暂时性未预期盈余，影响市场对公司未来现金流量变动的预期较小；而b3则应该显著小于0，因为公司的风险越大，市场要求的收益率就越高，对未来现金流量变动的折现值就越小关。该方法在其他领域也使用的非常普遍，例如探讨产品召回事件对股价的影响以及哪些因素影响了AR[28]。