非平行板电容器测量杨氏模量的改进

唐子彦，冷文秀

(中国石油大学(北京) a.地球物理与信息工程学院；b.理学院，北京 102249)

杨氏模量是描述固体材料抵抗形变能力的物理量，有着重要的意义. 在大学物理实验课中有静力拉伸法测量杨氏模量的实验. 使用非平行板电容器测量杨氏模量的方法大致分为2种：传统式结构[1]和差动式结构[2]. 但这2种方法因装置结构的限制，在可操作性、系统误差、灵敏度上都有改进的空间. 本文提出的中心轴差动式结构,对上述问题进行改进.

1 基本原理

1.1 理论计算

C2=C2′,

(1)

图1 非平行板电容器

所以偏转前的电容器的总电容为

C总′=C1′+C2′,

(2)

偏转后的电容器的总电容为

C总=C1+C2.

(3)

由文献[6]知,在忽略边缘效应的情况下电容器的电容为

(4)

将(4)式作泰勒展开得：

(5)

当θ足够小时，sinθ≈θ，故(5)可近似变为

(6)

令

则

C1=α0+α1θ+α2θ2+α3θ3+α4θ4+…

(7)

由(3)式可知偏转后的电容器总电容为

C总=C2+α0+α1θ+α2θ2+α3θ3+α4θ4+…

(8)

由(2)式可知偏转前(θ=0)的电容器的值为

C总′=C2′+α0,

(9)

式(8)与式(9)做差，由(1)式得

|ΔC|=|C总-C总′|=α1θ+α2θ2+α3θ3+α4θ4+…

(10)

若略去θ的二次项及以上的高次小项，得

|ΔC|=|α1θ|,

(11)

将α1代入式(11)，得

(12)

结果与文献[1-2]中电容改变量完全一致.

最后利用电桥法测出偏转前后电容器的改变量|ΔC|，由(12)式求出θ，通过测量钢丝的直径，计算出横截面积S，钢丝原长L，电容器转动轴到钢丝的距离D,再由杨氏模量的定义式及文献[1]可以求出杨氏模量为

(13)

1.2 中心轴差动式结构电容的分析

如图2所示，该结构的电容器由3部分组成. 图2中上、中、下的白色部分为长宽为a的矩形金属板，而图中的阴影部分为刚性强度较大的绝缘材料，其长度相对于a可忽略不计，即远小于a. 将上中下3个极板间的电容分别视作C11，C12，C21，C22，若只考虑常数项和一次项，由(7)式得：

图2 中心轴差动式结构电容器

C11=C22=α0+α1θ,

(14)

C12=C21=α0-α1θ.

(15)

令ΔCⅠ=ΔC11+ΔC22，ΔCⅡ=ΔC12+ΔC21，则由式(11)得：

ΔCⅠ=2|α1||θ|,

(16)

ΔCⅡ=-2|α1||θ|.

(17)

式(16)与式(17)相减得：

|ΔCⅠ-ΔCⅡ|=4|α1|θ.

(18)

使用电桥法测量出式|ΔCⅠ-ΔCⅡ|，即可计算出θ，再将θ代入式(13)可算出杨氏弹性模量E.

2 改进后的实验装置及其可操作性

2.1 实验装置简介

如图3所示，改进的主要方案是将文献[2]装置位于中间极板边缘的转动轴移至中心轴处，以组成中心轴差动式结构.

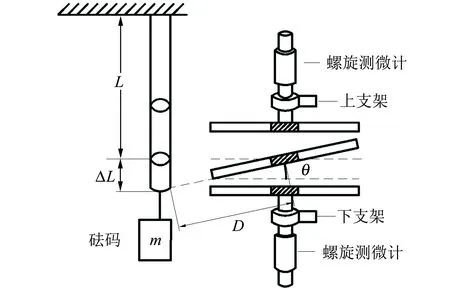
图3 实验装置图

本文所提出的的测量方案与文献[2]类似：先使用长宽均为2a的矩形金属板作为该电容器的上、中、下极板，并将螺旋测微计的测微螺杆的端面与电容器上下极板连接，然后将上下极板固定在绝缘支架上；中间极板的阴影部分与同为刚性强度较大的绝缘材料制成的转动轴相连，并使转动轴的位置固定.

实验时，为使钢丝保持拉直，首先在钢丝下的砝码盘上放上砝码，然后把钢丝与中极板靠近钢丝的一端用绝缘刚性材料连接，松开固定上、下两极板的固定旋钮，使该电容器的3个极板完全重合后再通过调节螺旋测微计使极板间距变为d且保持中间极板平行，通过电桥测出电容，从而得出电容的改变量.

2.2 可操作性

2.2.1 可操作性及系统误差

原有的2个实验装置在理论上都提出了测量杨氏模量的装置，但是由于装置结构的限制在可操作性上都存在问题，如在将钢丝与转动极板相连前，由于极板的转轴位于其末端，极板会因为自身重量和转轴摩擦不能平衡而发生一定程度的偏转，会影响钢丝发生形变时的伸长长度，或者理解为极板发生转动的角并不完全因为钢丝形变而产生，一部分转动是由于极板自身重量而产生. 针对上述2种装置可操作性存在的问题，本文提出的装置结构将转轴的位置放置于极板中间使得极板可通过自身重量保持平衡在实验开始前并不发生转动，让角的改变尽可能通过钢丝形变产生，使实验的可操作性提高的同时大大降低系统误差.

2.2.2 另一种实验方式

当被测物体为柱状时可以使用图4所示的实验装置进行测量，电容器部分的结构与图3一致，因被测物为柱状物体，所以可以用已知质量的重物或者已知大小的压力作用在物体的顶端，即可更准确、误差更小地测量出杨氏弹性模量.

图4 实验装置图

3 灵敏度、误差分析及测试结果

3.1 电容器的灵敏度

用电容的响应量(即电容的改变量)ΔC和初始时的电容C0之比来表示灵敏度[7]，记作s，不考虑边缘效应和分布电容的影响，可得

(19)

如图1所示，文献[1]中电容器的改变量ΔC1为

ΔC1=α1θ,

(20)

由式(19)及式(20)得文献[1]中装置灵敏度s1为

(21)

由文献[2]知：

ΔC2=2α1θ,

(22)

所以文献[2]中实验装置的灵敏度s2为

(23)

中心轴差动式结构的灵敏度记作s3，由式(18)知：

ΔC3=|ΔC1-ΔCΠ|=4|α1|θ,

(24)

由此得

(25)

通过对比式(23)及式(25)可得

s3=2s2=4s1.

(26)

可以得出结论：在电容器的灵敏度方面，本文中的中心轴差动式结构有了很大的提高，分别是文献[1]和文献[2]装置灵敏度的2倍和4倍.

3.2 相对非线性误差

文献[2]中已详细给出相对非线性误差的计算过程，中心轴差动式结构在相对非线性误差上与文献[2]相同，也就证明了相对非线性误差远小于文献[1]，使相对非线性误差大大降低.

3.3 测试结果

利用本装置测得的钢丝的杨氏弹性模量E=(1.98±0.43)×1011N/m2. 由实验结果可以得出：在理论和实践中，使用本装置进行杨氏弹性模量的测定都符合实际要求.

4 结束语

基于非平行板电容器的杨氏模量测量装置，采用中心轴差动式结构. 转轴设置于中极板的中心处，边缘效应和测量系统的分布电容对实验的影响被基本消除，在中极板与钢丝连接之前，中极板可通过自身重力保持平衡，以免在实验开始之前中极板发生偏转，使实验过程中得到的中极板的转动角度更加精确. 测试结果表明本装置能有效地提高电容器测法测量杨氏弹性模量的精确度和灵敏度，降低系统误差.