基于SNOP的柔性配电网中分布式电源最大准入容量计算
2018-08-08梁海深李盛伟白临泉刘聪李维徐健王庆彪
梁海深,李盛伟,白临泉,刘聪,李维,徐健,王庆彪
(1.国网天津市电力公司宝坻供电分公司,天津市 301800;2.国网天津市电力公司经济技术研究院,天津市 300010;3.ABB,美国北卡罗来纳州罗利市 27606; 4.国网天津市电力公司检修公司,天津市 300010)
0 引 言
近年来,分布式发电技术获得了越来越广泛的应用,各种分布式电源(distributed generation,DG)的并网发电对电力系统的安全稳定运行提出了新的挑战。当传统中、低压配电网中的分布式电源容量达到较高的比例(即高渗透率)时,要实现配电网的功率平衡与安全运行,并保证用户的供电可靠性和电能质量,存在一定的困难[1],因此,配电网如何消纳DG成为了热点研究课题。
以往对配电网消纳DG能力的研究,主要是根据配电网潮流、拓扑结构等限制条件,得出允许接入配电网的DG容量之和[2],并且主要针对传统配电网进行研究。如文献[3]考虑DG接入位置、出力大小以及渗透率等因素对配电网的影响,提出了配电网中分布式电源运行域的概念,可得到给定节点DG准入容量范围。文献[4]提出了一种柔性配电网(flexible distribution network, FDN)概念,它以一种新型电力电子设备,即智能软开关(soft normally open point, SNOP)的应用为基础,为提高配电网对DG的消纳能力提供了新的可能[5-6]。SNOP技术旨在以可控电力电子变换器代替传统基于断路器的馈线联络开关,从而实现馈线间常态化柔性“软连接”,能够提供灵活、快速、精确的功率交换控制与潮流优化能力。
目前对SNOP的研究主要集中在配电网运行优化方面[7-10],SNOP通过准确控制两侧有功功率交换,并根据需要向两侧分别提供无功补偿来优化全网潮流分布,提供了现有配电自动化体系所不具备的实时、精细的潮流调节优化能力,能够快速跟踪分布式能源和负荷的动态变化,降低网络损耗,确保配电网实时处在最优的运行状态。文献[11]采用一种基于模拟退火和锥优化的混合算法来提高含SNOP配电系统经济性,其核心目标仍为降低网损。
事实上,除了配电网运行优化方面的应用,SNOP也可用于提升DG消纳能力。在FDN中,依靠SNOP的双向功率调节能力,可改善配电网中电压瓶颈节点和传输容量瓶颈支路的运行状态,从而突破文献[3]中的运行域,实现DG高比例接入。在依靠SNOP提高DG消纳能力方面已形成一些研究成果。文献[12]探讨了SNOP对配电网中光伏准入容量的提升作用。文献[13]分别针对英国城网和农网进行研究,指出SNOP的无功功率支撑能力是提升DG消纳率的关键。文献[14]主要从平抑光伏出力波动角度研究了储能和SNOP配合对DG消纳能力的提升。但上述研究均未从规划角度得出FDN中DG准入容量最大时,DG和SNOP的最优位置、容量组合。
本文将建立FDN中DG最大准入容量模型。由于该问题为高维非线性优化问题,采用一种多种群遗传算法来求解,可避免陷入早熟收敛,得到全局真实最优解,并使用IEEE 33节点配电系统进行算例分析。在计算SNOP对既定节点位置的DG接入能力提升作用的基础上,进一步探讨FDN中全网DG自由接入的最优节点位置和容量组合,从而得到FDN中的DG最大准入容量。
1 FDN中DG最大准入容量模型
1.1 SNOP应用概述
最主流的SNOP装置是背靠背电压源型变流器(back-to-back voltage source converter,B2B VSC)。SNOP通常接入于传统的联络开关位置,如图1所示。不同于传统的联络开关只能处于0、1这2种状态,SNOP具有灵活的四象限功率控制能力,能够在2条馈线间进行主动潮流控制,该特性不论对于降低配电网网络损耗或是改善节点电压水平、支路电流均有重要意义。
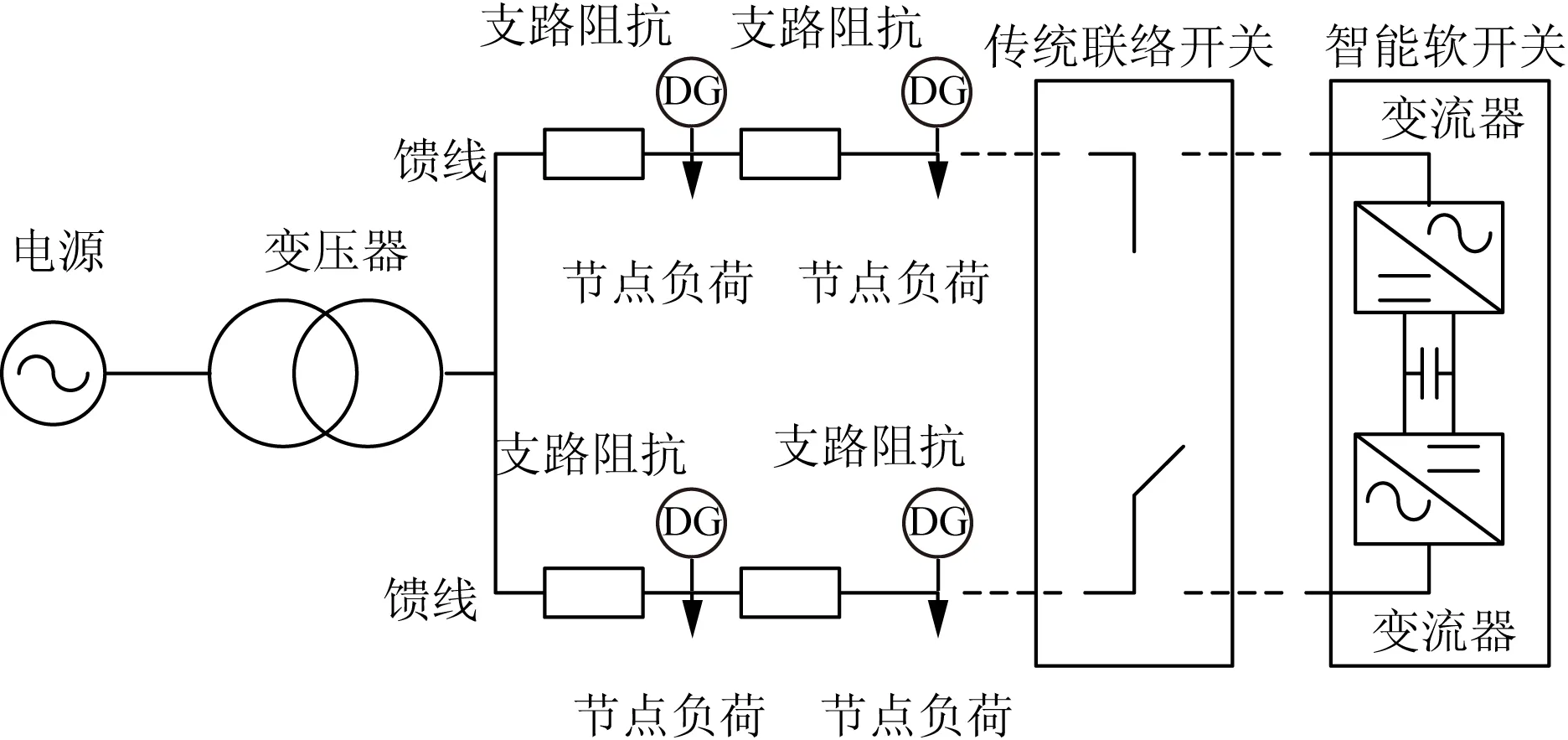
图1 SNOP接入位置Fig.1 Position of SNOP installation
1.2 DG接入FDN极限容量计算模型
DG的接入将改变传统配电网的潮流分布特性,对配电网稳态运行造成冲击。一方面,DG高比例接入,将引起接入节点的电压大幅提升,另一方面,DG接入比例过高可能突破馈线容量限制。而FDN依靠SNOP的潮流控制能力,能够优化潮流分布,防止稳态指标越限,从而提高DG的准入容量。
由于DG与负荷对网络电压的影响相反,DG接入最严苛的场景为负荷最小,同时DG处于峰值出力的场景,此时DG输出功率等于装机容量。本文探讨的DG准入容量即基于该场景,所得准入容量为“安全容量”。考虑到DG出力的随机性,当DG以该容量接入时,不论出力如何变化,均不会导致因DG接入量过大造成潮流越限。
建立DG准入容量模型,选择最大化FDN中DG接入容量作为优化目标:
(1)
式中:EDG,i为网络中各个节点的DG接入容量;N为网络中节点数目。
模型主要约束如下:
(1)网络潮流约束:
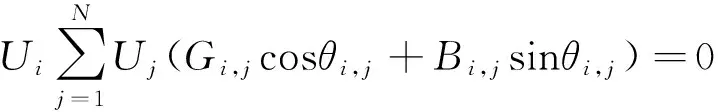
(2)
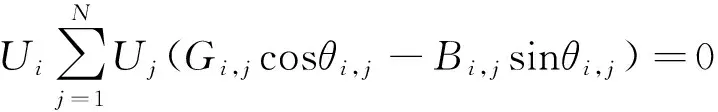
(3)
式中:PDG,i、PSNOP,i和PL,i分别为节点i上DG,SNOP和负荷注入的有功功率;QDG,i、QSNOP,i和QL,i分别为节点i上DG,SNOP和负荷注入的无功功率;Ui、Uj、θi,j分别为相连节点i、j的电压幅值和相角差;Gi,j、Bi,j为互电导和互电纳。
本文讨论场景下,DG以峰值出力,输出功率等于装机容量,所以式(2)中的PDG,i即为式(1)中的EDG,i。
(2)馈线容量和节点电压约束:
Ci≤Cmax
(4)
Umin≤Ui≤Umax
(5)
式中:Cmax为馈线最大容量;Umin和Umax分别为节点电压上限和下限。
(3)分布式电源单点最大准入容量约束。按照配电网规划设计原则,分布式电源在特定的电压等级下有其极限接入容量,超过时应接入更高电压等级的配电网。
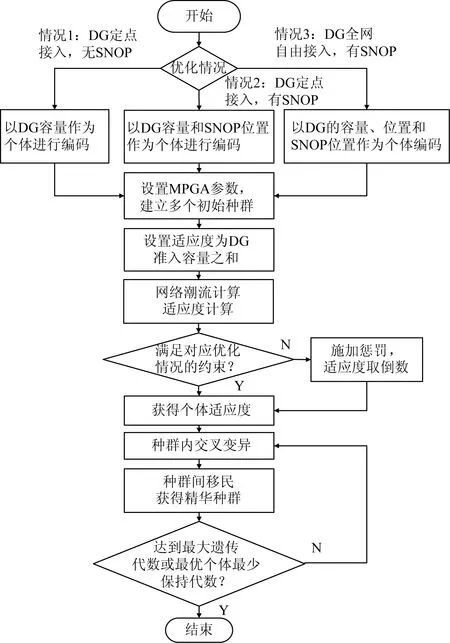
EDG,i (6) 式中EDG,max为特定电压等级下的单点DG极限接入容量。 (4)SNOP功率约束[11]: PSNOP,i+PSNOP,j=0 (7) (8) (9) 式中SSNCP,i和SSNOP,j分别为节点i、j上变流器的容量。 需要指出,上述模型通过提前设定好部分参数值,可以实现特定的优化和分析功能,具体可分为3种情况: 情况1:DG定点接入,无SNOP。DG接入的节点位置由人为设置,容量作为变量;SNOP相关位置、容量参数置0。该情况可考察网络不同节点对DG的接纳能力。 情况2:DG定点接入,有SNOP。DG的节点位置由人为设置,容量作为变量;SNOP的容量固定,接入位置作为变量。该情况可考察SNOP对DG准入容量的提升作用,以及SNOP在网络中的最优接入位置和运行状态。 情况3:DG全网自由接入,有SNOP。DG接入节点位置,容量均为变量;SNOP的容量固定,接入位置为变量。可考察SNOP以及DG的最优选址、定容组合方式。 该模型的优化变量为各个节点的分布式电源出力以及SNOP流过的有功功率和双侧无功功率。由于配电网规模可能达到数百节点,该模型属于高维非线性优化问题。这种问题的求解关键在于获得全局最优解。同时从规划角度,对于算法的全局收敛能力要求高于收敛速度。遗传算法(genetic algorithm,GA)是一种广泛使用的基于进化机制的高度并行、随机、自适应的全局优化概率搜索算法,由于优化时不依赖梯度,具有较强的鲁棒性和全局搜索能力,但是容易陷入早熟收敛问题,其计算结果受控制参数影响较大。为克服未成熟收敛,需要根据实际问题,进行复杂的控制参数和遗传算子设计研究。 本文采用一种多种群遗传算法(multiple population genetic algorithm,MPGA)来求解模型。MPGA的优势在于突破传统遗传算法仅靠单个种群进行遗传进化的框架,引入多个种群同时进行优化搜索;多个种群之间通过遗传算子进行联系,实现多种群的协同进化,最优解的获取是多个种群协同进化的综合结果。 相对于标准GA,MPGA采用了多个种群同时对解空间进行协同搜索,兼顾了算法的全局搜索能力和局部搜索能力,计算结果对遗传控制参数的敏感性大大降低,对克服未成熟收敛有明显效果,适用于所需求解的高维非线性优化问题。 采用MPGA求解模型时,适应度即为式(1)中的全网各节点DG准入容量之和。针对1.2节所述3种情况的优化问题,可通过不同的变量参数设置进行求解,计算方法如图2所示。 本文以IEEE 33节点配电系统为例进行分析,如图3所示。 图2 MPGA算法流程图Fig.2 Flow chart of MPGA 图3 IEEE 33节点配电系统Fig.3 IEEE 33-bus distribution system 图中TS1—TS5为5个联络开关,全部断开。该网络首端基准电压为12.66 kV,馈线额定容量为5.28 MW。网络基础负荷为3 715+j2 290 kV·A,是该网络必须满足的最小负荷。参考《电能质量供电电压允许偏差》(GB12325-2008),设定电压允许偏差值为-7%~7%,即网络安全电压标幺值为0.93~1.07 pu。根据《国家电网公司配电网规划设计技术导则》,式(6)中的分布式电源接入10 kV电压等级不应超过7~8 MW,本算例取7 MW。 经潮流计算,该配电系统传输容量最大的支路为0-1支路,容量4 645 kV·A。各节点电压如图4所示。 图4 配电系统节点电压Fig.4 Node voltage in distribution system 由于感性负荷将拉低电压,该配电系统电压呈现自平衡节点0至馈线末端逐渐降低的特点。其中节点8—17,28—32低于0.93 pu的安全电压下限,需接入分布式电源提升节点电压。 本文分布式电源设为PQ型,功率因数为0.95。优化过程中,MPGA算法基于MATLAB程序实现,并调用GADST遗传算法工具箱。算例中,MPGA种群大小设为500,最大迭代次数设为200,种群精英数设为10,交叉后代比例取0.75,最优个体最少保持代数设为20。计算过程中,设定50代内适应度函数值的加权平均变化值小于1×10-6,则算法停止。 为考察不同节点接入DG的能力,按图2流程中优化情况1方法,计算各节点DG准入容量,结果如表1所示。 由此可将不同节点的DG准入容量分为4类: (1)DG接入节点1,18—21。该类节点接入DG后无法提升节点8—17,28—32电压至安全范围内,故接入无效。 (2)接入节点7—17,27—32。该类节点位于馈线末端,DG准入容量较小。 (3)接入节点6,22,23,25,26。该类节点位于各馈线分支的前端,DG准入容量较大。 (4)接入节点2—5。该类节点位于整个33节点配电系统的网络前端,DG准入容量最大。 在上述4类节点中,分别选择节点18,30,22,5这4个节点以最大准入容量接入DG(节点18以7 000 kW接入),对应网络电压如图5所示。 依据表1和图5可得出如下结论: (1)接入DG将改变配电系统网络电压分布,造成接入点及周边节点的电压升高,这种影响随与接入节点的距离加大而逐渐减小。 表1网络不同节点的DG准入容量 (2)接入点越趋近于长馈线末端,则DG准入容量越小。这是由于相比其他节点,长馈线末端节点电压对DG接入更敏感,DG无功主要作用于接入节点,使其更容易达至安全电压上限。 (3)随着接入位置向馈线首端迁移,DG准入容量增大。这是由于DG的无功影响得以全网扩散,导致接入点电压敏感性降低。馈线容量限制逐渐成为瓶颈因素。 (4)当接入位置达至网络首端各节点,准入容量进一步提高,限制DG准入容量进一步提升的因素变为该电压等级DG单点准入容量。 图5 引入DG后配电系统节点电压Fig.5 Node voltage in distribution system with DG (5)原33节点配电系统2条馈线存在电压越安全下限的情况。在这2条以及相邻的2—24馈线接入DG有助于提升其电压至安全范围。但馈线18—21为这2条馈线的非相邻馈线,电气联系较弱,接入DG无效。 在上述4类节点中,前2类仍有较大的DG准入容量提升空间。引入SNOP形成FDN,SNOP1—SNOP5分别代表图3中TS1—TS5位置的SNOP。考察DG在单点(18/30)、多点单馈线(14、17)、多点多馈线(17、32)3种接入方式,SNOP不同接入位置对准入容量的提升作用。SNOP容量设定为双侧1 MV·A。采用图2中优化情况2的方法进行计算,结果见表2—4。表中P1代表SNOP小号节点侧的有功功率,Q1代表SNOP小号节点侧的无功功率,Q2代表SNOP大号节点侧的无功功率。SNOP有功功率以向小号节点发出功率,从大号节点吸收功率为正;无功功率以从节点吸收功率为正。 表2SNOP对DG单点接入时准入容量提升作用 表3 SNOP对DG多点单馈线接入时准入容量提升作用Table 3 Promotion of SNOP to the allowable DG penetration capacity in multi-bus/single-freeder scenario 表4 SNOP对DG多点多馈线接入时准入容量提升作用Table 4 Promotion of SNOP to the allowable DG penetration capacity in multi-bus/multi-branch scenario 由优化结果可见,SNOP的潮流控制能力能够提升DG准入容量。不同的DG和SNOP接入方式,体现出如下不同特点: (1)节点30单点接入DG时,对节点30准入容量提升最大的SNOP1和SNOP5均为与30节点所在支路直接相连的软开关,并且均处于双侧吸收无功功率,从30节点所在支路吸收有功功率的运行方式。 (2)节点18单点接入DG时,由于无法抬升全网电压至安全范围,接入无效。而通过在节点18所在馈线接入SNOP3/SNOP4,与其他馈线在末端产生了潮流联系,DG得以高比例接入配电网。 (3)选择DG多点(14、17)单馈线接入配电网时,优化结果为位置靠前的14节点以极限容量接入,而17节点不接入。引入SNOP后,DG准入容量得到了一定提升。一方面,SNOP1/SNOP3/SNOP4均从14、17节点所在馈线吸收有功功率,将其转移到其他馈线,起到降低DG接入馈线电压的作用(SNOP2两端均位于该馈线,有功传输功率为0;SNOP5与该馈线无直接联系)。另一方面,SNOP在双侧吸收无功功率,进一步拉低网络电压,为DG接入提供了更大空间。SNOP以其有功、无功功率同时双向控制能力,相比传统的无功补偿装置SVG等,在消纳DG方面能够取得更好的效果。 (4)选择DG多点(17,32)多馈线接入配电网时,SNOP1分别在两侧联系2条馈线,双端均以满容量吸收无功,可取得最优准入容量提升效果。 综上,SNOP能够对DG准入容量起到提升作用。提升幅度最大的SNOP须至少一端与DG所在馈线直接连接,处于双端吸收无功功率运行方式,并且无功功率在SNOP容量中占主导。 设DG接入节点17和32,考察不同容量SNOP对DG准入容量的提升作用。SNOP设定位于图3中TS1位置。做SNOP容量对DG准入容量影响的灵敏度分析,从网络电压、DG准入容量、瓶颈支路容量3方面考察接入不同容量SNOP的效果,结果如图6、7所示。 电压方面,不同SNOP容量下,电压曲线基本保持一致,节点17和32的电压均为瓶颈因素。 支路容量方面,支路4—5位于5—17,5—32这2条馈线的潮流交汇处,为传输容量瓶颈支路。随着SNOP容量的提升,支路4—5的传输容量呈先抑后扬的特点。这是由于当SNOP以小容量接入时,双端吸收无功功率,抵消了一部分DG的无功输出,导致4—5支路容量下降。随着SNOP容量的提升,DG准入容量也相应提升,支路4—5容量不断增大。当SNOP容量达到2 000 kV·A时,4—5支路容量达到5 280 kV·A的瓶颈,与电压一同成为限制DG准入容量进一步提升的因素,此时DG准入容量增速开始放缓。在该DG和SNOP接入位置下,2 000 kV·A是SNOP的经济容量。 图6 不同SNOP容量下网络节点电压Fig.6 Node voltage in distribution system with different SNOP capacities 图7 不同SNOP容量下DG准入容量和瓶颈支路容量Fig.7 Allowable DG penetration capacity and bottleneck branch capacity with different SNOP capacities 需要指出,不同的DG、SNOP接入点,灵敏度分析和经济容量结果将不尽相同。 上述分析主要针对既定DG接入位置下,FDN中DG最大准入容量。从规划角度,为了实现全网DG最大容量接入的目标,如何确定当DG在网络各节点自由接入时,DG的最优位置/容量组合及与其相配合的SNOP接入方式,是需要关心的问题。 采用图2中优化情况3的计算方法进行优化。考虑到SNOP的经济性,仅使用1台SNOP,容量设为双侧1 MV·A。经过多次优化计算,可得到多种DG集中和分散接入的方案,其全网DG准入容量相近。仅挑选4种集中接入的方案列于表5中。 表5DG自由接入优化方案 如表5所示,仅配置单台双侧1 MV·A的SNOP,可接入DG容量达到了9 400 kW以上,能量渗透率250%以上。以上方案可作为DG和SNOP规划时的推荐方案。应用本文方法,也可得到其他SNOP容量或多组SNOP共同接入时的最优方案。 (1)配电网的长馈线末端电压对DG接入敏感,容易造成电压越限,不利于DG接入。 (2)FDN中的SNOP通过主动控制潮流分布,改善网络电压状况,相比传统配电网能够提高DG准入容量。对于既定DG接入位置的FDN,SNOP应至少有一端布置在DG所接入的馈线上,以双端吸收无功功率方式运行,从而取得最大的容量提升效果。 (3)对于DG自由接入的FDN,存在多种集中或分散接入的方案,可获得接近的DG准入容量。 需要指出,受限于当前电力电子技术和设备的发展水平,SNOP的工程应用尚未成熟,成本偏高。但其占DG整体投资比例不大,而在提升DG消纳能力方面带来的收益将是非常可观的。此外,考虑到SNOP技术在降低网损方面的应用,SNOP技术总体上可以取得良好的经济效益。未来随着换流器设备的发展成熟及成本不断下降,基于SNOP的柔性配电网具有广阔的发展前景。下一步考虑对多端含储能SNOP在柔性配电网中的规划和运行优化问题进行研究。2 模型求解方法
3 算例分析
3.1 原始数据
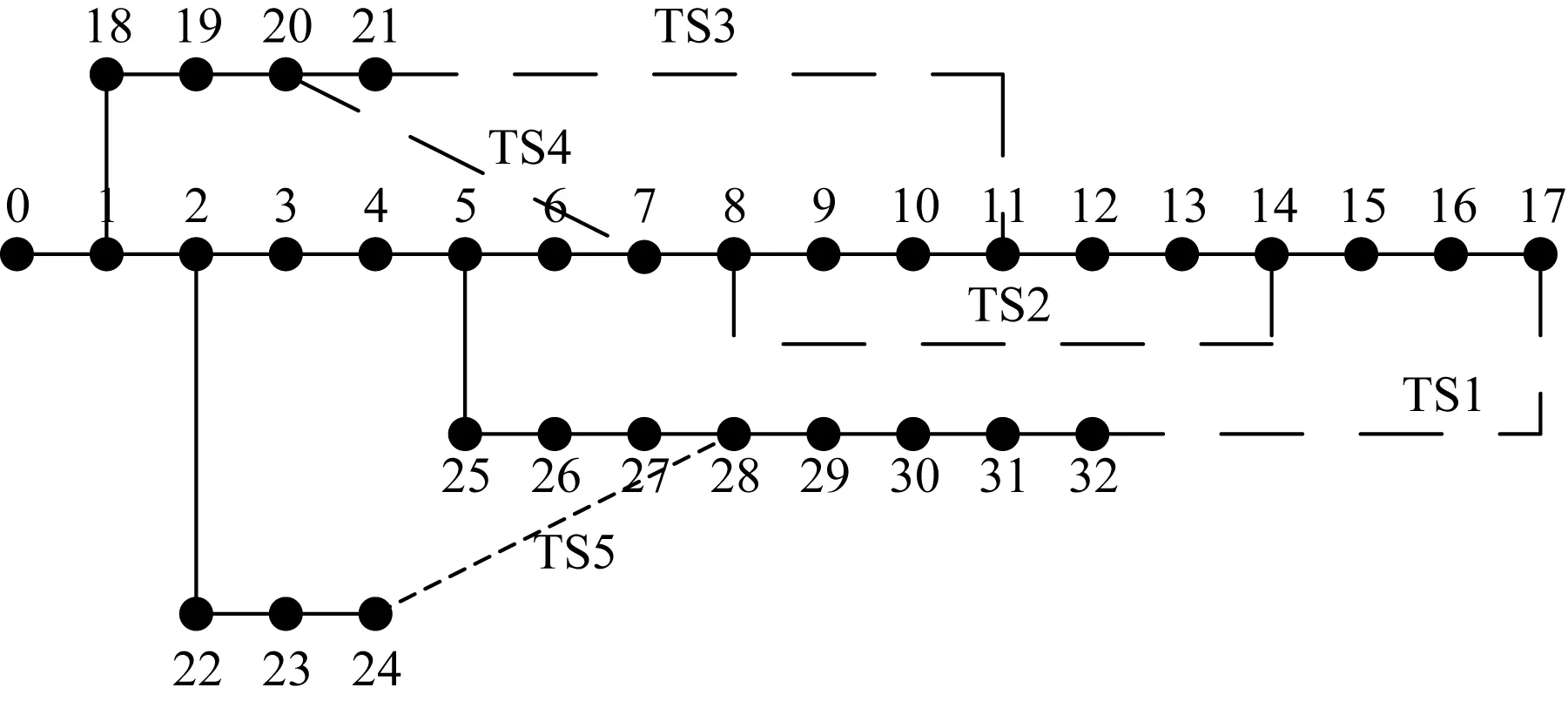
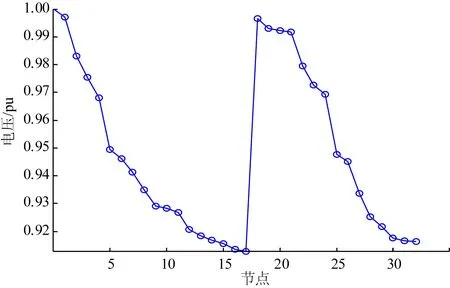
3.2 无SNOP配电网DG单点准入容量计算
Table1AllowableDGcapacityatdifferentbuses
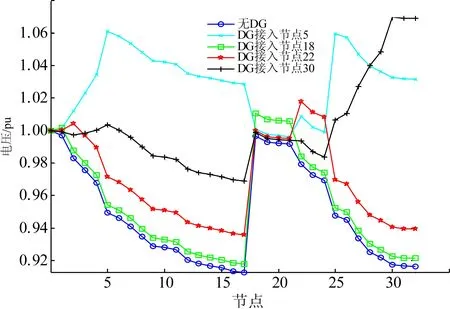
3.3 SNOP对指定节点DG准入容量提升分析
Table2PromotionofSNOPtotheallowableDGpenetrationcapacityinmulti-bus/single-freederscenario
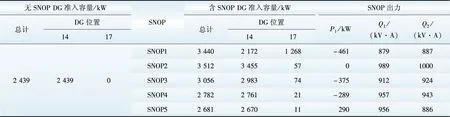

3.4 SNOP容量灵敏度分析


3.5 FDN中DG极限准入容量计算
Table5OptimizationmethodwithfreesitesofDGs
4 结 论
