基于下垂控制的逆变器参数对微电网稳定性的影响研究
2018-08-08梁海峰董玥郑灿
梁海峰,董玥,郑灿
(华北电力大学电力工程系,河北省保定市 071003)
0 引 言
一次能源日益枯竭的现状推动了以新能源发电技术为核心的能源革命的全面展开[1]。但由于清洁能源的不确定性和差异性,将会给传统电网的可靠性和稳定性造成冲击。在当前技术环境下,微电网是新能源发电设备并网最为有效的手段之一[2]。为了提高此类能源的市场占额,含分布式电源的微电网稳定运行至关重要。
事实上,微电网中分布式电源设备的输出形式多为直流电形式或非工频交流电形式,多采用具有开关全控性的电压源换流器[3](voltage source converter,VSC)转换为工频交流电向网内输送能量。基于此,对微电网中电源的协调控制技术研究应集中在对各VSC的控制策略上。微电网VSC之间的协调控制主要分为主从控制和对等控制。与主从控制相比,对等控制更易于实现分布式电源的“即插即用”需要,同时省去了大量通信系统的成本投入[4]。而且逆变器采用对等控制策略有利于微电网在孤岛和并网2种模式间进行切换。特别是对等控制范畴中的下垂控制策略,当其应用于微型燃机、燃料电池等具有电压和频率支撑作用的分布式电源时,不仅可以解决电源间的协调运行问题,而且可以实现功率在电源间的合理分配[5]。因此,微电网的下垂控制策略得到了学术界广泛关注和研究。
采用下垂控制策略的微电网在孤岛模式下不存在主平衡节点,系统电压和频率完全依赖于分布式电源的分散调节[6],稳定性差成为该控制策略的最大瓶颈,因此该控制策略的稳定性研究对微电网的安全运行有着重大意义[7]。围绕下垂控制的稳定性分析,不少专家和学者做过大量研究。文献[8]立足于微电网架构和网络拓扑,建立了微电网多电源并联结构中下垂控制的小信号状态空间模型,并利用该模型求取了微电网在不同稳态工作点的系统特征值,评估了系统稳定性的变化趋势,同时定性分析了负荷阻抗变化、线路变化对于小信号频率稳定性的影响。文献[9-10]在建立网络小信号模型的基础上,分析了由下垂系数连续变化引起的模型特征值变化,尤其是文献[9]还验证了下垂控制环节中添加有功功率前馈环节对改善稳定性的作用。但是上述文献的分析更倾向于网络层面的稳定性分析,对逆变器内在控制结构考虑不足。文献[11-12]对下垂控制策略下逆变器个体的电气结构建模,分析了稳态和暂态工况下有功下垂系数、无功下垂系数和低通滤波器对逆变器输出的影响,但该分析对控制器的机理和结构分析不足。文献[13]结合控制器结构,对功率-电压-电流三环控制进行了分解分析,定性分析了控制器参数对稳定性的影响,提出并验证了引入功率微分项对系统阻尼的增强作用。但是该文献并没有建立完整的逆变器个体控制结构模型,而只局限于局部结构的稳定性研究。文献[14]对电压电流双环控制及输出建立了详细模型,就此模型分析了控制的稳定性,但在分析中对于电流环输出信号和功率之间的关系以及功率反
馈结构研究并不深入,也未进一步研究控制器参数对系统稳定性的影响。
为了更深入研究逆变器对微电网的影响,本文对个体逆变器功率-电压-电流三环控制结构进行建模分析,获得下垂控制策略下逆变器的全结构小信号模型,并从参数角度,定量分析各控制参数在选取不同值时对逆变器输出稳定性的影响。根轨迹法与仿真结果说明该模型下的分析结果满足微电网的稳定性要求。
1 控制对象分析
微电网多电源并联结构中的下垂控制是基于感性线路环境下功率表达式设计的,具体为
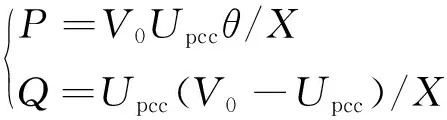
式中:P、Q分别为逆变器输出的有功功率和无功功率;V0、Upcc和θ分别为逆变器输出电压、并联母线电压及两者间的相角差;X为两者间线路电抗。
由式(1)可知,有功功率和功率角呈线性关系,无功功率和输出端电压呈线性关系,因此可以通过P-f和Q-V的关系实现对输出有功功率和无功功率的控制。VSC下垂控制策略通常采用在电压电流双环控制的基础上外加功率下垂控制环,从而构成功率-电压-电流三环控制,如图1所示[15]。
但复杂的结构给稳定性分析带来了较大困难,应对该控制模型进行解耦和简化。图1中电压电流双环控制是一种将电压控制和电流控制进行嵌套的dq0坐标系控制。其中内环电流控制用于实现对交流侧电流波形和相位的直接控制,以实现电流调节的快速性;而外环电压控制用于追踪参考电压,双环解耦控制框图如图2所示[16]。
在该双环控制中,内环电流控制各参量有如下关系[17]。
(2)

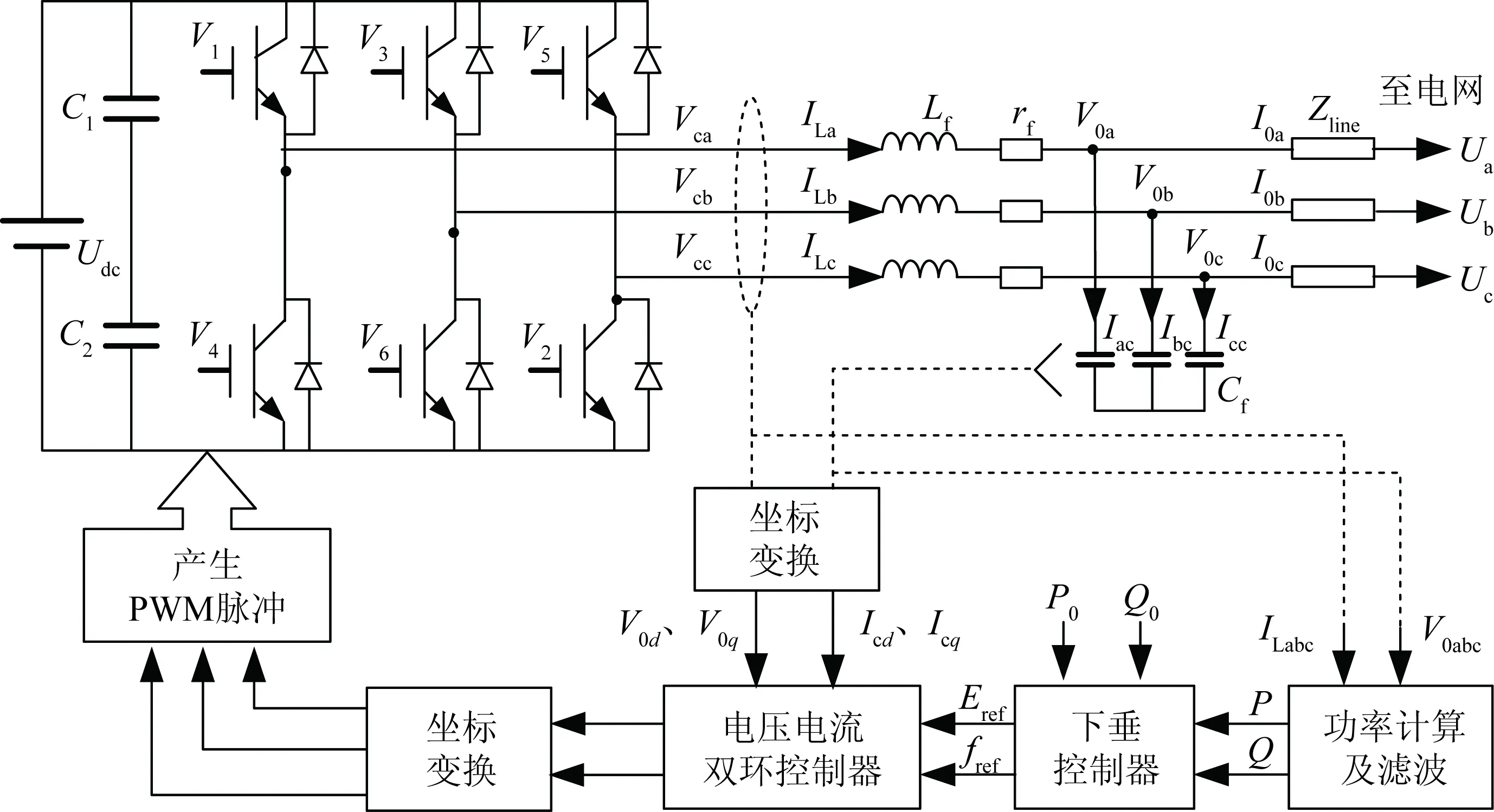
图1 功率-电压-电流三环控制结构Fig.1 Power-voltage-current 3-loop control structure
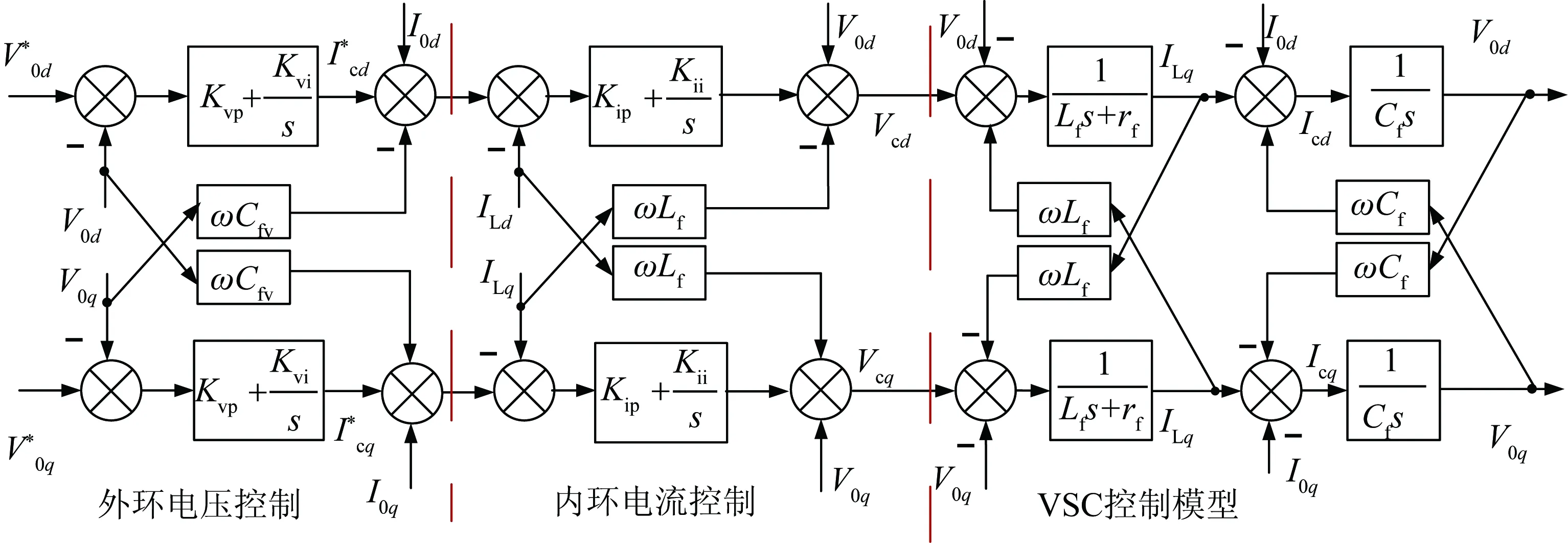
图2 VSC双环解耦控制框图Fig.2 Dual-loop decoupling control diagram of VSC
对VSC逆变器进行电气量分析,关系式为
(3)
式中rf为滤波电感的寄生电阻。将式(3)代入控制式(2)可得
(4)
由式(4)可以看出,采用双环控制结构可以实现dq轴的解耦控制。rf作为寄生电阻,一般数值很小,可以忽略,所以内环电流PI控制中与之对应的积分项也可以忽略。在实践中,为了实现对内环电流参考信号的快速跟踪,一般不采用积分项,而采用简单的P控制代替,即设定Kii=0[18]。
2 小信号控制模型
以上解耦控制中d轴与q轴类似,故电流环控制以q轴为例分析,同时考虑脉冲宽度调制(pulse width modulation,PWM)的调制过程和电流的采样过程,其控制框图如图3所示。
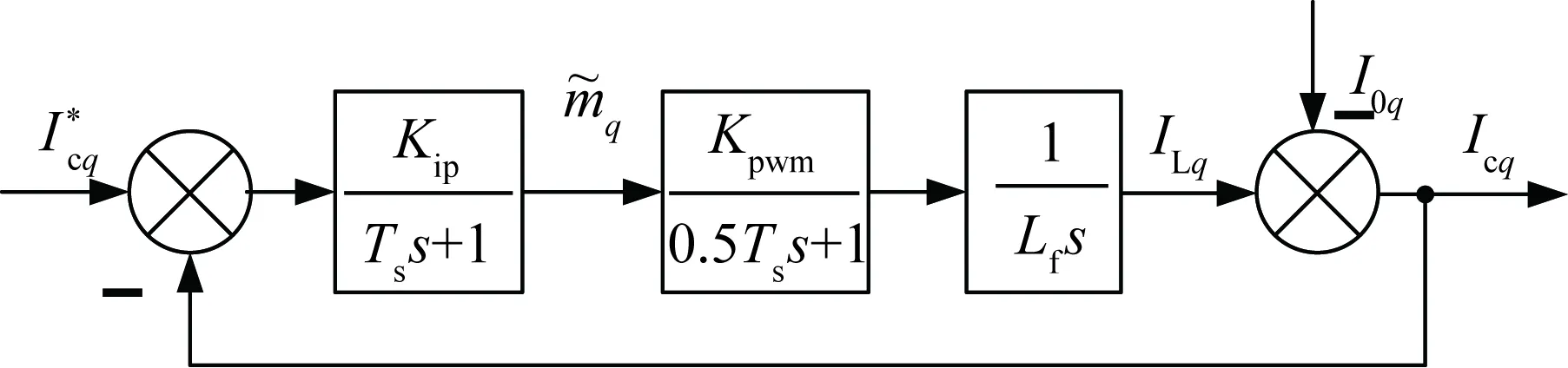
图3 电流环控制结构图Fig.3 Structure diagram of current loop control
图3中:1/(Tss+1)为控制系统采样延迟环节;Ts为系统采样时间常数,当系统开关频率设定为fs=20 kHz时,Ts=1/fs=0.05 ms;1/(0.5Tss+1)为PWM调制器的控制延迟环节;Kpwm为调制器的增益,当直流电压Udc=800 V时,Kpwm=Udc/2=400 V。因Ts数值较小,则对该两项中的延迟环节近似合并为1/(1.5Tss+1)环节[19],则电流环的传递函数为
(5)
电流环开环传递函数为
对Kip进行设计,配置电压控制器的增益,使得控制的截止频率为1/10的开关频率,即有
式中ωx为设计控制截止频率。根据PWM调制器的开关频率为20 kHz,设定LC无源滤波器的电感Lf为1.5 mH,求得Kip≈0.065。
与电流环类似,当控制参数Cfv设置恰当时,电压环可以顺利实现解耦控制,该值可以通过实验方式获得,因与解耦后的控制系统无关,此处不再讨论。电压环d轴与q轴类似,仍以q轴为例分析电压环控制,同时考虑电压的采样过程,其控制框图如图4所示。
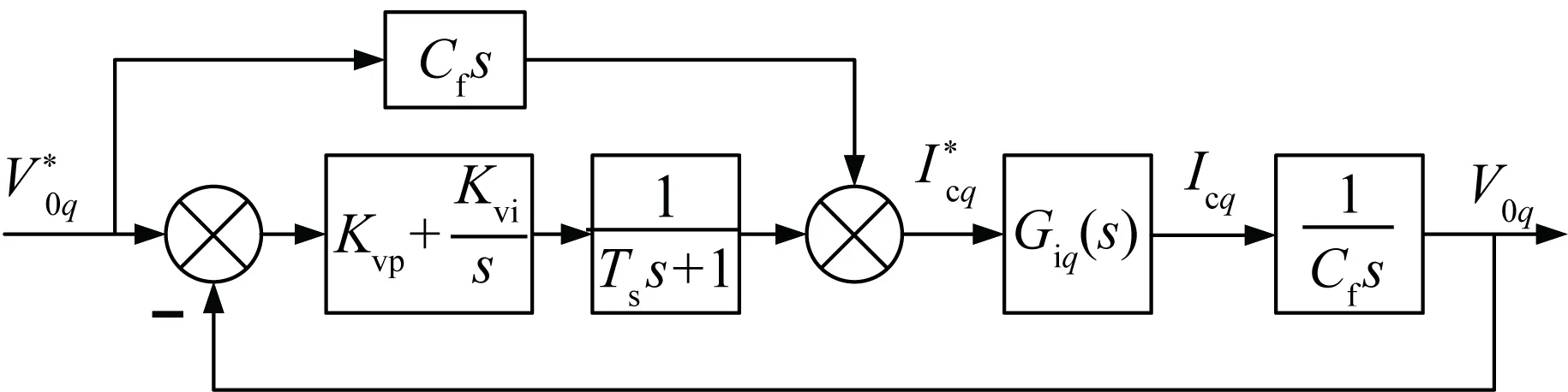
图4 电压环控制结构图Fig.4 Structure diagram of voltage loop control
外环电压控制采用了前馈-反馈混合控制结构,是考虑到电压环处于嵌套结构的外环,控制的响应性较差,添加Cfs前馈环节,有利于提高外环电压控制的调节速度[20]。其中Cf为滤波电容值。该前馈设计是基于VSC物理模型中滤波电感具有以下关系式。
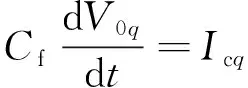
在混合控制结构中,前馈项的引入提高了响应速度,同时不会对反馈调节器的参数整定带来大的影响[21]。因此该处PI参数整定可简化为反馈控制参数确定问题。此结构下电压传递函数为
(9)
式中Kvp、Kvi分别为电压环的比例系数、积分系数。
由式(9)可得到等效开环传递函数为
采用PWM调制的逆变器出口电压会在开关频率处产生大量谐波,一般需要在逆变器出口加装LC无源滤波器以过滤高次谐波。对于LC无源滤波器的设计原则为[22]

式中:fc为滤波器的设计谐振频率;fn为基波频率。本文所研究的系统采用fn=50 Hz,fs=20 kHz,选取fc=1 000 Hz,以滤去该频率附近的谐波。考虑滤波电感上的电压降问题,选取Lf=1.5 mH,求得滤波电容值Cf=16.89 μF。取Cf的值为20 μF,经过校核,满足公式(11)。
在此滤波器参数下进行控制器参数确定。配合电流环的截止频率设计,此处的截止频率仍然选择1 000 Hz。外环PI参数应满足式(12)。
20lg|Gvq0(jωx)|=0
(12)
为兼顾外环控制的稳定性和快速性,预设置Kvp为0.1,求得Kvi=407.65。将所整合参数代入传递函数Gvq(s)的特征方程,有
CfTss3+Cfs2+Giq(s)Kvps+Giq(s)Kvi=0
(13)
利用迭代法求得近似解:S1= -16 075.9,S2,3= -1 809.9±j6 537.6,S4,5=-6 818.7±j8 858.3。特征根均在左半平面,故该控制结构稳定,参数整定合理。
对于功率下垂控制环节,本文在功率静态工作点附近建立线性化小信号模型,分析下垂控制策略的小信号稳定性。小信号模型中,逆变器经线路连入微电网的公共并网点,选定并网点电压为参考电压,即Upcc∠0=Upcc,d+j0,逆变器滤波器输出点电压为V0∠θ=V0d+jV0q。在纯感性Xline的线路环境中,电流可表示为
(14)
根据式(14)可以得出小信号量表达式为

根据dq0坐标系下的有功功率表达式P=V0dI0d+V0qI0q,可得小信号表达式为
P=I0dΔV0d+V0dΔI0d+I0qΔV0q+V0qΔI0q
(16)
针对有功功率小信号模型,假设如下:(1)认为θ值较小,则有V0d>>V0q;(2)正常运行工况下,Upcc,d和V0d数值接近,在感性线路中,I0q≈0并有ΔV0d/V0d<<ΔI0d/I0d。
在工程实践中,低压微电网线路参数并不以感性为主,为使下垂控制更好地应用于工程实践,学者们通过添加“虚拟阻抗”环节保证微电网线路的感性环境,因配置的“虚拟阻抗”并不影响有功功率输出,此处不再展开介绍,只以Xline>>Rline代表“虚拟阻抗”环节的效果[5]。基于上述假设,有功功率的小信号模型可简化为
P≈I0dΔV0d(ΔV0d/V0d+ΔI0d/I0d)≈
V0dΔI0d≈UpccΔV0q/Xline
(17)
结合下垂控制中P=P0-(ω-ω0)/(2πm)的控制原理,相角小信号模型为
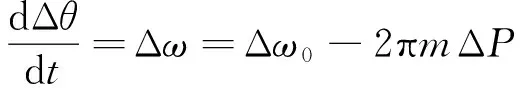
式中Δω0为逆变器设计输出频率的变化量。
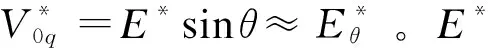
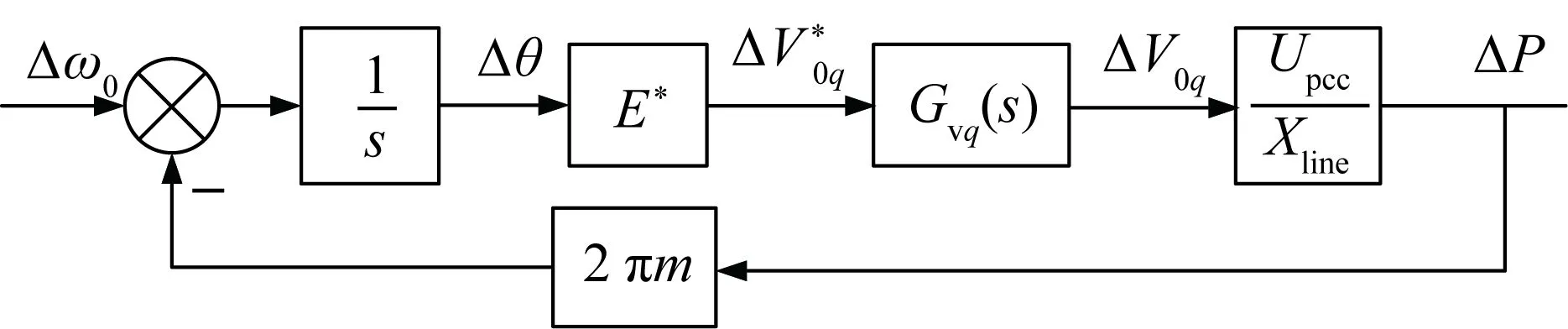
图5 有功功率下垂控制结构Fig.5 Structure of active power droop control
有功功率下垂控制的开环传递函数为
(19)
式(19)即为逆变器有功功率-电压-电流三环全结构控制模型开环传递函数。利用相同的建模思想可建立无功功率-电压-电流全结构传递函数,本文不再重复论述。基于对所得到的传递函数的深入分析,不仅可以有效地判断下垂控制系统的稳定性,更可以优化配置控制器参数,合理选择滤波器。从更深层次说,该传递函数的确定及分析将为下垂控制的设计提供理论依据,为多逆变器并联系统的协调控制稳定性提供一种分析方法。
3 基于案例的理论分析
当所接入网络的电压等级为220 V时,E*≈Upcc=220×1.414 V =311 V;下垂系数取0.000 2,即在[49.5,50.5]Hz的频率许可范围内,逆变器的输出波动在5 kW以内;纯电感线路取Xline为0.5 Ω。研究Gdroop(s)=ΔP/Δω0闭环传递函数的特征方程D(s)=1+Gdroop0(s)=0的特征根轨迹。
3.1 有功下垂系数对稳定性影响的理论分析
以有功下垂系数为开环增益,对应的开环传递函数可表示为
(20)
观察开环增益为K=m的根轨迹,判断有功下垂系数对稳定性的影响,根轨迹如图6所示。
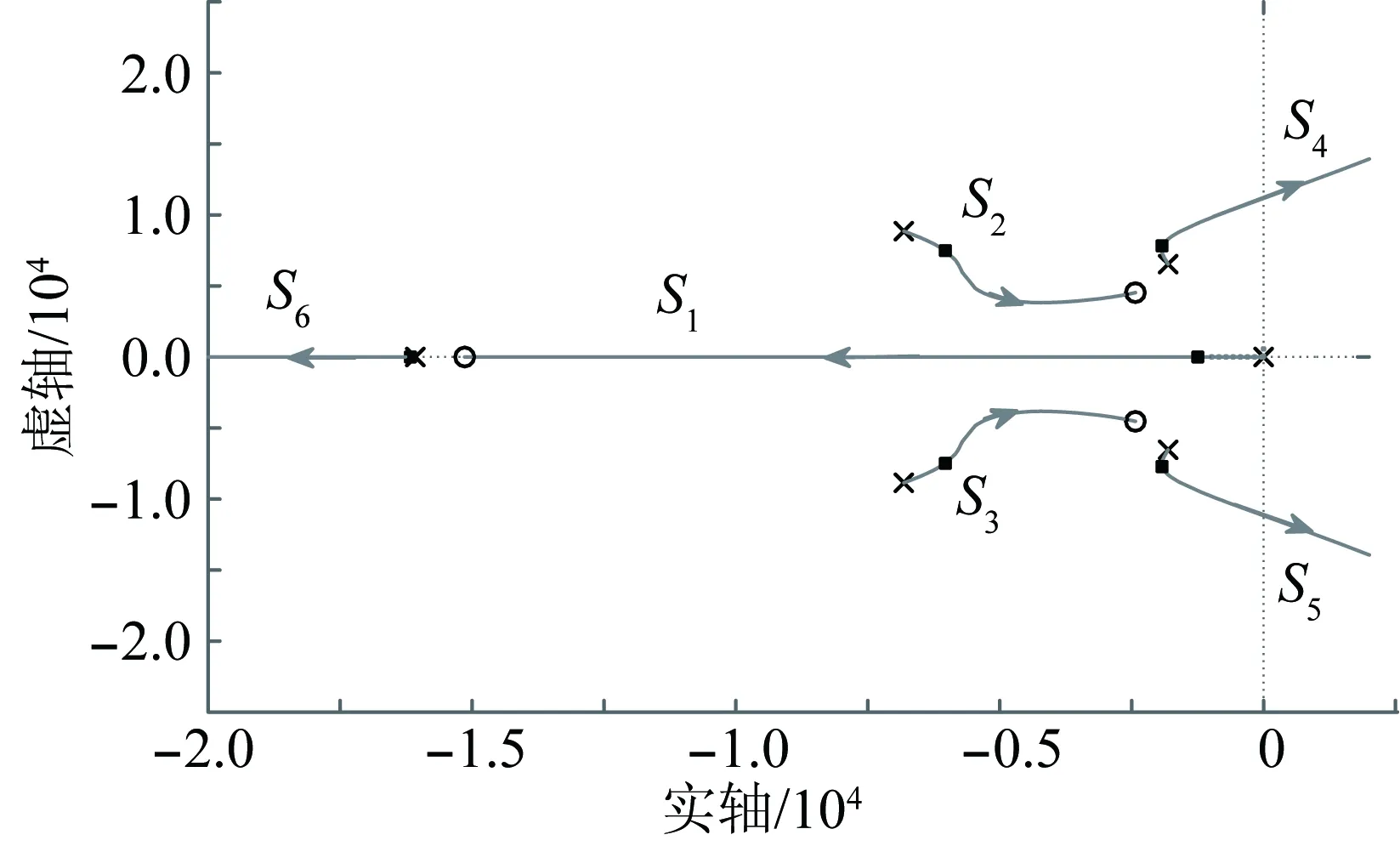
图6 有功功率下垂系数作为增益的根轨迹Fig.6 Root locus of active power droop coefficient
当m从0向+∞变化时,6条根轨迹线变化如下:S2、S3、S6这3条根轨迹线位于负半平面且保持远离虚轴,其变化对稳定性影响不大,为非主导根轨迹;随着m增大,S1从原点出发,沿实轴向负无穷运动,S4、S5这2条根轨迹线从负半平面上靠近虚轴的点出发,先向负平面运动,后向正半平面运动,在某点进入正半平面。此3条根轨迹线对系统的稳定性影响较大,视为主导根轨迹线。数据分析可知,S4、S5这2条根轨迹线方向改变点所对应的m=0.001 02,穿越虚轴对应的m=0.004 96。
综上分析,当m从0增大到0.001 02时,S1、S4、S5均向左运动,系统的稳定性显著增加;当m从0.001 02增大到0.004 96时,S1继续向左运动,S4、S5向右运动且逐渐远离实轴,系统的惯性降低,响应将有较大的振荡过程,稳态性能变差;当m>0.004 96时,S4、S5进入正半平面,可判定系统不稳定。为保证系统稳定,下垂系数可选范围为(0,0.004 96)。此分析为下垂系数的确定在容量-允许波动频率规则之外,又提供了一条辅助选定依据。
3.2 电压环积分系数对稳定性影响的理论分析
根据广义根轨迹分析法,其等效开环传递函数可表示为
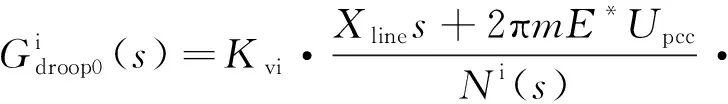
(21)
Ni(s)=CfTsXlines4+
[CfXline+2πCfTsmE*UpccGiq(s)]s3+
(KvpXline+2πCfmE*Upcc)Giq(s)s2+
KvpmE*UpccGiq(s)s
(22)
据此可分析开环增益K=Kvi时,电压环控制器积分系数对稳定性的影响。由公式(22)可知,分母Ni(s)是6阶多项式,但是存在1对零极点P=-242.919和Z=-243.085满足对消条件,根轨迹可简化为5条分支,如图7所示。
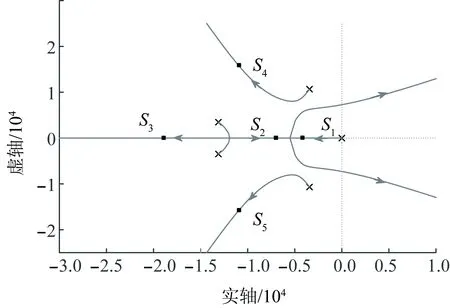
图7 电压环积分系数作为增益的根轨迹Fig.7 Root locus of voltage loop integral coefficient
当Kvi从0向+∞变化时,距离虚轴最近的S1沿实轴向负无穷运动,其余各分支均距离虚轴较远。由于主导根S1不断向负方向移动,系统的稳定性在不断增强。当Kvi增大到197.0,S1和沿实轴向正方向运动的S2轨迹线汇合,之后两者虚部开始增大,同时向正半平面移动,稳定性逐渐变差,同时系统响应的振荡特征开始增强。直到Kvi增大到643.7,两根进入正半平面,系统不再稳定。
综上分析,在Kvi从0增大到643.7的过程中,系统的稳定性先是不断增强,然后逐渐降低;当Kvi超过643.7后,系统失去稳定。
3.3 电压环比例系数对稳定性影响的理论分析
利用广义根轨迹分析法,其开环传递函数为
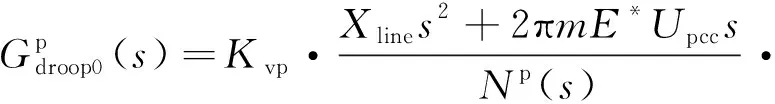
(23)
Np(s)=CfTsXlines4+
[CfXline+2πCfTsmE*UpccGiq(s)]s3+
2πCfmE*UpccGiq(s)s2+KviXlineGiq(s)s+
2πKvimE*UpccGiq(s)
(24)
据开环传递函数分析开环增益为K=Kvp时,电压环控制器比例系数对稳定性的影响。由公式(24)可知,分母Np(s)是6阶多项式,存在P=-243.097和Z=-243.087零极点对消情况,则根轨迹也可简化为5条分支,如图8所示。
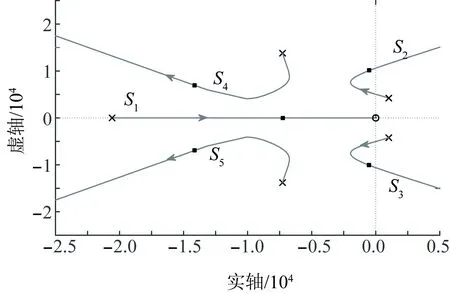
图8 电压环比例系数作为增益的根轨迹Fig.8 Root locus of voltage loop proportional coefficient
当Kvp从0向+∞变化时,距离虚轴最近的S2和S3自正半平面向虚轴运动,此时系统处于不稳定状态;当Kvp增大到0.050 9时,S2和S3进入负半平面,并继续向实轴负半轴方向移动,此时系统稳定且抗扰动能力不断增强;当Kvp增大到0.109 2时,S2和S3运动方向翻转,开始向实轴正方向运动,稳定性不断减弱,并最终在Kvp增大到0.185 0后重新回到正半平面,系统变得不稳定。在以上过程中,S1、S4和S5始终远离虚轴,对稳定性影响较小,可看作非主导根。
综上分析,Kvp<0.185 0时,S2和S3为系统的主导根,且增大过程中存在2次虚轴穿越现象,所以该参数选取对系统稳定有较大影响,保证系统稳定的Kvp取值范围为(0.050 9,0.185 0)。
根据3.2和3.3节的分析可知,对下垂控制三环全结构传递函数进行数值分析,可以为该结构控制器参数的核算及校正提供更加准确的参考,并推动基于多逆变器并联微电网稳定性的系统控制结构设计实践。
4 仿真验证
为着重研究下垂控制参数的影响,利用仿真软件MATLAB/Simulink搭建简易的“两源两荷”孤岛微电网系统,如图9所示。其中,两电源均采用下垂控制策略,并采用不同的下垂系数,以验证下垂控制在功率按容量分配方面的可行性,并假设微网中负荷均为有功负荷。
其具体的参数设置为:(1)负荷配置为Pload,1=10 kW、Pload,2=5 kW;(2)PWM配置为fs=20 kHz,Ts=1/fs=0.05 ms;(3)电压等级为Upcc=220 V、Udc=800 V、Kpwm=400;(4)滤波器及线路参数为Lf1=Lf2=1.5 mH、Cf1=Cf2=20 μF、Xline1=Xline2=0.5 Ω。
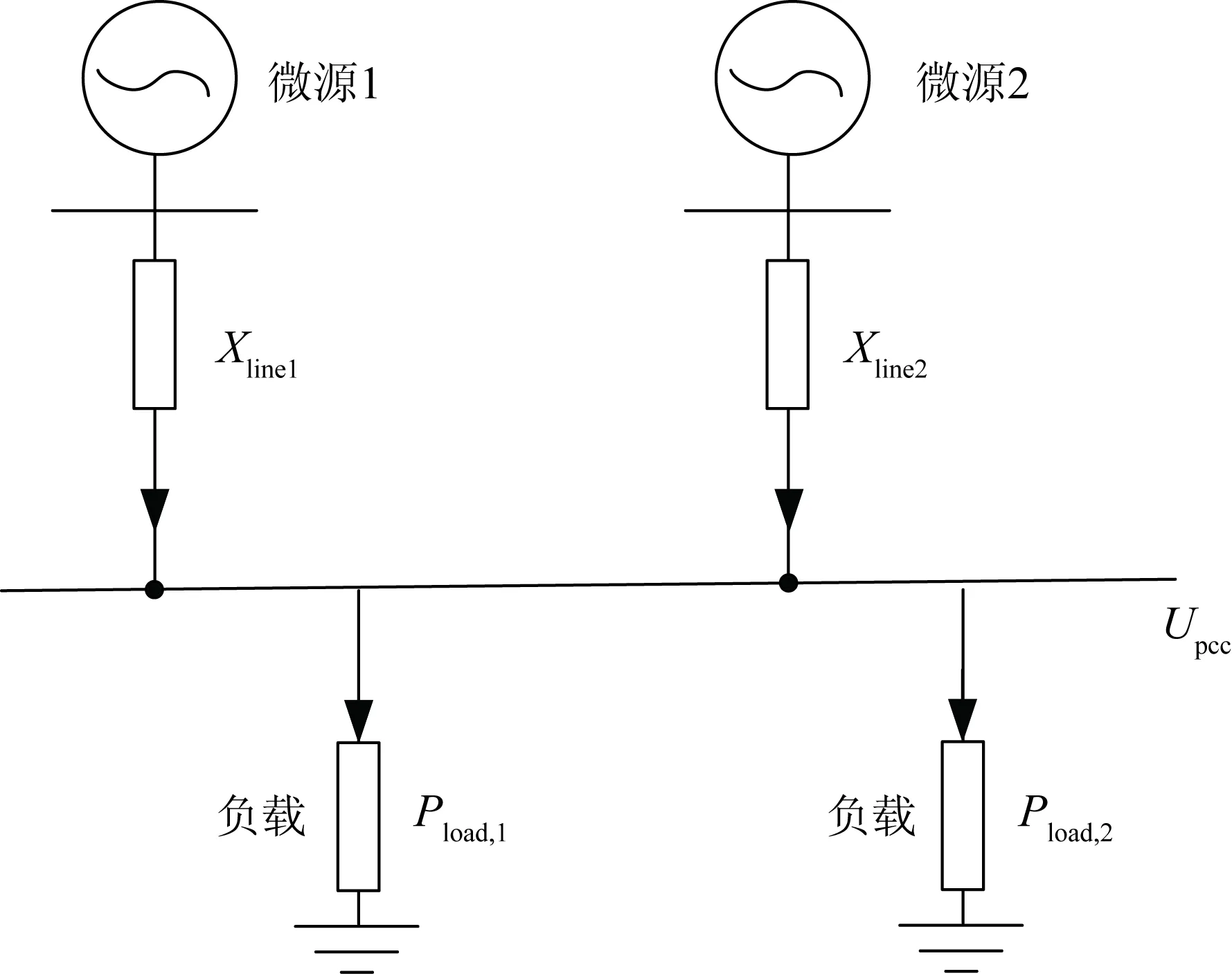
图9 微电网孤岛模式下的简易系统模型Fig.9 Simple system model for island microgrid
4.1 有功下垂系数对稳定性的影响
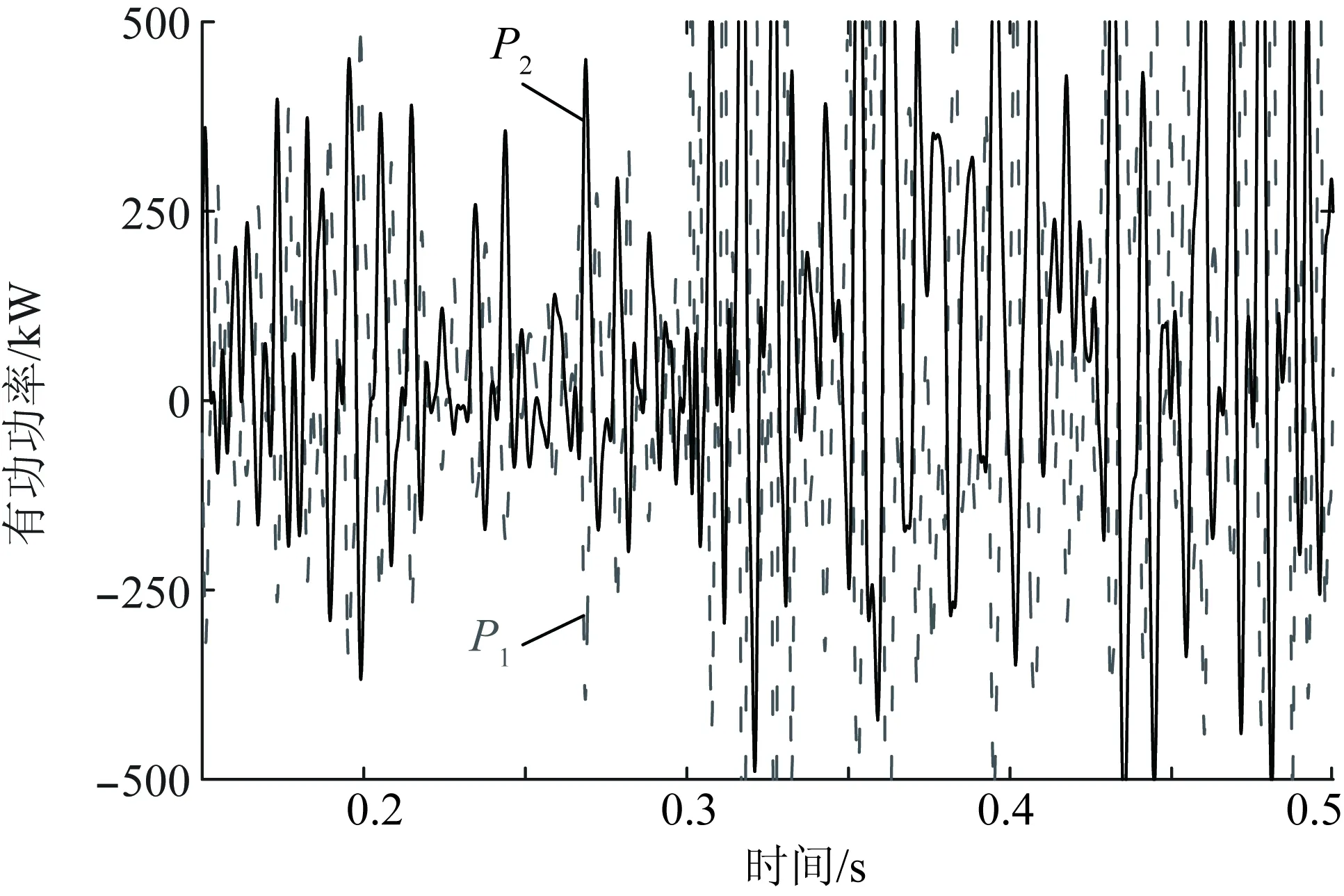
设置两逆变器的电压电流环参数均为Kvp=0.1、Kvi=408.65、Kip=0.065,即按照上文参数选取原则进行参数配置。设置两逆变器下垂系数分别为m1=0.000 4和m2=0.000 2,同时设置两者在50 Hz标准频率下的有功功率输出均为5 kW,则两者P-f下垂曲线分别为P1=5 000- (f-50)/0.000 4,P2=5 000- (f-50)/0.000 2。
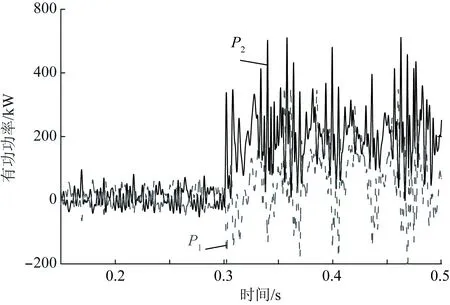
已知m1,m2∈(0,0.004 96),Kvi<643.7,0.050 9 由图10可以看出,当P-f下垂控制系数在理论稳定范围内选取时,负荷突增发生后,各电源基本可以实现按照下垂系数的反比分配功率,从而证明了下垂控制在负荷分配方面的有效性。 为了探究当下垂系数跨越理论稳定限度时系统响应情况,设置仿真与上述相同,但与上述仿真不同之处在于:0.3 s时,不仅负荷突增,同时设置电源1的下垂系数从m1=0.000 40突增为m2=0.006 00>0.004 96,取值不再符合理论稳定性。两电源的有功功率输出如图11所示。由图11可得,此时控制的稳定性已经崩溃,功率出现大幅度增幅振荡。通过图10和图11的对比可证明:依靠下垂控制稳定性模型,探究下垂系数变化对控制系统稳定性的影响,该分析方法具有合理性。 图11 下垂系数超越理论限值时电源功率曲线Fig.11 Active power allocation when droop coefficient out of theoretical limit 设置两逆变器电压电流环控制参数为Kvp=0.1、Kvi=800、Kip=0.065。设置两逆变器下垂系数分别为m1=0.000 4和m2=0.000 2。已知m1,m2∈(0,0.004 96),Kvi>643.7, 0.050 9 由图12可以看出,功率振荡贯穿了整个控制过程,系统未曾达到稳定,尤其是在经过0.3 s处的负荷变化,功率振荡加剧,控制系统呈现出明显的不稳定性。通过对图10和图12的功率曲线的比较可以证明:依靠下垂控制稳定性模型,探究电压环控制器积分系数选取不同值对控制系统稳定性的影响,该分析方法具有合理性。 在4.2节的基础上改变Kvp和Kvi的值,令Kvp=0.3,Kvi=408.65。已知m1,m2∈(0, 0.004 96),Kvi<643.7,Kvp>0.185 0,Kvp理论上不再符合系统稳定条件。设计仿真条件为:开始时,两电源向Pload,1供电,在0.3 s时,Pload,2投入,负荷突增。所对应的两电源的有功功率输出如图13所示。由图13可以看出,整个控制过程都伴随着或多或少的功率振荡,系统稳定性不足,尤其是在经过0.3 s处的负荷变化,功率振荡骤然加剧,在该控制结构下,系统无法达到稳定。通过图10和图13的功率曲线的比较可证明:依靠下垂控制稳定性模型,探究电压环控制器比例系数选取不同值对系统稳定性的影响,该分析方法具有合理性。 图12 电压环积分系数超越理论限值时电源功率曲线Fig.12 Active power allocation when voltage loop integral coefficient out of theoretical limit 图13 电压环比例系数超越理论限值时电源功率曲线Fig.13 Active power allocation when voltage loop proportional coefficient out of theoretical limit 本文着眼于微电网下垂控制策略中逆变器个体的控制稳定性,就功率-电压-电流三环下垂控制结构进行了深入研究,建立了关于逆变器的全结构小信号传递函数模型。结合具体案例,定量分析了设置不同的下垂系数、电压环控制器积分系数、比例系数对逆变器控制系统产生的影响,给出了保证系统理论稳定的三者选取范围。在理论分析基础上,通过仿真分析,验证了所建立的小信号模型的合理性及该模型在控制稳定性分析方面的有效性。 除文中所提及的案例外,为验证该模型的普适性,本研究利用所建立的模型进行大量的案例分析,涵盖不同的电压等级和容量参数,得到以下结论。 (1)随着有功下垂系数的增大,系统的稳定性趋于减弱,直至不稳定,从电气量上解释,即单位功率增减对应的频率变动值不宜过大,否则微小的功率波动将引起系统频率崩溃。 (2)随着电压环控制器积分系数的增大,系统稳定性先增强后减弱,直至不稳定,这是因为在控制中积分项的添加可以提高系统的静态稳定性,但积分项过大造成电压环响应迟缓而不再适用于对快速波动电压的调节。 (3)电压环控制器比例系数的选取对控制系统稳定性影响很大。只有在适当范围内选取比例系数,通过与积分系数配合,才能兼顾电压控制的快速性和稳定性。本文的研究为比例系数选取范围提供参考依据。 综上所述,本文所建立的小信号模型是对逆变器下垂控制的全结构简化而得到的,不仅考虑了输出端与滤波器及并网点的电气关系,也深入研究了控制系统的内在机理。此外,本文中所用两源模型简化了线路参数和负荷参数,对于较复杂的交流微电网将进一步研究。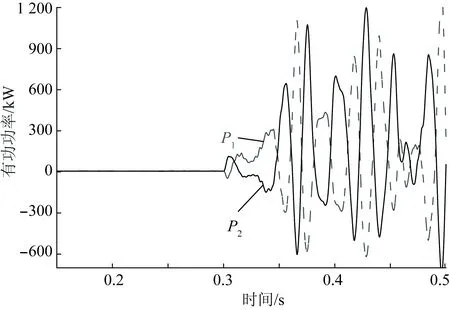
4.2 电压环积分系数对稳定性的影响
4.3 电压环比例系数对稳定性的影响
5 结 论
