基于离散傅里叶变换的主动配电网混合储能容量优化配置
2018-08-08钟国彬吴涛曾杰谢开贵王超胡博
钟国彬,吴涛,曾杰,谢开贵,王超,胡博
(1.广东电网有限责任公司电力科学研究院,广州市 510080;2.输配电装备及系统安全与新技术国家重点实验室(重庆大学),重庆市 400044)
0 引 言
近年来,我国风电、光伏发展迅猛,装机容量跃居世界第一,但可再生能源的随机性和波动性对其高比例接入配电网提出了巨大的挑战。储能技术和主动配电网的发展为实现可再生能源的高比例接入提供了可能[1-3]。储能在功率调节方面具有显著优势,可提高可再生能源渗透率[4-5]、改善网络潮流分布[6]等。合理配置储能是优化主动配电网运行的关键,可有助于平抑可再生能源间歇性波动,保证配电网电能质量和供电可靠性,提升系统经济性。
文献[7]提出一种规划-运行双层协调优化模型,在规划层面考虑线路改造和新建、储能和可再生能源的优化配置,在运行层面优化储能和可再生能源调度,实现主动配电网的投资优化。文献[3]提出一种基于目标机会约束规划的储能容量配置方法以提高主动配电网灵活性,但能量型储能充放电时间长、寿命短且功率密度低[8],仅配置单一类型储能易降低系统经济性。
功率型储能功率密度高、响应快速、使用寿命长,将其与能量型储能组成混合储能系统可提升储能系统经济性[9-10]。文献[9]基于离散傅里叶分解,以储能投资成本、运维成本、可靠性费用之和最小化为目标函数,建立孤岛型微电网混合储能优化配置模型,优化混合储能容量。文献[10]以平滑风电出力波动为目标,提出一种基于约束规划的混合储能系统容量配置方法,协调优化电能质量和系统经济性。
频繁、深度充放电将会严重影响铅酸蓄电池等能量型储能使用寿命[8,11]。忽略寿命损耗会导致实际投资成本显著增加。因此,在优化配置储能时,须考虑储能设备寿命损耗的影响。同时,主动配电网可作为利益整体,与上级电网交易电能[12],优化混合储能系统充放电状态,减少寿命损耗,提升储能系统经济性。
混合储能系统在运行过程中,储能单元间的功率分配直接影响混合储能系统的容量优化配置结果,常用的功率分配方法包括低通滤波[13]、高通滤波[14]、滑动平均滤波[15]等。滤波器在滤波的过程中会产生延迟,使储能优化容量产生误差[11]。离散傅里叶变换(discrete Fourier transform,DFT)及离散傅里叶逆变换(inverse discrete Fourier transform,IDFT)是适用于离散时间序列的数字信号处理方法,具有运算速度快,数据变换无损等特点[16]。此方法可实现混合储能系统功率在各储能单元间的优化分配。
鉴于此,本文考虑寿命损耗和优化运行对储能容量配置的影响,提出一种基于离散傅里叶变换的主动配电网混合储能容量优化配置模型。该模型在规划层面确定混合储能容量配置方案;在运行层面通过模拟运行,并利用离散傅里叶变换确定混合储能系统运行方案。通过计算能量型储能的寿命损耗,同时考虑分时电价,计及配电网与上级电网的电能交易,优化混合储能系统运行,实现规划-运行协同优化。
1 考虑混合储能的主动配电网系统模型
主动配电网可以对局部的分布式能源设备进行主动控制和管理[1]。本文重点分析含风电、光伏和混合储能的主动配电网。须说明的是,在本文中,主动配电网的“主动”主要体现在将配电网作为利益整体,与上级电网交易电能,优化运行混合储能系统。
1.1 电源模型
1.1.1风电和光伏机组
研究表明,可用分段函数表征风速和风电机组输出功率之间的转换关系,光伏机组出力主要取决于太阳辐照度[17],具体模型在此不再赘述。
1.1.2混合储能系统
混合储能系统的运行状态可用荷电状态(state of charge, SOC)表征,满足如下关系:
(1)

1.2 混合储能系统特点及结构
混合储能系统由能量型储能和功率型储能组成。能量型储能容量密度大,成本低,但充放电功率小,寿命易受充放电次数和深度影响,因此适宜承担波动幅度大、周期长的低频功率[18]。功率型储能功率密度大,可频繁充放电,但容量有限,可主要承担波动幅度小、周期短的高频功率[19]。
本文采用铅酸蓄电池和超级电容器组成混合储能系统,如图1所示。
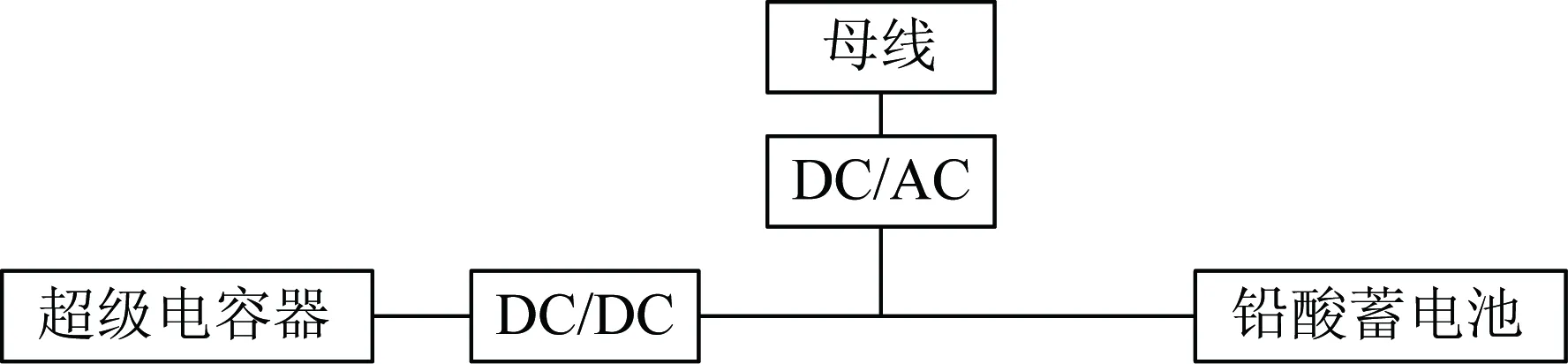
图1 混合储能系统结构Fig.1 System structure of HESS
2 基于离散傅里叶变换的混合储能系统功率分配
混合储能系统运行时,最重要的环节是在不同储能单元间分配功率。本文采用离散傅里叶变换实现混合储能系统功率在各储能单元间的最优分配。
2.1 离散傅里叶分解
离散傅里叶变换及其逆变换可将一个信号进行时域-频域间的相互转换,实现信号分解[16]:
X(k)=DFT(x(n))=
x(n)=IDFT(X(k))=
式中:X(k)、x(n)分别为频域信号和时域信号的主值序列;DFT(·)、IDFT(·)分别为离散傅里叶变换和逆变换函数;k为不同频段的序列数。
2.2 混合储能系统功率分配策略
混合储能系统充放电功率可看成是采样周期为Ts,采样点数为N的离散时间序列,根据离散傅里叶变换,可将其进行分解。
将混合储能系统充放电功率代入式(2)可计算出混合储能系统的幅频序列XHESS(k)。根据DFT性质可知,XHESS(k)与以奈奎斯特频率fk=fs/2为对称轴,两侧对称的复序列互为共轭[16],仅需分析前半部分即可,其中采样频率fs=1/Ts。进一步地,XHESS(k)可表示为
0≤k≤N-1
(4)
将上式在某一点k=n处切断,同时在k=N-n处也设置一分段点,n即为频率分段点。n的取值范围为[0,N/2],其中[0,n]为低频区段,[n+1,N/2]为高频区段。将低频和高频分离,并进行补零操作,可得下式:
XHigh(k)={0,…,0,X(n-1),…,
X(N-n-1),0,…,0}
(6)
式中XLow(k)、XHigh(k)分别为混合储能系统充放电功率的低频分量和高频分量。
将式(5)、(6)分别代入式(3)可得混合储能系统的低频功率和高频功率:
(7)
(8)
式中PLow(t)、PHigh(t)分别为混合储能系统的低频功率和高频功率。
通过式(2)— (8),可将混合储能系统充放电功率进行优化分解。由上述分解过程可知,分段点n的选择将会影响混合储能系统功率在各储能单元间的分配,进而影响储能的运行状态,使得混合储能系统的投资运行成本产生变化。通过枚举,可计算不同分段点对应的混合储能系统投资运行成本。在所有优化配置方案中,成本最小时对应的分段点为最优频率分段点,此时的混合储能系统功率在各储能单元间实现最优分配。
3 基于离散傅里叶变换的主动配电网混合储能系统容量优化配置模型
3.1 模型目标函数
本文考虑混合储能系统的投资运行成本,并以整个配电网为市场参与者,计及其与上级电网的电能交易成本,优化配置功率型储能和能量型储能的容量和功率,目标函数为
minf=Ic+Ec
(9)
式中:Ic为混合储能系统投资运行成本;Ec为配电网与上级电网的电能交易成本。
(1)投资运行成本。
通过模拟运行计算储能的使用寿命,利用等年值将其反映在混合储能系统的投资运行成本中:
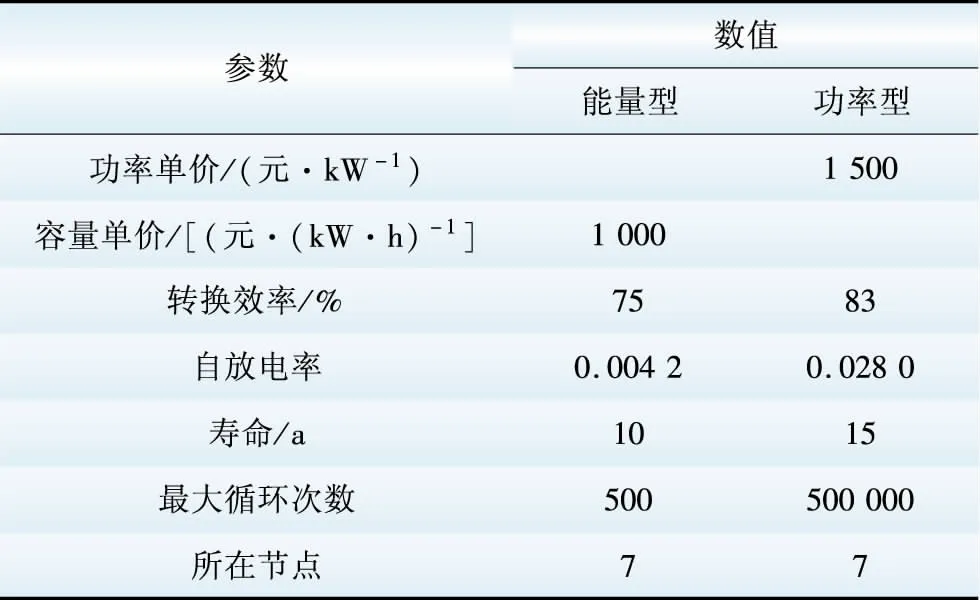
式中:NHESS为混合储能系统储能元件种类数;Ci为储能i的投资运行成本;γ为年利率;λEi、λPi分别为容量单价和功率单价;αi、βi分别为储能i的容量系数和功率系数,由储能特性决定;Pi、Ei分别为储能i的额定功率和容量;Li为储能i的使用寿命,与储能的运行工况相关,具体计算过程详见3.3节。
3.2 模型约束条件
3.2.1功率平衡约束

(11)
PHESS(t)=Penergy-type(t)+Ppower-type(t)
(12)
式中:PS(t)为t时刻的电网注入功率;PL(t)为t时刻的负荷;PHESS(t)为t时刻混合储能系统的充放电功率;PWind(t,i)为t时刻风电机组i的输出功率;PPv(t,j)为t时刻光伏机组j的输出功率;Penergy-type(t)为t时刻能量型储能电网端功率;Ppower-type(t)为t时刻功率型储能的电网端功率;Nw、Ns分别为风电机组和光伏机组数目。
3.2.2储能充放电功率约束
(13)
式中PEi(t)为t时刻储能i的充放电功率。
3.2.3放电倍率约束
(14)

3.2.4储能SOC约束
(15)

3.2.5线路功率约束
(16)

3.2.6倒送功率约束
-0.6Psubstation≤PS(t)≤Psubstation
(17)
式中Psubstation为变压器额定容量。
3.3 混合储能系统寿命损耗成本
能量型储能的等效循环次数与充放电深度(depth of discharge, DoD)相关,根据充放电深度和等效循环次数关系表,可测算能量型储能的等效循环寿命。本文采用切比雪夫多项式[20]拟合曲线:
NESS=A0+A1R+A2R2+…+A8R8
(18)
式中:NESS为充放电深度R对应的等效循环次数;Ai为多项式系数。
采用雨流计数法[21-22]与式(18)可计算能量型储能在充放电深度R下对应的等效循环次数。在调度周期T内,能量型储能的寿命损耗Lloss为
(19)
式中:NESS(R,i)为第i次充放电循环对应的等效循环次数;Nenergy-type为运行周期内能量型储能的完整充放电次数。
基于式(19)可以计算出一个调度周期内的能量型储能的寿命损耗,则其实际运行寿命为
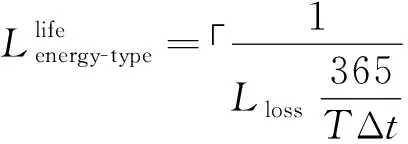
(20)
根据实际运行特点,本文认为功率型储能的实际使用寿命等于其理论寿命。
3.4 电能交易成本
在市场环境下,主动配电网可作为利益整体,参与市场竞争,与上级电网进行电能交易[12],优化混合储能系统的充放电状态,提升储能系统经济性。本文考虑市场环境下的分时电价机制,计算配电网与上级电网的电能交易成本Ec:
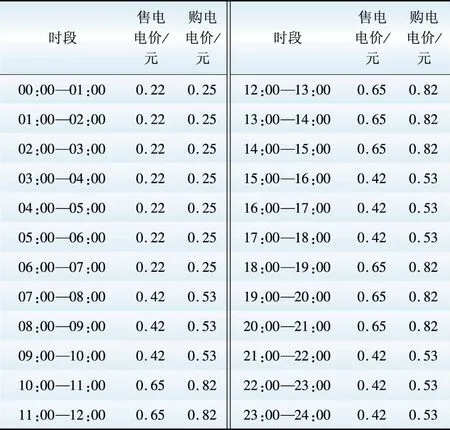
(21)
(22)
式中:C(t)为t时段配电网与上级电网交易电价;C+(t)、C-(t)分别为t时段配电网的购电电价和售电电价;T为总时段数。
电价波动曲线如附录图A1所示。
3.5 模型求解算法流程
本文所建立的主动配电网混合储能容量优化配置模型具有非线性、高维度、多极值等特点,传统数学优化方法难以适用,因此,宜采用智能优化算法。本文将粒子群算法与遗传算法相结合,提高算法的局部和全局搜索能力。算法流程如附录图A2所示。
4 算例分析
4.1 算例参数
本文以改进的IEEE 14节点为例进行算例分析,采用我国华南地区某系统实际运行数据,采样时间间隔Δt=15 min。系统参数详见附录A。系统峰值负荷和主变容量均为10 MW,年利率设为6.7%,储能元件荷电状态SOC上、下限分别为0.9和0.1。铅酸蓄电池和超级电容器的放电倍率分别为0.5和6.0,其详细参数见表1。
表1混合储能系统参数
Table1ParametersofHESS

4.2 结果分析
4.2.1频率分断点对混合储能系统容量配置成本的影响
本节分析频率分段点对混合储能系统容量配置成本的影响。混合储能系统总成本-频率分段点关系如图2所示。
图2中,随着频率分段点不断增大,混合储能系统成本先降后增,频率分段点为13时,混合储能系统容量配置成本达到最低。
当频率分段点较小时,功率型储能须平抑更多功率,因此要配置更大功率的功率型储能。由于功率型储能成本高,导致混合储能系统整体成本也较高。频率分段点取值较大时,能量型储能为主要部分,功率型储能主要用于平抑波动频率高,幅值低的功率。能量型储能须频繁充放电,且充放电深度也有所增加,其实际使用寿命会大幅减少,增加了投资运行成本。
由图2可知,混合储能系统的投资运行成本与频率分段点紧密相关,成本最少时所对应的频率分段点即为最优分段点。

图2 总成本-频率分段点关系图Fig.2 Relationship between total cost and frequency segment point
4.2.2电能交易对混合储能系统配置结果的影响
为分析电能交易和分时电价对混合储能系统配置结果的影响,设立以下3种情形:(1)不考虑电能交易;(2)考虑电能交易但不考虑分时电价;(3)同时考虑电能交易和分时电价。计算结果见表2。
表2电能交易对优化结果的影响
Table2Impactsofenergytransactiononoptimizationresults

主动配电网可与上级电网进行互动,主动管理配电网中的储能设备等分布式电源,优化潮流,进而优化储能设备的充放电状态。情形1至情形3可视为配电网由“被动”向“主动”的转变。从表2中优化结果可知,情形3的混合储能系统成本最低,仅为情形1的一半,这是由于情形1无法优化管理配电网中的储能设备,只有配置更大容量的储能设备才可满足约束。与情形2相比,情形3的储能系统成本和电能交易成本也显著减少,因引入分时电价机制,主动配电网的“主动”性更明显,潮流优化作用更显著,不仅降低了混合储能系统容量配置规模,也延长了能量型储能的使用寿命,提升了混合储能系统经济性。
4.2.3寿命损耗对混合储能系统配置结果的影响
为了分析并证明计及寿命损耗对合理配置储能的重要性,设置2种情形:(1)不考虑能量型储能寿命损耗;(2)考虑能量型储能寿命损耗。2种情形的混合储能系统各储能单元充放电状态如图3、4所示。
从图3中可看出,考虑寿命损耗后,能量型储能的充放电次数更少、充放电功率更小。从图4可知,两种情形下的功率型储能主要区别是充放电功率大小不同。将图3与图4对比发现,不考虑寿命损耗时,能量型储能和功率型储能的充放电次数几乎相同,并且能量型储能的充放电功率高于功率型储能。
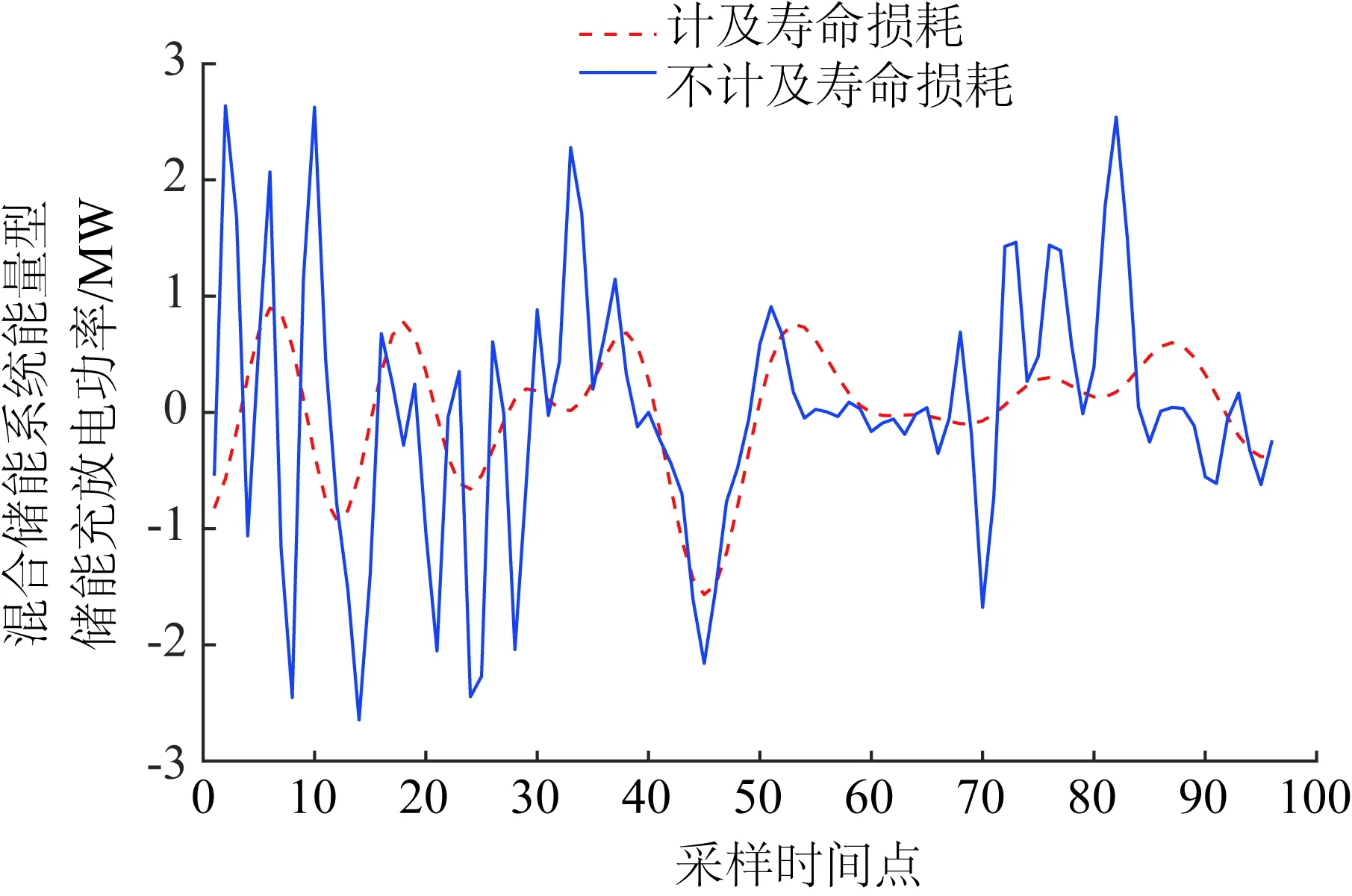
图3 能量型储能充放电功率Fig.3 Charge-discharge power of energy-type ESS

图4 功率型储能充放电功率Fig.4 Charge-discharge power of power-type ESS
这表明在不考虑寿命损耗时,能量型储能适合低频、低功率,功率型储能适合高频、高功率的特点没有得到体现。
考虑寿命损耗后,由于频繁、深度充放电会减少能量型储能的使用寿命,增加其投资运行成本,故能量型储能的充放电次数、充放电功率显著减少。
对应地,2种情形下的混合储能系统容量优化配置结果见表3。从表3中可知,在不计及寿命损耗时,能量型储能的容量显著增加,功率型储能容量减小,电能交易成本有略微减少,理论上的混合储能系统总成本也明显降低。之所以出现这种结果,是因为不计及寿命损耗时,能量型储能寿命损耗产生的运行成本未反映在总成本中。在这种配置下,功率型储能的作用十分有限,能量型储能在混合储能系统中承担了更频繁的充放电任务,充放电功率也更大。在实际运行时,混合储能系统运行成本会明显提高,增加系统实际投资成本。基于此条件下的配置结果会严重影响混合储能系统的经济性和技术性。
4.2.4混合储能系统和能量型储能配置方案对比
2种方案优化配置结果见表4。
表3寿命损耗对优化结果的影响
Table3Impactsoflifelossonoptimizationresults

表4 混合储能系统容量配置结果Table 4 Optimization results of HESS

在2种配置类型中,能量型储能的容量和功率几乎相同,电能交易成本也仅有微小差距,但混合储能系统可显著降低投资成本,提升经济效益。原因在于,本文所提出的储能系统优化配置模型,同时考虑投资成本和运行成本。在单一储能系统中,电网对于储能系统的功率需求仅由能量型储能满足。高频功率要求能量型储能频繁充放电,根据前文讨论,这会消耗能量型储能的使用寿命。储能使用寿命的减少意味着系统整体运行成本的增加。相对于单一储能,混合储能配置能充分利用功率型储能可频繁充放电的特点,将高频功率分配给功率型储能,使得能量型储能只承担低频功率,显著减少能量型储能的充放电次数,延长其使用寿命。虽然配置功率型储能会增加投资成本,但同时降低了系统运行成本。因此,虽然混合储能系统的投资成本比单一储能配置高,但其运行成本显著降低,整体经济性优于能量型储能。
5 结 论
本文综合考虑寿命损耗和优化运行对储能容量配置的影响,提出一种基于离散傅里叶变换的主动配电网混合储能容量优化配置模型。该模型基于离散傅里叶变换将混合储能系统功率分解成低频分量和高频分量,实现混合储能系统功率优化分配。计算能量型储能的充放电深度,分析能量型储能使用寿命受充放电循环等因素的影响。同时,利用配电网与上级电网的协调互动优化混合储能系统的充放电状态。通过算例分析,得出以下结论:
(1)混合储能系统的容量优化配置结果受频率分断点影响,总成本呈现先降后增的趋势;
(2)采用分时电价可大幅度降低混合储能系统投资运行成本,提升系统经济性;
(3)能量型储能寿命损耗会显著影响混合储能系统容量配置结果,在进行优化配置时,须计及能量型储能寿命损耗对优化配置结果的影响;
(4)混合储能系统可优化能量型储能充放电状态,延长能量型储能使用寿命,降低系统总成本。
目前,铅酸电池、液流电池、超级电容等储能设备的经济性、技术性和安全性仍待提高,尚不具备大规模推广应用的条件。但本文所建立模型适用不同类型的储能设备,具有一般性,不受目前储能技术限制,可为示范区或局部配电网中混合储能优化配置提供理论参考。
附录A
1 电价波动曲线
本文考虑市场环境下的分时电价和和电价交易差异,计算配电网与上级电网的电能交易成本。售电和购电电价见附表A1。
表A1售电及购电电价
TableA1Priceofpurchaseandsellenergy
电价波动曲线如附图A1所示。

图A1电价波动曲线
Fig.A1Electricitypricefluctuationcurve
2 系统参数
本文以改进的IEEE 14节点配电网为例进行分析。系统中的详细参数见附表A2—A4。
表A2风电机组参数
TableA2Windturbinegenerationparameters

表A3光伏机组参数
TableA3Photovoltaicparameters

表A4混合储能系统参数
TableA4Hybridenergystoragesystemparameters
3 算法流程
算法流程如附图A2所示。
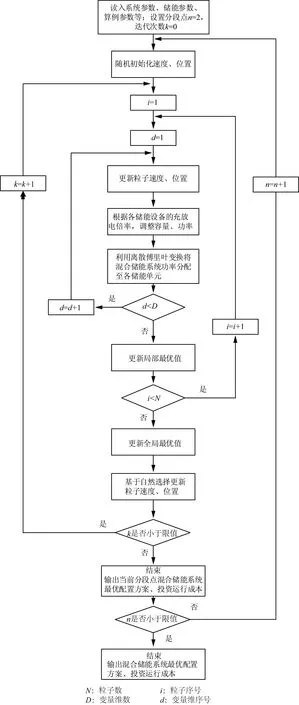
图A2算法流程图
Fig.A2Procedureoftheselectionbasedparticleswarmoptimizer
步骤1输入系统参数,包括系统参数、储能参数、算例参数等,迭代次数k=0,分段点n=2;
步骤2生成混合储能系统配置方案,混合型储能额定功率Pi和额定容量Ei;
步骤3生成混合储能系统运行方案,混合型储能系统充放电功率;
步骤4根据式(2)—(8)计算功率型储能和能量型储能充放电功率PEi(t);
步骤5计算能量型储能使用寿命Li,基于混合储能系统配置和运行方案,根据式(18)—(20)计算其实际使用寿命;
步骤6计算单个个体的适应度,根据式(9)—(10)计算混合储能系统投资运行成本;
步骤7更新全局最优值;
步骤8基于自然选择更新粒子位置和速度,k=k+1,若迭代次数k大于限值,则结束,输出当前分段点对应的最优混合储能系统优化配置方案,否则,转至步骤 2;
步骤9判断分段点是否枚举完毕,若是,则比较所有分段点对应的混合储能系统投资运行成本,取成本最小值对应的配置方案为最优配置方案,否则,k=0,n=n+1,转至步骤 2。
