基于临界车速的平面交叉口通行模式设计*

胡永举， 刘锦俐， 邱 欣， 陶珏强

(浙江师范大学 道路与交通工程研究中心,浙江 金华 321004)

0 引 言

平面交叉口是城市道路网络的节点，对整个区域交通的畅通起着至关重要的作用.解决城市交通拥堵的核心是提升交叉口的通行能力，使交叉口与路段的通行能力相匹配[1].传统的提升交叉口通行能力的方法主要包括道路拓宽改造及交通组织方式优化.由于道路拓宽改造的造价昂贵、改造后容易引起增量交通等问题，不利于道路交通的可持续发展，因此,选择更高效的交叉口交通组织方式显得尤为重要[2].特别是在小汽车保有量空前增长、路用面积日益匮乏的状况下，寻找新的、更加有效的交通组织方式是我国公路管理建设工作实现资源节约、环境友好的重要保证.

近年来，已有许多学者致力于交叉口交通组织方式的研究，研究成果颇丰，其中较为传统的组织方式主要包括设置左转待行区、综合待行区等.传统的交通口通行模式通过调整交通组织方式和交通控制方式，提升了交叉口的通行效率，其中，综合待行区是一个特殊的待行区，它的功能可在左转待行区、直行待行区及掉头待行区之间不断转换[3]，但会引发停车次数增多、待行区内空间利用不充分等问题；左转待行区采用将停车线的位置提前至冲突点前的方法提升交叉口内部空间的利用率，从而增加交叉口的通行能力，但会引发转弯半径不足，同时也会导致停车次数增多等问题[4].以上通行模式中，绿灯启亮后车辆从静止起动到加速通过交叉口内冲突点，车流运行轨迹不顺畅，车辆在交叉口内行驶时间较长，并且缓慢的车速将进一步导致车流集结波的形成[5].因此，在保证行车安全的前提下，合理设置停车线的位置，以提升车辆在交叉口的通行速度，对交叉口通行效率的提升具有重要意义.目前国内外对于该理论的研究还处于起步阶段，相关成果还较少.Van等[6]分析了进口速度较慢的车辆对环形交叉口通行能力的影响，在此基础上得出了环形交叉口通行能力的计算方法.白玉等[7]针对现有停车线设置过于提前的问题，提出了基于通行条件限制的停车线设计的实现目标及约束条件，构建了平面十字交叉口停车线设计的模型.刘丹[5]建立了环形停车线前置距离模型，并基于同出口车流提前放行的概念，提出了环形交叉口左直协同放行相位.曹森[8]基于饱和流率的思想，以安全行车为约束条件，以通行能力最大为目标，建立了基于停车线前置的信号交叉口通行能力计算模型，使交叉口内通行模式转变为路段通行模式.

临界车速vc为车流运行接近饱和流率时的速度[9].本文提出一种基于vc的平面交叉口优化控制方法，见图1.在保证行车安全的前提下，以通行能力最大和平均延误最小为目标，优化停车线位置及信号周期的设置，使本相位车流提前放行，并将冲突车流在时间上分离，放行车辆的车速在本相位车流与前一相位车流的冲突点前达到vc，并保持以vc的车速通过冲突点.结合VISSIM仿真对比了该优化通行模式与传统通行模式的优劣，以验证该方法的有效性和合理性.研究成果为寻找新的、更加有效的交通组织方式提供理论基础.

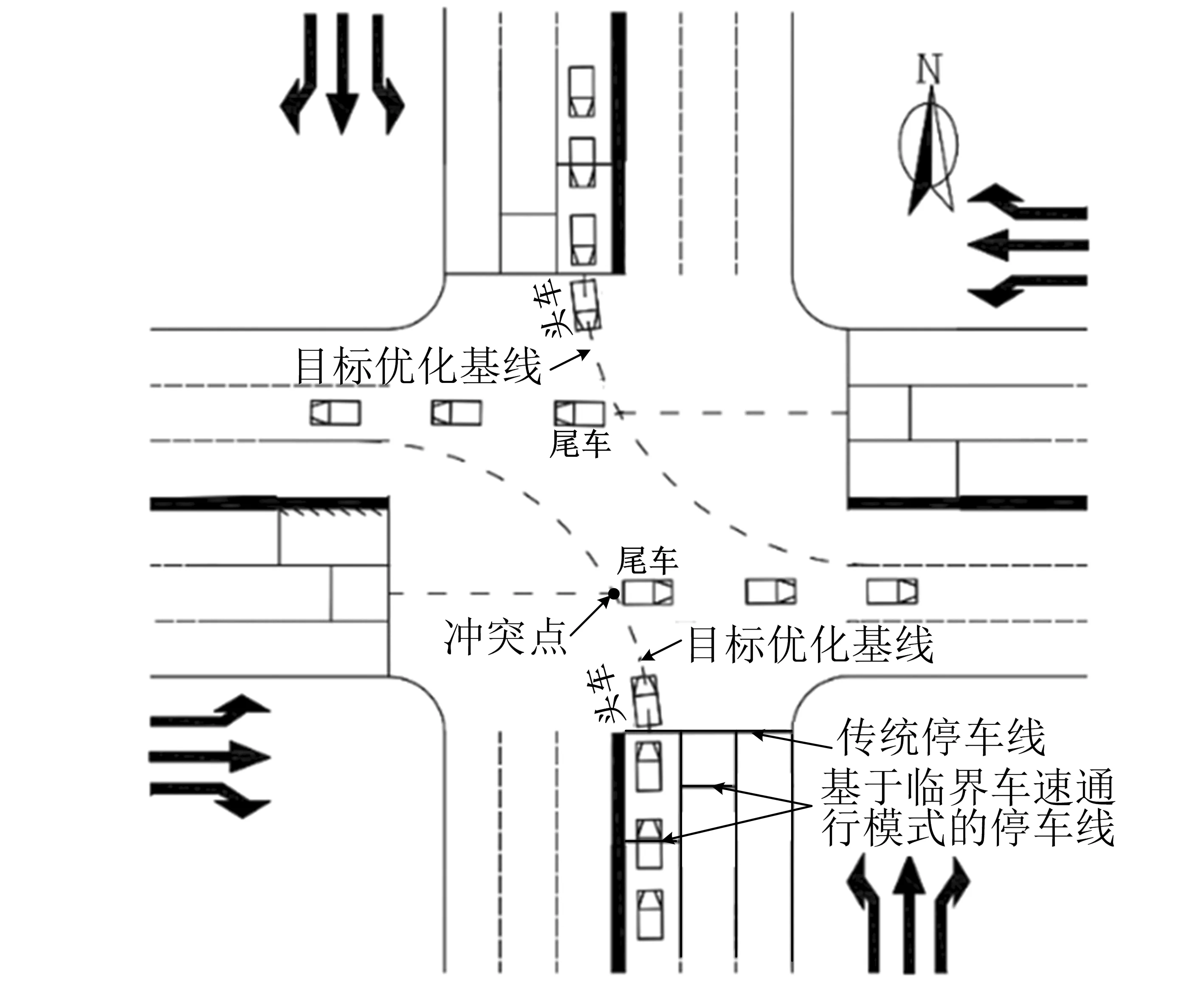
图1 基于临界车速的平面交叉口通行模式示意图

1 优化控制方法

为了便于研究基于vc的平面交叉口通行模式，主要考虑左转和直行机动车对交叉口通行能力的影响，不考虑右转对交叉口通行能力的影响.以中心对称的双向三车道的平面交叉口为例，其设置形式如图1所示，设计参数如图2所示(dm,ds,da的定义见下文).主要的控制思路如下，其他形式交叉口的优化步骤相同：

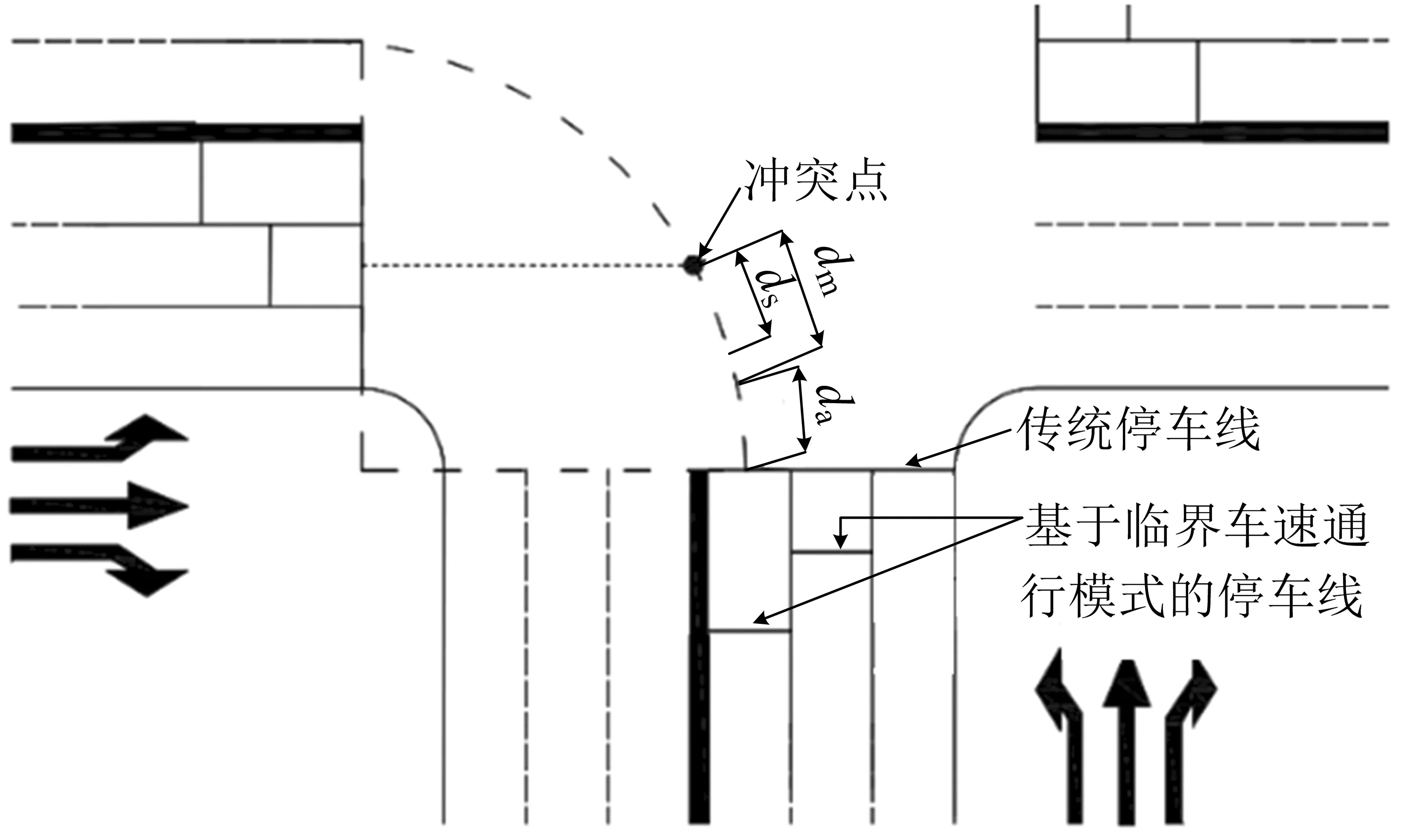
图2 设计参数示意图

1)计算vc.即计算车流运行接近饱和流率时的速度，是车辆在交叉口内的目标车速.饱和流率定义为：在一次连续的绿灯信号时间内，进口道上一列连续车队以最小安全车头时距通过基准断面的最大而稳定的流量[9].根据安全车头时距与速度的对应关系可知，安全车头时距随速度增大呈现先减小后增大的趋势，据此可计算出安全车头时距的极小值，即最小安全车头时距，由此可得vc.以最大通行能力和行车安全为原则，当车辆达到该速度后应保持匀速运行.

2)确定相位相序.信号相位相序的设置决定了相位间冲突点在交叉口内的分布位置，基于临界车速的平面交叉口通行模式宜采用四相位控制模式，分别设置左转、直行专用相位，在时间上分离左转车流和直行车流，并且左转相位与直行相位在一个信号周期内交替轮换，尽量使得冲突点延伸至交叉口中心部位.

3)确定相位间冲突点的位置.在信号相位已知的情况下，根据前后两相位车流运行轨迹，即可确定两两相位间冲突点的坐标，为下一步确定目标优化基线位置及安全距离奠定基础.

4)确定目标优化基线位置.在vc与目标优化基线位置已知的情况下，根据加速度计算公式可得停车线位置.目标优化基线为某一信号相位放行首车沿着车辆运行轨迹在交叉口内达到速度vc时的位置基线，该基线应位于冲突点前以保证车辆以vc的速度通过冲突点，此外冲突点到目标优化基线的距离dm应小于冲突点到传统停车线的距离，避免停车线后移过多，导致进口车道排队空间过小.

5)确定安全距离ds.即使得冲突车流在空间上分离的最小距离，以计算绿灯间隔时间.绿灯间隔时间为前一相位车辆尾车由静止开始起动行驶至冲突点的时间减去后一相位首车从停车线由静止开始起动行驶至冲突点前ds的时间.ds需满足本相位首车在前一相位尾车未清空的情况下，在冲突点前减速停车所需的距离.

6)计算绿灯显示时间.绿灯间隔时间是车流分离的保证，在此基础上基于Webster最佳信号周期配时公式计算各相位初始绿灯时间，并结合各相位车辆从停车线开始起动并到达目标优化基线的时间作为各相位绿灯的显示时间，即可得到交叉口信号配时.

2 优化控制方案

2.1 vc及dm的取值

vc为车流运行接近饱和流率时的速度，也是道路达到理论通行能力时的车速.理想状态下，某一排队车列以最小安全车头时距连续通过某一断面时，该断面通行能力达到最大.根据安全车头时距和速度之间的对应关系，找出达到安全车头时距极小值的车速范围，该速度区间的下限值即为vc.安全车头时距t*与速度v之间的对应关系为

式(1)中：t1为驾驶员反应时间，通常取2 s；φ为纵向附着系数，与车速v有关，车速与附着系数的大小成反比关系，可根据实际调查得到；d1为制动后车辆的安全间距;d2为平均车辆长度.

在vc及dm已知的条件下，即可反推停车线的具体位置.记由前后相位间冲突点沿着后相位车流运行轨迹到传统停车线的距离为d3，则dm∈(0，d3).若dm≤0，则无意义；若dm≥d3，则进口道排队空间过小，信号周期过长，通行效率降低.dm应以车辆平均加速距离及停车线后所需的车辆储存长度为设置依据.交叉口通行能力的计算以冲突点为界，当车辆通过冲突点后，才是严格意义上的通过交叉口[10].因此,在保证运行安全的前提下，选取d3作为目标优化基线位置存在一定的合理性.

2.2 停车线位置设计过程

2.2.1 相位相序设计

目标优化基线位置受冲突点位置的限制.信号相位相序是决定交叉口内车流冲突点位置的依据，因此,需优先考虑相位控制模式.基于临界车速的平面交叉口通行模式宜采用四相位控制模式，设置直行和左转专用相位，并且左转相位与直行相位在一个信号周期内交替轮换，尽量使得冲突点延伸至交叉口中心部位.由此，本文确定信号相位为四相位，信号相位控制模式如图3所示.根据交叉口的几何形式，即可得到冲突点在交叉口内的位置分布.

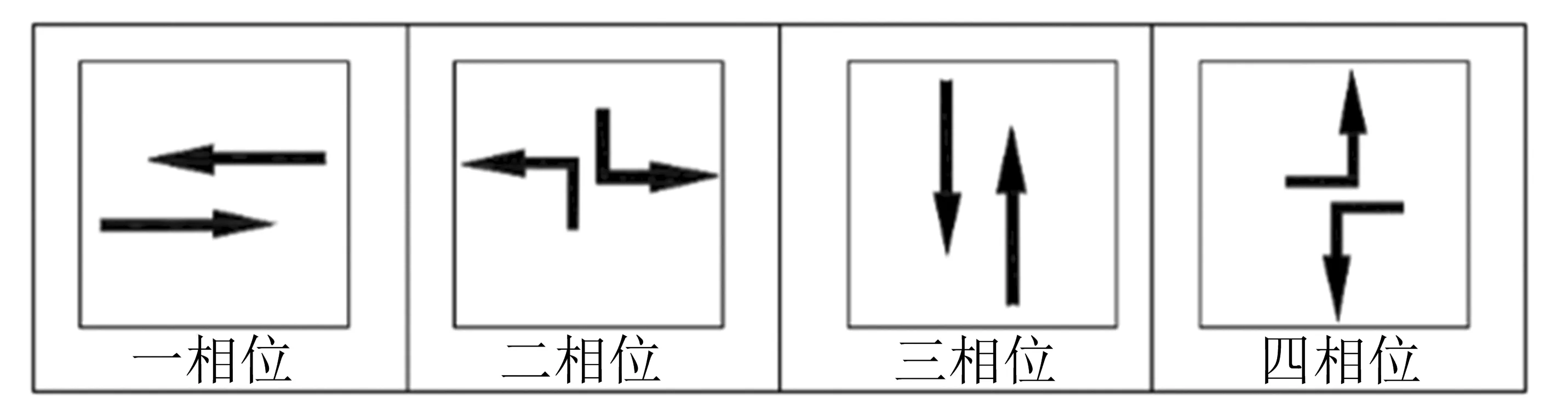
图3 信号相位控制模式示意图

2.2.2 车辆达到vm时的加速距离

车辆从静止开始加速直到vc，加速度逐渐增大，本文假设加速度a和时间t成正比，即

a=δt.

(2)

将式(2)两端积分,并令t=t0(t0为车辆从静止开始加速到vc所需的时间),得到车辆的末速度，即临界速度vc为

两端再次积分即得加速距离d为

式(2)～(4)中：d为沿着车辆运行轨迹由目标基线到停车线的距离；δ为加速度系数.

2.2.3 停车线位置优化方程

在vc,dm,d已知的情况下，即可求得某一进口某一转向车道停车线的位置.本文以dm与ds重合的条件为例，优化停车线位置.由于交叉口呈中心对称，所以各进口的左转停车线、直行停车线位置的优化方程各自相同.具体的优化步骤如下：

1)左转停车线位置优化过程

左转停车线位置优化设计参数如图4所示，左转车辆在交叉口内运行轨迹为圆弧，传统停车线到目标基线的弧长da可表示为

da=θ1×r-ds.

(5)

式(5)中：θ1为传统停车线到冲突点的弧度；r为左转轨迹半径.

左转车道停车线后退的距离ll为

l1=d-da=d-θ1×r+ds.

(6)

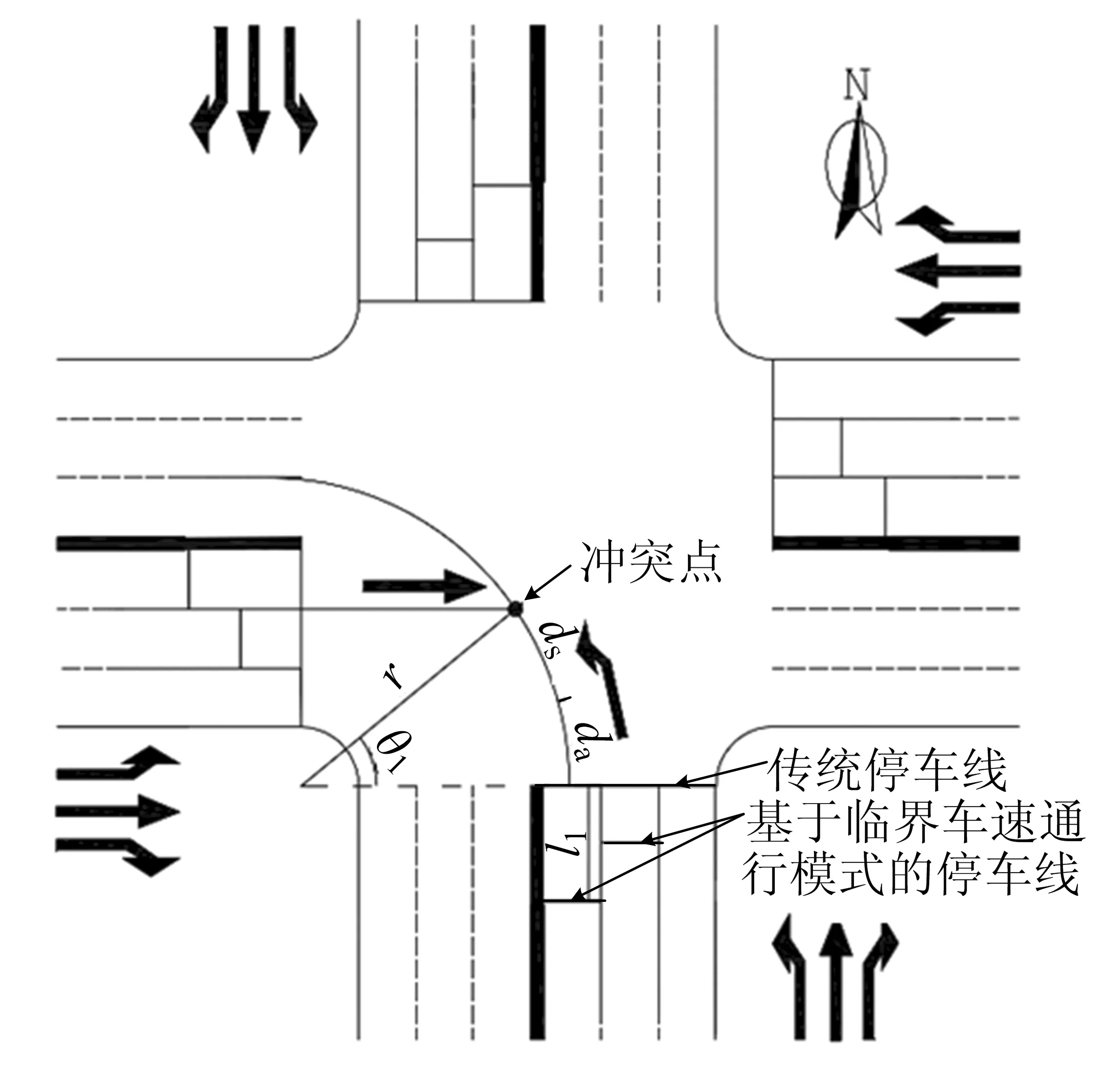
图4 左转停车线位置优化设计参数示意图

2)直行停车线优化过程

直行停车线位置优化设计参数如图5所示，交叉口直行车辆的运行轨迹为直线，传统停车线到目标优化基线的距离dt为

dt=l-r×sinθ2-ds.

(7)

式(7)中：l为交叉口宽度；θ2为左转弯车辆由传统停车线到冲突点的弧度；r为左转轨迹半径.

直行车道停车线后退的距离公式为

l2=d-dt=d-l+r×sinθ2+ds.

(8)

图5 直行停车线位置优化设计参数示意图

2.3 绿灯时间和绿灯间隔时间的确定

在相位相序已知的情况下，信号周期即由绿灯间隔时间及显示绿灯时间确定.

2.3.1 绿灯间隔时间

绿灯间隔时间是为分离本相位车队首车与前一相位车队尾车所需的时间，以保证行车安全[11]，即当本相位首车抵达冲突点时，前一相位尾车离开冲突点，重叠两相位车流部分放行时间.根据图3的相位相序设置，绿灯间隔时间主要分为前相位是直行时的绿灯间隔时间及前相位是左转时的绿灯间隔时间.

1)前相位是直行的绿灯间隔时间

直行车辆从停车线到冲突点的距离st为

st=r×cosθ1+d-l+r×sinθ2+ds.

(9)

则可得绿灯间隔时间tt为

2)前相位是左转的绿灯间隔时间

左转车辆从停车线到冲突点的距离sL为

sL=r×θ2+d-θ1×r+ds.

(11)

则可得绿灯间隔时间tL为

2.3.2 初始有效绿灯时间

交叉口各相位的初始绿灯时间应在交叉口初始周期确定的前提下，按照各方向车流的流量比来分配.

由上述计算过程可得绿灯间隔时间.平面交叉口的初始信号周期，可采用使车辆延误最小的Webster最佳信号周期C0进行计算.在此计算过程中，以目标优化基线作为最佳信号周期的计算参考线，不考虑前后损失时间，即

式(13)中：L为一个周期内总的损失时间(s)，包含周期内全红时间(即绿灯间隔时间)和起动、停车的损失时间；Y为一个周期内全部信号相位的最大y值之和，Y=∑y；y是流量与饱和流量的比值.

根据各相位车流流量比确定有效绿灯时间为

ge=C0λi,i=1,2,3,4.

(14)

式(14)中：ge为对应相位的有效绿灯时间；λi为对应相位的绿信比.

2.3.3 最终有效绿灯时间

绿灯显示时间即各相位允许车辆通行的时间.初始绿灯时间的计算是以各相位目标优化基线作为计算参考线，因此不能作为绿灯显示时间，应在各相位有效绿灯时间的基础上加上本相位车辆从停车线开始起动并到达目标优化基线的时间t2，作为最终有效绿灯时间，即

g=C0λi+t2i=1,2,3,4.

(15)

3 评价方案

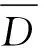
4 仿真分析

本文选取金华市海棠东路—东阳街平面十字交叉口为实例验证对象，对其交通现状展开调查.该交叉口为三进三出中心对称平面十字形交叉口，其交叉口车道功能划分及几何形态布局与图1相符，信号控制方式采用典型的四相位控制模式，左转、直行设专用相位，统计得到某周一早高峰期的实际车流数据如表1所示.本文结合海棠东路—东阳街平面十字交叉口的几何形状，利用VISSIM仿真软件对该交叉口展开仿真分析，结果表明仿真模型稳定可靠，能准确反映实际交通状况.基于此，对该交叉口进行优化通行模式设计并展开仿真分析.首先，搭建直径为33 m的三进三出中心对称平面十字形交叉口，各个进口道均为1条专用左转、1条直行和1条专用右转车道，在设计与评价过程中均不考虑右转车辆对交叉口的影响；其次，根据上述步骤进行相位相序及停车线位置的优化调整；最后，按照各个进口流量及转向状况，对该平面交叉口进行信号优化控制，得到信号配时方案(见图6)，其中信号周期为121 s，绿灯末尾采用2 s闪烁的方式提示绿灯即将结束，不设置黄灯时间.

在平面十字型交叉口的各进口流量、各方向转向比例及车辆组成不变的情况下，分别按照优化通行模式和传统通行模式进行仿真.其中相较于传统通行模式，优化通行模式直行车道停车线后退5.5 m，左转车道停车线后退2 m.考虑到大部分平面交叉口均采取右转车道渠化设计，所以在仿真过程中不考虑右转车流.其中仿真结果数据获取时段为200～1 760 s，数据采集间隔为120 s，共计得到13组数据(在120 s内测得的各数值的平均值).得到的对比示意图如图7所示，数据统计如表2所示.

表1 某周一早高峰期各进口流量统计表

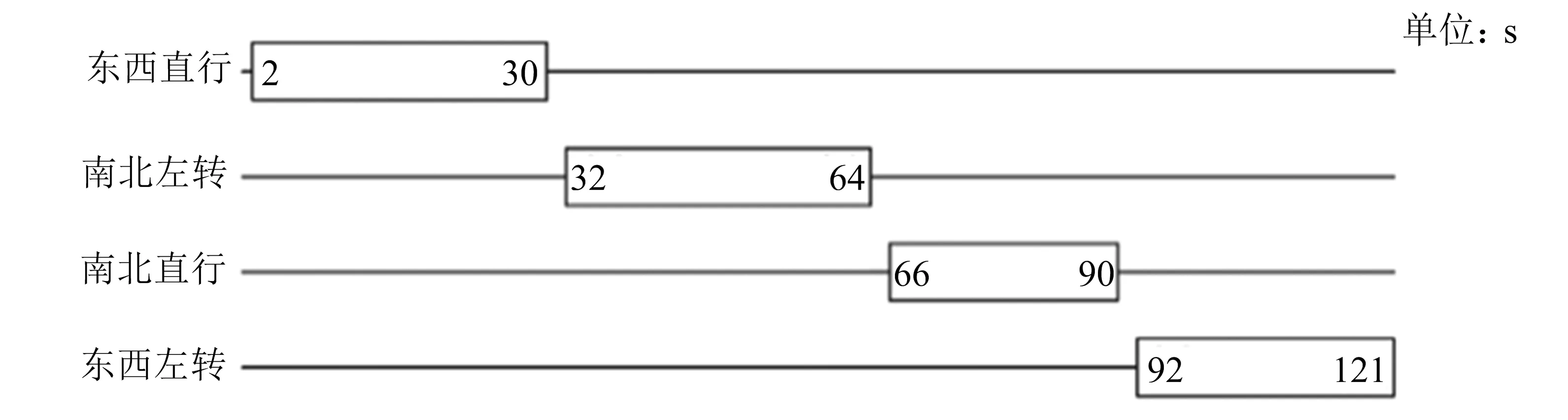
图6 优化信号控制配时方案图

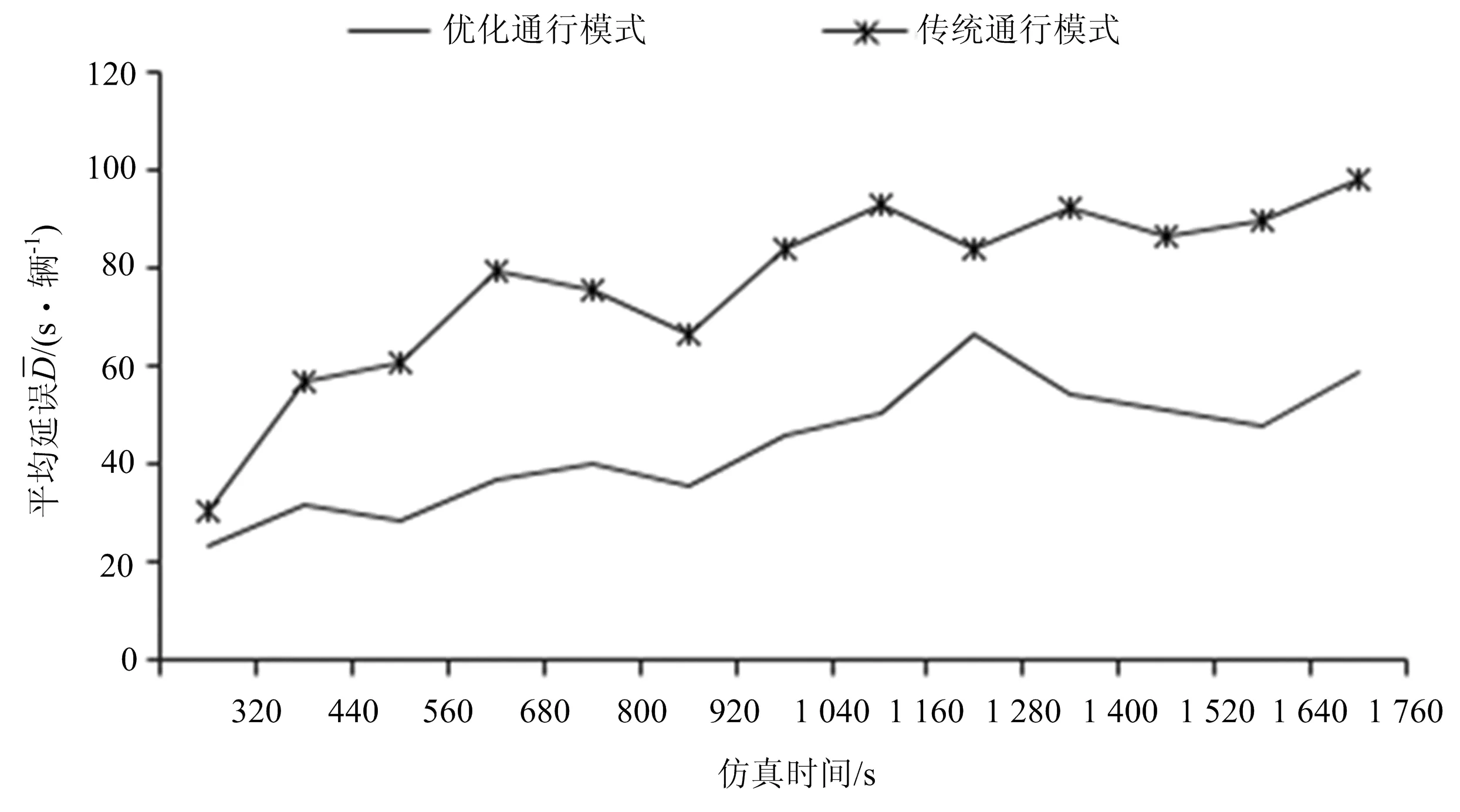
(a)交叉口车辆平均延误

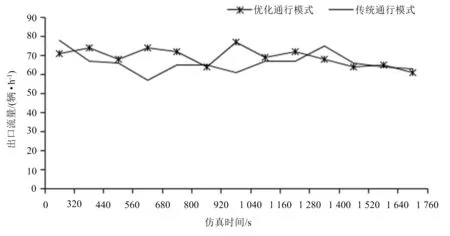
(b)出口流量

控制方案平均延误/(s5辆-1)出口流量/(辆5h-1)优化通行模式46.782 074传统通行模式68.711 984

由表2可知，在传统通行模式下，平面交叉口的车辆平均延误为68.71 s，出口流量为1 984辆/h.实施本优化通行模式以后，平均延误降低了31.92%，出口流量提升了4.54%.对比结果表明：与传统通行模式相比，优化通行模式在降低延误、提升交叉口通行能力方面均有有效提升.这说明本文所提的控制方案更加有效.

5 结 论

本文通过分析现有交叉口通行模式中存在的车辆运行缓慢、时空资源利用率低等问题，提出了基于临界车速最大化通行能力的思想，建立停车线位置后移及绿灯提前启亮的信号周期配时模型，提升了车辆的入口车速，缩短了信号周期时长，降低了车辆运行延误，提高了交叉口的通行能力，是对传统平面交叉口通行模式的补充和发展，具有一定的应用价值.此外，建立了评价分析方案，利用VISSIM仿真对该通行模式进行了验证.仿真结果表明：该交叉口通行模式在避免车辆排队溢出的条件下，车辆平均延误降低了31.92%，出口流量提升了4.54%.

对交通负荷较大、车辆转弯半径不足的交叉口，本优化通行模式的通行效率达到最佳.值得注意的是：1)考虑到交通安全，非机动车和行人宜采用地下通道完成过街行为；2)该通行模式下各相位绿灯时间将大幅度缩短，若无地下通道等过街设施，且相位绿灯时间过短，不能满足行人过街所需时间，则可考虑增加行人专用相位；3)为保证通行效率且防止车速过高，推荐以达到安全车头时距极小值的速度区间的下限值作为临界速度，并以此作为限制速度；4)若左转车道及直行车道停车线的后退距离足够，可考虑设置可变车道，即某一相位车辆放行时，车辆在到达停车线后，可借用相邻车道进入交叉口，增加进口道的数量.该方法可增加相位进口道数量，进一步提升交叉口资源的利用率，具体方法还需后续研究.