同宿轨向量场的特征扰动空间*
2018-08-08陈凤娟
钟 溢, 陈凤娟
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
0 引 言
同宿轨在动力系统的研究中有着悠久的历史,可以追溯到Poincaré在研究三体问题时发现的同宿缠结现象[1-3].该现象由稳定流形与不稳定流形横截相交,从而产生马蹄意义和似Hénon吸引子意义下的混沌[4-5].令d为稳定流形与不稳定流形之间的距离,经典的Melnikov函数[6-7]作为d的主项,在一定程度上反映了d的特性.文献[8]推导了高阶Melnikov函数,对距离d有了更精细的刻画,其中一阶Melnikov函数吻合于经典的Melnikov函数.本文通过高阶Melnikov函数分析距离d,研究了同宿轨向量场的一个新的扰动现象.首先给出如下定义:
定义1设X为光滑流形,F为X上的向量场,且F存在同宿轨.如果存在函数G,使得向量场F+εG(ε充分小)也存在同宿轨,那么称G为F的特征扰动函数.
定义2称所有特征扰动函数组成的集合为F的特征扰动空间,记为E(F),即
E(F)={G:G为F的特征扰动函数}.
下面考虑如下二维自治微分方程:
式(1)中:f(x,y),g(x,y),P(x,y),Q(x,y)为有界闭球V⊂R2上关于(x,y)的解析函数,且P(x,y),Q(x,y)不显含时间t.假设当ε=0时,方程(1)存在鞍点O(x0,y0)和同宿到O的同宿轨道(t)={(a(t),b(t)):t∈R}.

式(2)中,
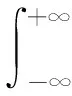
为Melnikov积分.下面将M和d(ε)视为扰动函数(P(x,y),Q(x,y))的泛函,记为M(P,Q)和d(P,Q),即
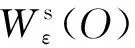
由文献[8]知,式(2)可进一步表示为
d(P,Q)=M0(P,Q)ε+M1(P,Q)ε2+M2(P,Q)ε3+…+Mk(P,Q)εk+1+….
(4)
式(4)中:Mk(P,Q)为高阶Melnikov函数;k=0,1,2,….由式(4)知,若对任意的非负整数k,Mk(P,Q)=0,则d(P,Q)=0.从而(f,g)的特征扰动空间为
E(f,g)={(P,Q):Mk(P,Q)=0,k=0,1,2,…}.
1 主要结论
下面给出本文的主要结果.
定理1对于方程(1),设a(t)是t的奇函数,b(t)是t的偶函数,且f(x,y)是x的偶函数,g(x,y)是x的奇函数,则(f,g)的特征扰动空间为
E(f,g)={(P,Q):P(x,y)是x的偶函数,Q(x,y)是x的奇函数}.
在证明定理1之前,先给出E(f,g)的性质.定义(P,Q)的范数为
‖(P,Q)‖=max{‖P‖0,‖Q‖0}.

定理2(E(f,g),‖5‖)是Banach空间.
证明 分两步证明.
1)∀α,β∈R,∀(P1,Q1),(P2,Q2)∈E(f,g),因为αP1+βP2是x的偶函数,αQ1+βQ2是x的奇函数,所以α(P1,Q1)+β(P2,Q2)∈E(f,g).因此,E(f,g)是线性子空间.
2)证明完备性.设{(Pn,Qn)}⊂E(f,g)为Cauchy序列.由于E(f,g)⊂C(V)×C(V),且C(V)×C(V)按范数‖5‖是Banach空间,因此,存在(P,Q)∈C(V)×C(V),使得(Pn,Qn)依范数收敛于(P,Q),即‖(Pn,Qn)-(P,Q)‖=‖(Pn-P,Qn-Q)‖→ 0,n→∞.于是
‖Pn-P‖0→0, ‖Qn-Q‖0→0,n→∞.
对任意(x,y)∈V,
|(P(-x,y),Q(-x,y))-(P(x,y),-Q(x,y))|≤
|(P(-x,y),Q(-x,y))-(Pn(-x,y),Qn(-x,y))|+
|(Pn(-x,y),Qn(-x,y))-(P(x,y),-Q(x,y))|=
|(Pn(-x,y),Qn(-x,y))-(P(-x,y),Q(-x,y))|+
|(Pn(x,y),-Qn(x,y))-(P(x,y),-Q(x,y))|=
因此,
(P(-x,y),Q(-x,y))=(P(x,y),-Q(x,y)),
即P(x,y)关于x是偶函数,Q(x,y)关于x是奇函数.从而(P,Q)∈E(f,g).定理2证毕.
2 Mk(P,Q)的推导
根据式(4),要证明定理1,只需证对任意的k≥0,Mk(P,Q)=0.令D={(s,z)∈R2:s∈(-∞,+∞),|z|
(x,y)=
式(6)中:(s,z)∈D;A(s,z),U(s,z),B(s,z),V(s,z)为
把A(s,z),U(s,z),B(s,z),V(s,z)在(s,z)=(t,0)处作Taylor展开,得
引理11)当n是奇数时,An,m(t),Un,m(t)是t的偶函数;当n是偶数时,An,m(t),Un,m(t)是t的奇函数.
2)当n是奇数时,Bn,m(t),Vn,m(t)是t的奇函数;当n是偶数时,Bn,m(t),Vn,m(t)是t的偶函数.
证明 不失一般性,只证明An,m(t)的奇偶性,其他函数的奇偶性可类似证明.

根据定理1的假设,可得上式分子部分是s的奇函数,分母部分是s的偶函数.因此,A(s,z)是s的奇函数.即对于任意的(s,z)∈D,
A(-s,z)=-A(s,z).
等式两边关于s求导,根据链式法则得
A1,0(-s,z)=A1,0(s,z);A2,0(-s,z)=-A2,0(s,z).
因为变量z与s相互独立,所以A1,0(s,z)关于z求导不改变其对s变量的奇偶性.这就意味着对于所有的整数m≥0,
A1,m(-s,z)=A1,m(s,z);A2,m(-s,z)=-A2,m(s,z).
归纳得
令(s,z)=(t,0),得引理1中的结论.引理1证毕.
下面求解方程(8).将式(9)代入式(8)得
由常数变易法,解得方程(11)在稳定流形上的解为
类似地,解得方程(11)在不稳定流形上的解为
由式(12)和式(13)知,Z+(t),S+(t),Z-(t),S-(t)可写成如下级数形式:

其中,K为常数,视具体得到的系数项而定.
于是,稳定流形与不稳定流形之间的距离为Z+(t)及Z-(t)在t=0处的值之差,即
引理2对于t≥0,有
证明 运用数学归纳法.首先,当k=0时,
在式(7)中令(s,z)=(t,0)可知,U(t,0)是t的奇函数,B(t,0),V(t,0)是t的偶函数,E(t,τ)关于t,τ都是偶函数.由积分变量代换得
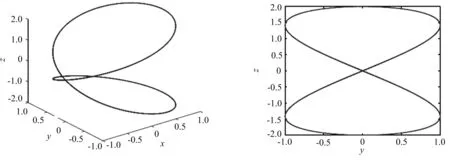
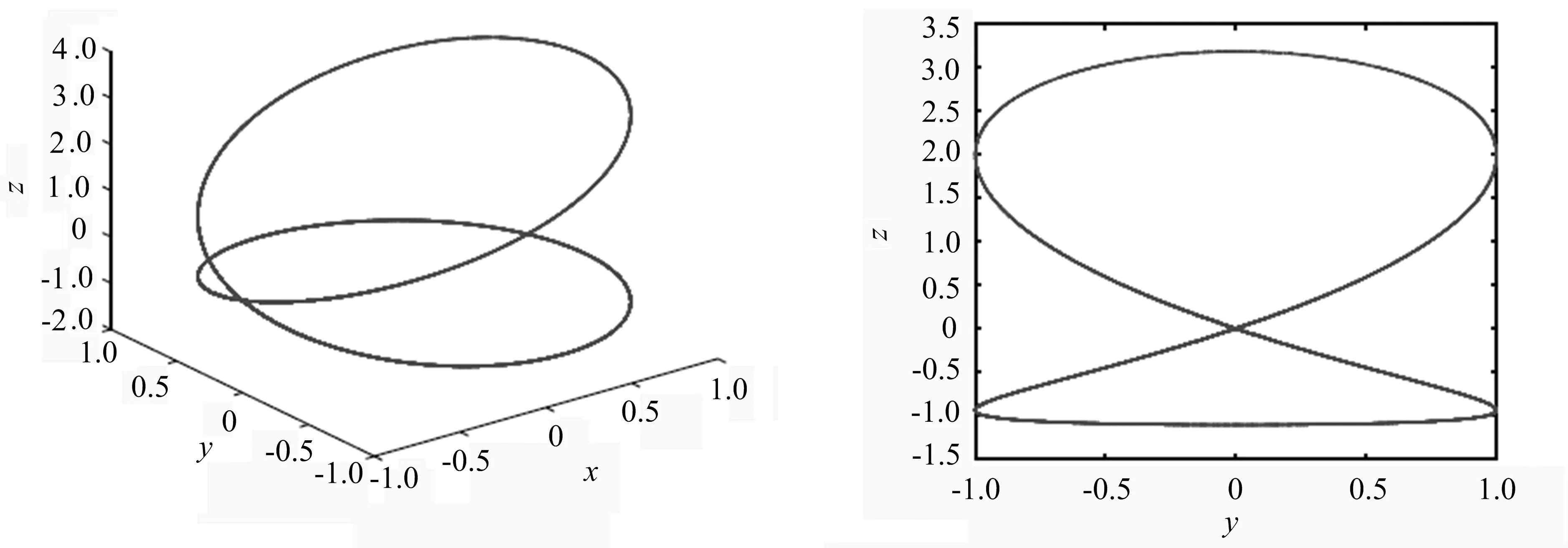
假设引理2的结论对正整数k 而ρ 于是 结合引理1得到 因此 引理2证毕. 由式(4)得d(P,Q)=0.于是方程(1)存在同宿轨.根据定义1 知,(P,Q)为向量场(f,g)的特征扰动函数.从而证得E(f,g)是向量场(f,g)的特征扰动空间.定理1证毕. 令S1=R/{2nπ},n∈Z.考虑如下系统: 式(20)中,(θ,v)∈S1×R.当ε=0 时,方程(20)有1个鞍点O(±π,0)和2条同宿到O的同宿轨道±,表达式为 ±=(±2arctan(sinht),±2secht),t∈(-∞,+∞). 比较式(1),此时a(t)=±2arctan(sinht)为t的奇函数,b(t)=±2secht为t的偶函数.f(θ,v)=v,P(θ,v)=0为θ的偶函数,g(θ,v)=-sinθ,Q(θ,v)=vsinθ为θ的奇函数.从而由定理1知,(0,vsinθ)为同宿轨向量场(v,-sinθ)的一个特征扰动函数.图1为方程(20)当ε=0时在柱面S1×R上的相图,图2为图1在yoz平面上的投影. 图1 方程(20)在ε=0时的同宿轨 图2 图1在yoz平面上的投影 当ε=0.8时,图3和图4分别给出了方程(20)的同宿轨及其在yoz平面上的投影. 图3 方程(20)在ε=0.8时的同宿轨 图4 图3在yoz平面上的投影 当ε=-0.8时,图5和图6分别给出了方程(20)的同宿轨及其在yoz平面上的投影. 图5 方程(20)在ε=-0.8时的同宿轨 图6 图5在yoz平面上的投影 同宿轨的不稳定性导致了复杂的同宿缠结和混沌现象.本文通过高阶Melnikov函数研究了一类向量场自治扰动下的同宿轨持续性问题,得到了它的特征扰动空间,并证明了它是Banach空间.特征扰动空间对结构不稳定向量场的理解具有积极意义,相关结果可推广至异宿轨向量场.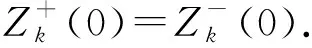
3 具体例子
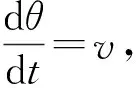

4 结 语
