基于二阶锥方法的仿人机器人稳定性控制*

朱毅康， 褚亚飞， 凌达峰， 朴松昊， 钟秋波

(1.浙江师范大学 杭州幼儿师范学院，浙江 杭州 311231；2.上饶职业技术学院 实训中心，江西 上饶 334109；3.哈尔滨工业大学 计算机科学与技术学院，黑龙江 哈尔滨 150001；4.宁波工程学院 电子与信息工程学院，浙江 宁波 315016)

0 引 言

仿人机器人可以如人一般在地面上行走，做许多动作，对其研究多采用近似化处理[1].稳定性控制是仿人机器人研究的热点[2-3]，其稳定性控制方式有多种选择，通常是录入参考量，并由这些参考量来对具体的运动进行动态修改.国内外相关学者对其进行了研究.Kagami等[4]给出了一种动态的平衡算法对机器人进行节点的跟踪改良，力保其误差缩小到可控制范围之内，并且对COM的投影ZMP进行有效的控制和预设；付根正等[5]考虑各关节对ZMP的影响，先模拟给出ZMP的误差，再利用二次规划方法和质心的Jacobian矩阵求解出每个关节的校正量，作进一步校正，提高步行稳定裕度；张继文等[6]根据步幅跟随规划算法提出了7个关键参数，并对其优化，建立了仿真模型，通过Latin超立方初始实验和EGO迭代建模优化求解，实现步行速度和稳定度的提高.

尽管上述研究都提出了相关的方案，提高了稳定性，但是由于环境的复杂性和多自由度的控制，对于仿人机器人运动稳定性控制仍需设定多种稳定性判断准则和约束条件，这就需要一种能够对多个性能因素和影响其控制的相关条件进行有效把握的方法.二阶锥方法正好可以解决这个问题.

二阶锥规划的具体操作是：先把目标函数转换成约束函数，并在合理的范围内进行更换，从而得到新的目标函数，并和原变量组合成新的变量，二阶锥约束条件则保持不变，然后把目标函数和约束函数用相关的符号形式表达出来，再运用二阶锥进行相关公式的计算便可以得出答案.二阶锥方法能够对几个参数同时进行优化[7]，且范数准则能够采用二阶锥得以实现[8].同时，二阶锥方法还能够处理时域和空域的各种鲁棒滤波器[9].因为二阶锥会涉及到凸集优化方面的问题，所以多半会使用罚函数解决相关问题.一般来说，30多次的更迭计算就能够得到比较理想的数值，并且其迭代的次数可以不被其他维数所干扰[7].

本文采用二阶锥控制方法，对运动过程中的稳定性进行联合约束，通过仿真实验，从多个方面进行对比验证，说明该方法能有效地控机制器人的运动稳定性.考虑仿人机器人的步态规划，选用7连杆模型[10]作为研究对象，不考虑双臂和头部，机器人身体由刚性连杆构成，用关节连接各连杆，脚部2个，小腿部2个，大腿部2个，身体部1个，共7个连杆.不考虑z-y横垂面的7连杆z-x简要模型如图1所示.

图1 7连杆仿人机器人简要模型

1 二阶锥规划原理

二阶锥规划的具体内涵其实就是围绕凸规划问题中的子集进行的，该原理需要满足二阶锥约束及线性等式约束的相关要求下，才能将线性函数最小化,具体的表达如下所示[7]：

(2)

Fy=g.

(3)

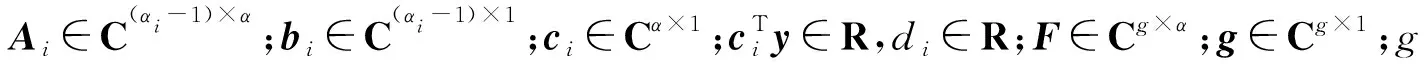
式(2)的每个约束条件可定义为

式(3)的约束可以定义为零锥，即

g-Fy∈{0}g，

而零锥{0}g定义为

{0}g{x|x∈Cg×1,x=0}.

从上面公式可以知道，当αi=1,i=1,2,…,N时，就变成了二阶锥规划的特例：线性规划和凸二次规划.

二阶锥优化的几何意义需要在二阶锥内部最优点位中体现出来，该点位能够实现所求对象数值的最小化.用式(2)表示整个圆锥体中除闭口之外的其余部分;同时，用式(3)表示圆锥体的闭口部分.由其所构成的圆锥体的点位对应式(1)中的每组状态变量.将式(1)表示所求对象的函数，从而来表达状态变量和目标变量之间的具体数值和关系.当状态变量和目标变量之间形成了无穷小的差值时，便能够得到一组最佳的状态变量.对符合式(2)和式(3)的控制变量进行不断迭代，并用式(1)与之产生的状态变量进行比较.一直等到迭代结束或者满足一定条件时便可停止运算，此刻的变量便处于最佳状态.

然而,机器人重心处于一个比较高的位置，因此,其双脚用于支撑的面积会比较小，这些仿人机器人在其运动过程中就不能保持稳定.因此,使用二阶锥规划方法能够对在摩擦力、ZMP及运动当中产生的动能这3个方面[11]对仿人机器人进行约束.这里简要罗列约束条件，具体不展开论述.

1)摩擦约束

‖PxyF0‖≤μF1；

(4)

‖PmzF0-pzmp×PxyF0‖≤μrF2；

(5)

F1+F2≤PzF0.

(6)

式(4)～(6)中：Pxy为x-y平面力；Pmz和Pz是与z坐标相切力在不同平面产生的投影矩阵；pzmp是假定范围内的ZMP；μ为摩擦系数；μr为移动产生的扭动摩擦系数；F0,F1和F2分别是阻止机器人前向运动、切向运动和正常运动时产生的摩擦力.

2)ZMP约束

Aspzmp+bs≤0；

(7)

3)动能约束

设q为仿人机器人转动关节的转动角度响应；Td(tk)为时间tk的优化期望响应；p为误差范数;P为1,2和∞时的动能约束,即

2 二阶锥问题的构建

以式(10)来看，需要把优化问题换算成二阶锥规划问题来进行解答.

加入一组非负变量εk(k=1,2,…,K)，式(10)就可用以下形式表示：

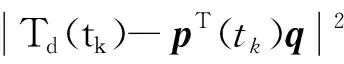
(12)

其中,约束条件为式(4)～式(8).

3 二阶锥问题的解法

对于式(12)中的二次不等式约束，有

从而

进一步得

‖2≤(εk+1)2,

即

(13)

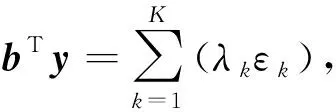
s.t

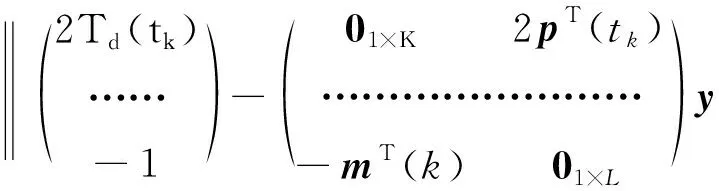
1+(mT(k)01×L)y.

(14)

可采用内点法对式(14)进行求解[7].

4 仿真实验

本文仿真试验使用MOSEK集团开发的基于Matlab的工具箱mosek8.0.假设机器人的力矩能够达到一种平衡的状态，那么可设其地面摩擦系数为0.5，扭动摩擦系数为0.6.将所有的数据运用到二阶锥规划方法中，并且将Matlab的相关技术与时间点进行跟踪控制，由此保证机器人在实验过程中能够维持一个平衡状态.

测试时间设定为0.8 s，这个测试时间能足够满足机器人瞬时行走的平稳性测试.将每步的时间设定为0.1 s，且假设仿人机器人的移动速度为0.3 m/s，质量为m,那么根据计算能得出其运动产生的动能为0.03 J.具体的结果如图2和图3所示.其中,图2是仿人机器人的动能仿真数据，图3是机器人在2种不同方案下的时延对比线性图.

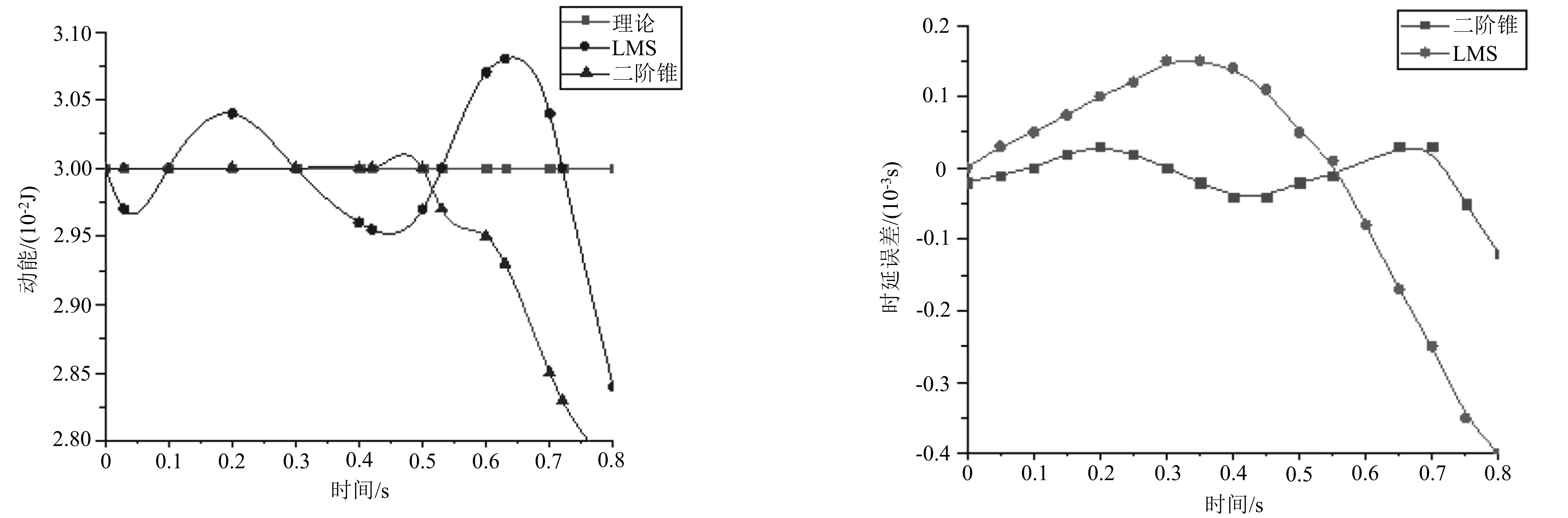
图2 动能 图3 时延

由图2可知,在0.5 s后二阶锥和LMS得出的曲线和理论轨迹曲线之间的偏差值都比较大.另外,将0.5 s作为一个分界线，可以观察到在这个分界线之前，二阶锥轨迹曲线跟理论上的描述较为一致；相反,LMS与理论曲线的分歧明显.因此，二阶锥方法比LMS方法具有明显的拟合优势.所以,小于0.5 s的计算周期就能保证机器人的运动维持在一个平稳的状态，使它的各个性能达到最佳的程度.二阶锥和LMS各有利弊，但二者都能够加快优化的速度，且将误差控制在较小的范围之内，为机器人提供一个更加稳定的运行环境.通过图3可以看出，测试的时间越长，需要迭代的次数就越多，这时二阶锥时间延迟误差小的优势就越发显现出来.

接下来，用二阶锥优化算法和基本微粒群优化算法对迭代误差效果及位移误差效果作对比，其中微粒的粒子一共有40个.另外，每一个维数均为7且其迭代因子c1=3,c2=3；惯性权重w=0.8；迭代次数约为500；机器人沿标识直线行走，测试行走偏移误差；测试距离为5 m.

图4 迭代误差 图5 位移误差

图4为2种优化算法在迭代误差效果方面的比较图，可以看出:二阶锥优化算法的迭代误差从一开始就比微粒群优化算法的收敛速度更快，并且在迭代160次左右才开始趋于稳定;而微粒群优化算法的震荡幅度比较大，在迭代280次左右才开始趋于稳定.

因为机器人运动平面会出现不平整等问题，并且机器人也没有视觉导航配置，所以在其运动过程中有可能会偏离预设的轨迹从而产生位移误差.图5为2种优化算法对位移误差的比较图，可以看出，二阶锥优化算法产生的误差比较小，与微粒群的优化算法相比,其误差更是微小.

图6和图7分别是采用二阶锥优化算法前后研究对象运动的ZMP轨迹图.不难发现，在使用优化算法之前的ZMP轨迹呈现出一种稀疏分散的状态，并不是所有的轨迹都在多边形内；而使用优化算法之后，ZMP轨迹基本落在支撑多边形以内.

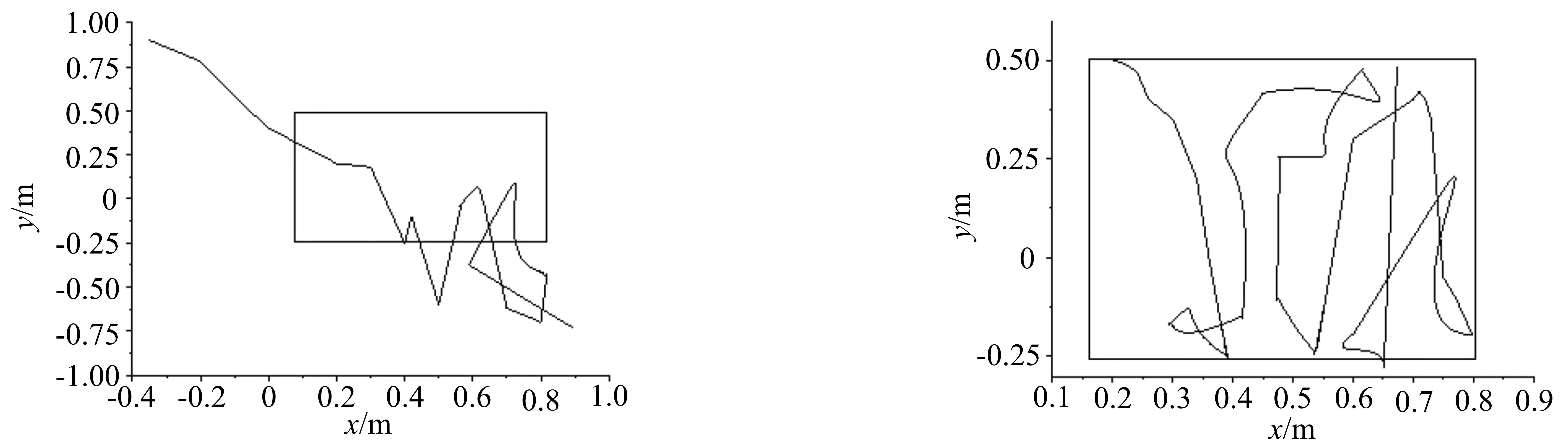
图6 优化前的ZMP轨迹图 图7 优化后的ZMP轨迹图

5 结 语

针对仿人机器人运动过程中的稳定性控制问题，提出了二阶锥方法，并将其转变为二阶锥控制方式，最后通过仿真实验，从动能、时延误差、迭代误差、位移误差、算法优化前后ZMP轨迹和LMS与微粒群算法作了详细的对比分析，结果显示：二阶锥方法在各方面都有明显优势，从而表明了该控制方法的有效性，能够提高机器人在运动过程中的稳定行性.