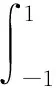ω条件下Ulm-like方法的收敛性*

2018-08-08沈卫平徐丽华周文静

浙江师范大学学报（自然科学版） 2018年3期

关键词：收敛性牛顿整数

沈卫平, 徐丽华, 周文静

(浙江师范大学数理与信息工程学院,浙江金华 321004)

0 引言

设X和Y是Banach空间,D是X空间中的开子集,f:D⊆X→Y是具有连续Fréchet导数f′的非线性算子.本文考虑非线性算子方程

f(x)=0

(1)

的求解问题.该问题是计算数学的理论基础,也是现代科学计算的核心问题之一.求解该问题最经典的方法是牛顿法.给定初始点x0∈D,牛顿法的迭代公式为

xk+1=xk-f′(xk)-1f(xk),k=0,1,2,….

(2)

由于重要的理论基础和广泛的应用背景,牛顿法的收敛性得到了广泛研究[1-5].

随着现代科学计算的发展,在应用领域中遇到的计算问题越来越复杂.另一方面,正如式(2)所示,牛顿迭代法的每一步迭代均要计算f′(xk)及求解Jacobian方程

f′(xk)(xk+1-xk)=-f(xk),

这就导致牛顿法的计算效率低,尤其当f′(xk) 阶数较大时.为了避免求解Jacobian方程,文献[6-8]提出了非精确牛顿法,即只求出Jacobian方程的近似解;文献[9-12]则使用了Ulm方法,给定初始值x0∈D,B0∈L (Y,X)(L(Y,X)表示Y到X的线性有界算子空间),Ulm 方法的迭代格式为

其中,k=0,1,2,….当Fréchet导数f′在方程的解附近满足Lipschitz条件时,文献[13]证明了Ulm方法在避免求解Jacobian方程的同时还能保持二阶收敛速度.

近年来,Ulm方法被用来求解逆特征值问题和逆奇异值问题[14-15],这两类问题最后都被归结为非线性方程的求解.但在实际求解中,因为Ulm方法在每次迭代中仍然需要求f′,所以当涉及的矩阵阶数较大时,计算会很费时.为了克服这个缺点,文献[16]提出了Ulm-like方法,即用满足一定条件的Ak+1近似代替f′(xk+1),从而可以避免求Jacobian矩阵,提高计算效率.给定x0∈D,B0∈L (Y,X),Ulm-like方法迭代公式为

式(3)中,k=0,1,2,….文献[16]主要证明了Fréchet导数f′在方程解附近满足Lipschitz条件时,Ulm-like方法具有二阶收敛速度;以文献[16]为基础,文献[17]将f′在解附近满足的条件推广到Hölder条件,且此时Ulm-like方法具有超线性收敛速度.

Lipschitz条件或Hölder条件是分析迭代法收敛性时常用的假设条件,但并不是所有方程都会满足二者之一的.下面的Hammerstein型非线性积分方程[18]即为一个例子:

其中:-∞

ω(θ)=∑mi=1Kiθpi,并要求ω是定义在[0,+∞)上连续非减的函数,且ω(0)≥0[19-21].此外,假设存在常数p∈(0,1],使得ω(tθ)≤tpω(θ)对任意的t∈[0,1]和任意的θ>0都成立.在这些条件下,文献[19]分析了牛顿法的半局部收敛性,并证明了其R-收敛阶至少为1+p.

本文研究Ulm-like方法的局部收敛性.在ω条件下,证明了由Ulm-like方法产生的序列是超线性收敛的,并且给出了收敛球的半径估计.注意到当ω(θ)=Lθ,L>0时,该条件便转化为Lipschitz条件,此时可得到文献[16]中的结论;当ω(θ)=Kθp,K>0,p∈(0,1]时,ω条件即为(K,p)-Hölder条件,此时可得到文献[17]中的结果.最后通过数值例子验证了本文得到的收敛性结果.

1 收敛性分析

设非线性算子f:D⊆X→Y有连续Fréchet导数f′,x*∈D是非线性方程(1)的解,B(x*,r)⊆D表示在X中以x*为中心、r>0为半径的开球.假设f′(x*)-1存在且f′在B(x*,r)内满足下列ω条件:

‖f′(x)-f′(y)‖≤ω(‖x-y‖), ∀x,y∈B(x*,r).

(4)

式(4)中,ω是定义在[0,+∞)上连续非减的函数,且ω(0)≥0.另外,假设存在常数q∈(1,2],使得函数ω满足以下条件:

ω(tθ)≤tq-1ω(θ), ∀t∈[0,1], ∀θ∈(0,+∞).

(5)

设{xk}是由Ulm-like方法(式(3))产生的序列,又设{Ak}⊂L (X,Y).对任意的k=0,1,2,…,Ak满足

‖Ak-f′(xk)‖≤γk‖f(xk)‖q-1.

(6)

(7)

则有如下引理(该引理对定理1的证明起到关键作用):

引理1假设f′及函数ω满足式(4)和式(5),又设k为任一自然数且Ak满足式(6).若xk∈B(x*,R),则

1)‖Ak-f′(xk)‖≤γηq-1‖xk-x*‖q-1;

结合式(4)、函数ω的非减性及η的定义,可推得

再由式(6)、式(9)及γ的定义可知,

‖Ak-f′(xk)‖≤γk‖f(xk)‖q-1≤γηq-1‖xk-x*‖q-1,

(10)

于是结论1)成立.

下证结论2)也成立.注意到‖xk-x*‖

‖Ak-f′(x*)‖≤‖Ak-f′(xk)‖+‖f′(xk)-f′(x*)‖≤

γηq-1‖xk-x*‖q-1+ω(‖xk-x*‖)≤

γηq-1‖xk-x*‖q-1+‖xk-x*‖q-1ω(1)≤[ω(1)+γηq-1]Rq-1.

进一步,由R的定义可得

‖f′(x*)-1‖‖Ak-f′(x*)‖≤‖f′(x*)-1‖[ω(1)+γηq-1]Rq-1<1.

从而,根据Banach引理可知Ak可逆,并且

再由ρ的定义得结论2)成立.引理1证毕.

下面给出主要结论.在ω条件(式(4))下,Ulm-like方法的收敛阶为q,即超线性收敛到解x*.为此,假设μ>0且设初始值B0满足

‖I-B0A0‖≤μ.

(11)

定理1设x*∈D是非线性方程(1)的一个解,且Jacobian矩阵f′(x*)可逆.假设f′及函数ω分别满足式(4)与式(5).若对任意非负整数k式(6)成立,则存在常数δ,μ>0,使得对任意的x0∈B(x*,δ)和任意满足式(11)的B0,由Ulm-like方法产生的序列{xk}超线性收敛到x*.此外,对任意非负整数k,下面2个估计式成立:

式(12)和式(13)中,τ>0是一个常数.

证明令

则0<τ<1显然成立.另外,设δ,μ满足

下面利用数学归纳法证明式(12)和式(13)对任意非负整数k均成立.首先,由x0∈B(x*,δ)知‖x0-x*‖<δ.再结合式(15)中δ满足的条件进一步可知当k=0时式(12)成立.另一方面,从式(11)和式(15)可推出

注意到0

由式(16),qm>1及式(14)可知

根据引理1(k=m),有

xm+1-x*=xm-x*-Bm(f(xm)-f(x*))=

由式(16)可得

由0<τ<1,1

故结合式(17)与式(19),有

其次,由式(17)、式(21)及式(18)可知