重视运算说理,优化运算思维,提高运算能力
2018-08-07商丹青
商丹青
【摘要】运算是数学的重要内容,运算的正确、灵活、合理和简洁是运算能力的主要特征。教学运算的基础知识应让学生清楚地意识到实施运算中的算理,学生只有理解了计算中的算理,才能够理解和掌握计算方法,才能正确、迅速地运算。小学数学计算教学的重点除了教给学生正确、基本的计算程序以外,教师更应该使学生掌握一系列的计算策略,逐步形成运算技能,并将运算提升到思维的层面。思维的“多层次”,在于学生从众多的解法中比较、反思、分析出解法的优劣,最终能够选择合理简洁的运算途径,这是运算能力发展的重要内容,也是运算思维达到一个新的高度的重要标志。
【关键词】运算能力;说清算理;算法优化
运算是数学的重要内容,在义务教育阶段的数学课程的各个学段中,运算都占有很大的比重。学生在学习数学的过程中,要花费较多的时间和精力去学习和掌握关于各种运算的知识和技能。《标准(2011年版)》指出:“运算能力主要是指能够根据法则和运算规律正确地进行运算的能力。”运算的正确、灵活、合理和简洁是运算能力的主要特征。
运算能力的形成不是一蹴而就的,运算能力的发展总是从简单到复杂、从低级到高级、从具体到抽象,有层次地发展起来的。因此,从低年级起,打好学生的运算基础就显得尤为重要。低年级孩子不具备一定的抽象思维能力,他们的计算往往是单纯的记忆或简单的模仿,缺乏学习兴趣和真正的理解,这样掌握的计算,往往会出现错误,是很多孩子运算能力差的一个重要原因。所以,在适度的训练,逐步熟悉的基础上,对运算的基础知识不仅应“知其然”,更应“知其所以然”,清楚地意识到实施运算中的算理。算理,从字面理解,既为运算的原理或道理,是解决问题的操作程序,解决“为什么这样算”的问题。学生只有理解了计算中的算理,才能够理解和掌握计算方法,才能正确、迅速地运算。
“口算两位数减一位数(退位减)”是苏教版一年级下册第79-80页内容。之前学生已经学过“口算两位数加一位数(进位加)”,这些是后面进一步学习稍复杂的笔算加减法的基础。教材提供了30-8 、34-8两道例题,教材上呈现的都是同一种算法,即从十位退一到个位,个位加十再减,十位退1再减。我反复研读教材,以及根据自己多次教学这部分内容的个人经验,我认为这两道例题尤其是34-8,可以挖掘出多种算法,对于激活学生的思维灵活性很有帮助,并且能教会学生根据不同的题目合理选择不同的算法,而让学生真正理解每种算法的算理,并能自主优化,就显得格外重要。例题的教学主要分两段进行:
【片段一】教学30-8
师:30 - 8,你会算吗?先想一想,如果有困难可以用小棒摆一摆。
学生自己试着算一算,摆一摆,教师巡视。
组织反馈:
指名演示摆法,边用小棒摆一摆,边说一说自己是怎样想的。(先摆3捆小棒,表示30,拿出1捆拆开变成10根,从10根中去掉8根,剩下的2根和2捆合起来就是22根)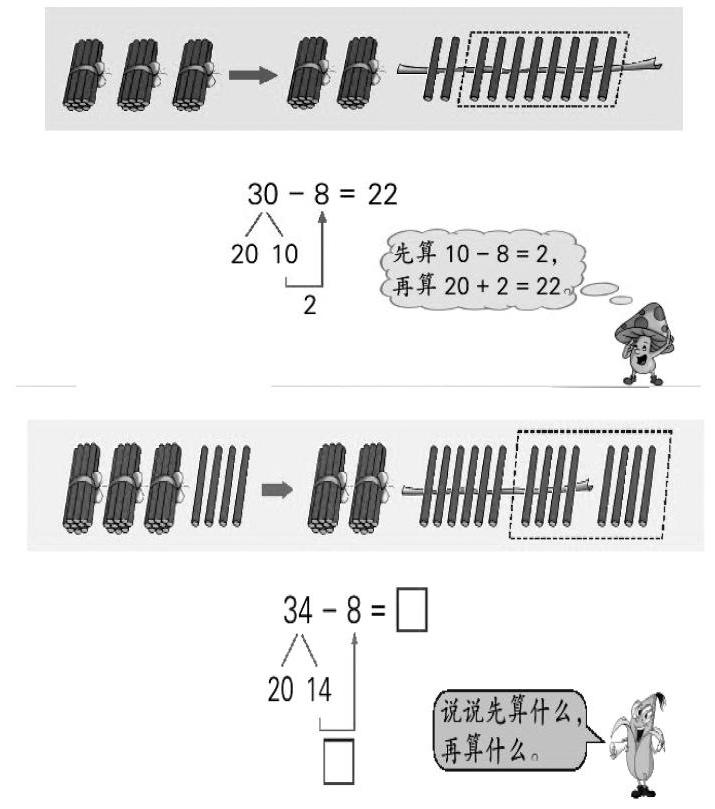
师:将一捆小棒拆开变成10根,就是将30分成了20和10。
师: 如果不摆小棒,你还会算吗?(先算10-8=2,再算20+2=22)
指名几人说说怎么算的。
这个片段的教学,主要是解决退位的原理和方法。低年级的学生,及时、适时的动手操作,对学生理解抽象、复杂的知识有着无可替代的作用。学生一边用脑思考,一边用手操作,一边用语言说清楚操作的过程,当学生能够将一道计算题说清楚的情况下,也必定能够理解其中的算理。在操作中说算理,便于学生建立起操作和计算的联系,所以教师在课堂上适当安排“说算理”步骤,要求学生将自己的思考过程说清楚,一方面能够迅速地实现口算,另一方面能够让学生明确算法。
【片段二】教学34-8
30-8大家已经会算了,那34-8呢?大家想想看,有困难也可以请小棒帮帮忙。
反馈如下:
方法一:
个位上4减8不够减,看成14-8=6,再把6和剩下的20合起来就是26。(分析)这种算法是前面学过的30-8的自然迁移。需要理清的算理是:14是哪里来的?20又是哪里来的呢?可以借助小棒,帮助学生理解:从4根小棒里面减去8根不够,可以拆开一捆小棒,将拆开的10根小棒和4根合起来就有了14根,剩下的2捆小棒就是20了,也就是将34分成了20和14。接下来从14根小棒里减去8根,剩6根,和2捆合起来是26根。
方法二:
30-8已經学过了等于22,那么34比30多4,所以得数也多4,在22上面加4就是26。
(分析)30和34都是被减数,低年级的孩子说总数更好理解。总数原来是30现在是34,增加了4,但减掉的还是8,所以剩下的得数也会增加4。
这种算法的算理比较难以表述,就不一定要让学生完全表达清楚,只要让学生意识到它就可以了,将要明确的算理蕴藏在具体的计算中。
方法三:
把34-8看成34-10=24,多减了两个再加上去,24+2=26。(板书:34-10+2=26)
方法四:
从34里面拿一个10来减8,等于2,再把剩下的24和2加起来等于26。
方法五:
把34-8看成34-4-4,34-4=30,30-4=26
(分析)以上三种算法,都和“凑整”策略有关。方法三中,为什么把8看成10来减?因为孩子觉得10算起来简单。教师可适时点拨:“可不是嘛!10无论算加算减都比其他数简单,所以才会有“凑十法”呀!不止是10,只要是整十数的计算都比较简便。”方法五中,教师可以追问几句:“34-4-4和原来的34-8意思一样不一样?都是从34里面减去几?”“34-8看成34-4-4有什么好处?看成34-2-6可不可以?”通过追问帮助学生理解为什么这样算,在算法和算理之间架起一座桥梁,使学生真正理解算理和算法之间的关系,让学生的数学运算从感性上升到理性的高度。
片断二的教学主要激发学生的创新意识,发散他们的思维,拓宽解题思路。小学数学计算教学的重点不仅仅是放在教给学生正确、基本的计算程序,教师更应该使学生掌握一系列的计算策略,包括凑整、补偿、分割、重新组合等。其中“凑整”策略是运用比较多的一种,因为学生对“整五数”“整十数”比较熟悉。在学生熟练地运用这些策略解决个位数计算的基础上,还可以将这些策略应用于两位数、三位数的更复杂的运算中。不管哪种运算策略,都要让学生搞清楚计算过程的依据和合理性,在师生对话、生生对话中,引发对“怎样算?”“为什么这样算?”“这样算有什么好处?”等一系列问题的思考。长此以往,学生不仅会逐步形成运算技能,还会将运算提升到思维的层面,这是运算能力发展的重要内容。
【片段三】自主优化算法
师:你们想了这么多方法,到底哪种方法比较简便呢?现在老师这有几道题,用你觉得简便的方法做做看: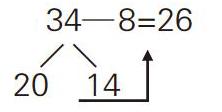
46-9
生1:我用的是把9看成10 的方法,46-10=36,再加上1等于37。
师:你为什么选这种方法?
生1:9很接近10,减去10 以后,只要再加1就行了。
师:确实很简便。
生2:我是先用的16-9=7,因为16-9=7我们学过了,再算30+7=37。
师:是啊,这两种方法都能很快算出得数。
52-6
师:52-6呢?
还是生1站起来说:老师,这题我没有把6看成10来算,因为6不接近10。我用的是12—6=6,6+40=46。
生3:我也是用的这种方法。
师:看来不少同学都喜欢用十位退1的方法,把 2看成12来减。这种方法正好把我们很熟练的20以内的口算用上了,所以我们更容易掌握一些。
(分析)教师不急于对各种算法进行评价,尊重学生自主的选择,保护学生自主发现的积极性。然后给学生一道题,46-9 ,学生可以按自己的经验选择不同的方法进行计算。 学生自然而然地筛选出两种方法:把9看成10来减,以及传统的十位退1,用16-9的算法。教师仍对这两种算法给予肯定,紧接着又出一题52-6,学生又在这两种算法中肯定了后一种,而这也是教材上要求学生掌握的算法。从循序渐进的角度来讲,20以内的口算退位减给这种算法做了铺垫,利于学生掌握;而从长远的角度来看,这种算法又是以后学习更复杂的笔算退位减的基础。
这个片段的教学告诉我们,在实施运算的过程中,会遇到多因素的情况,需要不同的思维方向、不同的解题思路和不同的解题方法。一题多解和多题一解出现在运算过程中是十分普遍的,一题多解体现了运算的灵活性,是激活解法的核心。一题多解的目的并不是一味强调“解法的多样化”,而在于思维的“多层次”,在于学生从众多的解法中比较反思、分析出解法的优劣,最终能够选择合理简洁的运算途径,这是运算思维达到一个新的高度的重要标志。
课改初期,我们在计算教学上走过弯路:过分注重算法的多样化。老师课堂上花费很多时间致力于算法的挖掘,思维快的学生能想出好几种,而一些思维慢的学生搞得眼花缭乱,无所适从,最终也不知道哪个方法最好。一段时间下来,学生的计算能力大不如以前,速度和准确率都不高。计算教学中一味追求计算技能的提高和过分强调计算方法的多样化,是两种极端,都是不可取的。缺少明明白白的说理和计算方法的提炼,必然导致算理不突出、算法不扎实,学生运算能力下降。
要提高学生的運算能力,在平时的教学中,必须要让学生真正搞懂为什么这样算,明确了算理和算法,就便于灵活、简便地进行计算,计算的多样性才有基础和可能。计算方法的多样化如体现同一层面的,没有很明显的优劣之分,可以遵循学生的个体意愿,让学生自由选择;有明显优劣之分的,教师要进行合理引导。数学中“算法最优化”的含义是要求在众多算法中寻找最简捷、速度快、不易错的方法,而不是你喜欢怎么算就怎么算。这一点,教师在课堂教学中要十分明确,要负责任地引导学生通过算理去比较、去评价,并使学生掌握那些公认的最佳的、最优的、最基本的算法,只有这样,才能更好地保证学生正确计算,提高他们的运算能力。
还要注意两点,一是强调算理的教学,并不等于每种算法都要让学生把算理表达出来,对于有的算理,小学生是难以表述的,只要让学生感悟就可以了。二是通常不需要在计算教学中把算理提出来进行专门的教学,而是把它蕴藏在计算过程之中,让学生在计算中明确这样算的道理。
【参考文献】
[1] 史宁中. 义务教育数学课程标准(2011年版)解读[M].北京:北京师范大学出版社,2012.
[2] 王光明,范文贵. 新版课程标准解析与教学指导—小学数学[J].教学教育学报,2015(5).
