学会转化 激活思维 解决问题
2018-08-07陈美娇
陈美娇
【摘要】在小学数学教学中,数学知识本身非常重要,但真正对学生以后的学习、生活和工作起长期作用,并使其终身受益的是数学思想方法。转化思想是数学思想的核心,是解决数学问题的一个重要思想。在教学中,始终紧扣“转化”这根弦,对提高学生的思维能力、分析问题和解决问题的能力是十分有效的。教师应把隐含在知识中的转化思想加以揭示和渗透,使他们能用转化的思想去学习新知识,分析并解决问题,让学生明确转化思想的作用,体会运用转化思想的乐趣,提高学生的数学素养。
【关键词】转化思想;激活;思维;解决问题
转化思想是数学中最普遍使用的一种思想方法,既是一般化的数学思想方法,也是攻克各种复杂问题的法宝之一。在小学阶段,学生经常面对新知识、新问题,需要从已有的知识和经验出发,采用恰当的转化手段把陌生问题转化为熟悉的问题,把复杂的问题转化为简单的问题,把未知转化为已知……在转化的过程中,学生通过学习尝试不同的转化方法,体会、领悟转化思想的本质,将带给学生成功的体验,这是助推思维迅猛飞跃的用不完的燃料。因此,如何在不同的数学内容教学中挖掘转化思想,适时向学生有机渗透,使学生通过提炼、总结、理解、应用等循环反复的过程中逐步感悟出数学知识、技能中蕴涵的转化思想,激活思维,是我们数学老师的一项重要任务。
一、纵向转化,化新为旧,解决问题
纵向转化,就是把面临的新问题转化为已经解决了的旧问题来处理,通过解决转化后的旧问题来解决新问题,这是转化思想中最常用的方法。例如:在探究《平行四边形的面积》时,我就适时引导学生进行纵向化归,提出问题让学生思考:我们学过哪些图形的面积计算公式?能不能将要学习的平行四边形的面积转化为已学过的哪个图形的面积来学习?学生很快就联想到了长方形。接着,我再让学生小组合作,动手操作,当学生通过“切割”“拼补”等方法将平行四边形转化成长方形后,我再引导学生观察发现:拼成的长方形跟原来的平行四边形有什么联系?从而推导出平行四边形面积的计算公式是:平行四边形的面积=底×高。最后,我再与学生达成共识:把不知道怎样求面积的图形转化为我们会求面积的图形,就是“转化”,转化是解决问题中常用的一种方法,将新问题转化为旧问题,就是化未知为已知,刚刚通过转化,我们将要学习的平行四边形转化成已学过的长方形,从而获得了新问题的解决方法。整个过程学生自己动手操作,自主探究,转化思想就深深嵌入学生的心中,试想,有了这节课做基础,后面再学习三角形、梯形和圆面积的计算公式时,学生就能对转化的思想方法运用自如了。
二、横向转化,化繁为简,解决问题
横向转化,就是把复杂、困难的问题转化为熟悉、简单的问题来处理,通过化繁为简的方法解决问题。有些数学问题比较复杂,学生刚看到题目时不一定马上就能发现其中的数量关系,这时就需要用一些方法将隐蔽的关系明了,使复杂的问题简单化。转化方法可以帮助学生使复杂问题简单化,从而更加清晰地发现问题、解决问题。数学问题解决过程中的转化,其形式多种多样,由一个问题转化为另一个问题,由复杂的问题转化为简单的问题,但总的转化路径是化繁为简、化难为易、化未知为已知。在教学中应突出转化思想在解题中的指导作用,注重转化思想的应用,使学生体悟数学思想。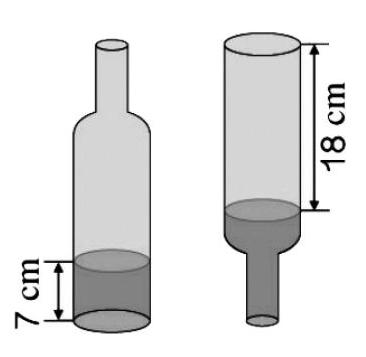
例如“一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?”教材呈现了一个装了小半瓶水的矿泉水瓶,下部是圆柱形,而上部是一个不规则立体图形。给出了瓶子平置时水的高度和倒置时无水部分的高度,要求这个瓶子的容积。这样的问题对于小学生来说很难直接解决,教师必须启发学生通过观察瓶子图,发现瓶子里的水倒置后,体积不变,水的体积加上18 cm高的圆柱的体积就是瓶子的容积。也就是把瓶子的容积转化为两个圆柱的体积,再引导学生列出算式: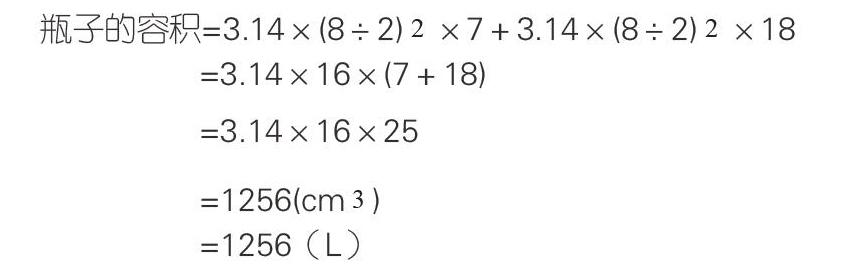
這样利用了体积不变的特性,把不规则的图形转化成规则图形来计算,化繁为简,清晰有序,使学生对转化的数学策略有更为深刻的理解和掌握。
三、同向转化,分解问题,解决问题
同向转化,就是把新问题转化为某一个或几个简洁处理的子问题,通过解决子问题,从而解决了新问题。修订后的人教版《义务教育教科书·数学》在编排时,注重学生综合运用知识能力的培养,每一册教材都出现一些综合性比较强的题目。知识是一点一滴的积累起来的,学生对于简单的问题能够从容处理,而对于多个知识点组成的复杂问题就一筹莫展、束手无策了。因此,遇到复杂的极易混淆的综合性问题时,教学时教师必须加强渗透数学教学中重要而又比较常用的一种教学策略,即“化整为零”,把综合性强的知识细化,逐一击破。如:“小明家住在电影院的正西650m,小冬家住在电影院的正东700m。周末两人约好去看下午3时放映的电影。两人下午2:45同时从家里出发走向电影院,小明每分钟步行70m,小冬每分钟步行65m,2:55两人能在电影院相遇吗?如果小明先到电影院后不停留继续向东走,从出发到两人相遇用了多长时间?相遇地点距离电影院有多远?”这道题的综合性较强,涉及方位、时间、速度和路程的数量关系等知识。教材所提的3个问题可以分别转化成容易理解的数学问题。第一个问题“2:55两人能在电影院相遇吗?”可以转化成“10分钟后两人是否都能到达电影院?”第2、3个问题是相遇问题中两个相关问题,可以借助下面的线段图帮助理解。
解答第2个问题时引导学生理解:“由于小冬家距离电影院更远,且速度更慢,则他所需要时间更长,如果他能按時到达,那么小明也可以。”接着引导学生根据:路程和÷速度和=相遇时间,列算式:(650+700)÷(70+65)=1350÷135=10(分钟)。再解答第3个问题时就比较容易,列式为10×70-650=50(m)。这样,把综合性较强的题目化为零碎的小问题,逐一转化,使知识点更易讲透,学生更容易更牢固地掌握知识。
四、逆向转化,换位思考,解决问题
逆向转化,就是当按照习惯的思维途径进行思考出现较难或较繁的情形时,从问题的另一面入手进行思考,从而解决问题。例如:设法求出下面两种物体的体积。
问题一出,同学A就说:将橡皮泥捏压成规则的长方体或正方体形状,再测量有关数据,就能求出它的体积。同学B就反问:那梨呢?梨是不能改变形状的。同学C:可是梨也没办法测量出有关数据啊?同学D:……当学生吵得正热烈,也没见得有好办法时,我就适时引导学生进行逆向化归,让学生思考:能不能借用我们前面认识的量杯或量筒来解决问题?再出示实验材料:量杯、马铃薯、水、记录单。请一组同学上台合作,进行实验。通过这组同学的实验,终于得出梨的体积是250立方米。我再引导学生归纳:这种求梨体积的方法就是“排水法”,适合求不规则物体的体积,用“排水法”求梨的体积,要注意记录数据和将梨完全浸没到水中。接着我再演示一次实验过程:先在量杯中倒入一定体积的水,读出并记录水的体积是200立方米;再将梨完全浸没在水中,读出并记录水和梨的体积是450立方米;最后计算出梨的体积:450-200=250(立方米)。小结时,我再告诉学生:因为梨无法转化成我们学过的某个立体图形,所以我们再用以前学习的立体图形的体积计算公式就计算不了梨的体积,这时,我们就得转化思路,换位思考,从问题的另一面入手思考,只有这样,才能找到解决问题的方法,正所谓“山穷水尽疑无路,柳暗花明又一村”。
实践证明,在课堂教学中教师如果能够以教材为媒介,坚持渗透转化思想,久而久之,学生就会将转化思想铭刻于心,运用自如,从而大大提高他们解决问题的能力。林碧珍老师将教学分为“三重境界”,分别是授人以“鱼”、授人以“渔”和“悟其渔识”。数学思想方法多达十几种,如果我们每位老师在课堂教学中都能加以渗透,那么这些思想方法就会慢慢转化为学生自身解决问题的方法,从而达到“悟其渔识”、“不教而教”的境界。
