一种新的变精度邻域粗糙集的精度值选取方法

沈 林

（莆田学院，福建 莆田 351100）

Ziarko提出的变精度粗糙集[1]是对Pawlak的经典粗糙集[2]的改进，通过引入参数β，提高粗糙集对抗噪音的能力，并且可以处理不一致数据，是粗糙集理论中的重要方法.针对经典粗糙集无法直接处理连续型数据，Hu提出了邻域粗糙集，并对变精度在邻域粗糙集中的应用进行了研究[3,4].在各种变精度粗糙集的模型中，参数β的取值通常依赖于先验知识，且主观性强，缺乏客观的依据.Zhang和Xue在文献5和文献6中用相似度分析不同参数β下的近似集接近目标概念的程度.本文依据此思路，给出一种针对变精度邻域粗糙集的精度取值新方法，通过计算在不同精度下近似集同目标概念的相似度，选择可以使相似度最高的精度.

1 基本概念

1.1 变精度邻域粗糙集模型

设DS=(U,C∪D,V,f)为一决策系统,u={x1,x2,…,xn}为论域空间，C、D分别是条件属性和决策属性，V为C∪D的值域，f是U×(C∪D)→V的映射.

定义1样本xi的邻域关系记为δ(xi)={xj|xj∈U,ΔA(Xi,xj)≤δ，其中 δ为邻域半径，A⊆C，ΔA(Xi,xj)表示在属性A下样本xi和xj的距离.

定义2引入参数 β(0.5≤β≤1)，有X⊆U，则有：

分别称为X关于β的下近似和上近似.

定义3xi对X的隶属度记为：

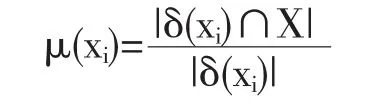
隶属度可以用来表示样本xi属于目标概念X的程度，取值范围为[0,1].本文依据所有样本的隶属度情况来选择参数β.

定义4近似集同目标概念相似度可使用下面的计算公式：

2 参数β的选取算法

为了改变以往的参数β取值缺乏客观依据，本文通过分析在不同的β下，近似集同目标概念相似度的变化情况，寻找可以使相似度最大的β.算法如下：

输入：决策系统DS=(U,C∪D,V,f)及目标概念X.

输出：更合理的参数β.

Step1：计算论域U在条件属性C下的划分U/C={X1,X2,…,Xn}；

Step2：计算每个样本xi的邻域对X的隶属度μi；

Step3：筛选出在[0.5,1]区间内的 μi，并去除重复值；

Step4：计算各个 μi下的下近似集 Rμi(X)；

Step5：计算各个 μi下的 Sμi(X,Rμi(X))；

Step6：找出 Sμi(X,Rμi(X))最大时的 μi；

Step7：结束算法.

3 示例

为了更加清晰地说明第二节的参数β选取算法，本节以表1的决策信息表举例，详细说明算法的运算过程.其中，U={x1,x2,x3,x4,x5,x6,x7,x8,x9,x10}，条件属性C={c1,c2,c3}，决策属性D={d}.

表1 决策信息表

可以看出决策属性D将U分为两部分：U/D={X1=(x1,x2,x3,x5,x6),X2=(x4,x7,x8,x9,x10)}.设邻域半径取0.1，每个样本在条件属性C的邻域如表所示：

表2 样本的邻域及对X1的隶属度

接下来依次计算每个隶属度下的下近似集，以及同x1的相似度，计算可得：

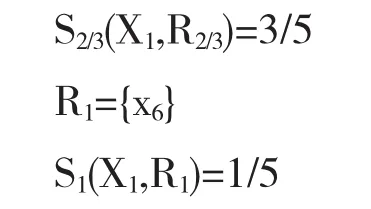
通过上面的计算，可以发现当μ=3/5时，得到的S3/5(X1,R3/5)=4/5最大，最接近目标概念X1，所以若目标概念为X1，应当将精度设置为3/5.

4 结束语

本文提出了一种用于变精度邻域粗糙集的精度值选取方法，可以解决以往精度值选取依赖先验知识，主观性强的缺点，可以使变精度邻域粗糙集模型更加具有客观性.本文选取的值可以使找出的下近似更加贴近目标概念，可以有效地减小变精度邻域粗糙集的边界域.