炮孔偏心不耦合装药爆破效应数值模拟*
2018-08-06汪海波王梦想
程 兵,汪海波,王梦想,宗 琦
(安徽理工大学 土木建筑学院,安徽 淮南 232001)
0 引言
不耦合装药结构广泛应用于光面爆破,以得到较平整的开挖轮廓面[1]。长期以来,有关不耦合装药的研究大多都假定炮孔和药卷圆心重合,即同心不耦合装药[2]。但在实际工程中,炮孔多是水平或竖向倾斜的,炸药会在重力作用下紧贴炮孔某一侧,形成偏心不耦合装药[3]。这时炸药爆炸能量并不是均匀地作用于炮孔周围岩石,耦合侧与不耦合侧的爆炸应力场和爆破破坏效应存在较大差异,特别是对如边坡光面和预裂爆破时,会导致需要保护侧的岩体产生破坏[4]。
蒲传金[4]通过测定3组偏心不耦合装药模型两侧的应变峰值,阐述了应力场分布存在偏心的现象,并根据声速降低率对比得出同心不耦合装药和偏心不耦合装药破坏效果存在差异;张建华等[5]基于超动态光测技术测得偏心不耦合装药爆炸应力场的动态演变历程,分析了该种装药结构下P波和S波与围岩损伤的关系;管少华[6]利用相似材料进行偏心不耦合装药爆破实验,得出爆后裂纹分布规律;李禹锡等[2]采用理论计算的方法从应力波干涉的角度分析了不同位置偏心不耦合装药爆破孔间的贯穿规律。以上研究大多都是开展模型试验进行的,较少采用数值模拟作为研究手段,本文利用ANSYS/LS-DYNA非线性动力分析平台,模拟不同不耦合系数时偏心不耦合装药炮孔周围的裂纹分布规律,以及同心不耦合装药和偏心不耦合装药爆破的爆炸应力场分布特征,为减少可能产生的破坏效应提供理论依据。
1 数值计算模型
在实际爆破作业中炮孔直径远小于其长度,在不考虑端部影响的条件下,可以将模型简化为单层网格模型[7]。利用ANSYS/LS-DYNA建立的数值模型如图1所示,采用圆形模型,其中模型体与炮孔的圆心重合,药卷紧贴炮孔下部。根据文献[6]中的模型试验,这里模型体直径为500 mm,药卷直径为7 mm,炮孔直径根据具体模型所选不耦合系数进行设定。炸药和空气采用ALE网格建模,单元使用多物质算法,即允许在同一个网格中包含多种物质,岩石采用Lagrange网格建模,岩石与炸药和空气之间的相互作用通过定义耦合算法来实现[8]。模型的四周施加无反射边界条件,以减小边界应力波反射的影响,这样更加接近周围岩体实际的受力状态[9]。
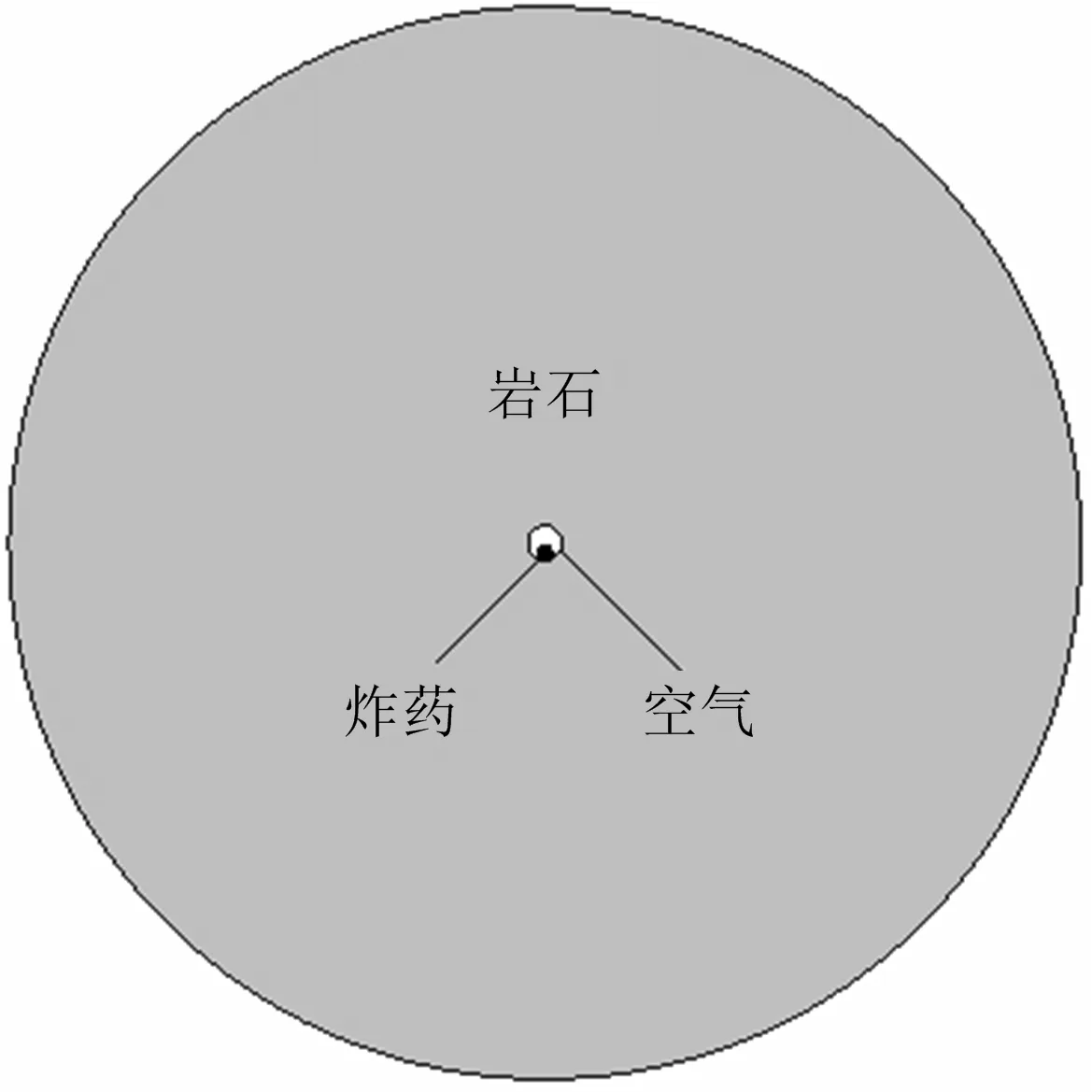
图1 计算模型Fig.1 Computational model
炸药采用*MAT_HIGH_EXPLOSIVE_BURN材料模型,状态方程通过关键字*EOS_JWL进行定义,用于描述压力与比容之间的关系[8],炸药材料及状态方程参数见表1。表中:ρe为炸药密度;D为炸药爆速;A,B为材料常数;R1,R2为无量纲常数;ω为定容条件下压力相对于内能的变化率;PCJ为炸药爆轰压力;E0为初始比内能。

表1 炸药材料及状态方程参数Table 1 The parameters of explosive material and state equation
空气采用LS-DYNA提供的空材料模型*MAT_NULL,状态方程通过关键字*EOS_LINEAR_POLYNOMIAL进行定义[10],空气材料及状态方程参数见表2。表中:ρ0为空气材料密度;E为单位体积内能;V为相对体积;C0,C1,C2,C3,C4,C5和C6为无量纲常数。

表2 空气材料及状态方程参数Table 2 The parameters of air material and state equation
岩石采用HJC材料模型,该模型是Holmquist在金属材料Johnson-Cook模型的基础上提出的,综合考虑了高静水压力、高应变率和材料的损伤效应,因此在工程材料冲击爆炸问题的数值分析中得到广泛应用[11],岩石材料参数见表3。表中:RO为岩石密度;G为剪切模量;A为内聚力强度;B为压力强化系数;C为应变率相关系数;N为压力硬化系数;FC为岩石单轴抗压强度;T为岩石单轴抗拉强度;EPSO为参考应变率;EFmin为岩石开裂的累积塑性应变;SFmax为特征化最大强度;PC为压垮临界静水压力;UC为压垮临界体积应变;PL为压实临界静水压力;UL为压实临界体积应变;D1,D2为损伤常数;K1,K2,K3为压力常数。
与岩石的抗压能力相比,岩石的抗拉能力非常差,而HJC模型本身不含有拉损伤模型[12],所以还要将岩石的抗拉强度设置为单元失效判据,利用关键字*MAT_ADD_EROSION进行定义[13]。
2 不耦合系数对裂纹分布的影响
针对直径为7 mm的药卷,数值计算时分别采用直径为7,9,11,12,13,14,15和16 mm的炮孔进行模拟,即装药不耦合系数为K1=1.00,K2=1.29,K3=1.57,K4=1.71,K5=1.86,K6=2.00,K7=2.14和K8=2.29,模拟结果如图2所示。

表3 岩石材料参数Table 3 The parameters of rock material
由于模型体和炮孔是同心圆,炸药紧贴炮孔下部,因此以炮孔中心为界,将模型均分为下部区域和上部区域,并分别命名为耦合侧与不耦合侧,如图2(a)所示。为了更好地说明裂纹分布情况,从不耦合侧左侧第1条裂纹起对裂纹进行标号,并在这里把裂纹尖端到炮孔壁的距离定义为裂纹长度,爆后炮孔周围的裂纹分布情况如图2(b)~图2(i)所示。具体裂纹长度见表4。
为了便于耦合侧与不耦合侧裂纹分布规律进行分析,对耦合侧与不耦合侧裂纹总长度、裂纹平均长度和最长裂纹长度及裂纹长度比值进行统计和计算,数据统计及计算结果见表5;得到裂纹长度、裂纹长度比值与装药不耦合系数关系如图3所示。
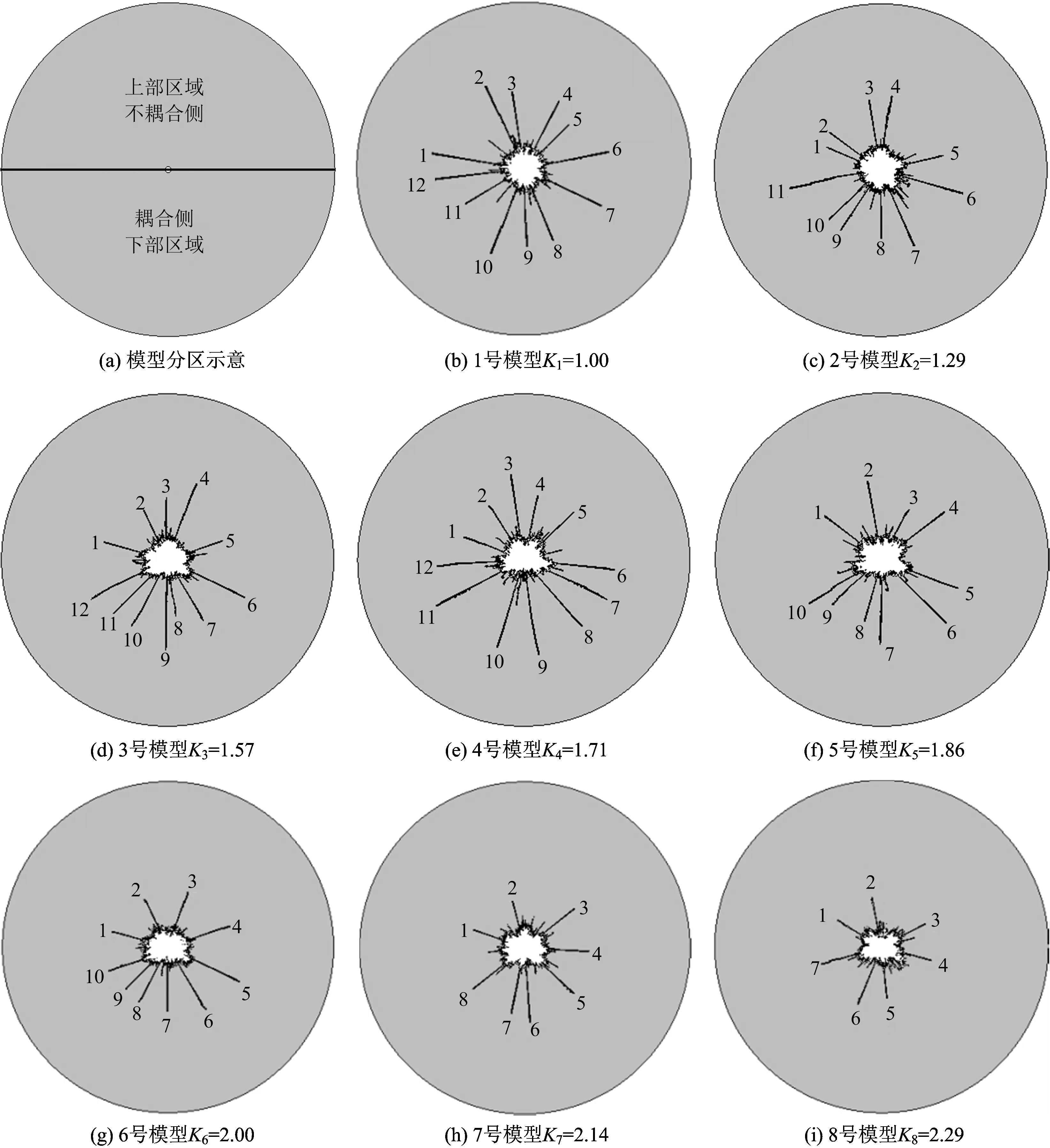
图2 模型分区及不同装药不耦合系数下裂纹分布情况Fig.2 The partition of model and the distribution of crack under differentdecoupling charge coefficients
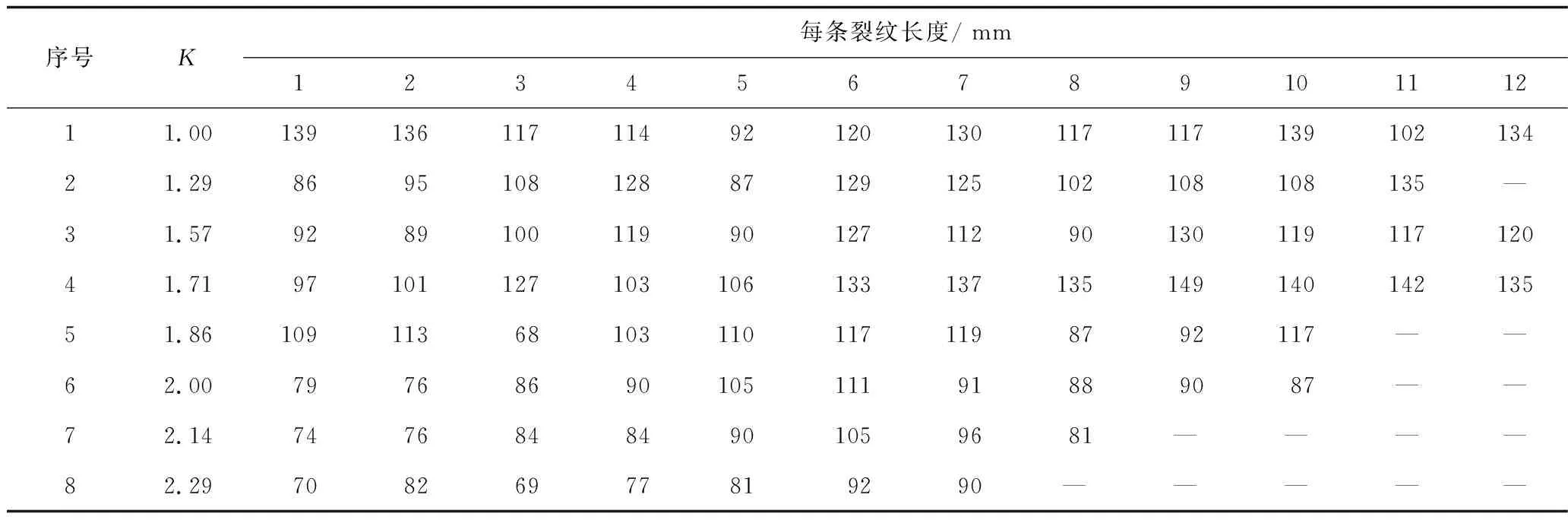
序号K每条裂纹长度/ mm12345678910111211.001391361171149212013011711713910213421.29869510812887129125102108108135—31.579289100119901271129013011911712041.719710112710310613313713514914014213551.86109113681031101171198792117——62.007976869010511191889087——72.1474768484901059681————82.2970826977819290—————
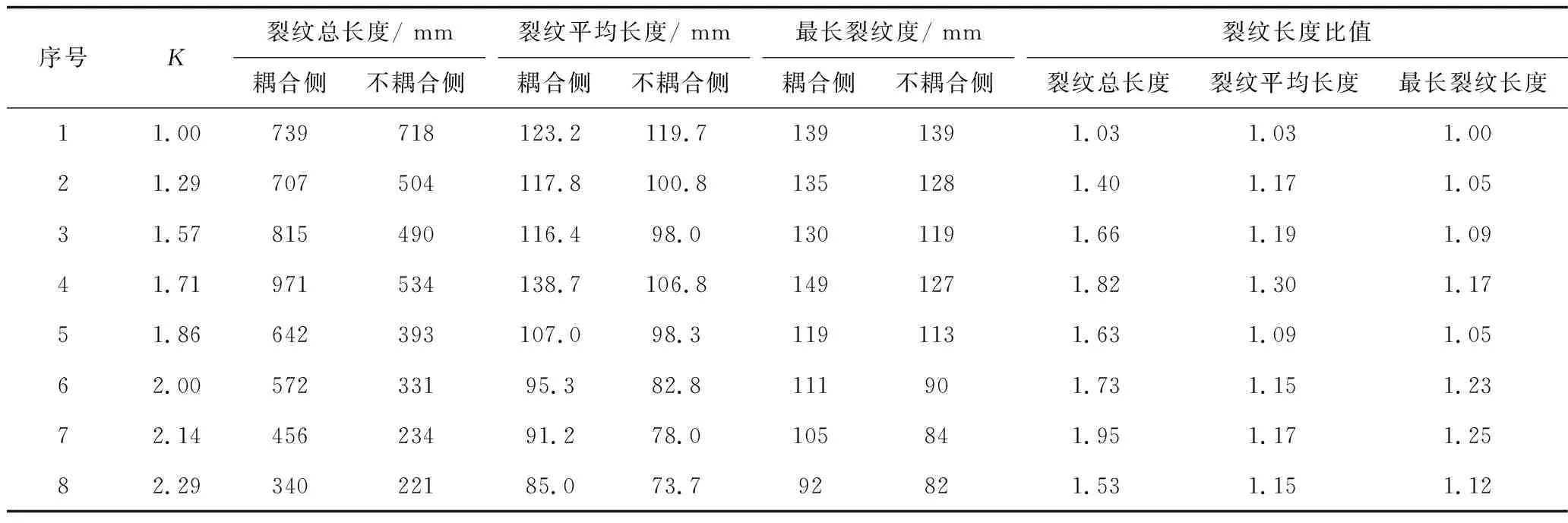
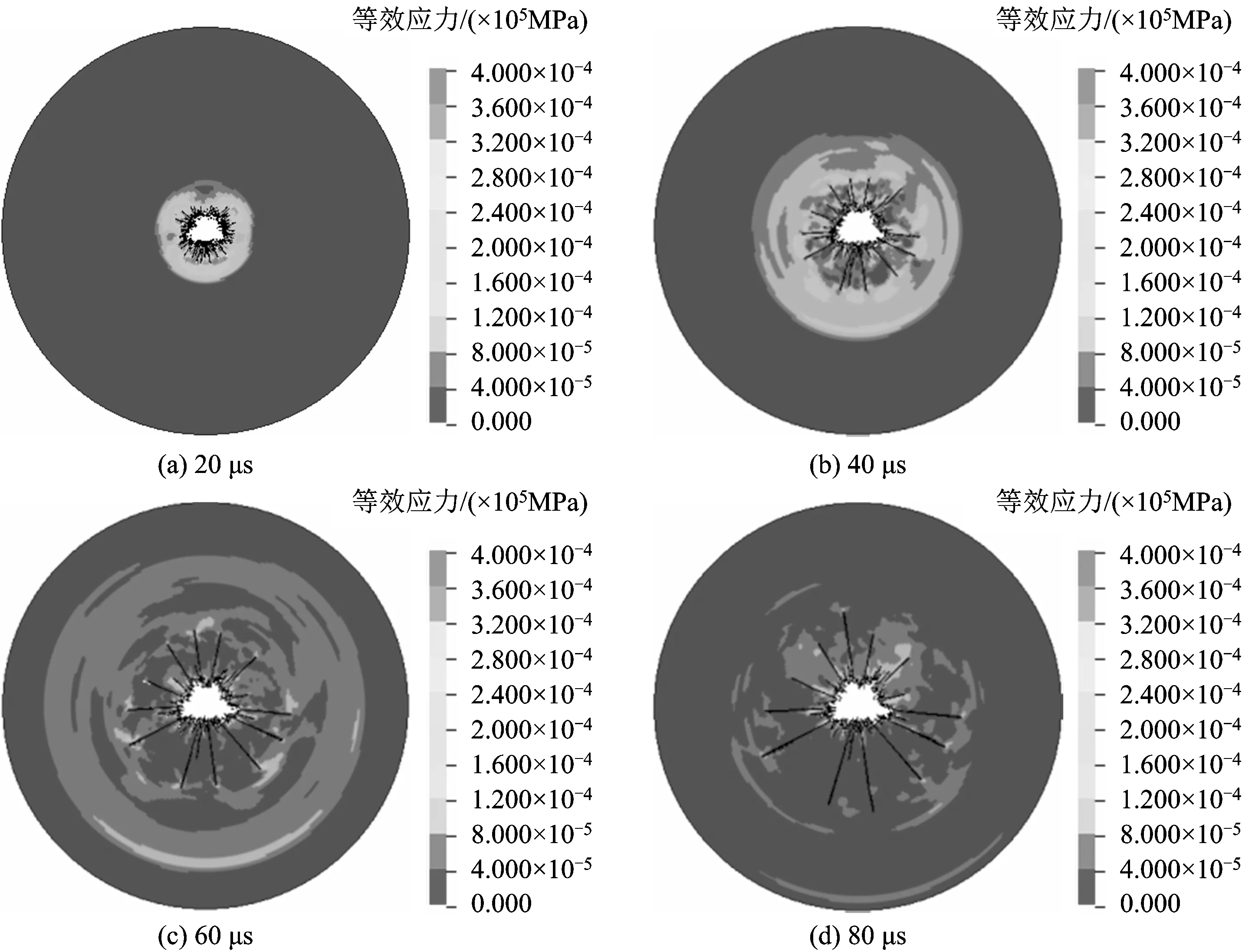
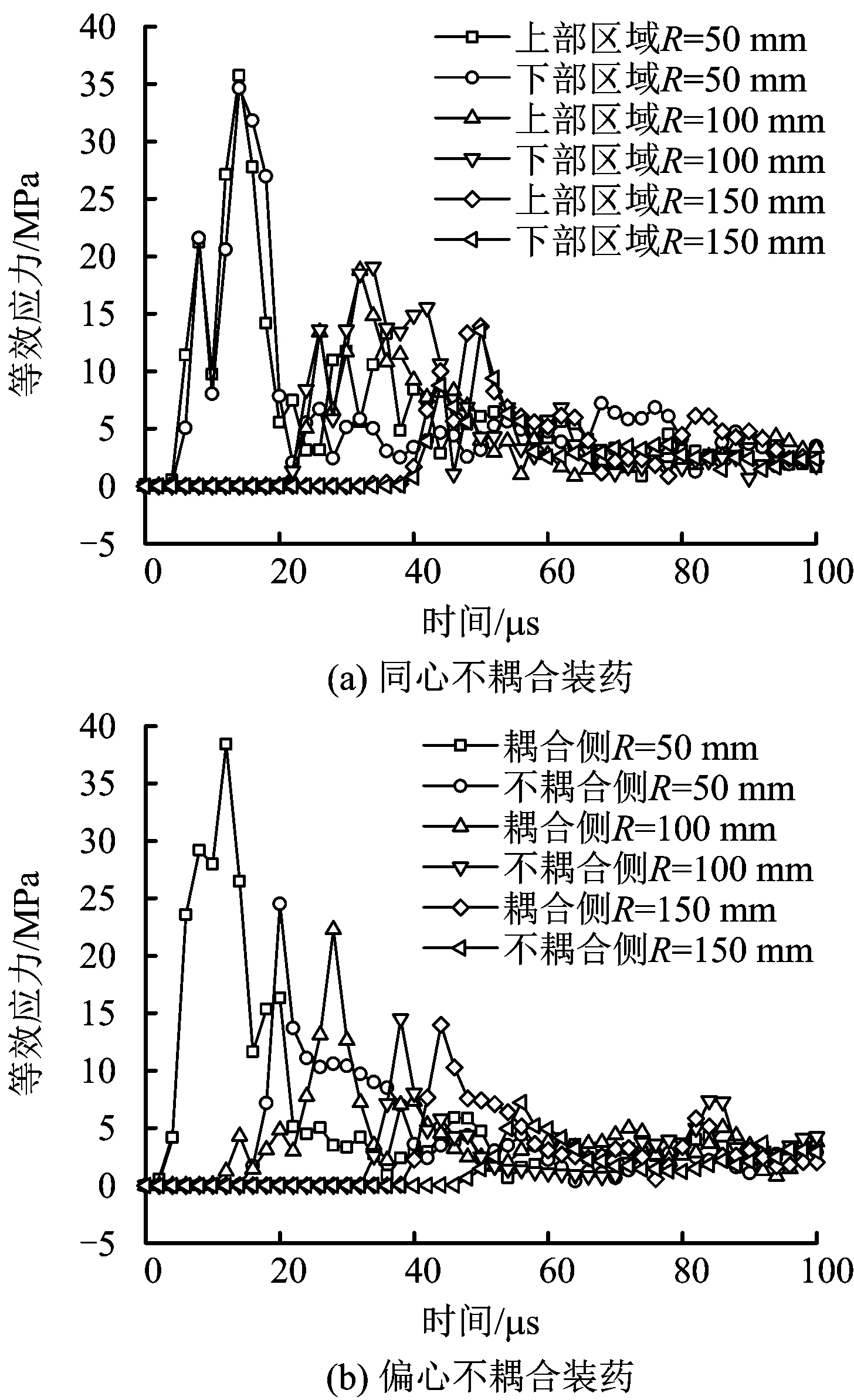
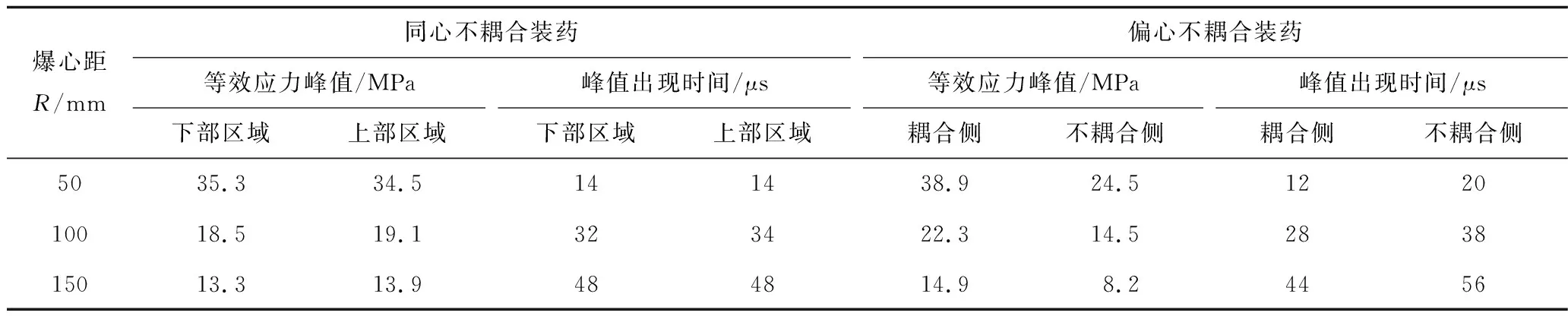
图3(a)~3(c)是两侧裂纹总长度、裂纹平均长度和最长裂纹长度随不耦合系数K变化曲线,可以看出对于K>1.00的任意一组偏心不耦合装药模型,耦合侧裂纹总长度、裂纹平均长度和最长裂纹长度始终大于不耦合侧。在1.0 图3(d)是耦合侧与不耦合侧裂纹总长度、裂纹平均长度和最长裂纹长度比值随不耦合系数K变化曲线,可以看出耦合侧与不耦合侧裂纹总长度、裂纹平均长度和最长裂纹长度的比值始终大于1.0,且变化趋势基本相同。随着不耦合系数的增大,开始先逐渐增大,在K=1.71出现一个峰值拐点,然后逐渐减小,而后又在K=1.88左右转为增大,并在K=2.14时再次出现一个峰值拐点。K=2.14时两侧裂纹总长度和最长裂纹长度的比值达到其最大值,但根据图3(a)~(c)不耦合系数大于1.88时炮孔周围整体的破坏效果大幅降低,实际工程中并不利于破岩。因此,在保证爆破破坏效果的条件下,可以认为K=1.71时两侧裂纹总长度、裂纹平均长度和最长裂纹长度的比值都达到其最大值,是优选的不耦合系数。 图3 裂纹长度和裂纹长度比值与不耦合系数关系Fig.3 Relationship between the length of crack and the ratio of crack length and decoupling charge coefficients 序号K裂纹总长度/ mm裂纹平均长度/ mm最长裂纹度/ mm裂纹长度比值耦合侧不耦合侧耦合侧不耦合侧耦合侧不耦合侧裂纹总长度裂纹平均长度最长裂纹长度11.00739718123.2119.71391391.031.031.0021.29707504117.8100.81351281.401.171.0531.57815490116.498.01301191.661.191.0941.71971534138.7106.81491271.821.301.1751.86642393107.098.31191131.631.091.0562.0057233195.382.8111901.731.151.2372.1445623491.278.0105841.951.171.2582.2934022185.073.792821.531.151.12 在实际光面爆破工程中,有采用改进偏心不耦合装药结构使药卷在炮孔中紧贴主爆区一侧[4],从而充分破坏主爆区岩体和降低围岩的损伤。根据以上分析,可以认为K=1.71为改进偏心不耦合装药的最佳不耦合系数。 等效应力云图能够反映炸药爆炸后岩石介质中爆炸应力场的动态变化过程[14]。由前所述,这里对不耦合系数K=1.71时同心不耦合装药和偏心不耦合装药爆炸应力场进行模拟,2种装药在不同时刻的等效应力云图如图4,5所示。同心不耦合装药形成的爆炸应力场在炮孔周围均匀分布,偏心不耦合装药形成的爆炸应力场则偏向于耦合侧。 图4 同心不耦合装药不同时刻等效应力Fig.4 Equivalent stress clouds of concentric decouple charge at different times 图5 偏心不耦合装药不同时刻等效应力Fig.5 Equivalent stress clouds of eccentric decouple charge at different times 为了对爆炸应力场进行更加直观的研究,在模型水平分界线的中垂线上,两侧分别在爆心距R=50 mm,R=100 mm和R=150 mm的地方取测点,通过后处理软件每2 μs输出一个等效应力值,得到如图6所示的同心不耦合装药和偏心不耦合装药两侧各测点的等效应力时程曲线,各个测点的等效应力峰值及峰值出现时间见表6。 图6 等效应力时程曲线Fig.6 Equivalent stress time history curve 从表6可以看出,在相同爆心距条件下,同心不耦合装药上部区域的等效应力峰值与下部区域基本相等,且等效应力峰值几乎在同一时刻出现;偏心不耦合装药不耦合侧等效应力峰值小于耦合侧,且不耦合侧等效应力峰值出现时间也滞后于耦合侧。 分析认为导致这种现象的主要原因是,药卷周围空气间隔对爆炸载荷产生了不同程度的缓冲和延迟作用。同心不耦合装药爆炸产生的冲击波在径向经空气间隔的缓冲,会降低冲击载荷强度并延迟载荷作用于孔壁的时间[15],但由于药卷和孔壁之间的空气间隔宽度相同,所以冲击载荷基本以相同大小同时作用于炮孔壁,此后冲击波衰减为应力波,两侧的应力波传播过程也基本相同。对于偏心不耦合装药,药卷在耦合侧紧贴孔壁或与孔壁之间空气间隔较小,药卷在不耦合侧与孔壁之间的空气间隔较大,较大空气间隔的缓冲作用会进一步降低冲击载荷的大小和冲击波延缓作用于孔壁的时间,使得作用于不耦合侧的冲击载荷在数值上小于和时间上滞后于耦合侧,此后冲击波衰减为应力波,不耦合侧应力波的等效应力峰值小于和峰值出现时间也滞后于耦合侧。 表6 等效应力峰值及等效应力峰值出现时间Table 6 The peak of the equivalent stress and the peak time of the equivalent stress 1)耦合侧裂纹总长度、裂纹平均长度和最长裂纹长度始终大于不耦合侧,不耦合系数为1.71时耦合侧与不耦合侧裂纹总长度、裂纹平均长度和最长裂纹长度的差值和比值都达到最大,K=1.71为改进偏心不耦合装药结构的最佳不耦合系数。 2)同心不耦合装药形成的爆炸应力场在炮孔周围均匀分布,偏心不耦合装药形成的爆炸应力场则偏向于耦合侧;由于药卷周围不均匀的空气间隔对爆炸载荷产生了不同程度的缓冲和延迟作用,偏心不耦合装药不耦合侧等效应力峰值小于耦合侧,且不耦合侧等效应力峰值出现时间也滞后于耦合侧。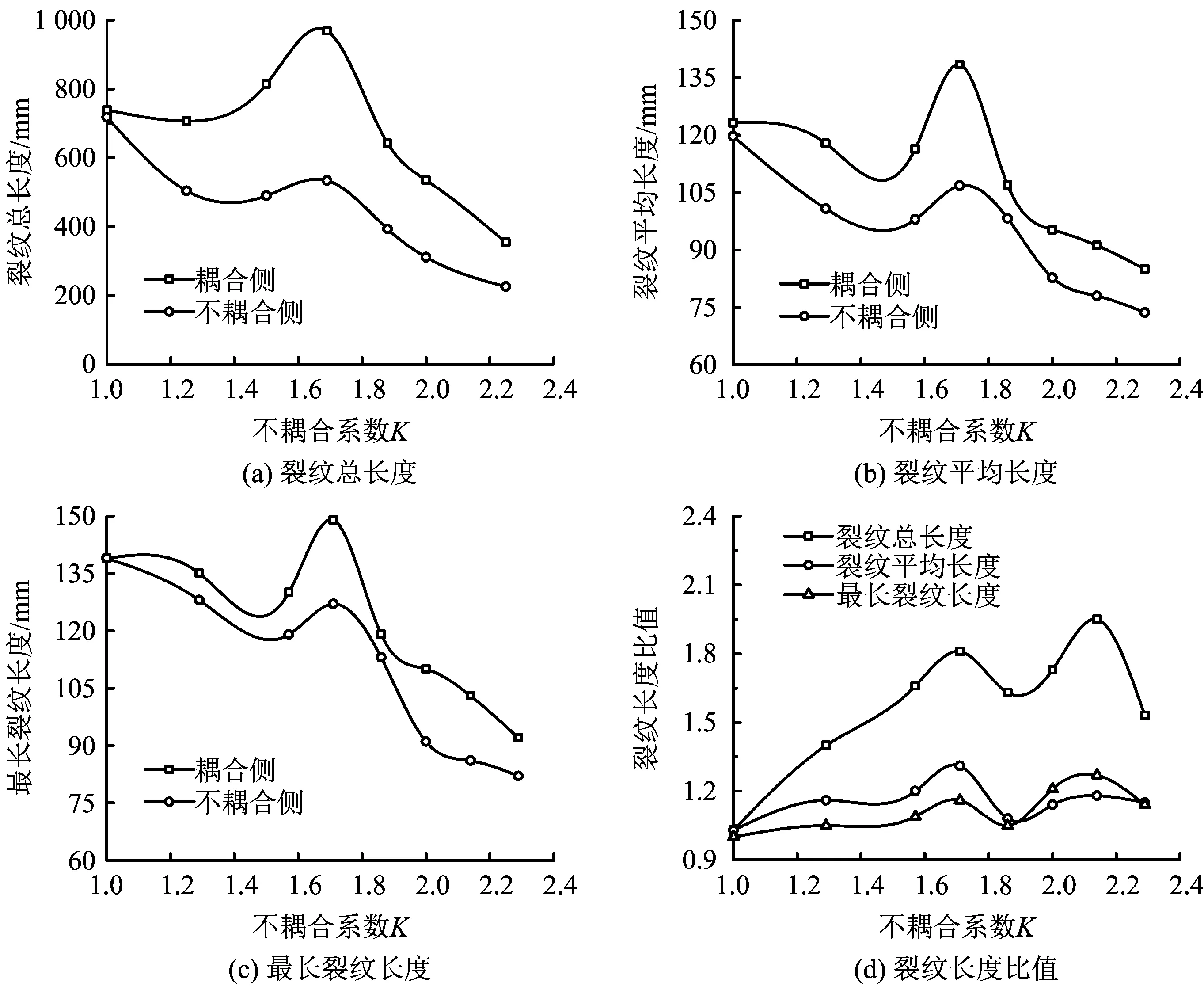
3 爆炸应力场模拟结果与分析

4 结论
