侧向载荷作用下X90管道局部屈曲研究*

张 晓，帅 健

(中国石油大学(北京) 机械与储运工程学院，北京102249)

0 引言

油气长输管道所处地理环境复杂多变，常会受到滑坡、泥石流等自然灾害所引起的侧向载荷的作用。另外，管道具有细长、薄壁的结构特性，因此极易在外载荷下产生较大变形而丧失稳定性发生屈曲甚至断裂破坏，从而引发管道事故，影响管道的安全运行[1-5]。此外，预防地质灾害也是当前油气管道完整性管理的重要内容和技术难点[6]。近年来，油气长输管道向大口径、高钢级方向发展，2007年发布的API Spec 5L-2007开始将X90列入管线钢系列，这对于X90钢在油气管道上的大规模投产具有里程碑意义。对X90管道局部屈曲的研究是其安全设计中必不可少的内容[7-8]。Wolodko等[9-14]对管道的局部屈曲响应进行研究，认为管材性能对管道屈曲行为具有十分重要的作用；Zimmerman等[15-17]采用有限元数值模拟方法并结合试验证实了这一观点；全恺等[18]采用ABAQUS有限元软件模拟分析了API-X80和API-X90管道在走滑断层位移下的屈曲变形响应规律，并探讨了管道径厚比、内压等参数对屈曲的影响，但并未定量分析幂硬化指数和屈服强度等材料参数对屈曲临界载荷的影响；王峰等[19-20]采用有限元模拟讨论了管道几何参数和初始缺陷对于X70管道屈曲失稳时屈曲模式和屈曲临界载荷的影响，但其所研究的管道为小管径，同时也未定量分析管径和材料参数等对于屈曲临界载荷的影响，因此，得出的结论对于X90大口径管道的适用性还有待进一步考证。

虽然众多学者对管道在不同载荷下的屈曲行为进行了相关研究，但针对X90大口径管道的局部屈曲研究较少，尤其是定量探讨材料参数与屈曲临界载荷之间的关系的研究更为鲜见。针对上述问题，本文通过采用有限元数值方法，对受侧向载荷作用下的X90管道的局部屈曲进行研究，详细探讨管道几何参数、材料参数对管道抗屈曲能力的影响，为X90管道设计、大规模投产提供理论基础和依据。

1 有限元数值模型

1.1 网格划分

采用ANSYS有限元计算软件中的APDL语言，建立X90管道屈曲数值模型。为了更清楚地观察管道整体屈曲模态，不宜采用对称模型，本文建立的有限元模型为管道的全模型。选用壳单元181可大大减少节点数量，从而提高计算效率。采用节点生成的方式进行建模，先在环向方向建立一圈节点，然后沿轴向方向拖拽复制，即可实现模型的网格划分。模型的网格数越多，计算结果越精确，但是耗时长；若网格过于稀疏，耗时少但影响计算精度。为保证计算结果的收敛性以及计算量的合理性，对管道环向和轴向网格尺寸和单元个数进行优化，确定了各方向网格最佳尺寸。图1为有限元模型网格划分示意图。

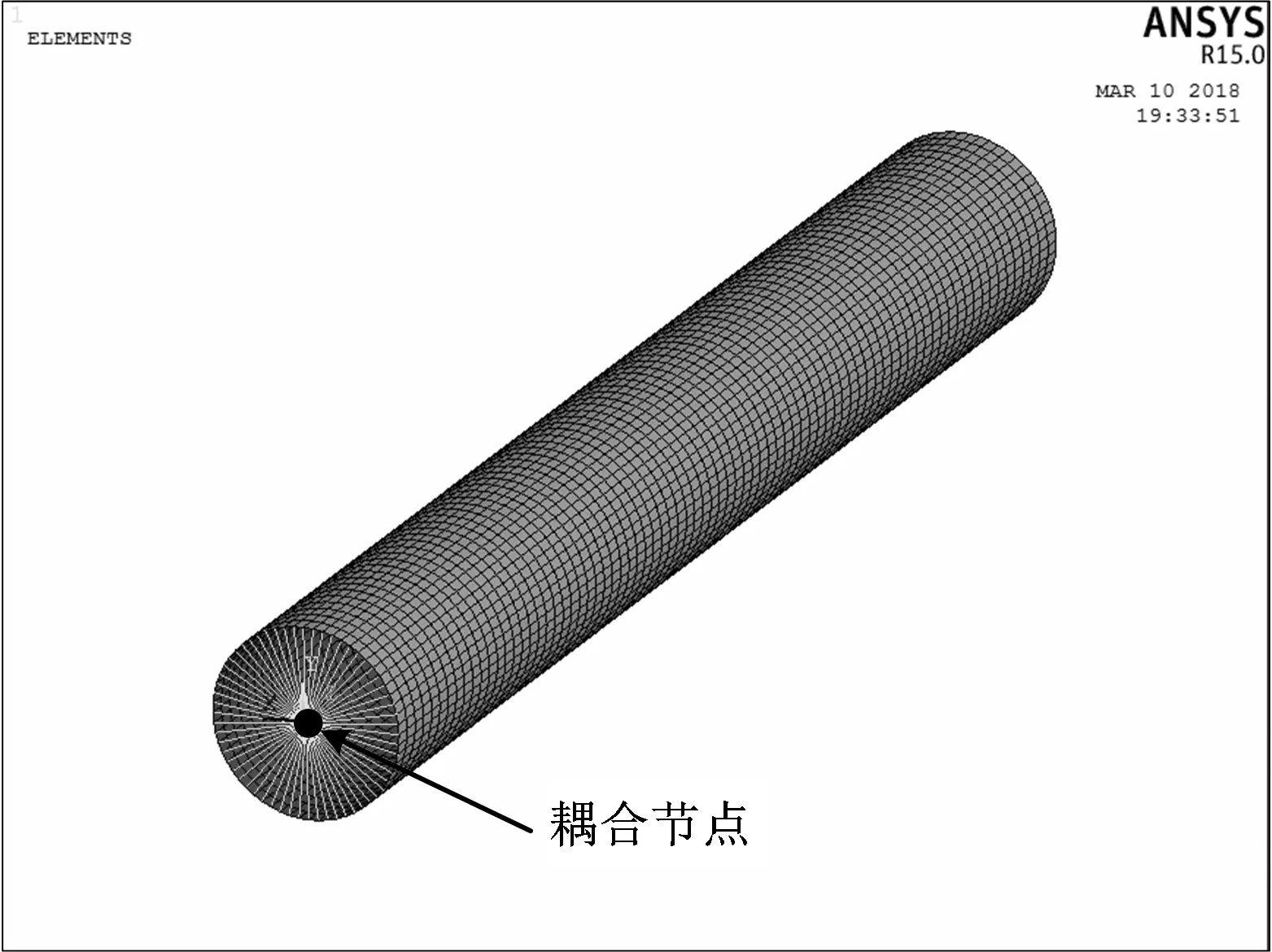
图1 管道有限元模型Fig.1 Finite element model of pipeline

1.2 边界条件及求解算法

该模型的载荷及边界条件为：管道一端夯实牢固，该端部的所有节点全约束；另外一端采用188号梁单元进行节点耦合，以施加弯矩载荷。求解分2个载荷步进行，第一步在管道内表面施加均布内压载荷，第二步在管道的自由端耦合节点施加弯矩。采用弧长法进行模型的求解。

1.3 材料模型

Ramberg-Osgood模型能够较好的模拟管道的材料特性，在工程上应用十分广泛，其表达式为：

式中：ε为真实应变，mm/mm；εy为屈服点的弹性应变，mm/mm；εy=σy/E，E为弹性模量，MPa；σy为屈服强度，MPa；σ为真实应力，MPa ；n为幂硬化指数；α为硬化系数，等于屈服点的塑性应变与屈服点的弹性应变之比，屈服点的塑性应变取0.2%。

在实验室加工X90管材试件，并进行单轴拉伸试验，实验完成后，采用上述R-O模型进行拟合得到材料的真实应力应变曲线如图2所示。得到管材参数为：弹性模量E=210 GPa；屈服强度σy= 625 MPa；幂硬化指数n为22。本文的有限元模型采用该材料应力应变曲线进行计算。

图2 X90管材的真实应力应变曲线Fig.2 Stress-strain curve of the material

2 屈曲模态分析及临界载荷确定

图3为管道受弯矩作用发生屈曲的过程中不同时刻管道的轴向应力示意图。从图3中可以看到，随着弯矩的增大，管道逐渐发生变形，当弯矩达到某一临界数值(图3(c))，管道发生屈曲失稳，局部屈曲位置变形最大，产生明显的皱褶，这是由于管道受到内压和侧压作用时，管道中段的弯矩最大，因此首先在管道中段发生塑性屈服。管道屈曲时，管道的最大轴向应力位置出现在管道中段屈曲附近，达到751 MPa，远大于管材的屈服强度。管道发生失稳后，受到弯矩的继续作用，随着管道挠度的变大, 屈曲也越来越明显，这个阶段称之为后屈曲阶段。

图4为有限元计算得到的耦合节点载荷位移曲线。从图中可以看到，初始阶段该节点弯矩随轴向位移的增大而快速上升，当轴向位移达到16.01 mm时，弯矩强度达到顶点，约8 061 kN·m。此后，随着位移的继续增大，载荷强度会随之下降。这是由于管体在载荷达到最强时发生了结构的屈曲失稳，造成了弯矩瞬间的下降，管体随后进入了后屈曲变形。载荷位移曲线的卸载点所对应的载荷就是管道的屈曲临界载荷。

图3 管道的屈曲变形示意Fig.3 Diagram of buckling deformation of pipeline

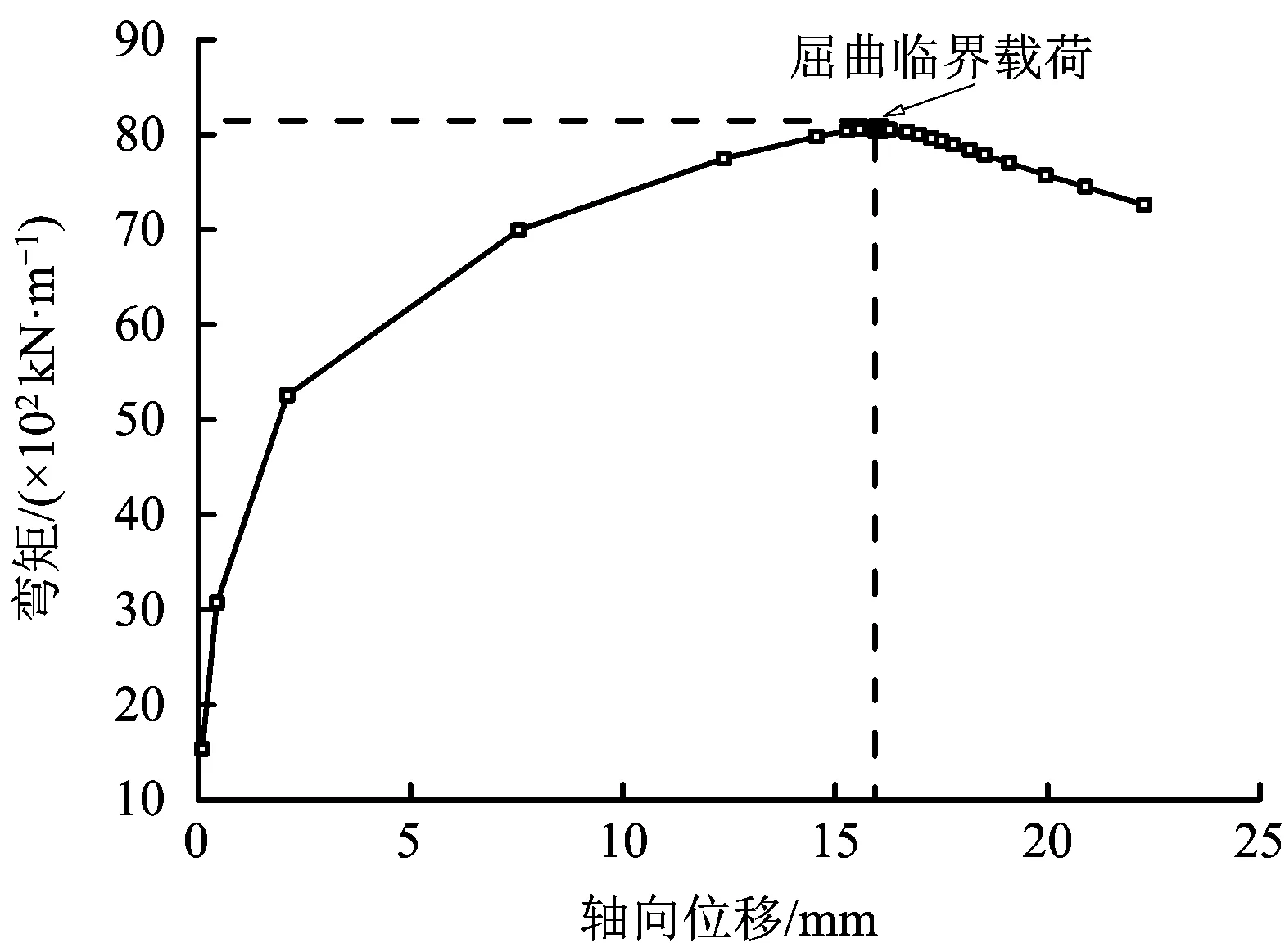
图4 耦合节点弯矩-轴向位移曲线Fig.4 Moment-axial displacement curves of coupling nodes

3 屈曲临界载荷影响规律

管道发生屈曲失稳与屈曲临界载荷密切相关，其与管道的直径、壁厚、内压以及材料参数密切相关。因此有必要分析这些因素对管道的屈曲临界载荷的影响，从而通过控制相关关键参数提高管道的抗屈曲能力，为管道设计提供一定的依据。采用上述有限元模型，计算了不同管道尺寸、操作压力以及材料参数条件下的管道屈曲临界弯矩，并分析了其随这些参数的变化规律。

3.1 管径的影响

管径影响管道的环向应力水平，还影响管道刚度，从而与管道抗屈曲变形能力直接相关。为了探讨管径对屈曲临界弯矩的影响，计算了当壁厚为10.3 mm，内压为6 MPa，屈服强度为625 MPa，幂硬化指数为22时，管径分别为720，810，1 016，1 219和1 422 mm下不同管道的临界屈曲弯矩，得出其与管径的变化关系图，如图5所示。从中可以看出，管道的屈曲临界弯矩随着管径增大而增大。

图5 管道屈曲临界弯矩随管径的变化规律Fig.5 Curves of the buckling critical bending moment with pipe diameter

3.2 壁厚的影响

壁厚直接影响管道的刚度，是管道抵抗变形的能力的重要因素。相关计算参数为：管径1 016 mm，内压6 MPa，屈服强度625 MPa，幂硬化指数22，壁厚取8～16 mm。计算不同壁厚下管道屈曲临界弯矩，并绘制屈曲临界载荷随壁厚的变化曲线，如图6所示。从图6中可以看出，在其他参数相同的情况下，随着壁厚的增加，屈曲临界弯矩线性增加，即壁厚越大，管道的抗屈曲能力越强。因此，在地质灾害频发地段，有必要适当增大壁厚，提高管道抵抗屈曲能力。

图6 管道屈曲临界弯矩随壁厚的变化规律Fig.6 Curves of the buckling critical bending moment with wall thickness

3.3 内压的影响

长输管道通常带压服役，内压影响管道的刚度和环向应力水平，因此有必要考虑内压对管道屈曲临界载荷的影响。有限元计算参数：管径1 016 mm，壁厚14.3 mm，管材X90，内压分别取值1～16 MPa，计算得到了管道屈曲临界弯矩随内压的变化规律如图7所示。可以看出，管道的屈曲临界弯矩随内压的增加呈现先增大后减小的规律。这是由于当管道内压较小或者无内压时，管道刚度较小，因此抗屈曲变形能力较差；内压增大，管道刚度随之增大，屈曲临界弯矩增大；而内压增加到一定程度时，随着内压的继续增大，管道的环向应力也随之增大并占主导作用影响了材料的切线模量，从而导致屈曲临界载荷减小。因此在特殊管段，根据管道实际运行状态，使管道在合适的内压范围下运行，对于提高管道的安全具有重要的作用。

图7 管道屈曲临界弯矩随内压的变化规律Fig.7 Curves of the buckling critical bending moment with pressure

3.4 材料参数的影响

管道受到侧向载荷的作用发生局部屈曲时，其屈曲位置局部区域应力大于屈服强度，处于弹塑性失效状态，具有较强的材料非线性，因此有必要考虑材料参数对管道的屈曲临界载荷的影响。管道材料参数包括幂硬化指数、屈服强度以及拉伸强度，已知其中两个参数即可确定材料的性能，本文考虑材料的屈服强度和幂硬化指数对屈曲临界载荷的影响。

首先考虑幂硬化指数的影响，有限元计算参数为：管径1 016 mm，壁厚14.3 mm，屈服强度固定为625 MPa，改变幂硬化指数的取值，计算了内压工况分别为8，12，15和18 MPa时管道的屈曲临界载荷随幂硬化指数的变化规律，如图8所示。从图8中可以看到管道的屈曲临界弯矩随幂硬化指数变化受管道内压的影响。当n<24时，随幂硬化指数n的增大而减小，且减小趋势逐渐减弱；当n≥24时，屈曲临界载荷不受n的影响。同时，内压越大屈曲临界载荷随减小趋势越明显，这是因为内压为18 MPa时，管道的环向应力已超过材料屈服强度，极大的减小了管道抗变形能力。因此，在工程应用中，在特定运行压力下，选取合适的幂硬化指数对于提高管道屈曲临界载荷、预防管道屈曲失稳具有重要意义。

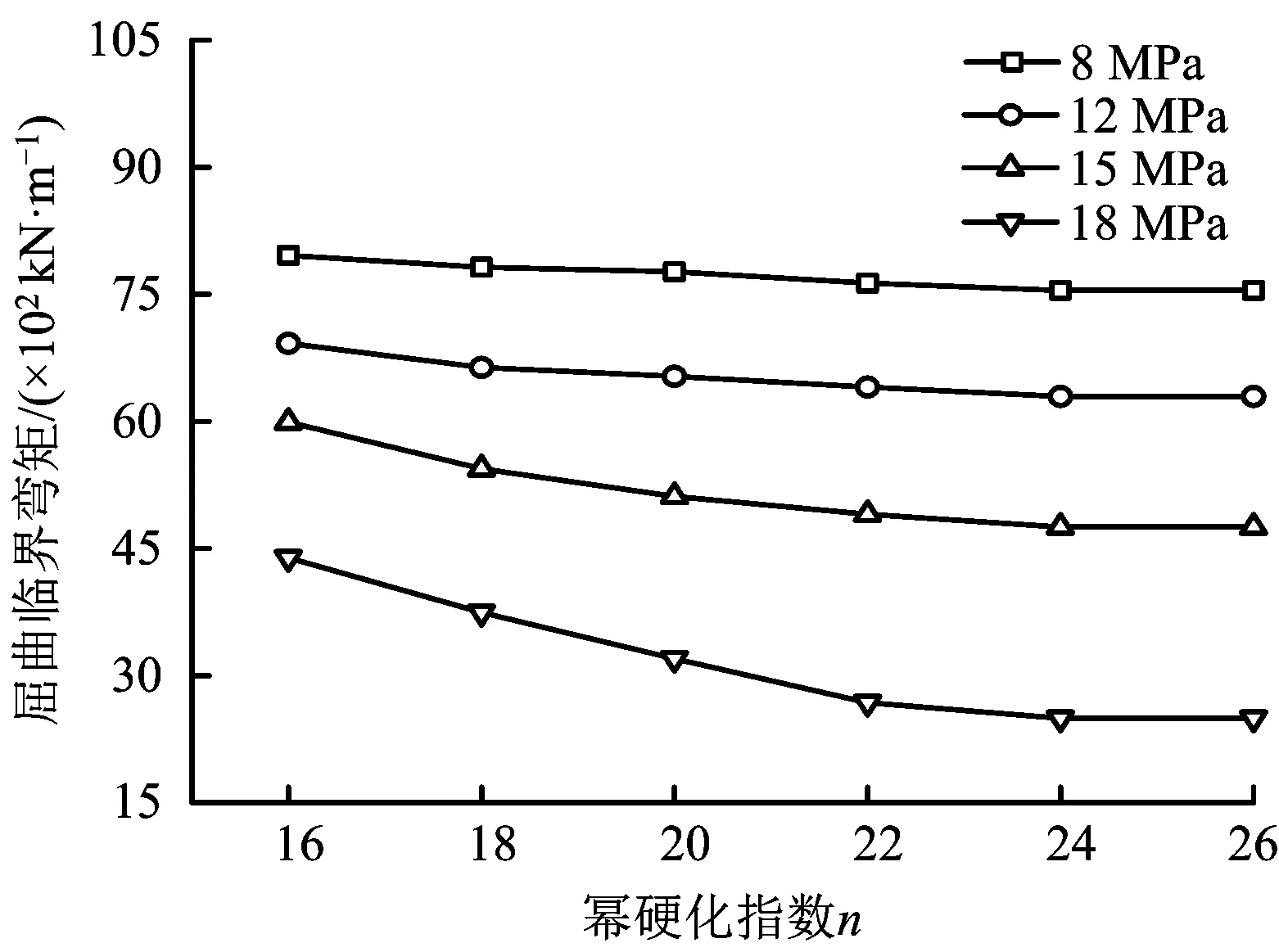
图8 不同内压工况下管道屈曲临界弯矩随幂硬化指数的变化规律Fig.8 Curves of the buckling critical bending moment with yield ratio and pressure

同理，考虑材料的屈服强度的影响。图9为管径1 016 mm，壁厚14.3 mm，内压12 MPa，屈服强度分别为595，625和655 MPa时，管道屈曲临界弯矩随幂硬化指数的变化规律。从图9中可以看出，幂硬化指数一定时，随着屈服强度增大，屈曲临界弯矩也随之增大。因此，提高管材的屈服强度在一定程度上有助于提高管道抗屈曲变形能力。

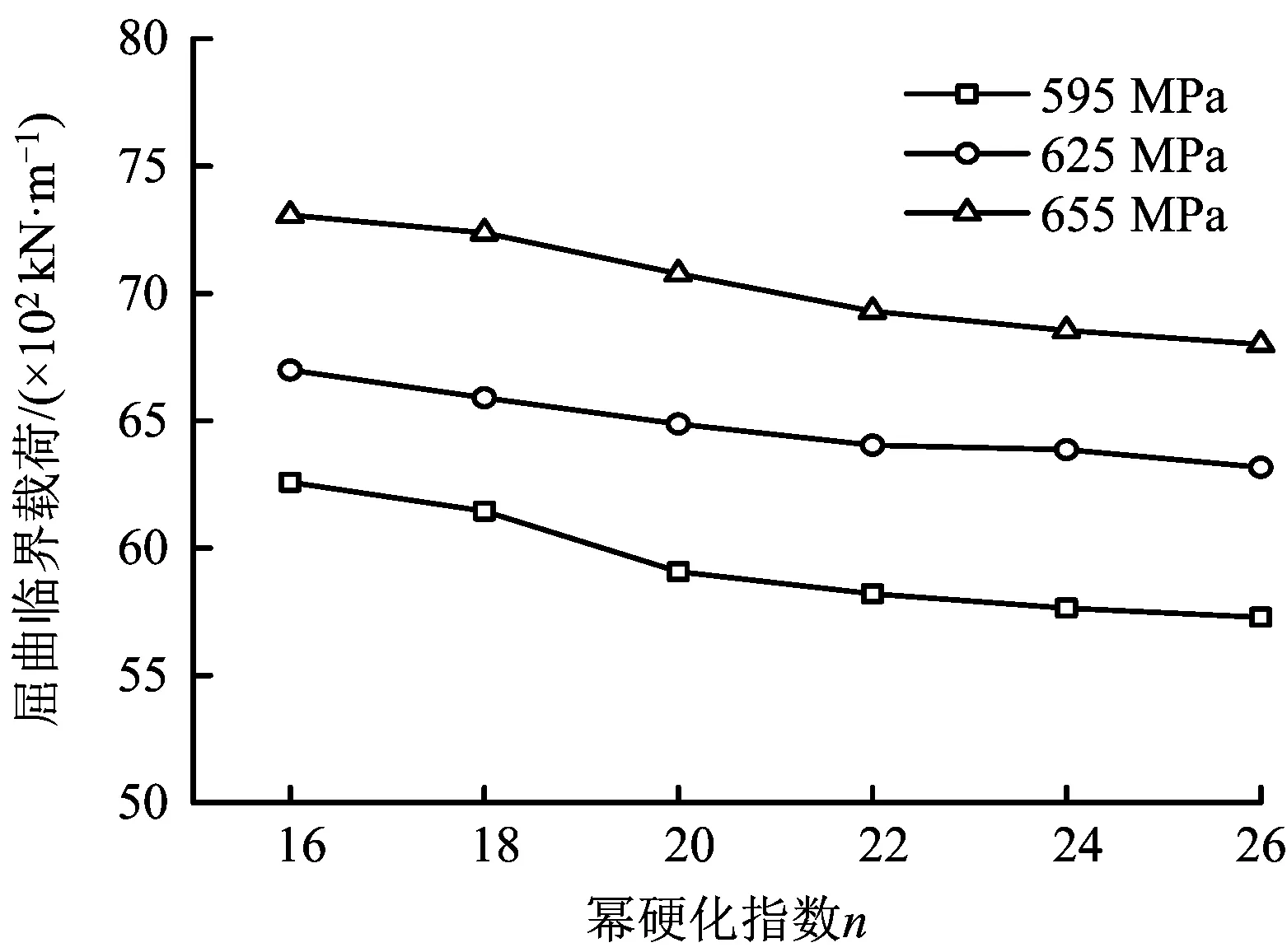
图9 管道屈曲临界弯矩随幂硬化指数与屈服强度的变化Fig.9 Curves of the buckling critical bending moment with yield ratio and yield strength

4 结论

1) 采用节点耦合的方式建立了X90管道受到侧向载荷作用下局部屈曲数值计算模型。通过计算发现，管道在侧向载荷作用下局部发生屈曲时，屈曲区域管壁应力较大，远超过管材屈服强度。

2)综合研究了管道尺寸参数、操作压力以及管材参数对X90大口径管道局部屈曲临界载荷的影响规律，结果发现：屈曲临界载荷随管径以及壁厚的增大而增大；随内压的增大而先增大后减小；n<24时，随幂硬化指数的增大而减小，且管道内压越大其减小趋势越明显；n>24时，管道屈曲临界弯矩不再受n的影响；管材屈服强度的提高在一定程度上提高的抗屈曲能力。

3)建议X90管道设计和投产时，在地质载荷频发地段可以通过加大局部管段的壁厚或控制管道运行压力来提高管道的安全性。在符合X90设计标准的情况下，适当控制管道钢的材料参数可以提高管道的抗屈曲变形能力，有效减少管道屈曲破坏事故。