初探孔边应力计算模型

王文璟，左斌峰，冯 超

（铜陵职业技术学院，安徽 铜陵 244000）

一、前言

近年来，点支承玻璃幕墙因其轻灵飘逸的风格，得到了众多建筑师的青睐，应用越来越广泛。但是在使用点支撑玻璃幕墙的过程中，特别需要注意孔边受力性能对玻璃幕墙寿命的影响[4,7]。国外的一些实验表明：支承处玻璃受拉是引起点支玻璃结构破坏的主要原因，而且四点支承玻璃的破坏多数情况下出现在孔边[3]。另外，由于孔边加工及安装施工会增强孔边玻璃强度的离散性，使得由于孔边受力性能引起结构破坏的概率进一步增加[1,2]。因此，孔边受力性能的研究是点支玻璃应用中需要注意的关键问题，对该问题的研究对于点支玻璃的工程应用有重要指导意义。

分析孔边应力的有效工具是有限元方法，但是有限元计算能否反映真实的孔边应力及变形状态，完全取决于孔边的边界条件及接触条件的设定和选取，即数学模型对实际模型的近似程度。因此，建立合理的孔边有限元计算模型是分析点支玻璃孔边受力性能的关键问题。本文即针对该问题进行研究，首先分析了目前常用的两种建模方式 （简化模型和理想模型）的优缺点，在此基础上，进一步提出一种半简化模型。相比完全简化模型，本文提出的半简化模型考虑了孔边材料的部分接触作用，相比理想模型，半简化模型中省略了影响较小的材料接触因素，因此所提出的模型在计算效率和计算精度方面取得了很好的平衡，更适合工程应用。最后通过实际的算例对模型进行了验证。

二、孔边应力有限元计算模型

有限元计算模型包含玻璃板、起缓冲效应的密封垫层和金属连接件（驳接头）三个部分。目前常用的描述上述三个部分的模型主要有两种。第一种是简化模型，即认为材料整体一起变形，在两两接触面上的节点是共用的，接触面既不会脱离，更不会发生相对滑动。这钟模型可以简化计算，耗用计算资源少，计算速度快。其缺点是对实际孔边的状况模拟不够，特别是使孔边的变形能力小于实际状况，这可能会导致较大的应力集中效应，使得计算结果偏大。采用这种模型，在垂直于板面的荷载作用下的孔边变形示意图如图1所示。

图1 采用简化模型，在垂直于板面的荷载作用下的孔边变形示意图

第二种是理想模型，即考虑这三个组成部分之间的接触性质，玻璃板依靠与密封垫层的接触来提供对自身的约束，密封垫层依靠与玻璃板及驳接头的接触来提供自身的约束，金属连接件依靠与垫层的接触来提供自身的约束，也就是说三者通过互为依赖的接触来保证整个结构体系的静力稳定。但是，理想模型在实际建模过程中较难实现，因为这其中存在两对接触关系，分别是玻璃板和垫层的接触，及金属连接件和垫层的接触。独立处理这两对接触关系并不困难，但问题在于这两对接触均涉及到同一垫层，而有限元计算程序没有办法动态考虑这两者之间的互相影响，而同时整个体系需要接触来提供约束，这使得调整初始接触条件变得较为困难。当初始接触条件未能反映实际情况时，系统会出现刚体运动，从而导致计算无法进行。

综合考虑上述两种模型的优缺点，本文提出一种半简化有限元模型，在该模型中，保留金属连接件和垫层的接触关系，忽略玻璃板和垫层的接触关系。由于玻璃板和垫层的接触更多表现为摩擦滑动，其对孔边的整体状态影响较小，因此选择忽略它们之间的接触关系。由于接触问题是高度的状态非线性行为，需要较大的计算资源，因此只保留一对接触关系可以节省计算资源，提高计算速度，另外，相比与完全简化模型，保留了金属连接件和垫层的接触关系，可以使得计算模型更接近实际情况，提高计算精度。使用半简化模型，在垂直于板面的荷载下的孔边变形示意如图2所示。

三、仿真算例

算例中所用钢化玻璃的尺寸为：长2000mm，宽1000mm，厚15mm，孔边距100mm。金属连接件为沉头驳接头，玻璃为竖直安装。各种材料的特性及荷载情况如下。玻璃的材料特性：fg＝72N/mm2（大面）；fg＝50.4N/mm2（边缘）；E＝72000N/mm2；v＝0.2(泊松比)；α＝0.00001。驳接头的材料特性：E＝206000N/mm2；V＝0.3(泊松比)；α＝0.000012。密封垫层的材料特性：E＝10000N/mm2。垂直于板面的荷载2KN/m2。温度差：Δt＝80℃。本算例使用Ansys有限元分析软件[13]，使用solid187的八节点单元对结构进行离散。

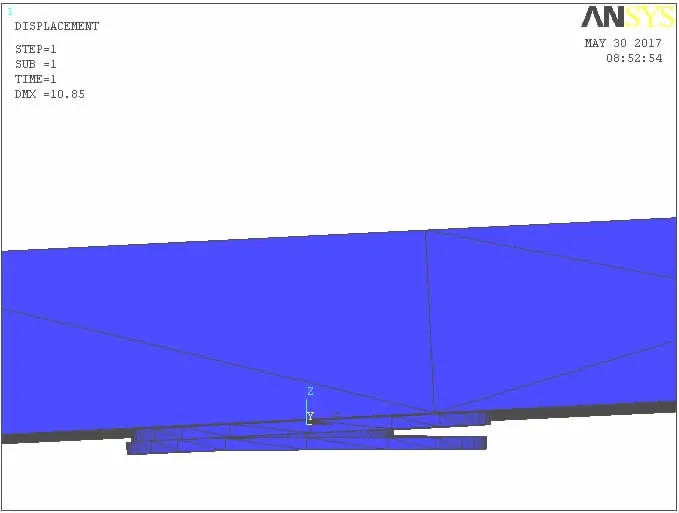
图2 采用半简化模型，在垂直于板面的荷载作用下的孔边变形示意图

为了进行对比，本文分别基于简化模型及本文提出的半简化模型进行了分析。对于简化模型，三个物体之间采用贴接（将三者实体模型建立后使用glue命令，保证三者间接触面不脱离，不滑动），接触面间整体变形。

半简化模型是典型的三维刚体—柔体接触问题。因为金属连接件的弹性模量远大于密封垫层，所以其与密封垫层的接触面称作刚性面，被当作“目标”面，程序中用Targe170来模拟3D的“目标”面；相对的，密封垫层与金属连接件的接触面称作柔性体，被当作 “接触”面，用8节点的Conta174来模拟。一个目标单元和一个接触单元叫作一个“接触对”程序通过一个共享的实常号来识别“接触对”。这一接触对属于不分开的接触，用来模拟那种一接触就再不分开的问题，这种不分开是指对法向接触而言，而面之间允许有相对滑动。同时摩擦系数定为0.4[10]。

对于竖直安装的板，其荷载状况可分三种：自重、垂直于板面和温度变化。对于自重荷载，因其主要为平行于板面的挤压应力，且数值较小，故本文中未作计算讨论。在垂直于板面的荷载下，板中应力主要是弯曲应力，其计算结果如如表1-3所示。

表1 最大应力（MPa）

表2 孔边最大位移（mm）

表3 板中心位移（mm）

从计算结果可以看出，对于孔边，因简化模型比半简化模型的变形能力小，故孔边应力相对要大，但考虑计算模型与实际情况的差异，孔边应力的计算本身只能给出一个大致的应力数值，所以用简化模型来进行计算，结果是可以接受并偏于安全的，而用半简化模型来计算较之更为准确。另外，还可以看出，采用两种模型计算得到的板中心位移，长边连线中点都是比较接近的。因此这两种计算模型对于板的挠度计算的模拟都比较准确，这一结论也符合圣维南原理。最后，在两种模型中，应力最大值出现的地方不同。在半简化模型中，垫层的VonMises应力最大值出现在垫层与玻璃板咬合的凹角，玻璃板的主应力最大值出现在孔边缘；而在简化模型中，玻璃板的主应力最大值出现垫层与玻璃板相交的边缘处，垫层应力的最大值亦出现在垫层与玻璃板相交的边缘处。

本文亦对温差工况进行了分析，简化模型下孔边应力为197.5MPa，半简化模型下孔边应力为102.3 MPa。简化模型的应力比半简化模型要大的多，这是因为简化模型中，玻璃板、密封垫层和金属连接是完全贴合的，而且没有相对滑动，所以对孔边水平方向的约束很强，使得玻璃在温度变化下热胀冷缩后产生很大的应力，而半简化模型的单元间是接触性质的，玻璃在温度变化下形变后可以脱离亦可以有水平滑动，故计算结果的应力值相对比较小。

在温度变化情况下，由于玻璃板伸缩而导致的孔边应力，其主要的性质是挤压应力，所以数值远大于垂直于板面荷载下以弯曲应力为主的情况，而玻璃抵抗挤压应力的能力是相当强的，纯压下可承受上千兆帕左右，所以不能用玻璃的抗弯应力来简单衡量。在这种情况下简化模型的计算结果是很不准确的。因为在温度变化情况下孔边的变形很复的，加上施工的原因，孔边变形能力的离散性很大，所以即便是半简化模型也不可能得到非常接近实际情况的结果，但是半简化模型可以指出温度应力的大致变化范围，因此相对而言，半简化模型的计算结果对工程实际的指导意义更强。

四、结论

本文对点支玻璃的孔边有限元模型进行了研究，首先分析了目前常用的两种模型 （简化模型和理想模型）的优缺点，在此基础上，进一步提出一种半简化模型。该模型，相比于完全简化模型，保留了金属连接件和垫层的接触关系，可以使得计算模型更接近实际情况，提高计算精度；相比于理想模型，忽略了玻璃板和垫层的接触关系，节省了计算资源，提高了计算速度。论文通过具体算例对比了简化模型和半简化模型的应用效果，结果表明半简化模型得到的结果更接近实际情况，对工程实际的指导意义更强。