一种IGBT模块的新型建模与瞬态仿真方法研究*

沈天浩，黄 瑞，杨 帆，陈俊玄，冯 权，洪文华，俞小莉*

(1.浙江大学 能源工程学院, 浙江 杭州 310000;2.上汽大众汽车有限公司, 上海 201805)

0 引 言

在电动汽车开发的前期，需要对电池、电机、电控进行选型与匹配。IGBT模块是电控的关键部件，选择合适的IGBT模块对电动汽车电控模块的设计至关重要。

IGBT在工作过程中会产生损耗导致其温度升高。IGBT模块由封装好的IGBT芯片和FWD(续流二极管)芯片组成。结温是电子设备中半导体芯片PN结的工作温度，当结温过高时会导致硅材料芯片性能降低，乃至永久损坏。据统计，由温度过高引起的IGBT失效占全部的55%以上[1]。电动汽车设计前期只能采用仿真的方法对IGBT模块进行结温预测，分析不同工况下的发热与模块结温是否符合要求。

通过仿真对IGBT模块的结温进行预测是国内外研究的重点。姚芳[2]、宋飞[3]和陈彦[4]搭建了IGBT模块的热电联合仿真模型，得到IGBT与FWD的损耗波形和结温波形，但其仅针对一维模型，未进行三维流固耦合仿真，无法得到温度场分布；陈清[5]和王淑旺[6]对某IGBT模块进行散热分析，得到其温度场和流场分布，但其仅计算稳态工况，未计算瞬态结温。

IGBT模块工作时，其芯片发热会随时间作周期性波动，芯片的结温也随之周期性变化。目前的IGBT模块仿真方法包括一维和三维仿真，但无法同时得到IGBT模块的结温分布云图和结温波动数据。

本文以型号为FS800R07A2E3的IGBT模块为例，提出一种新型IGBT模块仿真方法。

1 损耗计算

IGBT模块在运行时会产生损耗，损耗主要包括IGBT芯片和FWD芯片的损耗，是IGBT模块中的热源。

1.1 损耗计算理论

三相桥式整流电路如图1所示。

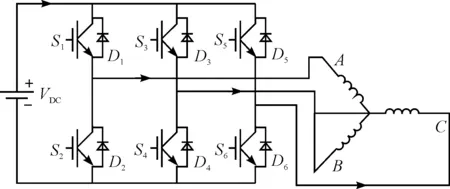
图1 三相桥式整流电路

每相包含两个IGBT芯片和两个反向并联的续流二极管(FWD)，二者工作时经历周期性的开关状态并产生损耗。

IGBT芯片的主要损耗是通态损耗[7]和开关损耗[8]，IGBT的通态损耗是由于其正向导通压降产生的，其开关损耗是因为在开通和关断的瞬间，电流和电压有重叠期；FWD芯片的主要损耗是通态损耗和关断损耗，FWD的通态损耗也是由于其正向导通电压而产生的，其开关损耗则是因为二极管的反向恢复特性。

目前，电动汽车大多采用SVPWM(空间矢量)调制方式，其损耗可以通过计算得到[9-10]。

IGBT输出特性如图2所示。

图2 IGBT输出特性

为了简化损耗的计算，IGBT的导通压降VCE与FWD的正向导通电压VF与IC的关系可以近似用直线表示：

VCE(t)=VCE0+rCE*IC(t)

(1)

VF(t)=VF0+rF*IC(t)

(2)

式中：VCE0—IGBT门槛电压；VF0—FWD门槛电压；rCE—IGBT通态等效电阻；rF—FWD通态等效电阻。

当采用传统7段SVPWM调制时，IGTB芯片和FWD芯片的损耗通过计算获得。

(1)IGBT通态损耗。

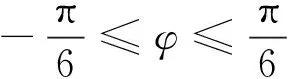
(3)

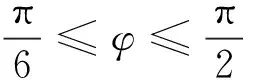
(4)

式中：IN—正弦波相电流幅值；M—调制比；φ—电流滞后电压角度。

(2)IGBT开关损耗。

(5)

式中：fsw—开关频率；Eon-nom—IGBT在标称电压Vnom和电流Inom下测得的开通损耗；Eoff-nom—IGBT在标称电压Vnom和电流Inom下测得的关断损耗；VDC—直流电压。

(3)FWD通态损耗。

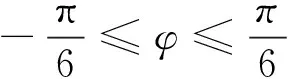
(6)

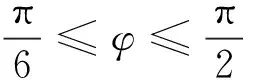
(7)

(4)FWD开关损耗。

(8)

式中：Erec-nom—FWD在标称电压Vnom和电流IF-nom下测得的反向恢复损耗。

由式(3～8)可得IGBT芯片和FWD芯片在一个相电流周期内的平均损耗，分别表示为：

PIGBT=Pcon_IGBT+Psw_IGBT

(9)

PFWD=Pcon_FWD+Psw_FWD

(10)

上式计算的是IGBT模块工作时的平均损耗。三相桥式逆变电路的基本工作方式是180°导电方式，即每个桥臂的导电角度为180°，同一相(半桥)上下两个臂交替导电，各相开始导电的角度依次相差120°。因此，一个IGBT桥臂在一个周期内只有一半时间是导通的。

IGBT芯片与FWD芯片的损耗是不规则的曲线，可以将两者的损耗函数简化为理想的半正弦波曲线。

两者瞬态损耗的函数为：

(11)

(12)

式中：PIGBT(t)—IGBT芯片瞬态损耗；PFWD(t)—FWD芯片瞬态损耗；T—相电流周期。

1.2 FS800R07A2E3模块损耗计算

1.2.1 稳态损耗

FS800R07A2E3模块中IGBT芯片和FWD芯片的特征参数分别如表1、表2所示(特征参数测试条件为300 V，550 A，125 ℃)。

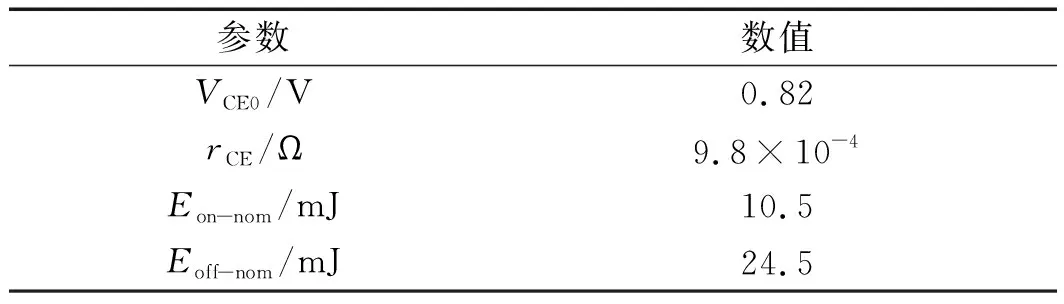
表1 FS800R07A2E3模块IGBT芯片特征参数

表2 FS800R07A2E3模块FWD芯片特征参数

IGBT模块的部分工作参数如表3所示。

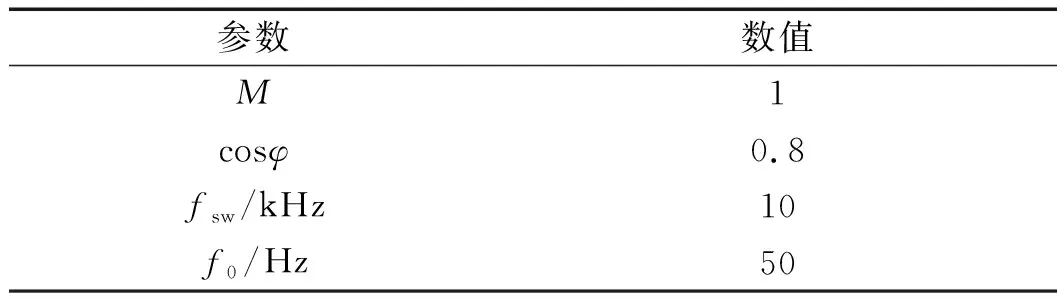
表3 FS800R07A2E3模块工作参数

注：M—调制比；φ—电流滞后角；fsw—开关频率；f0—相电流频率

不同直流电压VDC和相电流幅值IN工况下(工况1至工况3)，IGBT芯片与FWD芯片的平均损耗如表4所示。

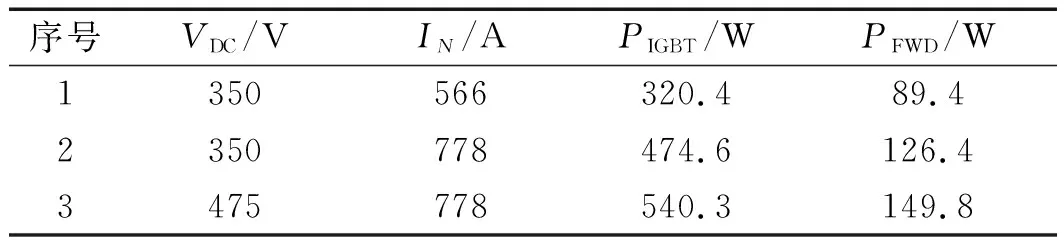
表4 不同工况下FS800R07A2E3模块的损耗

由此可见：IGBT和FWD的平均损耗均随VDC和IN的增大而增大。

1.2.2 瞬态损耗

本研究取工况1至3中发热最大的工况3计算瞬态损耗。根据一个周期内平均损耗功率相同的原理进行等效，可知等效半正弦波的幅值为平均损耗的π倍。其他工况相同时，瞬态损耗的变化周期与相电流频率有关。频率为50 Hz时，瞬态损耗拟合式为：

(13)

(14)

IGBT模块瞬态损耗曲线如图3所示。

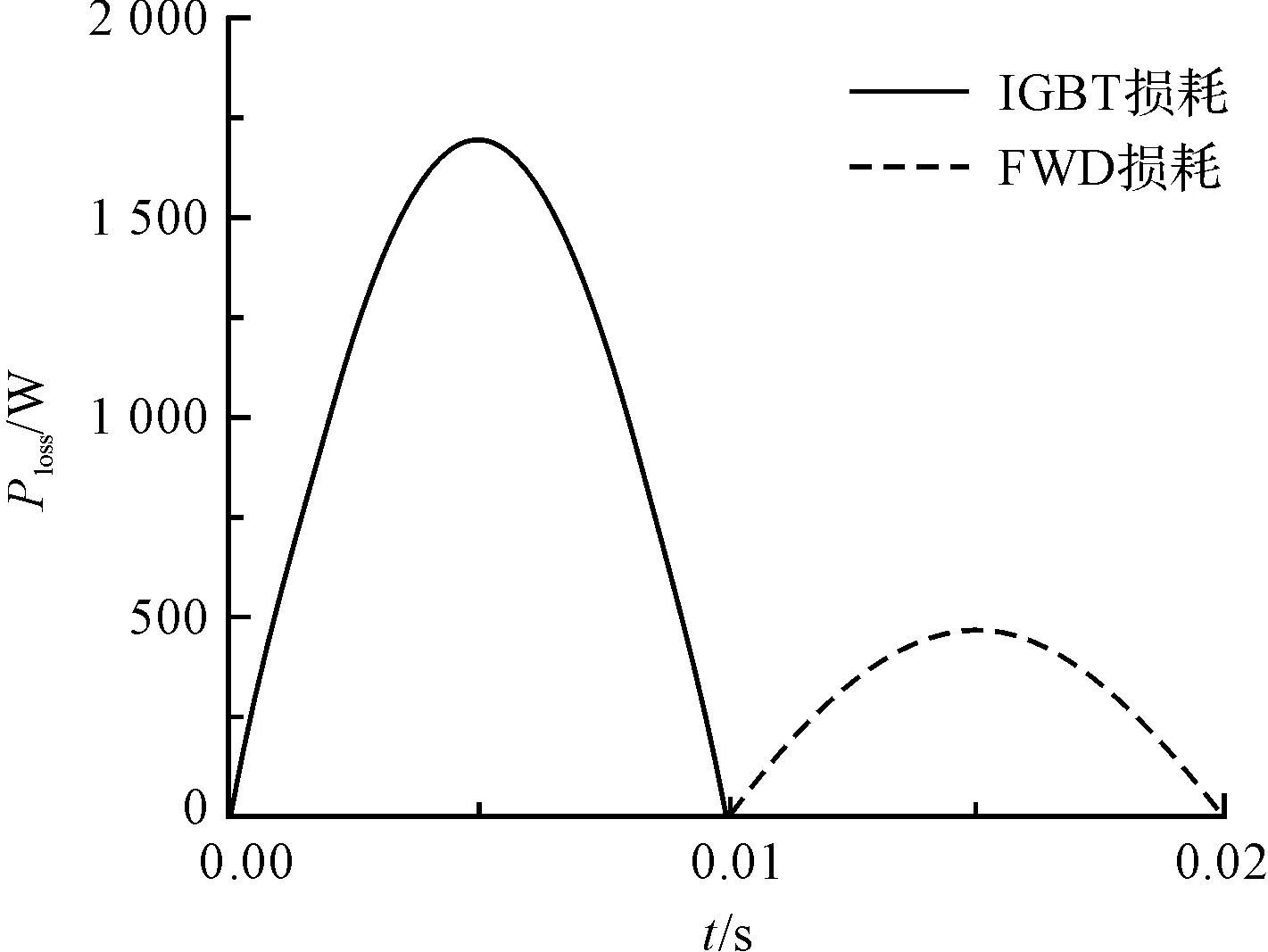
图3 IGBT模块瞬态损耗曲线

2 三维建模

在进行三维建模前，对IGBT模块的三维模型做出以下假设：(1)芯片是一个均匀发热体，芯片中所有层都是均匀的，无缺陷的；(2)芯片较薄，除了芯片截面法向外，其他表面均视为绝热；(3)忽略辐射和空气对流换热；(4)冷却液为不可压缩流体且为湍流流动。

2.1 建模与网格划分

本研究以英飞凌FS800R07A2E3模块为例，建立其三维模型。通过测量及相关资料得到模块的尺寸信息；采用SolidWorks建立模块的三维模型并进行一定的简化，去除密封圈槽，去除模块内部的连接线等对散热影响较小的结构；然后将IGBT几何模型导入到HyperMesh中进行网格划分，最小网格尺寸为0.1 mm。

三维模型和网格如图4所示。

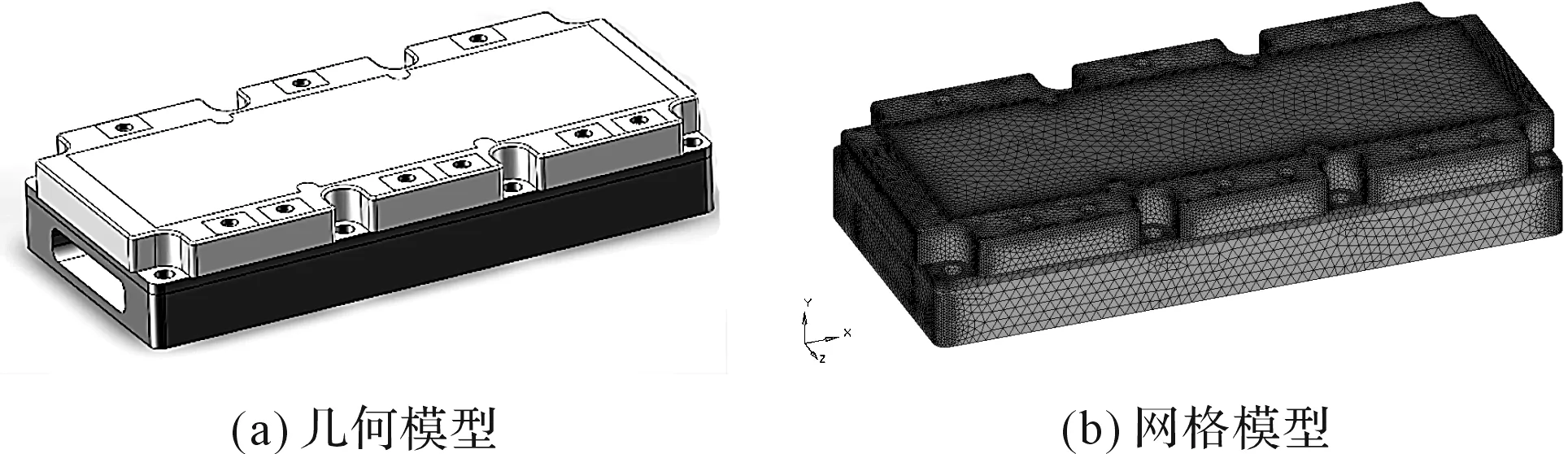
图4 英飞凌FS800R07A2E3模块模型

2.2 流固耦合计算模型

笔者采用Star-CCM+软件对IGBT模块进行瞬态三维流固耦合仿真，计算在不同工况、一定冷却条件下的结温分布和波动。

计算模型中的冷却液为不可压缩流体，满足质量守恒、动量守恒、能量守恒方程，即:

(15)

(16)

(17)

式中：ρ—流体的密度；U—速度矢量；p—流体压力；μ—流体的动力学粘度；cp—流体的比热容；λ—导热系数；F—作用在流体上的质量力；q—流体所吸收的热量；T—流体或固体温度；Φ—能量耗散函数。

冷却液在电机控制器中的流动为湍流，采用基于雷诺时均法的数值计算方法，引入湍流模型，计算中采用标准k-ε湍流模型，即：

(18)

(19)

式中：ui—U在i方向上的速度分量；k—湍动能；ε—耗散率；μt—湍流粘度；Gb—由浮生力产生的湍流动能；Gk—平均速度梯度引起的湍动能k的产生项；σk、σε—湍流普朗特数；C1ε，C2ε—经验常数。

在Star-CCM+软件中，流体域采用k-ε湍流模型，边界层设置为2层。

2.3 物性参数设置

本研究，将HyperMesh中的面网格导入到Star-CCM+后，设置相应材料的物性参数。物性参数设置的对象包括内部芯片、外壳材料、导热基板、冷却液等，物性参数包括材料的密度、导热系数、比热容等。由于IGBT芯片的多层结构，网格密度无法细小至此，笔者采用复合导热系数的计算方法对其进行折算[11]。

芯片材料为硅，基板材料为铜，外壳材料为工程塑料，冷却液为50%水与50%乙二醇的混合物。

2.4 边界条件设置

FS800R07A2E3模块为三相全桥整流，每个全桥由两个半桥组成，一个半桥由4个IGBT芯片和4个FWD芯片组成。半桥内部的实际结构和简化三维模型如图5所示。

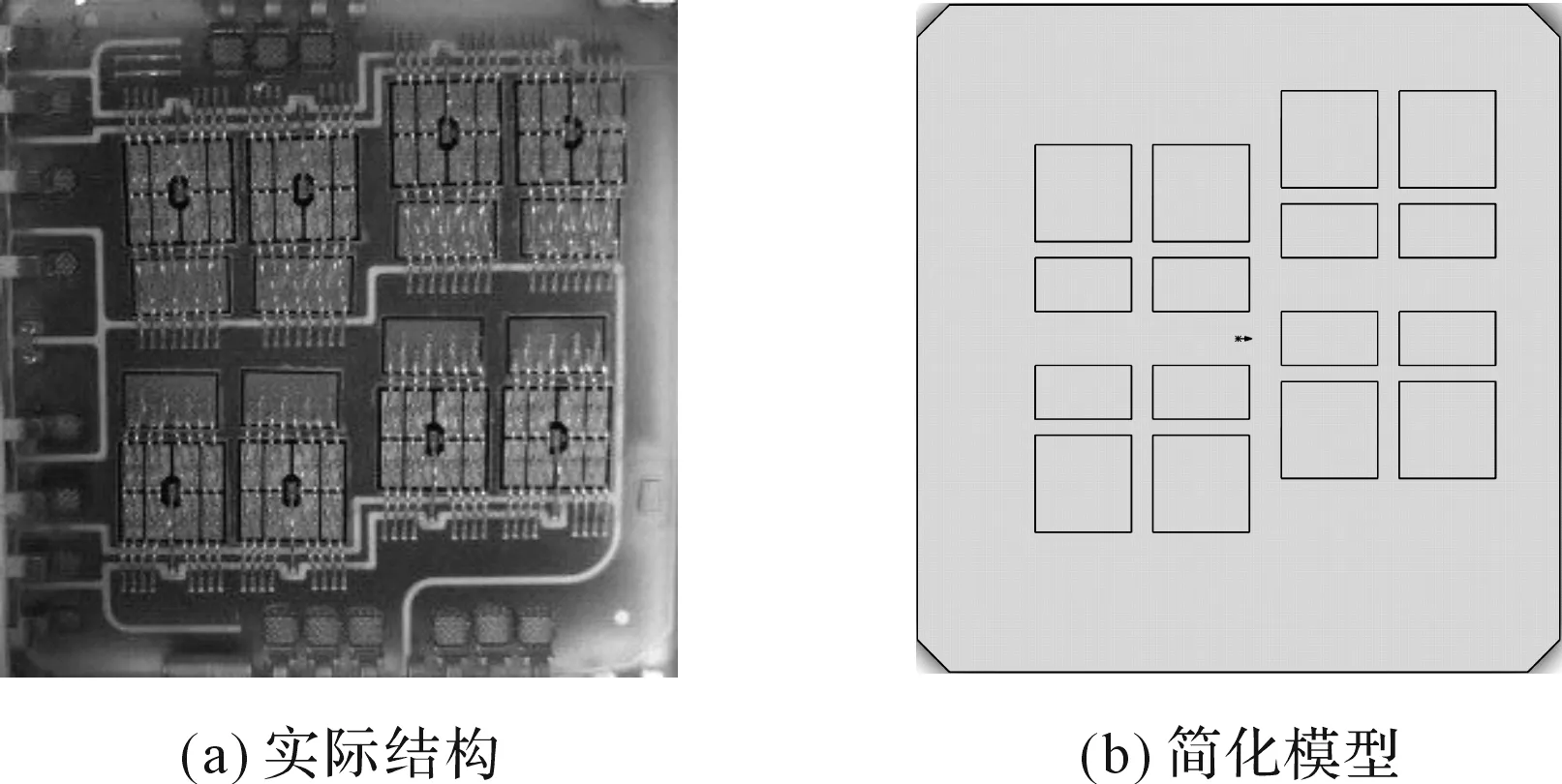
图5 英飞凌FS800R07A2E3模块半桥

本研究将上述IGBT和FWD芯片的发热模型作为边界条件，加载至三维模型，稳态加载为常数，瞬态加载为时间的函数。

电机控制器的入口温度一般要控制在65 ℃以下，本文计算最恶劣工况，即冷却液入口温度为65 ℃，流量为10 L/min。

3 仿真结果

3.1 稳态仿真结果

本研究将上述稳态工况的发热功率设定为边界条件，对其进行仿真。在迭代500步以后仿真收敛，得到IGBT模块的温度分布云图。流固耦合计算得到的温度分布如图6所示。

图6 稳态仿真温度分布云图

图6中，左侧为冷却液入口，右侧为出口。定义冷却液入口到出口分别为U/V/W相，U/V/W三相的最高温度存在温差，稳态下最高温度出现在W相的IGBT芯片，最高结温约为122 ℃。

各相芯片的最高温度如表5所示。

表5 各相芯片最高温度

三相温度的不均匀性在2 ℃左右，分析其原因可能为U相靠近冷却液入口，冷却液温度较低，因而带走热量较多。

3.2 实验结果及分析

通过查阅数据表可以获得不同冷却液流速下的热阻，结合冷却液温度和散热功率，可以计算模块的最高结温。仿真数据与实验数据对比如表6所示。

表6 三维仿真模型验证

表6中，本文三维仿真模型得到的稳态仿真结果与厂家实验数据之间的误差在2%以内，验证了三维模型的正确性。

3.3 瞬态仿真结果

在稳态计算中，W相远离冷却液入口，温度最高，本文仅计算W相最高结温波动。将上述瞬态损耗公式加载至W相，U相和V相的损耗仍采用稳态损耗加载。瞬态时间步设置为0.001 s，每个时间步包含50步迭代步数。由于从冷起动开始计算需要消耗大量计算资源和时间，因此将初始条件设置为稳态计算的结果。

由于瞬态热源的周期性波动，W相IGBT芯片和FWD芯片的温度也周期性波动。瞬态结温波动数据如图7所示。

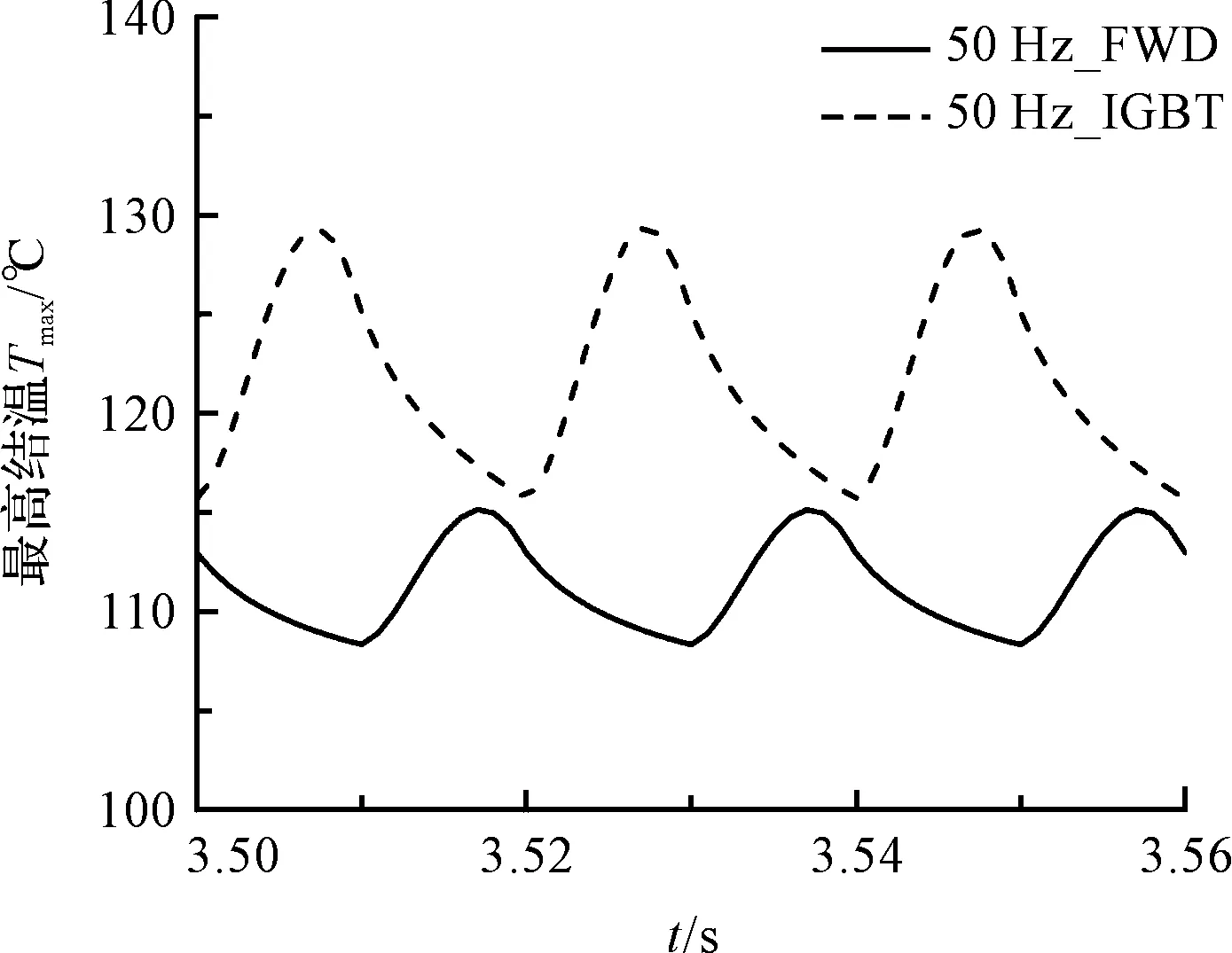
图7 W相芯片结温波动

图7中，相电流频率为50 Hz时，热源的周期为0.02 s，结温波动的周期也为0.02 s。在前三分之一周期内IGBT芯片温度上升，后三分之二周期内温度下降，最高结温大约出现在周期的三分之一处。IGBT芯片的最高结温达到129 ℃左右。

由于同一相中IGBT芯片温度高于FWD芯片，本研究考察不同频率下IGBT芯片的结温波动。不同相电流频率下IGBT芯片结温变化如图8所示。

图8 不同相电流频率下结温波动

图8中，相电流频率越高，最高结温越低。可以解释为：在芯片发热的一个周期内，前部分周期芯片发热，冷却液带走的热量比发热少，导致结温升高；后部分周期内芯片不发热，冷却液持续带走热量，导致结温降低。

4 结束语

本文以英飞凌FS800R07A2E3模块为例，提出了一种新型的IGBT模块的仿真方法,得到以下结论：

(1)IGBT模块内部三相芯片的最高结温存在2℃左右温差，一维瞬态计算无法模拟三相间温差与温度分布云图；

(2)IGBT模块进行选型时，仅采用稳态仿真是不够的，其结温波动需要通过瞬态仿真得到；

(3)IGBT的实际结温存在周期性波动，并且与相电流的频率相关。在电机控制器设计阶段，可以考虑采用提高频率的方法以降低IGBT模块的最高结温；

(4)采用瞬态仿真和流固耦合结合的方法，既能仿真得到结温分布云图，也可以获得结温波动数据。