基于过程模态的薄壁件铣削稳定性实验研究*

田卫军，任军学*，李 郁，王大振，张宝刚

(1.西北工业大学 现代设计与集成制造技术教育部重点实验室，陕西 西安 710072；2.西北工业大学 明德学院,陕西 西安 710124)

0 引 言

由于具有质量轻和高强度的特点，近年来薄壁结构件在航空、航天工业得到了广泛应用。但是由于结构刚性弱等缺点，因此在加工过程中极易出现振动现象，造成加工表面质量恶化、变形、噪声、影响加工效率等问题。因而薄壁件的数控加工已经成为机械加工中的一大难题，很多学者和工艺人员都开展了这方面的技术研究。

早期，通常在粗、精加工之间安排一次或数次半精加工，一次或数次时效处理工序，通过消除切削、夹紧过程产生的应力和零件本身的残余应力，使变形发生在最后精加工之前。REN[1]在发动机叶盘高效粗加工过程中，采用工序分散、时效处理、多次修复的方法减小应力引起的变形问题，并在工艺刚度增强方面采用胶粘、浇灌等方法来增强零件刚性和紧固零件，如浇灌石腊、浇灌石膏、应用低熔合金等，结果表明，通过该方法可以有效抑制颤振，保证叶片加工精度和表面质量；随着有限元技术的发展，部分学者开始采用有限元分析与实验结合的方法，通过改善夹具装夹位置达到改善抑制振动和减小变形的目的；PAN[2]利用有限元方法建立了接触力模型和接触变形模型；随着研究的深入，部分学者开始尝试从切削力优化与加工误差补偿及刀位轨迹规划方面提出了变形和颤振抑制解决措施；LIU[3]通过建立刀具的动力学模型，在考虑工件/刀具系统的变形和工件的回弹变形条件下，获得零件连续稳定切削加工中任意点的加工误差；QU[4]以切削力的回归模型作为目标函数，提出了一种确定切削用量和最大加工效率的最佳加工参数组合的优化方法；在刀位轨迹优化方面，基于几何误差模型的数学表达式，FU[5]提出了五轴机床精度优化补偿方法；ZHANG[6]提出并开发了一种基于在机测量的叶片精密加工误差自适应补偿方法；在高速加工方面，通过修正的Johnson Cook模型，TANG[7]建立了高速铣削薄壁件限元模型，并对薄壁零件变形区的切削力、切屑形态、有效应力、有效应变和切削温度进行了模拟，为薄壁铣削变形控制提供了一种补偿途径；WAN[8]采用Visual C++软件计算了钛合金在高速铣削精加工过程中的颤振稳定域，找到加工参数的最佳组合，从而获得了最大无颤振材料去除率。

上述的振动变形问题并未考虑薄壁件加工过程中自身结构模态特性的变化对振动的影响，因此本文将通过分析铣削过程薄壁件模态演变规律，结合铣削动力学模型的振幅响应曲线，对铣削过程的工艺参数转速进行优化，并通过实验以验证该方法的可靠性，为后期薄壁件的切削提供参考。

1 铣削动力学模型参数优化

铣削动力学模型是表征加工过程稳定性和加工误差的基础，合理建立铣削模型对于铣削参数优化至关重要。

1.1 铣削动力学模型

就薄壁件铣削而言，可以假设工件为柔性件，刀具为刚性件的“刚性刀具—柔性工件”工艺系统，如图1所示。

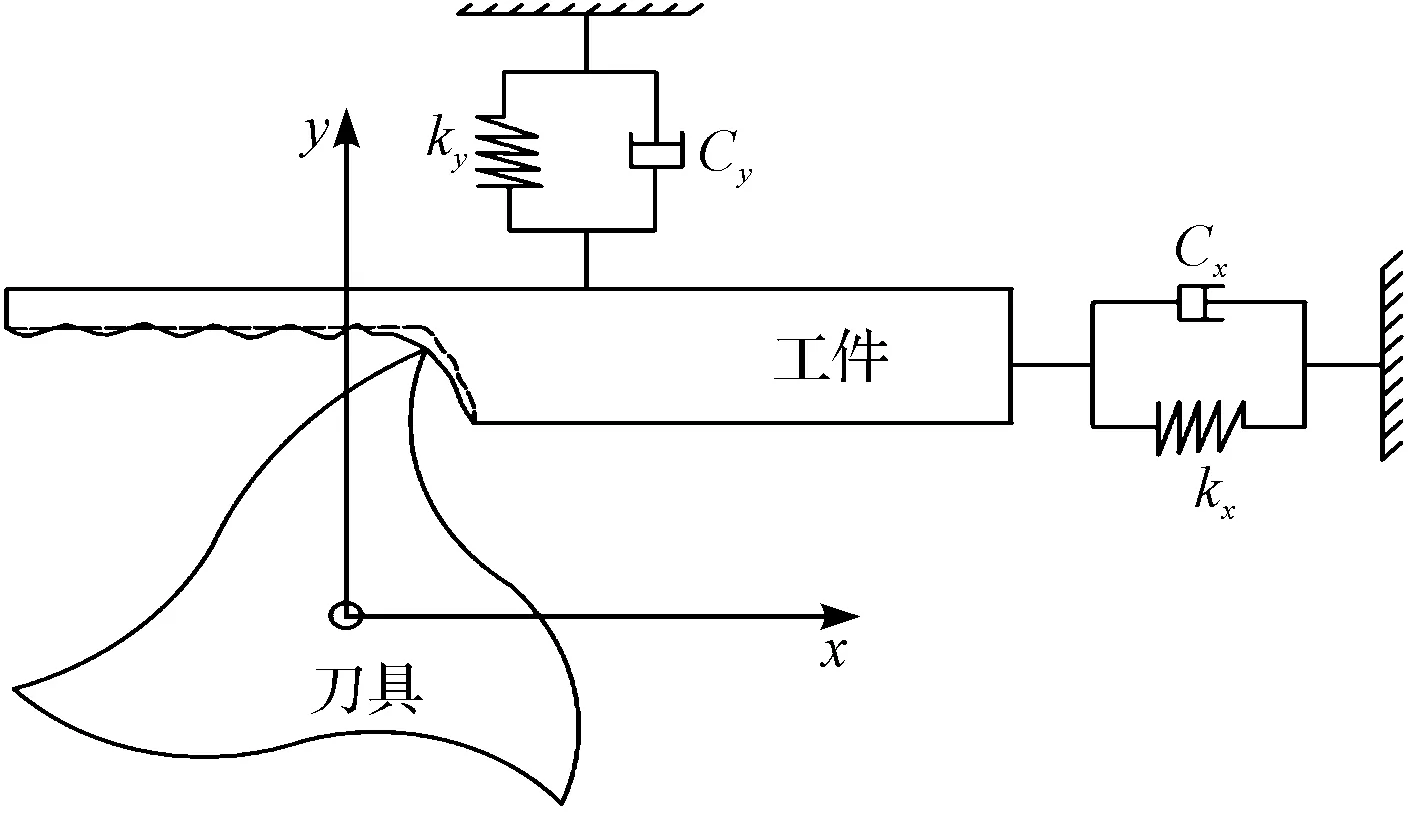
图1 刚性刀具—柔性工件工艺系统

对于上述的铣削动力学模型，可以采用动力学微分方程进行描述[9]:

(1)

式中：r—位移矢量；M，K，C—系统质量、刚度和阻尼矩阵，它们表述了铣削工艺系统自身的结构特性，与机床构型、操作设备以及结构件有关。

式(1)的右边所表示的是系统外部的激励，即切削力，静态力Fs、过程阻尼力Fed、动态切削力。如果将激励全部分解在x、y两个方向，y方向为主受迫振动系统，x方向的次受迫振动，则振动系统动力学方程可以表述为：

(2)

针对薄壁件而言，x方向的次受迫振动实际计算可忽略不计，同时对于金属材料，在实际切削加工时，阻尼矩阵[C]受工件材料和结构影响较大。因此，薄壁件阻尼矩阵可以考虑采用刚度与质量矩阵组合的瑞利阻尼方法求解[10]，则有：

C=αM+βK

(3)

此时的阻尼比为：

(4)

式中：α，β—瑞利阻尼常数。

通过模态实验可以确定任意状态两相邻固有频率ω1、ω2和阻尼比ξ1、ξ2，将其代入式(3，4)中，联立求解可得：

(5)

(6)

再将得出的α、β代入式(4)中，即可得到任意第i阶的阻尼比ξi与固有频率ωi的关系。由此可知，方程左侧结构系数通过模态实验可完全确定。

1.2 振动响应振幅

在通过实验方法获得方程两端系数的条件下，对动力学方程进行求解，则工件的响应振幅可以表达为：

(7)

进一步将式(4)代入到式(7)中，即可得到振幅响应关于频率的函数关系式为：

(8)

此时，通过切削转速与频率关系：

ωi=ni×z/60(ni—转速，r/min；Z—刀具齿数)，将其代入(8)式中,就可以得到不同激励转速下薄壁件振幅大小。

振幅响应可以表述为：在不同的激励频率下，由薄壁件材料的去除过程结构参数(M、K、C)改变对振幅的影响程度；其次，通过模态实验获得不同加工阶段薄壁件结构的振幅函数表达式，即可通过绘制振幅函数曲线指导主轴转速域选择。

2 模态测试实验

模态测试实际就是利用实验测量的激励信号(力锤激励信号)和响应的时间历程信号，通过数字信号处理技术获得频率响应函数(FRF)，从而获得系统的非参数模型的过程。

2.1 模态测试方法

测量系统由加速度传感器、力锤和动态采集仪及模态分析软件组成。力锤及加速度传感器通过信号线与动态采集仪相连。所测信号通过电缆与电脑完成数据通讯，工作原理如图2所示。

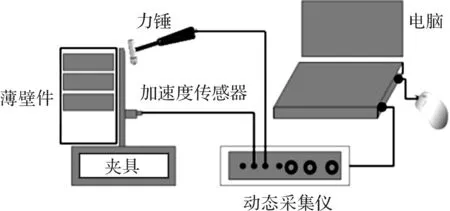
图2 模态测试原理图

实际模态测试时采用的仪器设备如下：

力锤采用Dytron2302-1型，其灵敏度为1.02 mV/lbf；加速度传感器丹麦B&K，灵敏度为10.73 mV/G；动态采集仪采用亿恒AVANTMI-7008测试系统。

实际测试工件及现场如图3所示。

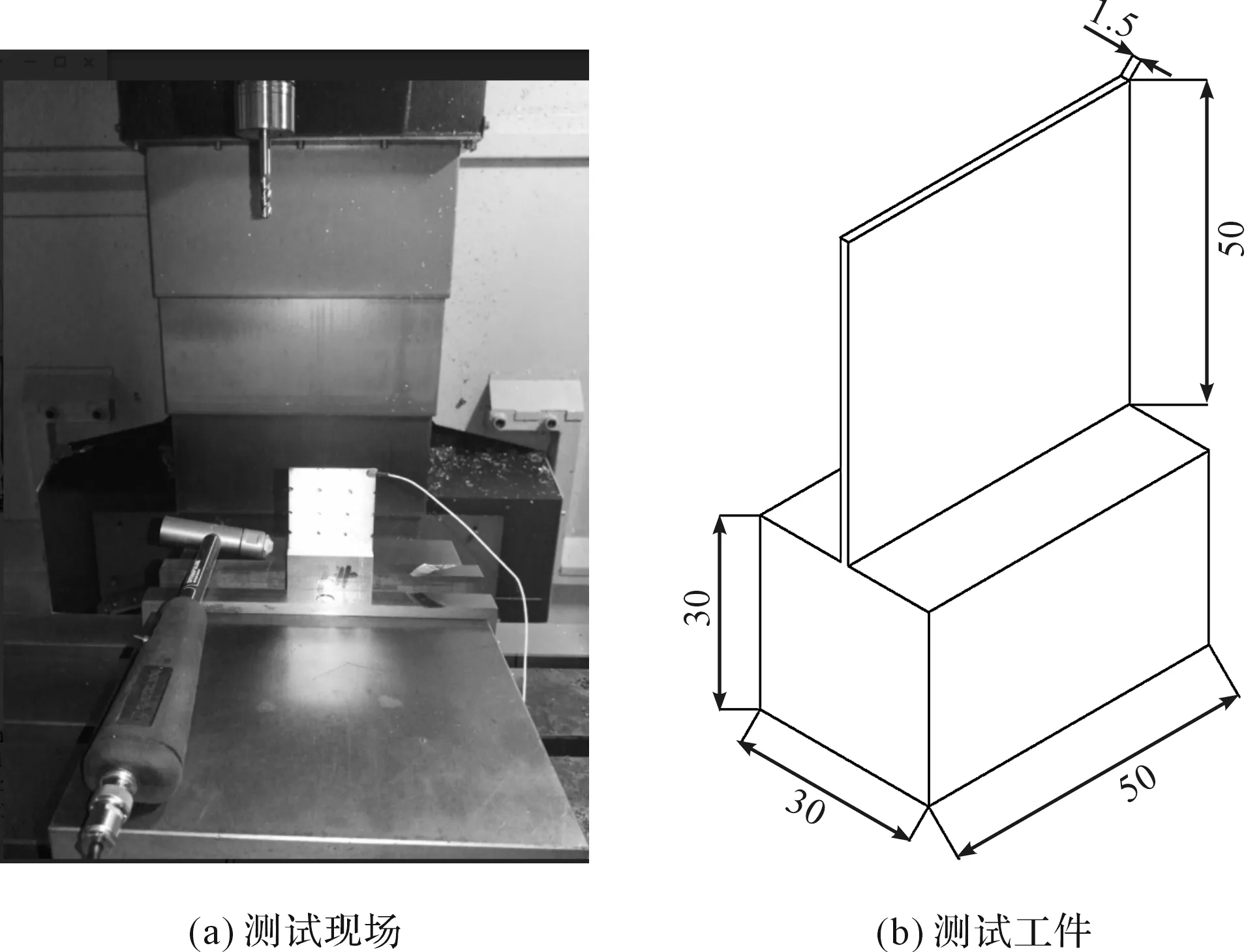
图3 测试工件及测试现场

2.2 铣削实验条件

为了得到薄壁件铣削时的振动规律和模态显著演变过程，测试工件的材料选用钛合金TC4，薄壁件部分结构尺寸50×1.5×50 mm，刀具选用Φ10 mm，齿数8齿球头铣刀，机床选用友佳VM850立式加工中心，平口钳装夹方式。

同时，为了保证薄壁件铣削的稳定性和防止单边铣削变形问题，铣削方式采用了对称螺旋铣削方式，切削深度3 mm，切削宽度0.25 mm，加工完后壁厚1 mm，采用乳化液冷却方式；分别对切削深度为0 mm、8 mm、16 mm、24 mm、32 mm状态进行间歇性测试和模态数据采集。

2.3 实验测试结果

为了结合实际测试过程，分析薄壁件在铣削过程中模态的演变规律，本文分别提取了铣削前后0 mm、8 mm、16 mm、24 mm、32 mm这5种状态下的频率和振型，如图4所示。

图4 不同铣削状态下频响函数曲线

通过观察图4频响函数曲线可以发现：

(1)随着材料切削去除过程的进行，虽然切削深度的增加引起薄壁结构在发生变化，但是图形上的振型几乎不发生变化，一阶频率表现出“一弯”，二阶频率“二扭”，三阶频率出现“二弯”，四阶频率出现“二扭”和有限元分析结果一致；

(2)随着切削深度的加大，零件的壁厚进一步变薄，动态刚度曲线整体有所下降。

最后，通过频响函数可以提取到不同状态下前四阶实测固有频率，如表1所示。

表1 不同铣削状态下固有频率

3 实验结果分析

3.1 模态测试结果分析

不同铣削深度下薄壁件的前四阶固有频率如图5所示。

由图5可以看出：材料去除对模态频率有较大的影响，尤其对高阶四阶固有频率的影响很大，整体是下降的趋势。原因分析如下：

频率的变化实际上就是由于薄壁件结构的质量和

图5 不同铣削工艺过程频率变化

刚度变化引起。随着铣削的进行，材料不断被去除，薄壁件模态刚度和模态质量都会呈现出整体下降趋势，但是模态刚度和模态质量这两个因素谁的变化占主导地位谁就决定了模态频率的变化趋势。当模态刚度下降占优时，模态频率下降较快；而模态质量下降占优时，模态频率又有上升趋势。该结论可以从图5说明：在加工的初期(0 mm～16 mm)和末期(24 mm～32 mm)模态质量下降的变化影响局部占优，此时频率曲线较缓上升；随着加工的进行，在中间部位时，模态刚度变化在整个过程中整体占优，因此频率呈现明显的下降趋势，整个固有频率范围内，尤其是三、四阶频率变化最为显著。

从图5的演变规律还可以看出：在实际生产中，如果要整个工件的铣削过程避免共振，以提高生产效率为目标时。在机床设备允许的前提下，可以采用图5虚线②附近或更高的恒转速切削频率进行加工，这个转速段上下都远离共振区。除此以外，可以考虑采用变转速切削的方法，即在加工的初始阶段采用一种转速，到薄壁件中间部位时，可以提高转速；最后根部阶段可以进一步提升，从而保证工件有效远离共振频率。

通过上述分析，以频率演变曲线做为前期最佳转速的一种初选。在避免共振的条件下，通过演变规律曲线可以得到的最佳转速域范围为：[0-2 000 r/min]、[3 000-6 000 r/min]、[7 000-8 500 r/min]、[>10 000 r/min]。

3.2 振幅响应曲线分析

通过式(8)可以绘制得到4种不同铣削状态下的振幅响应曲线，如图6所示。

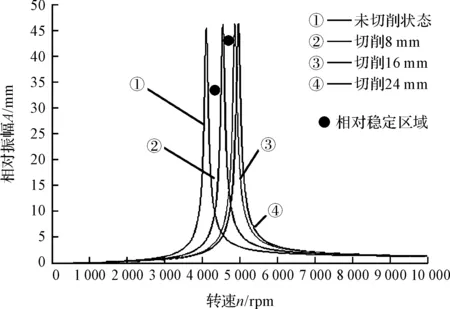
图6 不同转速下的振幅响应曲线

图6中的响应曲线进一步表述了不同转速下的振幅响应大小，其为最佳转速的进一步优化提供了参考依据。

在考虑加工效率和实际机床自身特性条件下，依据模态频率演变规律预选转速的[0～2 000 r/min]和[>10 000 r/min]可以去除。针对剩余两个预选区域[3 000 r/min～6 000 r/min]、[7 500 r/min-8 500 r/min]。首先分析[7 500 r/min-8 500 r/min]区域范围，在7 000 r/min和8 500 r/min时，对应的激励频率分别为933.3 Hz和1 133.33 Hz。

结合表1中的各状态固有频率可知：在7 000 r/min激励频率，其相对远离切削4种状态时的四级共振频率，是一个绝对稳定区域；而8 500 r/min时激励频率比较接近切深在24 mm、32 mm时的2阶共振频率。因此，综合比较而言，若采用恒转速时，7 000 r/min比较可靠；若要采用8 500 r/min，在切深加大时则需要考虑变速问题。同理分析[3 000 r/min-6 000 r/min]区域时，从共振曲线可以看出：3 000 r/min激励频率为400 Hz，结合表1可知，其远离各切削状态下的共振频率，是一个绝对稳定转速。而当[3 000 r/min～6 000 r/min]该范围内时，从图6曲线可以看出：整体幅值密集偏高，故稳定性相对要差，选择不当很容易发生共振，若要在该区域选择转速，从共振响应曲线可以看出：4 200 r/min和4 800 r/min附近相对比较稳定，共振振幅相对较小，但仍会出现振动。进一步结合表1各状态分析，4 200 r/min和4 800 r/min激励频率为560 Hz和640 Hz。4 200 r/min激励频率非常接近初始切削时的固有频率，所以很容易产生共振造成切削初始就出现振动。而4 800 r/min激励频率产生的激励频率接近后续的切削中的1阶频率，所以在后续切削的4种状态下，需要考虑采用变速才可以满足需求。

综上所示，若针对该薄壁件铣削过程如果采用恒定转速，在机床允许转速范围内，可以考虑3 000 r/min附近和7 000 r/min两种最佳转速；如果兼顾效率，可以采用变转速方案考虑4 800 r/min→7 000 r/min。

3.3 切削表面形貌分析

通过铣削实验得到不同转速下铣削表面形貌，如图7所示。

图7 不同转速铣削表面形貌

从图7可以看出：转速为3 000 r/min时和7 000 r/min切削质量相对最好，振纹很小，切削过程稳定。在转速为4 800 r/min是切削质量次之，且当切削深度大于8 mm时，有振动出现。当转速为4 200 r/min时加工质量最差，切削过程在初始状态时就有明显振动。实际切削结果与理论分析一致。

为了验证方法的可靠性，本文将所提出的方法用于某航空发动机叶片的实际工程化验证，如图8所示。

图8 工程化验证

利用实验获得了模态，本文再结合振幅响应曲线进行参数优选，最后采用恒定转速和变转速的两种方案，结果显示，所得到的工件加工质量明显优于以前。

4 结束语

通过对薄壁件的铣削过程分析，本文建立了薄壁件铣削振幅响应与结构参数的关系，并提出了一种最佳主轴参数的选择方法，具体如下：

(1)通过模态实验分析不同工序状态下模态演变规律，提取了各状态下的固有频率，并揭示了铣削过程中模态刚度和模态质量谁的变化占优势地位决定了模态频率的变化趋势，该规律为避开加工共振区域提供了参数预选的理论依据；

(2)在预选参数的基础上，通过振幅响应曲线可以进一步优化主轴选择范围，为实际加工提供稳定切削参数；

(3)在薄壁件的数控铣削中，时变的模态参数对于稳定性的预测影响至关重要；在保证切削稳定性的条件下，本文提出了恒转速切削和变转速的切削方案，方案得到了工程化验证。