纯电动汽车车身稳定控制器多目标优化研究*

陈启鹏，李志华，彭 伟

(杭州电子科技大学 机械工程学院，浙江 杭州 310018)

0 引 言

目前，国内外针对电动汽车稳定性问题的研究主要分为3个方向：

(1)对制动力分配进行改进。CHEN[1]提出了一种防抱死制动过程中再生制动系统的新型控制算法，并验证了该策略能够改善车辆在不同紧急驾驶条件下的稳定性和制动性能；WANG[2]基于最优预测控制设计方法并且和李亚普诺夫理论相结合,提出了一种新的制动力分配策略，该策略提高了再生制动效率以及制动稳定性；李玉芳[3]对制动力分配曲线进行了多目标优化,并且建模仿真验证了其优化后分配方法能提高制动力回收效率；KHALED[4]对于制动力分配曲线进行了研究，结果表明了ECER13法规曲线的安全意义；张凤娇等[5]对再生制动力进行了多目标优化，使再生制动效率和车身稳定性得到了提升；OLEKSOWICZ[6]研究了防抱死制动系统和再生制动之间的关系；KIM[7]用遗传算法获得了再生制动最优转矩分配，得到了最佳的前后轮制动力矩；于卓平[8]对四轮轮毂电机进行了制动力分配优化，优化后汽车稳定性得到了较大提升。

(2)通过车身稳定控制器进行制动力控制，获得更好的车身稳定性。张金柱[9]设计了基于滑模理论的车身稳定性控制器，纠正汽车行驶状态；HAH[10]在前驱混合动力汽车上提出了基于成本函数控制器，结果表明：该控制器提高了制动能量回收性能；LIANG[11]提出了在一种高效的能量恢复控制策略基础上修改后的非线性模型预测控制方法，并且验证了其安全及高效性；WANG[12]描述了一些模拟环境如严重的转弯情况，通过软件仿真，验证了自适应方法的有效性，并与传统的控制器进行了比较。

(3)通过提高汽车信号输入精度来增大车身稳定性。LU[13]研究了四轮驱动电动汽车对于行驶路面附着系数估算方法；HAN[14]通过新的自适应方法来实时估计车辆侧滑角；NAM[15]通过增加轮胎侧向传感器来精确估计电动汽车侧滑角，提高了车身横向稳定性。

尽管国内外对制动系统开展了一些研究，但大多数都在单独领域进行研究，制动力控制器不仅关系到转向稳定性而且对制动能量回收也有影响。车身稳定控制器分配制动力需要结合路面、汽车速度、汽车转角、车身质心侧偏角等数据。

本文将对制动力系统进行模块化设计，即通过车身稳定控制器控制增加电机制动力,并选择对该制动力进行多目标优化。

1 整车动力学模型

1.1 二自由度车辆模型

为了方便建立车身动力学方程，本文忽略汽车转向系统，以及悬架系统，车身只做平面前后直线运动和绕z轴转动,两个自由度。二自由度车辆模型如图1所示。

图1 二自由度车辆模型

其运动方程为：

(1)

(2)

式中：m—汽车质量；Cf，Cr—前后车轴的侧偏刚度；δ—前轮转角；Iz—汽车的转动惯量；lf、lr—汽车前后轴至质心的距离；vx—纵向速度；vy—侧向速度；ω—横摆角速度；β—质心侧偏角。

1.2 车辆稳定性分析

车辆行驶状态由车辆行驶速度、转角以及车身横摆角速度决定。汽车的横摆角由横摆角速度决定，质心侧偏角与横摆角之和为车辆实际转向角度。

车辆运行的转向特性可分为3种：车辆正常转向、车辆转向角度不足以及车辆转向角度过度。当车辆转向正常时，车辆的实际转角角度与方向盘的输入角一致，此时汽车按照驾驶员预期路径行驶；当车辆实际转向角与方向输入角不一致时，可能会出现转向不足或转向过度，严重时甚至翻车。

为提高车辆稳定性，笔者使用车身稳定性控制器来控制电机制动力。根据方向盘转角δ和车速vx，由二自由度车辆模型确定理想质心侧偏角βdes和理想横摆角速度ωdes。以质心侧偏角偏差(β-βdes)和横摆角速度差(ω-ωdes)作为目标函数，通过增加电机制动力使得质心侧偏角偏差、横摆角速度差最小，使车身能够按照期望路径行驶。

1.3 理想质心侧偏角、横摆角速度

根据地面附着系数、汽车行驶速度以及汽车转向输入角可以得到理想质心侧偏角以及理想横摆角速度：

(3)

(4)

式中：ωdes—理想横摆角速度；βdes—理想质心侧偏角；L—车身总长度。

则质心侧偏角偏差和横摆角速度差状态空间形式如下：

(5)

2 能量再生制动系统

电动汽车制动时，制动力由液压制动系统与电机再生制动系统同时提供。汽车总的制动力为：

Fb=αFhyd-max+λFmot-max

(6)

式中：Fb—制动力；Fhyd-max—液压制动系统提供的最大制动力；Fmot-max—电机可以提供的最大制动力；α—液压制动力系数(0≤α≤1)；λ—电机制动力系数(0≤λ≤1)。

当电机提供的制动力大于制动所需要的制动力，此时液压系统不工作，α=0；当制动所需要的制动力大于电机所能提供的制动力时，此时电机提供制动力为最大制动力，λ=1。α的值由汽车完成制动过程所需要的制动力以及电机最大提供的制动力所决定。制动总功率Pb由电机的再生制动功率Pe与液压系统制动功率Pf提供，则有：

Pb=Pe+Pf

(7)

将上式对时间求积分，制动过程所需要的能量为:

(8)

在制动过程中，理论情况下可回收最大能量为:

(9)

在不考虑风阻以及其他能量损失的情况下，根据能量守恒定律有:

(10)

液压制动Ef又可以由下式得到:

(11)

故可以将ΔE改写成：

(12)

能够有效回收的能量为：

Pr=K1·K2·K3·Pe

(13)

式中：K1，K2，K3—机械传动效率、发电机发电效率和储能装置的充电效率；Pe—电机的能量再生制动功率。

储能装置的充电电流为：

(14)

式中：U—储能装置端电压；Te—电机再生制动转矩；Ω—电机转速。

3 电源系统仿真

3.1 锂电池工作原理

锂电池能量密度大、循环性能优越、输出功率大，适合作为纯电动汽车车载能源使用。本文使用的电池模型为PNGV模型，如图2所示。

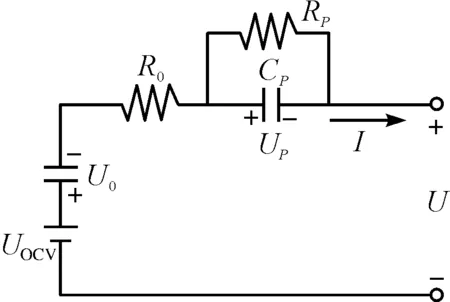
图2 PNGV模型

该模型精度高，是在原有模型的基础上增加一个电容用于表征开路电压随电流积分变化，被广泛应用于电动汽车研究中。

根据电路KVL定律，该模型方程为：

U=UOCV-U0-UP-IR0

(15)

式中：U—端口电压；UOVC—开路电压；R0，RP—电池内阻和极化内阻；CP—极化电；I—电路电流。

3.2 发电机工作状态

制动能量回收系统如图3所示。

图3 制动能量再生系统

汽车处于制动过程时，电机处于发电状态。直流发电机的电流方程为：

Uout=Ce·nd·Φd-IdzRa-U0

(16)

式中：Ce—反电动势常数；nd—电机转速；Φd—电机主磁通量；Ra—电枢电阻；U0—电池的电压；Uout，Idz—电枢电压和电流。

4 电—液联合制动系统及优化目标

4.1 制动力分配方式

电—液联合制动系统在不改变制动安全性前提下，多让电机制动系统参与制动过程。电—液联合制动制动策略如图4所示。

图4 电—液联合制动制动策略

当驾驶员根据路况踩下制动踏板，此时位移传感器采集到踏板的角度及角速度信号，计算出当前状况下所需要的制动力，根据所需要的制动力判断驾驶员的制动意图选用不同的制动方式，同时根据路况进行制动力分配。当制动模式判定为轻度制动时，电机单独提供制动力，此时制动力都能用于能量回收；当制动模式判定为中度制动时，电机所能提供的扭矩小于汽车制动所需要的扭矩，此时电机优先参与制动，制动力不足的部分由液压制动系统提供，此时电机制动提供的制动力可以用于能量回收，液压制动提供的制动力不能用于能量回收；当紧急刹车时，为保证汽车及驾驶员的安全，仅有液压制动参与制动。

4.2 制动回收系统影响因子

由锂电池的充电特性可知,当电池SOC值过高时,应该停止电机参与制动，表达式为：

(17)

电机在低速情况下制动回收效率低,甚至回收的能量不够用于自身功率损失，此时应该仅采用机械制动，表达式为：

(18)

4.3 车身稳定控制器

车身稳定控制器用来提高车身的稳定性能。控制器如图5所示。

图5 车身稳定控制器

控制器分为两个部分：第一部分控制器根据方向盘转角输入、汽车行驶速度和汽车二自由度，计算理想质心侧偏角和理想横摆角速度。当ωdes与ω、βdes与β相等时，则第二部分控制器不参与制动，制动力分配系统按照理想制动力分配曲线分配前后制动力；当ωdes与ω、βdes与β不相等时，需要在理想制动力分配基础上通过第二部分控制器对4个车轮增加电机制动力，使得汽车的ω与ωdes、β与βdes接近，从而让汽车转向角度接近方向盘输入角。

4.4 优化目标

通过车身稳定控制器控制电机制动力使得横摆角速度和侧偏角接近理想状态，以保证汽车行驶安全性。优化目标一为：

(19)

为保证制动回收效率最高，选择优化目标二为：

(20)

式中：Y2—制动能量回收优化目标;I，U—纯电动汽车电源电压和充电电流。

4.5 设计变量及取值其范围

4.6 优化设计约束

4.6.1 电机扭矩特性

本文采用永磁同步电机作为汽车动动力装置,当汽车制动方式为电机制动时，电机处于发电状态。根据电机的转矩特性可知：当电机转速低于额定转速时,电机以恒转矩运行；当电机转速高于额定转速时,电机的转矩随转速的增加而减小。电机的最大再生制动力为：

(21)

式中：Tmax—电机能够提供的最大转矩;Tn—电机额定扭矩；Ω—电机的转速；Pn—电机的额定功率;Nn—电机额定转速。

4.6.2ECE制动法规约束

汽车制动过程中,前后轴制动力分配应当满足ECE R13法规，即制动强度z在0.15≤z≤0.8范围时,前轴利用附着系数曲线应该要大于后轴利用附着系数；z≤0.15时没有限制,此时仅仅通过电机提供制动力。

4.6.3 制动舒适性约束

由于液压制动的介入速度低于电机制动的介入速度,联合制动和两种单独制动在制动舒适性上会有差异。20世纪90年代,实验人员建立了制动感觉指数试验评估体系，制动感觉评估体系可以有效反应制动舒适性。本文制动力突变约束为:

(22)

式中：α—制动感觉极限线性指数系数，本文选为0.7。

4.7 多目标优化遗传算法

多目标遗传算法就是在多个目标函数之间，尽可能找出使各目标函数达到最优解集。遗传算法不受问题的限制，收敛性、鲁棒性优越,能够有效地保持种群多样性以及均匀性。带精英策略的非支配排序遗传算法(NSGA-Ⅱ)是最近较前沿的优化方法。NSGA-Ⅱ算法计算过程如图6所示。

图6 NSGA-Ⅱ算法

优化过程中，笔者首先建立目标Matlab模型，然后使用Isight软件进行优化。设计变量在优化空间中进行基于NSGA-Ⅱ优化算法的自动搜索及迭代运算，实现车身稳定控制器再生制动力矩的优化。优化过程中设置种群规模为80,交叉率0.8，变异率为0.06。经过多次迭代运算，得到一系列Pareto解集汽车参数，如表1所示。

表1 电动汽车参数选择

目标函数最终收敛，得到Pareto最优解，个体分布性较好，得到分布均匀的Pareto前沿，优化结果令人满意。质心侧偏角随时间变化曲线如图7所示。

图7 质心侧偏角变化曲线

横摆角速度随时间变化曲线如图8所示。

图8 横摆角速度变化曲线

仿真建模时用到的优化结果如表2所示。

表2 优化结果

5 建模仿真及结果分析

本文搭建了基于Carsim动力学仿真软件与Matlab/Simlink软件的虚拟仿真平台。仿真结果如下：

汽车在附着系数为0.4的路面上，汽车行驶仿真结果中，质心侧偏角如图9所示。

图9 质心侧偏角曲线

横摆角速度变化曲线如图10所示。

图10 横摆角速度变化曲线

由图分析可知：在连续转弯的情况下，汽车质心侧偏角控制在安全的范围内，稳定性能很好。分析图9行驶过程中车身横摆角变化平滑，没有出现上下抖动等状况，这表明优化后的电机力矩提高了汽车的操控稳定性。

本文在第2个仿真路况选择为ECE城市道路运转工况模型。汽车SOC值随时间变化曲线如图11所示。

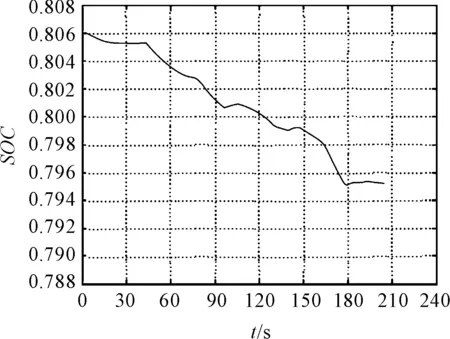
图11 SOC值变化曲线

不同优化方法对比结果如表3所示。

表3 不同优化方法对比结果

在减速工况中，电池的SOC值均有上升，减速结束后加速行驶，电池的SOC值又随之下降。从表3中可以看出：本文优化后的制动系统在制动回收和车身稳定性方面都有不错的提升；对比滑模变控制法和成本函数控制法可知：汽车经稳定器控制后汽车在转弯时质心侧偏角小，车身横摆角速度低，安全性能更加优越，制动能量回收效率高。

6 结束语

本文提出了基于车身稳定控制器控制的制动力优化设计，对该制动力进行了多目标优化，分析了制动过程中的约束条件，采用非支配排序遗传算法进行了优化，并利用Carsim与Matlab/Simlink软件联合仿真，构建了电动车仿真平台。

理论分析和仿真结果都表明：优化后的制动力能够很好地控制车身的稳定性，车身转向能够符合驾驶员期望，实际横摆角速度和质心侧偏角能很好地跟踪期望值；对比滑模变控制法和成本函数控制法，汽车在转弯时车身更加稳定，安全性能更加优越，制动能量回收效率也有提升。