滚筒输送线路径规划方法研究*
2018-08-03薛志强游有鹏
薛志强,游有鹏
(南京航空航天大学 机电学院,江苏 南京 210016)
0 引 言
滚筒输送线是由电动滚筒、光电传感器、控制器、条码识别模块等设备组成的一种传输系统,由于其具有可定制化、空间利用率高、成本低等优势,被广泛用于物品分拣、生产线连接和物流系统集成等场合[1]。
目前,滚筒输送线的部件已逐渐标准化,从而形成了更高集成度的滚筒输送机,包括直线两方向传送输送机、圆弧两方向传送输送机、直角四方向移载输送机、两方向升降输送机和斜坡输送机等功能模块。升降输送机和斜坡输送机使得输送线可能存在三维多层结构;而直角移载输送机模块拥有4个方向的传输移载功能,是输送线中的重要节点模块,使输送线更加柔性化。
随着现代物流系统的发展,需求更加复杂化、多样化,滚筒输送线系统面临较多的挑战。一条输送线中各个输送机之间构成复杂的拓扑关系,需要特殊的数据结构来描述。在复杂输送线结构中,从某入口到某出口可能会出现多条路径,不同路径根据传送距离、传送时间和一定的约束等存在优劣之分。如何选择最优的可行输送路径,是本文要解决的路径规划问题。目前,国内外关于输送线路径规划方法的研究,主要基于网格法划分的环境模型,运算量较大、实时性较差[2]。
本文将以滚筒输送线为对象,构建其环境模型并进行优化,充分考虑输送线系统中的实际影响因素,引入路径规划算法,解决滚筒输送线中的路径选择问题。
1 输送线结构环境模型
1.1 输送线结构建模
滚筒输送线的模块之间需建立连接关系,才能形成完整且流通的输送线,完成相应的功能。这里采用有向图的数据结构来构建输送线复杂连接,用邻接矩阵为图结构的储存方式。
假定输送线有n个模块,构成图G=(V,E)的n个顶点,即V={v0,v1,...,vn-1},图的邻接矩阵是一个n×n的二位数组,用A[n][n]表示,且数组的元素为:
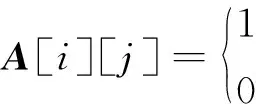
(1)
式中:A[i][j]=1—模块i和模块j之间有连接,且连接方向为从模块i指向模块j;A[i][j]=0—模块i和模块j无任何方向的连接。
上述无加权的有向图能准确描述滚筒输送线的结构,便于上位机图形绘制、动态监控等,也易于实现较少模块输送线的路径规划。但对于模块数量较大、连接较复杂的输送线,基于上述图结构模型进行路径规划变得较为困难,需要对上述建模方法进行适当改进。
1.2 滚筒输送线结构模型改进
针对滚筒输送线的特点与路径规划需求,可以对上述图结构模型进行适当的简化与改进。事实上,滚筒输送线中只有移载输送机模块可以完成3个或4个方向的路径选择;作为入口或出口的输送机模块是整个输送线的结构边界;而其他模块只具有传输功能,相互连接路径唯一,不存在路径选择。
根据上述特点,本文将以入口、出口、3个或4个方向的移载输送机作为节点,节点之间的其他输送机连接作为加权路径,对输送线图结构进行简化。
在重新构建的输送线图结构中,节点与节点之间可能存在多种不同类型输送机连接组合,进而形成一条路段通道,路段长度计算方法成为首要解决的问题。
本文采用输送机当量来衡量路径长度,计算方法如下:
(2)
式中:Qij─从i节点到j节点路段上的输送机当量;m─输送机类型总数;k(1,2,3…,m)─输送机类型标号;qk─该路径上第k类输送机的数量;fk─第k类输送机的当量换算系数。
各类输送机当量换算系数如表1所示。

表1 各类输送机当量换算系数
本研究以直线传送输送机为参考基准进行取值,具体可根据实际情况进行调整。
输送机当量换算系数取值方法:在相同条件下,多次测试、计算并统计物品通过各类输送机所用时间与通过直线传送输送机所用时间的比值,以各类输送机对应的比值数据的平均值为其相应的当量换算系数。
某一较复杂输送线结构简化后的例图如图1所示。
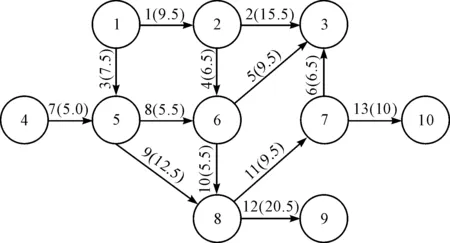
图1 输送线结构简化例图
近100个输送机模块的输送线,简化后仅有10个节点。该图结构中节点集合为{①,②,③,④,⑤,⑥,⑦,⑧,⑨,⑩},路段集合为{1,2,3,4,5,6,7,8,9,10,11,12,13},箭头所指为节点间路段上的物品传送方向。节点①、④为入口节点,节点③、⑨、⑩为出口节点,其他节点都为移载模块节点,从而构成6组路径规划需求。图1中,各个路段号后括号内的数字为对应路段的输送机当量。
如从节点⑧到节点⑨的路段12中,输送机当量为20.5,其计算方法如下:假设路段12包含15个直线传送输送机、2个直角移载输送机、1个180度圆弧传送输送机、1个升降输送机,则依据式(2)得其输送机当量为:15×1+2×0.5+1×1.5+1×3=20.5。
按照上述方法对复杂输送线的结构模型改进后,再建立有向图结构,邻接矩阵中的值为各个路段的输送机当量,节点自身的输送机当量为0,节点之间无直接连接的输送机当量为无穷大。
采用这种改进的结构模型可简化图结构和路径规划的难度,因此下文路径选择优化算法的设计将以此为基础。
2 输送线的路径规划
2.1 基于Dijkstra算法路径选择优化设计
输送线的功能是将物品从特定的入口送入,经过一定的路径送达特定的出口。为了提高输送能力,需要获取从特定入口到特定出口的最短路径。
Dijkstra算法是求解单源最短路径规划的经典算法[3-4],将其用于输送线的最短路径规划的流程如图2所示。

图2 迪杰斯特拉算法求解输送线最短路径流程图
以图1为例,假定需计算从入口①到出口⑩的最短路径,首先建立图结构邻接矩阵所对应的二维数组Edge[10][10]。
为求解最短路径及长度,需要设置并计算3个一维数组:数组dist[10]表示当前从节点①到其他节点的最短路径长度(初始值为Edge中的第一行);数组source[10]表示当前节点是否已被检测(0为未检测,1位已检测,初始时候只有节点①对应的值为1,其他都为0);数组path[10]表示从节点①到某节点的最短路径上该节点的前一个节点序号,最后可以采用倒向追踪法来确定最短路径上的各个节点[5-6]。
对于规模较小的图结构,应用Dijkstra算法求解输送线的最短路径较方便;而当简化后的图结构仍然比较复杂时,启发式智能算法则具有更好的实时性和鲁棒性。
2.2 基于蚁群算法的路径选择优化设计
蚁群算法是依据蚂蚁种群总是能找从巢穴到食物之间的最短路径而提出的一种启发式算法,不仅与输送线的最短路径模型类似,而且具有良好的实时性,便于实现动态路径规划。
蚁群算法中路径选择含有贪心规则的不利因素,引入选择概率来避免完全贪心规则而陷入局部最优,而启发函数对路径选择概率有较大的影响。通常,传统蚁群算法采用距离启发函数ηij(t)=1/dij,这种启发函数容易使得蚂蚁贪图当前的一小步,进而选择偏离目标方向的节点。依据输送线图结构的节点松散、路径静态等特点,对启发函数进行改进,增加目标节点对选择下一节点的影响,改进后的启发函数如下:
(3)
式中:dij─节点i到节点j的路段长度;djg─节点j到目标节点g之间的路段长度。
将式(3)引入到蚁群算法中,得到蚂蚁k在t时刻由节点i转移到节点j的概率,如下式所示:
(4)
式中:τij(t)—t时刻在路段(i,j)上的信息量(初始状态下各路径上的信息量都相等,为常数);α—信息素启发因子(衡量信息量对是否选择该路径的影响程度);β—期望启发因子(衡量启发信息对蚂蚁选择路径的影响程度);allowedk—蚂蚁k可选择节点的集合[7]。
当所有的蚂蚁在输送线图结构上完成一次路径选择后,需要对各路径上的信息素进行更新,即:
τij(t+n)=(1-ρ)·τij(t)+Δτij
(5)
(6)
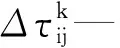
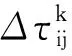
(7)
式中:Q—信息素加强系数;Lk—第k只蚂蚁在本次迭代中所走过的路径长度[8-9]。
根据输送线图结构的实际情况,本研究对蚁群算法中的参数进行取值,值的选择因模型而异,需要不断调整找到平衡点,进而求出最优路径。
采用蚁群算法求解输送线最短加权路径及长度流程图,如图3所示。
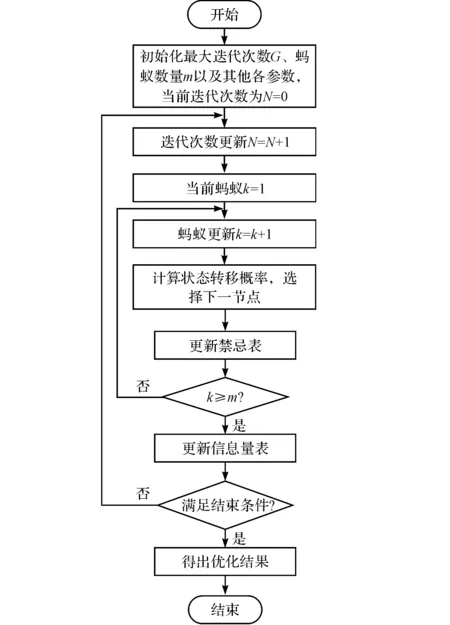
图3 蚁群算法求解输送线最优路径流程图
禁忌表用于记录当前已知的不可能在最优路径上的节点,信息量表用于记录各个节点的信息素。
需要注意的是,尽管蚁群算法比Dijkstra算法更适合于规模较大的路径规划,且具有良好的实时性和鲁棒性,但参数选择不当仍能会影响求解。
2.3 实际工况约束下的输送线路径规划策略
在装配生产线等输送线系统中,某些工况需要对最短路径进行修正,主要归纳为以下两类:
(1)某个物品必须经过输送线中的某个节点进行特殊处理;
(2)当前最短路径上某个路段通行压力较大。
针对第一类情况,如果路径必须包含某节点N,对2.1和2.2中的算法修正策略如下:先求解从起点到节点N的最短路径及长度,再求解从节点N到终点的最短路径及长度,最后进行拼接组合即可。该处理策略可以扩展应用于必须包含多个节点的路径规划问题。
针对第二类情况,如果当前搜索到的最短路径上的路段P(i,j)较为拥堵,对2.1和2.2中的算法修正策略如下:可以根据拥堵的情况,通过适当的权数来增加路段P(i,j)的路段长度(Dijkstra算法中增加Edge[i][j]的值;蚁群算法增加dij的值)。这种处理策略可以增加选择其他较通畅路径的概率,进而达到最短路径修正的目的[10-11]。
具体应用中,两算法的选择还需结合输送线规模和算法的具体特点:规模较小的输送线采用Dijkstra算法,规模较大的输送线优先用蚁群算法;去蚁群算法无法求得最优路径的情况下,再用Dijkstra算法重新求解。
2.4 实例分析
本研究以图1所示系统为例,采用Dijkstra算法和蚁群算法分别求解图1中从入口节点①到出口节点⑩的最优路径,再加入2.3小节中两种约束,对路径重新规划,分别得出最优结果,如表2所示(Dijkstra简写为Dij)。
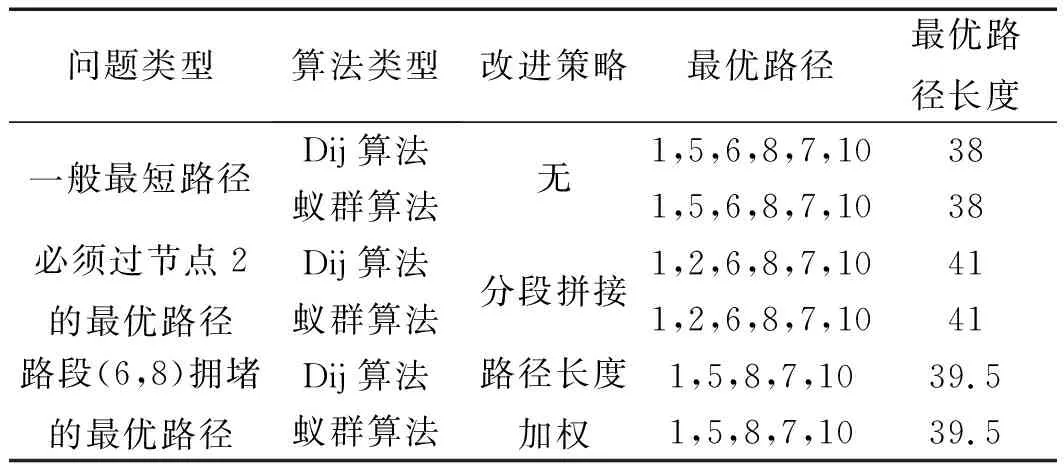
表2 输送线最优路径规划算法结果验证
由表2可知:两种算法的求解具有相同的结果,且为实际最优路径。
3 结束语
本文分析了滚筒输送线的环境模型,提出了以输送机当量衡量路径长度的计算方法,并对较复杂输送线的结构模型进行了改进。
研究的结果表明:
(1)改进后的结构模型简化了图结构,并降低了路径规划的难度;
(2)针对最短路径选择问题,分别采用较为经典的Dijkstra算法和启发式的改进蚁群算法进行求解,分析了两种算法的适用场合;
(3)针对输送线应用的两种实际工况,提出了相应的动态修正策略,为解决这两类约束下滚筒输送线路径最优规划提供了有效的解决方案,也可为其他类型输送线的路径规划提供借鉴。
