强化数学思想方法，倡导课堂深度教学

2018-08-02广东王常斌

教学考试(高考数学) 2018年3期

广东王常斌

数学是思维的体操，数学学习的目的是使人变得聪明，让学习者学会解决问题的一般方法和步骤.而长期以来，我们教学走入一个误区，重知识的传授而忽视了对学生能力的培养或者说忽视了对学生智力的开发，表现出来的现象或者是满堂灌，或者是题海战术，新课的讲解缺少知识的发生发展过程，就像章建跃老师说的“一个定义，三项注意，几个例题，大量练习”，这样的教学培养的学生对知识理解不到位，知其然而不知其所以然，更达不到“何由以知其所以然”.只会死搬硬套，只会死做题，做死题，碰到真正灵活，需要有较多的思维参与的题，也难以考出高分.2016年新修订的考纲中明确提出了从数学思想方法、数学能力、数学的科学与人文价值三个方面考查学生的数学学习情况，这体现了知识与能力并重、科学与人文兼顾的精神，同时也是对我们教学的一种导向.

在一次高三地市级组织的模拟考试中，某区的数学平均分与其他几个区相比有优势，但一本上线人数却并没有领先，甚至还落后于有些区.仔细分析得分情况，可以发现该区学生在基础题方面做得相对较好，但在“难题”方面得分率很低，出现这种现象的原因是多方面的，经过笔者的了解，其中一个很重要的原因在于教师在教学中缺少对学生数学思想方法上的训练，教学缺乏深度，致使学生的能力达不到要求.因此我们应加强数学思想方法的教学，提倡深度教学、智慧课堂，以提升学生的数学素养.下面举例进行说明.

一、分类讨论思想

【例1】(理7)五个人围坐在一张圆桌旁，每个人面前放着完全相同的硬币，所有人同时翻转自己的硬币.若硬币正面朝上,则这个人站起来;若硬币正面朝下,则这个人继续坐着.那么,没有相邻的两个人站起来的概率为

( )

教学启示：本题是一模理数第7题，文数第7题为姊妹题，只是将题中的五个人改成了四个人而已.此题文科得分率37%，理科得分率36%，考虑到是选择题，故学生实际掌握此题的应该不超过20%.为何得分率这么低？主要是分类讨论思想掌握不好，不知道将“没有相邻的两个人站起来”分成3种情况来处理.因此，我们在评讲此题时要告诉学生解题时要从思想方法的角度去思考.

分类讨论思想是一种重要的数学思想方法，在高中阶段很多时候会用到，如解双绝对值不等式的问题，含参数的函数求单调区间问题等，它在高中阶段的每个知识版块中均会涉及.分类讨论思想一定要弄清楚两个问题：一是在什么情况下要分类讨论；二是分类讨论的标准是什么.另外分类时要做到不重不漏，教学中一定要适时渗透分类讨论思想，不能就题讲题.

二、函数与方程思想

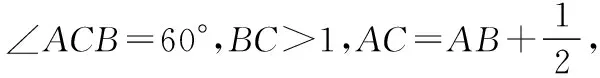
试题分析：本题考查正弦定理、余弦定理的应用，考查利用均值不等式或判别式法求最值，考查函数与方程思想.基本思路：

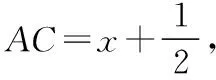
设△ABC的周长为m，根据题意可得

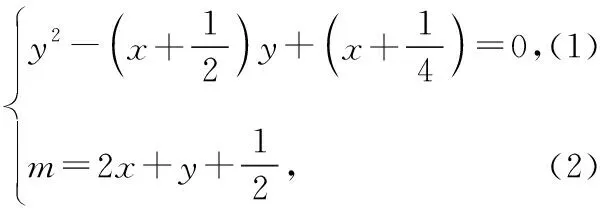
共有三个未知数，按常规思路，必须列出三个方程才能解出未知数的值，但我们只能列出两个，故还需要一个条件才能求出未知数的值.细读题目，我们发现还有一个条件未用，即“△ABC的周长最短”，这个条件就可以考虑用函数求最值的方法来处理，由此我们有以下两种思路：

思路1：因为(1)式中x为一次项，故很容易用y表示出x，然后代入(2)式，通过基本不等式或导数求函数m的最值，从而求出y的值.

思路2：因为(1)式是关于y的一元二次方程，故可用判别式法来求值域.

6y2-2(n+2)y+(2n+1)=0， (3)

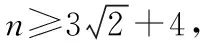
本次考试中文数17题，考查数列，其中第一问也用到了函数与方程的思想.在教学中我们应加强函数与方程思想的教学，利用函数与方程的思想来指导我们解决相关问题.

三、转化与化归思想

【例3】(文理10)《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑．若三棱锥P-ABC为鳖臑,PA⊥平面ABC,PA=AB=2，AC=4,三棱锥P-ABC的四个顶点都在球O的球面上,则球O的表面积为

( )

A.8π B.12π C.20π D.24π

试题分析：本题文理同题，均为第10题，它考查对立体几何中基本图形——阳马、鳖臑的识别，球的表面积计算，考查学生对割补法的掌握，考查学生的作图能力、运算求解能力以及转化的数学思想.解题的基本思路如下：

思路1：直接找出球心为PC的中点O，从而求出球的半径，进而计算球的表面积.

思路2：将鳖臑补形成长方体，长方体的外接球就是鳖臑的外接球.

教学启示：此题也是在考题中渗透中国古代数学文化的一种体现.上学期高二文数是填空题，此题平均分0.62，得分率为0.124，即只有约1/8的学生能做对，本次一模为选择题，理科的得分率为44%，文科的得分率为38%，排除一些误打误撞的，本题真正掌握和理解的学生也就在1/3左右.上面的两种思路中，思路1直接找出外接球的球心对多数学生是较难的，但如果我们在平时的教学中能对课本中的内容(本题图来自必修2课本69页的探究题)适当的做一些补充与拓展，学生明白阳马和鳖臑是由长方体分割而来的，就马上会想到利用思路2将此题求鳖臑的外接球表面积转化为求长方体的外接球表面积，学生还会觉得难吗？思路2就采用了转化的数学思想，将不熟悉的问题转化为熟悉的问题来解决.转化的数学思想在我们的学习中司空见惯，因此我们一定要强化转化与化归的数学思想，灵活地运用转化与化归的数学思想会给我们带来许多意想不到的收获.如下例：

【例4】(理19)如图1，在直角梯形ABCD中，AD//BC，AB⊥BC，BD⊥DC,点E是BC边的中点,将△ABD沿BD折起，使平面ABD⊥平面BCD，连接AE,AC,DE,得到如图2所示的几何体.

(Ⅰ)求证：AB⊥平面ADC；

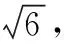
本题为此次模考的理科第19题，学生的得分率较低，特别是第二问全区得分率才10.4%，难点有几个：一是不会根据题目条件求线段AB的长；二是不会合理建系；三是建系后不会求某些点的坐标.如有些同学按如图3所示进行了建系却写不出点A的坐标.实质上还是学生对立体几何基本图形缺乏认识，我们看三棱锥A-BCD的四个面均为直角三角形，它就是一个鳖臑！只是它的摆放不符合我们的视觉习惯而已！根据第一问可知，图中本来就有三条两两互相垂直的线段：AB,AD和DC，只是它们没有交于同一点，如果我们将此图形进行适当的旋转变换，让平面ABD水平放置，如图4，建系就很容易了.因此最合理的建系，是下面的图5，这样建系是最易写出坐标的，计算也相对容易.

可见，转化的数学思想有多么重要，我们在教学中一定要反复强调，经常训练，要让学生善于联想，将陌生的问题与我们学过的、见过的内容联系起来，经过适当的变换，将新问题转化为旧问题来解决.

四、数形结合思想

( )

试题分析：本题考查三角函数的图象与性质及定积分的应用，考查运算求解能力、推理论证能力及数形结合思想.解题思路：

根据题意可画出如下草图.

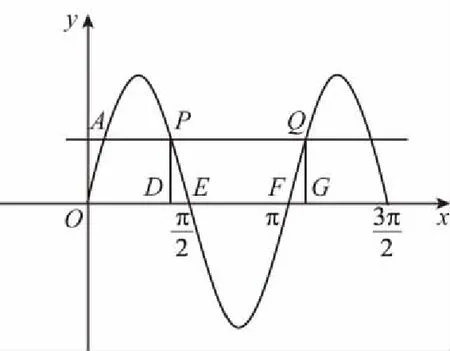
思路3：用估算法，如图，根据正弦函数的对称性，可将所求的面积转化为图中阴影部分的面积，显然它大于矩形LMNK的面积，而SLMNK=|MN|·|LM|=π，故所求的面积应大于π，而选项中B,C,D均小于π，故选A.

教学启示：本题学生的得分率为29.5%，得分率如此之低，一是有些考生不能正确画出图形；二是sin2x的原函数求错；三是大多数同学是按思路1来做的，一部分列式会出错，而且运算较复杂，即使列式正确，运算也可能出错，所以此题若利用思路2来求，列式和计算都会简单很多.课本上虽然没有直接给出思路2中的计算公式，但我们在教学过程中要引导学生推导出此公式，并利用此公式来求曲边梯形的面积.思路3利用数形结合思想可很快得出答案，体现了小题小做的解题灵活性，但也有个缺点，假如此题换成填空题，或者有两个或两个以上选项大于π，则此法失灵，故思路3有一定的局限性.所以综合来看，我们觉得思路2是一定要掌握的.此题无论采用哪种思路来解题，正确画出图形是基础，所以此题考查了数形结合思想，特别是思路3，将数形结合思想体现的淋漓尽致.