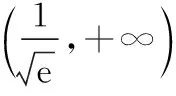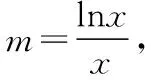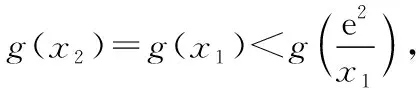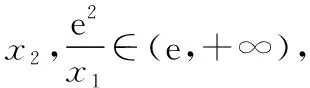层峦叠嶂巧攀援 深思熟虑多联系
——对全国卷Ⅰ函数与导数压轴题的解法研究
2018-08-02浙江杨育池
浙江 杨育池
《考试大纲说明》明确提出了高考“考查基础知识的同时,注重考查能力”,强调“重点内容重点考”.由于导数是初等数学与高等数学联系的一个纽带,具有揭示函数性质的强大功能,为处理函数与不等式问题提供新思路和新途径,能体现其应用价值和思维价值,因而,“函数与导数”问题成为历年各省份高考数学试题中的重点考查知识和“压轴戏”,其综合性强,解法灵活多变,对数学成绩影响很大.
因为导数考查形式多变我们就毫无方法了吗?显然不是这样.年年岁岁考期同,岁岁年年考题异.教师们应有准备地研究其命题规律和解题策略.2016年开始,大部分省市高考开始回归全国卷,分析对比这两年的高考试题中的导数问题,对高三复习极具参考价值,可以发现试题的考查“画风”由知识型向能力型转变,活跃于函数的单调性、极值等问题,其中不时闪现不等式的身影,已由简单考查“如何求导数”转向深入考查“如何应用导数”——利用导数研究函数的单调性、函数的零点、利用极(最)值证明函数不等式成了命题热点.
例题(2016·全国卷Ⅰ理·21)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.
(Ⅰ)求a的取值范围;
(Ⅱ)设x1,x2是f(x)的两个零点,证明:x1+x2<2.
一、层峦叠嶂忧何宜,借取月色巧攀援
纵观近两年的“函数与导数”压轴题,本题具有典型性,它在知识上考查了函数的零点、利用导数研究函数的性质、不等式的证明等基础主干知识,而能力的考查则更是集数形结合、转化与化归、分类讨论、极限与构造等数学思想和方法,以及运用数学知识进行代数推理求解的综合能力于一体.问题(Ⅰ)考查学生熟悉的函数零点问题,由函数的零点个数确定参数a的取值范围;问题(Ⅱ)则在问题(Ⅰ)的基础上考查函数中的热点——函数与不等式的交汇问题,具有一定的难度.下面逐问分析并解决问题.
【解题思路】由于函数是由几个初等函数复合、叠加或相乘组合在一起的,其形“层峦叠嶂”,其式也“错综复杂”,有时问题又与参数“勾连”,更让学生感觉到“欲度愁攀援”.实际上研究形式较为复杂的函数的零点、极值(最值)等问题,其考查的主旨不变——依旧是利用导数研究相应函数的性质,因而其解题思维流程上也存在一般规律,通常将其转化为探求函数的性质,以期从函数的形态上直观反映函数图象的变化,从而由函数极值与x轴的位置关系得到正确结论.
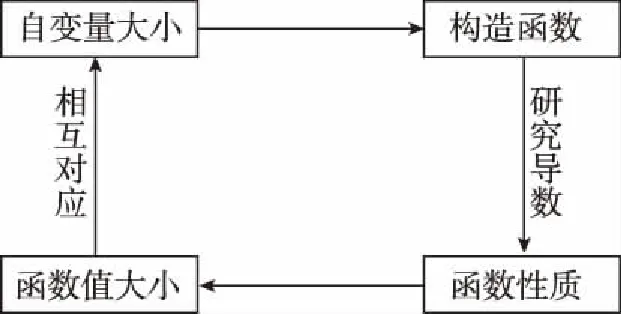
显然本题是含参函数的零点问题,其思维流程图如图.由条件可知,函数f(x)的图象与x轴有两个公共点,故需明确函数的图象升降变化情况,因而应通过其导函数的符号确定函数的单调性,并结合零点存在性定理研究函数零点的可能情形.
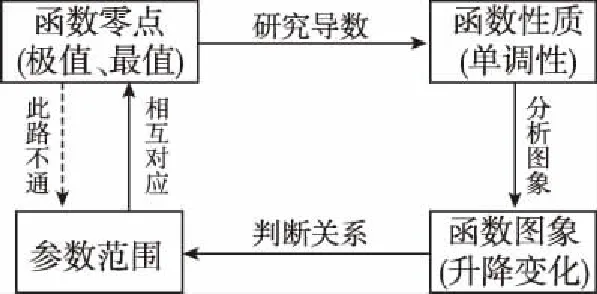
【解法一】(Ⅰ)函数f(x)的定义域为R,且f′(x)=(x-1)ex+2a(x-1)=(x-1)(ex+2a).则由f′(x)=0,得x=1或ex=-2a.
(ⅰ)当a≥0时,则ex=-2a无解.由f′(x)≥0得,x≥1,故f(x)在(-∞,1)上单调递减,在(1,+∞)上单调递增,且f(1)=-e,f(2)=a≥0,则函数f(x)在区间(1,+∞)上存在一个零点x1,且x1∈(1,2].
又当a=0时,函数f(x)=(x-2)ex在区间(-∞,1)上恒为负,此时函数f(x)只有一个零点,不符.


因此,f(x)存在两个零点.
(ⅱ)当a<0时,由f′(x)=0得x=1或x=ln(-2a).

故当x∈(1,+∞)时,f′(x)>0,
因此f(x)在(1,+∞)上单调递增.
又当x≤1时,f(x)<0,所以f(x)不存在两个零点.

故当x∈(1,ln(-2a))时,f′(x)<0;
当x∈(ln(-2a),+∞)时,f′(x)>0.
因此f(x)在(1,ln(-2a))上单调递减,
在(ln(-2a),+∞)上单调递增.
又当x≤1时,f(x)<0,所以f(x)不存在两个零点.
综上所述,a的取值范围为(0,+∞).
1.细析难点窥玄巧
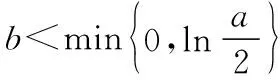
2.熟思细节期远飞
只有深入思考了问题中的一些细节,才能信心满满地鼓翼“远飞”.含参数的导数问题在解答时的根本大法,往往需要对参数进行讨论,虽然是常识,但也是绝大多数学生答题时的易失分点,具体表现在他们不知何时开始讨论、怎样去讨论.对于函数性质的探究,如果没有牢固的“定义域优先”的观念,常会发生忽略定义域而导致出现论域扩大的习惯性错误.而对含参问题的讨论,应思考清楚“为何分类”、“如何分类”,以免面对分类讨论不知所措或盲目分类.需要实施分类讨论是因为研究对象的关系存在不确定性,本题中第一次分类是因为ex>0,而a可能会导致ex=-2a无解,所以依据方程ex=-2a有无解进行分类讨论;第二次分类是因为方程ex=-2a有解x=ln(-2a),与其另一根x=1之间的大小不确定,因而根据两数的大小进行分类.
当分类过多,或解题时运用到不常用的技巧或方法时,总会觉得问题变得烦琐,此时应鼓励学生思考、另辟蹊径避开这些思维上的困扰.如一个函数的零点个数问题可转化为两个函数图象交点的个数.因此思路上的切入方式有参变量全分离和半分离两种.
2.1参变量全分离
使参变量处于“完全分离”状态,转化为研究函数g(x)的单调性仍是常规方式.通过定性求解函数g(x)在不同单调区间上的函数值范围有时“精密度”不够,还需要用上“洛必达法则”严格确定函数的极限,由于所应用的知识超纲,所以这是有风险的.
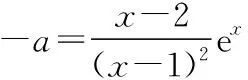

当1 故直线y=-a与曲线y=g(x)有两个公共点等价于-a<0即a>0. 2.2参变量半分离 参变量半分离实际是函数按参数进行整理,将含参代数式与不含参代数式作为两个函数,分离到不等号的两边,通过研究两个函数的变化情况,以确定参数的变化范围.参变量半分离是否有效往往需要我们“未雨绸缪”,考察所研究的函数中含参部分与不含参部分,以及分离后所得到的两个函数的性质是否容易研究. 【解法三】由题意得(2-x)ex=a(x-1)2有两个解,即曲线h(x)=(2-x)ex与y=a(x-1)2有两个公共点.由h′(x)=(1-x)ex≥0得x≤1,则h(x)在(-∞,1)上单调递增,h(x)∈(0,e);h(x)在(1,+∞)上单调递减,h(x)∈(-∞,e).若满足y=a(x-1)2与h(x)=(2-x)ex有两个公共点,则y=a(x-1)2为开口向上的抛物线,故a的取值范围为(0,+∞). 将参变量处于“半分离”状态时,发现其中一部分为熟悉的二次函数,且对称轴x=1恰好过h(x)的极值点,精彩的转化正是桥牌中“打好一手坏牌”的智慧. 可见,参变量分离是解决含参问题的一种较为有效的方法.一般地,含参数的不等式恒成立与能成立(在某区间上有解)问题,通过分离参变量,转化为研究不含参数的函数的最值;含参数的函数在某区间上零点的个数等问题,通过分离参变量,转化为求函数的值域问题. 3.深思变式熟解题 下面给出三道变式.变式1着眼于训练“分类讨论”,变式2侧重于“以曲代直”取点,变式3则倾向于体会“参变量分离”在解题中的作用. 【变式1】已知函数f(x)=2ex-(x-a)2+3,a∈R.若x≥0,f(x)≥0恒成立,求a的取值范围. 【解析】因为f′(x)=2(ex-x+a),令h(x)=2(ex-x+a),则h′(x)=2(ex-1)≥0,则h(x)在[0,+∞)上单调递增,且h(0)=2(a+1). (2)当a<-1时,则存在x0>0,使h(x0)=0且当x∈(0,x0)时,h(x)<0,即f′(x)<0,即f(x)单调递减;x∈(x0,+∞)时,h(x)>0,即f′(x)>0,即f(x)单调递增.故f(x)min=f(x0)=2ex0-(x0-a)2+3≥0,又h(x0)=2(ex0-x0+a)=0,从而2ex0-(ex0)2+3≥0,解得0 由ex0=x0-a得a=x0-ex0,令M(x)=x-ex,0 【变式2】(2017·全国卷Ⅰ理·21改编)已知f(x)=ae2x+(a-2)ex-x,若0 综上所述,当0 【变式3】已知函数f(x)=xlnx-ax-1(a∈R)有两个零点x1,x2,且x1 下面分析问题(Ⅱ),由f(x)=0变形想直接求出x1,x2的表示式,自感“云深不知处”,“横绝峨眉巅”.如果从函数思想角度出发,联系到单调函数的函数值与自变量的大小关系是相互对应的,因此,可以建立如图所示的解题思路流程,通过构造函数,利用函数的性质,确定以结论中的量为自变量的两个函数值的大小关系,从而结合函数的单调性间接确定自变量的大小. 要证明x1+x2<2实质是比较自变量的两个取值之间的大小关系,由函数的单调性可知,在同一单调区间内的自变量的两个取值与其函数值大小存在着对应关系,即函数g(x)单调递增时,函数值大则自变量的值也大;函数g(x)单调递减时,函数值大则自变量的值反而小.因此,x1+x2<2转化为构造函数g(x),由单调性判断函数值的大小. 【证明】不妨设x1 由于f(2-x2)=-x2e2-x2+a(x2-1)2, 而f(x2)=(x2-2)ex2+a(x2-1)2=0, 整理得f(2-x2)=-x2e2-x2-(x2-2)ex2. 构造函数g(x)=-xe2-x-(x-2)ex,x>1,则 g′(x)=(x-1)(e2-x-ex)<0. 即g(x)在区间(1,+∞)上单调递减, 而g(1)=0,故当x2>1时,g(x2) 即g(x2)=f(2-x2)<0, 故f(2-x2) 本题解题顺畅成功的关键在于构造函数g(x)=f(2-x),结合x2为零点消去参数a,转化为f(2-x2)与0的大小关系,再利用单调函数的定义,实现自变量的大小与函数值的大小的转化,最终由函数值的大小间接确定自变量的大小,这是在解与抽象函数有关的不等式时常用的方法,但也是易忽视的一种重要技巧.如果教师方法得当,自会让学生觉得所触之题“依旧秀色照清眸”,在考场上游刃有余. 1.绰约新妆玉有辉,精熟笙歌试羽衣 由上述过程可见,构造函数是解决函数两自变量的大小问题的有效方法,是将难以正面突破的问题转化为可侧面攻击的问题的重要手段.这需要灵活依据结论的代数结果变形,牢牢把握代数式的结构构造函数.其有效途径之一是深入地研究典型题的变式,感受到“绰约新妆玉有辉”,才能在“笑伴笙歌试羽衣”的精熟解决过程中,透彻地掌握同类问题的解法.下面提供的问题中,变式1与例题的构造方法相同,变式2和变式3则将结论变更为零点差、积的形式,考验学生对具体问题进行具体构造的灵活性. 因为x1+2>2,x3>2,所以x1+2>x3,即x3-x1<2. 【解析】注意到结论与已知函数形式之间的差异,则欲证x1x2>e2,应转化为证明lnx1+lnx2>2. 不妨设0 故h(x)在区间(0,e)上单调递增,则h(x)




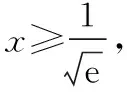


二、云深茫然巧联系,构造函数显秀色