引导学生挖掘信息结构与几何直观——例谈直观想象素养的培养途径

浙江 余继光

一、直观想象中的信息结构

1.直观想象是指借助空间想象感知事物的形态与变化，利用几何图形理解和解决数学问题.主要包括：利用图形描述数学问题，建立形与数的联系，构建数学问题的直观模型，探索解决问题的思路.直观想象是发现和提出数学命题、分析和理解数学命题、探索和形成论证思路的重要手段，是构建抽象结构和进行逻辑推理的思维基础，是培养创新思维的基本要素.通过直观想象核心素养的培养，学生能够养成运用图形和空间想象思考问题的习惯，提升数形结合的能力，建立良好的数学直觉，理解事物本质和发展规律.

2.直观想象建立在信息结构的基础上，只有认准或挖掘出信息中的结构特征，才能准确呈现其几何直观，因此直观想象的基础是数学知识的本质特征.

3.直观想象的引导力在于对问题信息结构的分析与启发，一是养育这一意识，面对具有明显特征的信息，问自己这里隐藏着几何直观吗？二是储备信息结构与几何直观间的关联；三是大胆挖掘，细心验证.

二、直观想象中的引导策略

1.大胆“挖”——任何信息结构，只有充分挖掘，才能显示其本来面貌，在教学中引导学生积极大胆实践非常重要，这一意识是培养学生的直观想象力的重要一点.

2.细心“验”——挖掘出来的几何直观是否真是问题的本质，还需要细心检验，这是引导学生做学问必备的素养.

3.善于“思”——慎思、深思、有兴趣的思，而不是仅仅为了完成作业消耗精力的思，这才是数学教学的落脚点！

三、直观想象中的教学途径

1.从代数结构中挖掘“代数”与“几何”直观

数学是一门形式科学，它研究的是抽象元素之间的“关系”和“运算法则”.这些“相互关系”和“运算法则”构成了数学 “结构”.从代数信息结构上挖掘直观，是养育学生直观想象能力的最佳途径之一.

分析：本题给定的题设信息结构为“○2+○△+△2”，从代数公式结构上与立方差公式可直观想象；由余弦定理表达式也可直观想象，于是有了下列思考.

解法一：从代数结构中寻找变元关系.

由①可得，x3-y3=(x-y)(x2+xy+y2)=x-y,

由②可得，y3-z3=3(y-z),

由③可得，z3-x3=4(z-x),

以上三式相加，z=3x-2y，代入②得3x2+y2-3xy=1，

与①联立，解得2x(x-2y)=0，因为x>0，所以x=2y,

解法二：挖掘代数结构中几何意义，由余弦定理可得

x2+xy+y2=x2+y2-2xycos120°=12,

z2+zx+x2=z2+x2-2xzcos120°=22,

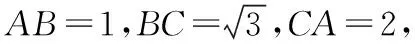
在△ABC内取一点P，使∠APB=∠BPC=∠CPA=120°,如图1，

由原题条件可知，PA=x，PB=y，PC=z是原方程的一组解，

将△APC绕C点顺时针旋转60°，得△A1P1C，如图2，则△PP1C为正三角形，所以A1,P1,P,B共线，则x+y+z=PA+PB+PC=A1B，∠A1CB=∠P1CA1+60°+∠BCP=∠PCA+60°+∠BCP=60°+30°=90°，所以△A1BC为直角三角形，

解读：解法一是从代数结构中寻找变元之间的联系“x3-y3=(x-y)(x2+xy+y2)”——“代数直观”，从解方程的角度寻找突破；解法二是根据给定方程组的代数结构“x2+xy+y2=1”上发现“几何直观”，通过构造几何图形来实现突破！

素养水平：能够在熟悉的数学情境中，借助图形的性质和变换(平移、对称、旋转)发现数学规律；能够描述简单图形的位置关系和度量关系及其特有性质，方程组变量间的结构与余弦定理的结构间的联系是条件挖掘的着力点；能够通过图形直观认识数学问题，能够用图形描述和表达熟悉的数学问题，启迪解决这些问题的思路，体会数形结合.

2.用换元来呈现代数结构的几何直观背景

善于挖掘数学信息的几何直观背景本身就是一个数学文化素养高的特征.当信息的结构与几何直观不易发现时，可能一个小的动作，比如“换元”就使之直观凸显，便于进一步的思考.

分析：题设信息中呈现无理式，不易发现其结构，通过换元，变无理为有理，探究其几何直观.

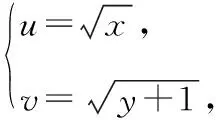
上式可化简得(u-1)2+(v-1)2=3(u≥0,v≥0),

(1)

则x+y=u2+v2-1.

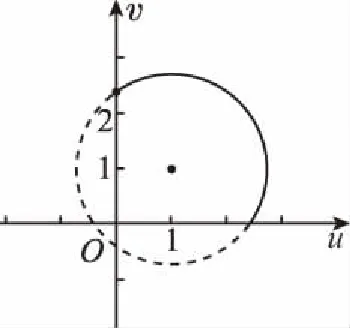
解读：由无理换元后为有理式，这是受过数学训练者的自然思维途径，关键是遇到“u2-2u=2v-v2+1”后，从代数结构上发现其几何直观——一段圆弧.而目标正是要求这一段弧上的点到原点距离平方再减1的最大值.

素养水平：能够在关联的情境中，想象并构建相应的几何图形；能够借助图形提出数学问题，发现图形与图形、图形与数量的关系，探索图形的运动规律.

3.用构造图形的方式来培养直观想象

构造思想是一种创新思维，面对代数结构式的特征，运用直观想象能力将其转化为几何问题，从而简化代数运算，这也是培养直观想象素养的途径之一.

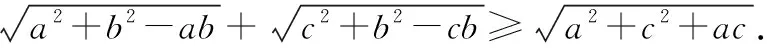
证明：构造如图，设AB=a，AC=b，AD=c,∠BAC=∠CAD=60°，∠BAD=120°,

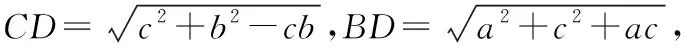
因B,C,D三点可能构成三角形或三点共线，所以BC+CD≥BD,

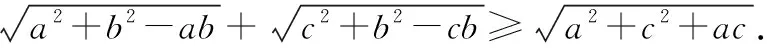
解读：本题目标代数式看似一个轮换式(右端有一点差异)，而且每一个式子的结构都是学生比较熟悉的余弦定理式，通过构造几何图形，运用几何方法证明是一个智慧的选择，这正是直观想象的美妙之处！

素养水平：能够在熟悉的情境中，抽象出实物的几何图形，建立简单图形与实物之间的联系；体会图形与图形、图形与数量的关系；能够在熟悉的数学情境中，借助图形的性质和变换(平移、对称、旋转)发现数学规律；能够描述简单图形的位置关系和度量关系及其特有性质，能够通过图形直观认识数学问题，能够用图形描述和表达熟悉的数学问题，启迪解决这些问题的思路，体会数形结合.

4.展示向量的几何特征来直观想象

向量是既有代数特征又有几何特征的量，向量的模、向量的加、减、数乘运算以及数量积都有其独特的几何背景，对于向量问题充分展示其几何特征，引导学生挖掘其几何背景也是培养直观想象的途径之一.

【例4】已知共面向量a,b,c满足|a|=3,b+c=2a，且|b|=|b-c|.若对每一个确定的向量b，记|b-ta|(t∈R)的最小值为dmin，则当b变化时，dmin的最大值为

( )

分析：此题条件中涉及到向量的模的条件较多，它是几何直观的表现形式的基础，再加上向量运算的几何直观，于是通过展示向量几何特征的方式来探寻突破.

所以x的最大值为2，即dmin的最大值为2.

解读：抓住“|b-ta|(t∈R)”的几何意义，并探求其最小值的几何意义就是点到直线的距离，使问题的几何直观想象有了着落，巧妙地运用三角知识搭建变量之间的关系也体现了代数直观的要素.条件“|a|=3,b+c=2a，且|b|=|b-c|”的几何背景是“等腰三角形一腰上的中线长为3”，条件“|b-ta|(t∈R)的最小值为dmin”的几何意义是“中线上的点与等腰三角形顶点之间距离的最小值应该是顶点到中线的距离x”，通过几何图形的挖掘转化为三角与代数问题求解，变形与计算量较少.

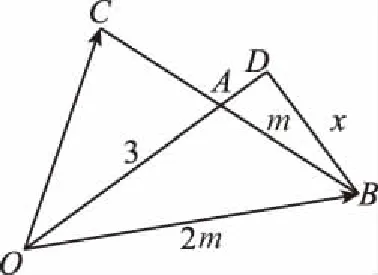
分析：题设中的每一个信息都有其几何意义，充分梳理其几何背景画出直观图形，基本上就解决了此问题！

信息“c与a-b所成的角为120°”说明∠ADC=120°,

从而∠ODB=60°.

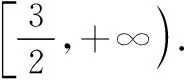
解读：向量问题是直观载体最丰富的一类问题，稍微动用一下想象就可将问题的本质挖掘出来，所以通过向量运算或性质研究来培养学生的直观想象能力是最普遍的策略！