环状周期结构面外参激振动稳定性分析
2018-08-02杨玉虎杜爱伦王世宇
杨玉虎,杜爱伦,王世宇,
(1. 天津大学机械工程学院,天津 300072;2. 天津市非线性动力学与控制重点实验室,天津 300072)
环状结构广泛应用于工程实际中,例如轴承的内外圈、旋转电机的定转子以及行星传动的齿圈等.在工作过程中,该类结构通常受接触或非接触、均布或离散载荷的作用,产生振动和噪声,同时降低工作效率,甚至发生永久破坏而导致事故.因此,研究该类结构的振动及其抑制措施尤为重要.目前,大量研究通常仅限于面内振动,具体内容涉及自由振动、受迫振动、参激振动以及非线性振动等方面.专门针对环状周期结构的面外振动研究相对较少.
环状周期结构通常可分为单、双环结构.其中,单环结构十分常见,理论研究也较为深入.Kim 等[1]研究了旋转圆环的面内和面外自由振动和非线性振动,比较了非线性与线性模型,得到了较为准确的应力-应变关系.同时指出:由于旋转作用增大了圆环的刚度,因此不存在失稳现象.Canchi等[2-4]和 Wu等[5]以行星传动为背景,研究了环状结构的动力学特性.其中,Canchi等[2-3]研究了受移动载荷作用的静止和旋转圆环的参激稳定性,采用多尺度法揭示了结构参数与不稳定边界的映射关系;他们还给出了啮合相位和重合度等基本参数与稳定性之间的关系,为齿轮系统的参数设计提供了理论借鉴.Wu等[5]采用微元法建立了圆环的面内振动模型,探讨了固有频率分裂及振型耦合规律.此外,Lesaffre等[6]研究了受移动支撑激励的圆环振动特性,采用 Routh-Hurwitz判据研究了稳定性问题.Sadeghi等[7]采用多尺度法研究了由时变内应力导致的圆环稳定性问题.
旋转电机的定转子也可视为受移动载荷的环状周期结构.磁致振动和噪声问题一直是该领域的重要研究内容.Xie等[8]采用能量法建立了双定子电机转子的二维动力学模型,分析了磁致弹性振动问题.Xia等[9]在磁场同步坐标系下建立了机-电-磁三场耦合动力学模型,通过求解特征值研究了三相对称感应电机定子的振动规律,揭示了机、电和磁参数与动力稳定性的映射关系,同时证明了即使三相对称仍然存在发散和颤振不稳定现象.Zhao等[10]建立了永磁电机定子的弹性动力学模型,采用多尺度法和Floquét理论研究了磁致参激振动规律,揭示了基本参数对不稳定域的影响规律.应当指出,由于现有文献通常在惯性坐标系下建模,因而得到的参激数学模型含时变系数,不存在解析解,只能采用近似或数值方法求解.其中,摄动法只适合弱参激系统,而数值方法计算效率较低,且通常为个案分析,很难揭示普遍规律.
本文拟研究受面外旋转载荷激励的环状周期结构的参激弹性振动规律.首先采用能量法[1-2,10-13]和坐标变换法分别在载荷随动坐标系和惯性系下建立含轴向弯曲和切向扭摆振动的二维模型,然后应用经典振动理论计算特征值,从而预测动力稳定性,最后采用Floquét理论验证了解析结果的正确性.
1 数学建模
1.1 模型描述
图1为旋转环状周期结构及采用的坐标系.圆环的轴向高度、径向厚度、密度、弹性模量、剪切模量和中性圆半径分别为 h、b、ρ、E、G 和 R.OrθZ 和OρφZ分别为惯性和支撑随动坐标系,原点位于几何形心.O′xyz为截面坐标系,原点位于中性线上.x、y和 z分别沿径向、切向和轴向.仅考虑面外振动,w表示中性面上任意一点的轴向位移,且为角度θ和时间 t的函数.与圆环垂直且等间隔分布的旋转支撑kj(j=1,2,…,N,N 为支撑个数),刚度均为 ks且转速为Ω.不失一般性,假设第1个支撑的初始位置位于极轴,因此两种坐标系下第j个支撑的初始位置分别为
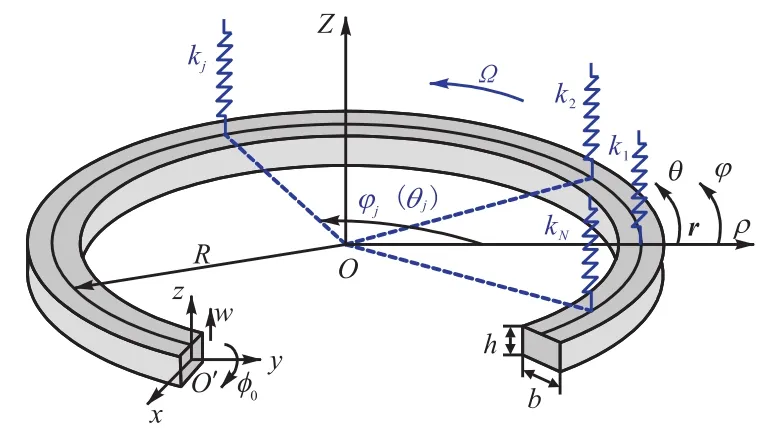
图1 旋转环状周期结构及坐标系Fig.1 Rotational ring-shaped periodic structure and coordinates
1.2 支撑随动系建模
本节在图1所示随动系下采用能量法建模.取圆环截面任意一点分析,假设该点的坐标为(x, z),θφ、φr、φz分别为该点的切向、径向和轴向转角,该点的位移为uθ、ur和uz.在支撑随动坐标系下,该点的位置矢量为
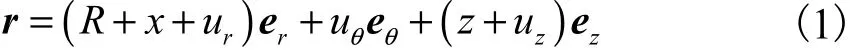
式(1)关于时间求导,有

其中
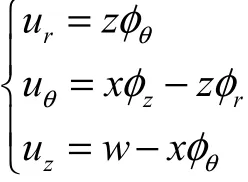
由于w和φθ是关于(ϕ*,t)的函数,ϕ*是随动坐标系下的切向坐标,考虑旋转作用,有ϕ*=ϕ−Ωt,则

又
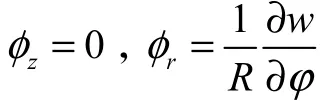
因此
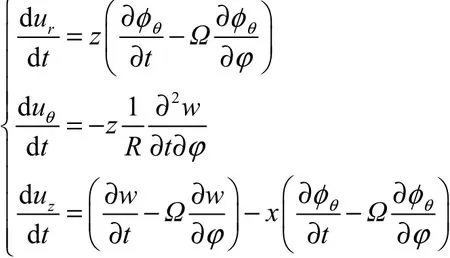
将上式代入式(2)可得圆环动能
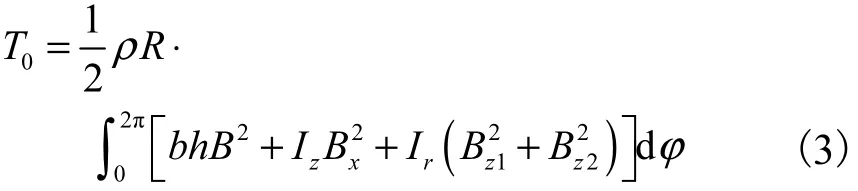
式中:Ir( Ir= bh3/12)和Iz( Iz= b3h /12)分别为绕 x轴和z轴的截面惯性矩;B、Bx、Bz1和Bz2分别为
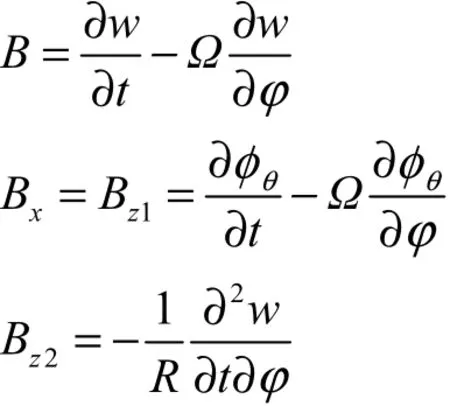
根据薄环假设,在空间应变状态下中性面上的任一点的切向应变[14]为

式中为截面中心切向应变,且
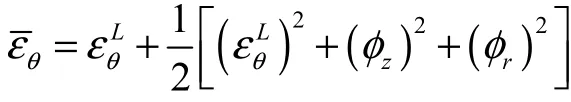
为由圆环变形引起的曲率改变量,此处为0.又
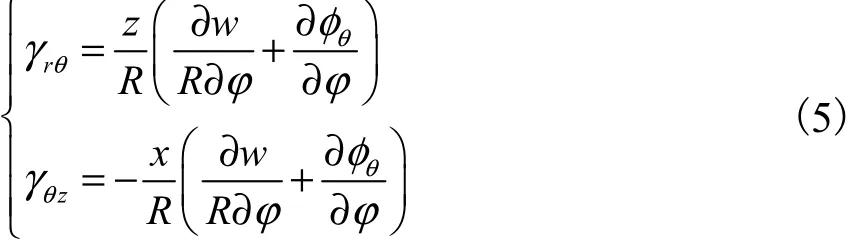
综合式(4)和(5),可得圆环的应变能
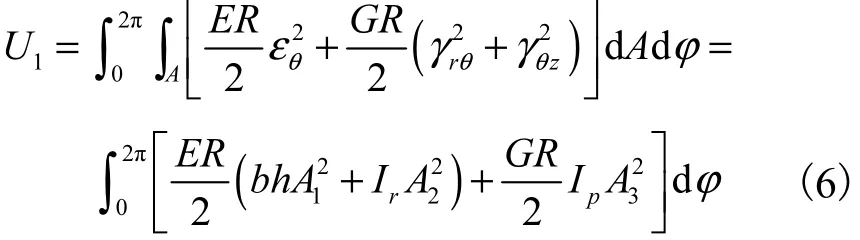
式中:Ip( Ip= bh( b2+h2)/12)为圆环截面惯性矩;A1~A3分别为

旋转支撑的弹性势能为

式中:δ为狄拉克函数;q′为整数,其作用为保证
根据Hamilton原理可得

将式(3)、(6)和(7)代入式(8)中,可得动力学方程.引 入 无 量 纲 运 算 Ωs=TΩ、=t/ T、=w/ R、=φθ/R和= ksR/( E A),可得无量纲动力学方程.为书写方便,将Ωs、和分别替换为Ω、t、w、φθ和ks,可得含陀螺项的偏微分方程为

其中

式中:M ′和 K ′0分别表示支撑随动坐标系下光滑圆环的质量和刚度矩阵算子;K ′1为旋转离散支撑产生的附加刚度矩阵算子.
采用 Galerkin方法对式(9)进行离散[15],为此,选取一个满足圆环边界条件的形状函数 einϕ,构造轴向弯曲振动和切向扭摆振动响应.首先假设

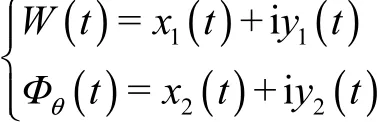
定义内积运算

将式(10)代入式(9)中,并与 e−inϕ做内积,分离实、虚部,然后写为矩阵形式,可得

其中

根据三角函数的运算性质,有

若2n/ N不为整数,则旋转支撑的激励作用消失,系统始终处于稳定状态,故此处不做具体讨论;若2n/ N为整数,则
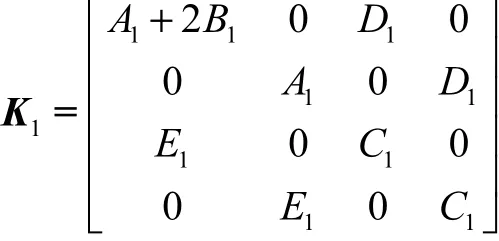
其中
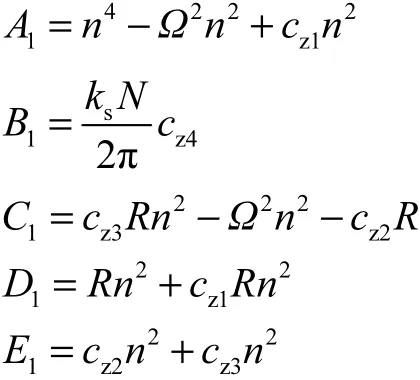
由于式(12)为常系数微分方程,可直接求解出特征值,进而预测系统的动力稳定性.
1.3 惯性系建模
针对旋转支撑随动坐标系 OρφZ下的非时变运动方程(9),引入坐标变换θ=ϕ+Ωt,可将其转换至惯性坐标系OrθZ下,得到时变运动方程

其中

2 数值仿真
为了确定系统的参激振动特性及稳定性,可根据式(12)计算特征值.为此,假设

则

式中:x(t)为 8×1的状态矩阵;B为 8×8的周期矩阵;0和I分别表示4×4零矩阵和单位矩阵.假设

式中λ为系统特征值.将式(16)代入式(15)中,可得特征方程

表1给出了一个典型旋转环状周期结构的基本参数,其中圆环的径厚比满足薄环条件.如果没有特别指出,下文所用参数均取自表1.

表1 环状周期结构基本参数Tab.1 Specifications of a ring-shaped periodic structure
根据式(16)计算出的特征值进行仿真,可得图2和图3所示特征值实、虚部随转速的变化规律以及波数、支撑刚度及其个数的影响.需要指出的是,图中所示情形均满足2n/N为整数的条件.
图2中蓝线和红线分别代表系统的 1、2阶特征值,且分别对应弯曲和扭摆振动,其中实线和虚线分别为正、余弦模态.可以看出,当结构静止时,各阶特征值的虚部均不为零,且数值随波数而增大;若支撑刚度增大,则 1、2阶余弦模态的特征值虚部随之增大,但正弦模态数值均无变化.当旋转支撑转速较大时,各阶特征值正、余弦模态均不重合,产生分裂现象[16],且在振动波数相同的前提下,支撑刚度越小,分裂越显著.总体来看,在较低转速范围内,各阶特征值虚部受支撑刚度影响较大,但随着转速上升,波数更容易影响虚部数值及变化趋势.
根据特征值实部可预测系统的稳定性.若实部大于零,则响应随时间发散,因而不稳定.由于不稳定现象通常涉及1阶模态的弯曲振动,因此低阶振动普遍受到重点关注.从图3可以看出,当波数增加时,不稳定区域范围减小,并且出现的位置更加聚集;当支撑刚度增大时,引起不稳定的转速区间明显扩大且不稳定程度显著增强.在工程实际中,应当合理选择设计参数,使工作转速远离不稳定区域.

图2 特征值虚部随旋转支撑转速的变化规律Fig.2 Imaginary part of eigenvalue versus rotation speed of rotating supports

图3 特征值实部随旋转支撑转速的变化规律Fig.3 Real part of eigenvalue versus rotation speed of rotating supports
图4描述了不稳定域随波数的变化规律.对比图2(a)可知,图4(a)中左侧第 1个不稳定域的“尖点”位置对应的1阶正弦模态的特征值虚部为零,因而为发散不稳定;同理,第2和第3区域均为发散不稳定,无颤振不稳定现象.同理,图4(b)和图2(b)有相同的对应关系.

图4 不稳定域随波数的变化规律Fig.4 Unstable regions versus wave number
为了进一步验证不稳定域及其类型的正确性,在图4(a)中的稳定和不稳定区域任意选取 3组参数{ks=0.7,Ω=8}、{ks=0.7,Ω=18}、{ks=0.1,Ω =8},在其他初始条件均相同的情况下,采用变步长龙格-库塔方法分别求解时域响应,可得图5所示结果.其中蓝线和红线分别对应轴向弯曲和切向扭摆振动的响应.可以看出,图5(a)和(b)均呈现发散特征,图5(c)和(d)则呈现周期特征.显然,数值计算与理论预测结果相符.

图5 时域动态响应Fig.5 Time-domain dynamic response
3 数值验证
为了进一步验证上述结果的正确性,本节基于Floquét理论,针对惯性系下的时变动力学模型进行数值计算,预测系统的动力稳定性,进而验证坐标变换方法及支撑随动坐标系下解析结果的正确性.采用式(10)的设解形式对式(13)进行Galerkin离散,可得

其中
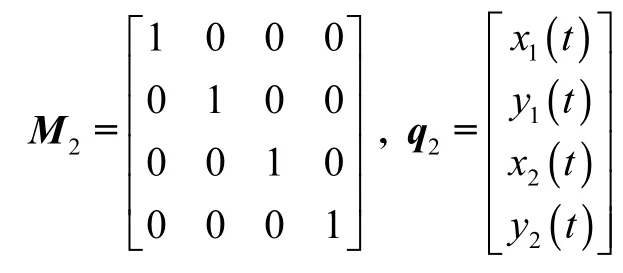

将式(18)改写为状态空间形式,可得
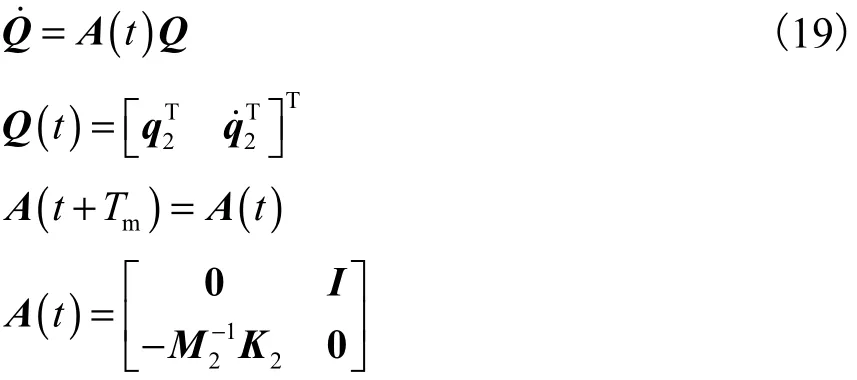
式中:Q为8×1的状态变量矩阵;A(t)为8×8的时变周期矩阵;Tm是与支撑转速相关的激励周期.根据A( t)可近似构造 Floquét转换矩阵,然后根据特征乘子判断系统的动力稳定性[15,17].具体计算结果如图6所示.
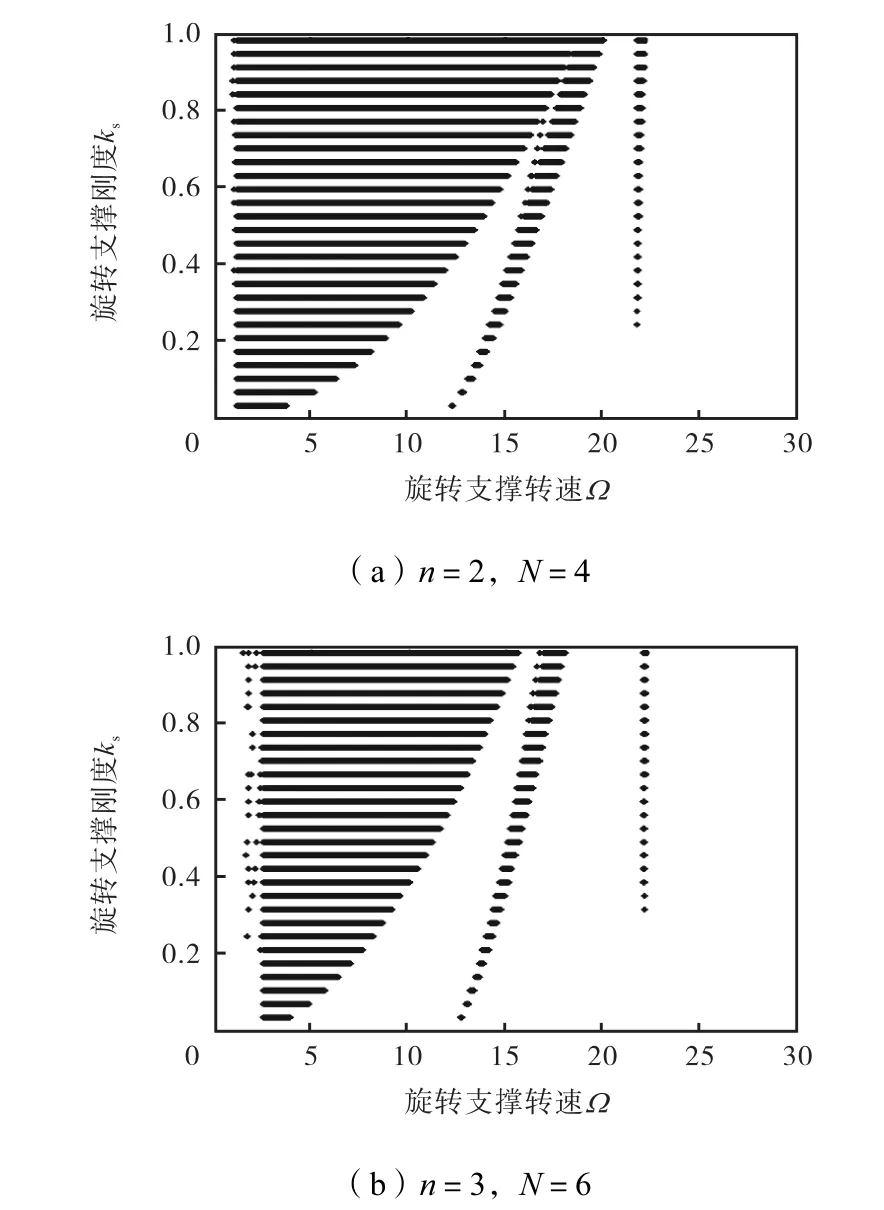
图6 不稳定域预测Fig.6 Estimation of unstable regions
对比图4和图6可知,在忽略计算误差的前提下,两个坐标系下的计算结果一致,从而验证了随动系下得到的不稳定域位置及其边界的正确性.
4 结 论
(1) 采用 Hamilton原理在载荷随动坐标系下建立了描述轴向弯曲和切向扭摆振动且含定常系数的弹性动力学模型.
(2) 根据特征值预测了系统的动力学特性,具体分析了动力稳定性及其类型,揭示了发散不稳定现象及其变化规律.
(3) 采用Floquét理论在惯性坐标系下计算了动力稳定性,从而验证了载荷随动坐标系处理方法的正确性.
