基于Sobol序列的防尘供水管网系统可靠性分析

邓权龙，蒋仲安，韩 硕，付恩琦

(北京科技大学金属矿山高效开采与安全教育部重点实验室，北京 100083)

矿井防尘供水管网作为保障矿山井下安全生产的基础设施，为井下采掘工作面粉尘防治工作提供重要支持，其能否正常有效运行直接关系着矿山工人的职业健康．井下防尘供水管网所处的井下环境较为恶劣，受到高压、高湿、高腐蚀等因素影响，担负长时间持续供水的任务，此外，供水管网本身的结构具有复杂性，维护难度大，所以，有必要对矿井供水管网系统可靠性做进一步量化研究，用科学分析方法评估其可靠性．

国内外学者对供水管网可靠性研究主要集中于城市供水管网，对矿井供水管网系统可靠性研究报道较少．目前，在供水管网可靠性研究方面，较主流的方法[1]主要有代理法、解析法、模拟法．代理法主要有信息熵法[2]、剩余能量熵[3]、可恢复性指标法[4]等；解析法主要有故障分析法[5]、最小割集法[6]、一次二阶矩阵法[7]等；模拟法主要包括蒙特卡罗法[8-9]、拟蒙特卡罗法[10-11]等．针对矿山井下防尘供水管网多为树状分布的特点，笔者将解析法和模拟法相结合，综合考虑路径重要度和连通率，提出了对管网系统可靠度的解析求解法；并为了避免传统的蒙特卡罗法伪随机数序列求解的收敛速率慢、求解精度不够等缺点，采用 Sobol序列的拟蒙特卡罗法对管网单元故障次数进行抽样，最终求解管网系统可靠度．

1 可靠性计算模型

矿井防尘供水管网主要由水池、水泵、阀门、用水点、水管以及管段连接部件等组成，经简化并忽略管网内部结构微小的差别，可以将矿井供水管网认为是节点和边按照一定规则连接组成的集合，边代表连接节点的管段，节点代表用水点、水源、管段连接处等．矿山井下防尘供水管网大多数为树状分布管网，如果将每根管段流量赋予该边作为权值，则矿井供水管网实质上是一棵以水源为根的有向树．对于矿井供水管网可靠度的求解可以转化为树状网络可靠度求解的问题．

由于树状管网中任意两个节点之间有且仅有一条路径，对于任一用水点与水源处只有一条路径，所以矿井供水管网网络可靠度的定义为：在规定条件和规定时间内，水源以规定的流量输送至各个用水点的概率[12-13]，R＝P｛水流以规定的流量从水源到达各个用水点｝．

若供水管网网络某节点或边发生故障后，水流不一定能以规定流量到达用水点，管网网络的可靠度必然受到影响，为了深入量化求解供水管网系统可靠度，引入流可靠度与阈级、重要度、连通率的概念．

建立矿井防尘供水管网可靠性计算模型时需要先进行2个假设：①管网单元只有正常和失效两种状态之分；②管网单元故障率 λ和修复时间 Tr都是常数，单元失效、修复彼此独立．

1.1 流可靠度与阈级

供水管网中赋权的单元发生故障时，设定流或权值受到影响，不能到达规定的目的地．但是，在网络中，其他完好路径部分中的流是能够到达目的地．因此，定义流可靠度为：在一个网络中，当某单元发生故障时，到达规定目的地的流与网络正常时完全到达目的地的流之比，用u表示．

设矿井供水管网为 G，用 Q表示单位时间内到达各个用水点的总水量．当供水时间为 T时，则供水管网传输至用水点的总水量为

若管网中某一单元 e发生故障且故障持续时间为 ΔT，而其他单元在供水时间 T内均正常供水，则供水管网能够传输至用水点的总水量为

在可靠性求解方面，阈级代表的实际含义为网络某单元故障对管网中输送至用水点水量的影响程度.

1.2 重要度

在整个供水管网网络中，由于网络的拓扑结构和管段流量不同，每个单元在网络中扮演角色的重要程度均不同，对整个供水管网的影响程度也不同．当管网中某些管段、节点故障失效时，对管网网络整体的可靠性影响较小，而其他管段、节点发生故障时，对管网可靠性影响较大．为合理、科学量化供水管网中各个单元重要度，借鉴基于阈级的单元重要度的理念，用来衡量各组件对管网可靠性影响的重要程度．

假设供水管网中共有m个单元，单元i的重要度Ii可以表示为

定义管网有效路径为以水源节点为起点且需水点为终点的管路路径，管网中有效路径条数等于需水点的个数．每条有效路径由多个单元(节点、管段)组成，设管网中总共有 x条有效路径，则有效路径 k的重要度Lk为

1.3 连通率

在树状矿井供水管网中，用水点到水源只有唯一路径，由节点和边组成，一旦位于路径上的某一单元故障，该路径将受到影响，影响路径的连通性，所以有必要对路径的连通率进行量化分析．组成供水管网系统单元主要包括节点和管段，若管网系统某一单元i正常工作的概率为Pi，单元故障修复的平均时间为 Tr，若分析时间为 1,a(365,d)，设该时间段内发生故障的次数为 ni，则管网中单元 i的正常工作的概率为

定义路径连通率为路径上所有单元同时正常工作的概率，那么有效路径k的连通率Pk可表示为

1.4 管网系统可靠度

矿井防尘供水管网系统可靠性就是保证管网中所有需水点与水源连通并达到规定流量的概率．将供水管网路径重要度和路径连通率相结合，求解出供水管网系统可靠度

式中Lk为管网中有效路径k的重要度．

2 基于Sobol序列的供水管网系统可靠性求解

2.1 拟蒙特卡罗法的Sobol序列

拟蒙特卡罗法求解问题的主要思路[14-16]为：首先建立与问题相关的概率模型或随机过程，通过对概率模型或随机过程的观察或抽样试验计算所求的随机参数的统计特征，依据求解精度或者次数要求，得到目标的求解近似值．与传统的蒙特卡罗法相比，拟蒙特卡罗法采用低偏差数序列对问题模拟求解．低偏差数序列能保证产生点列有更强的均匀特征，避免了伪随机序列的随机特征，在仿真模拟中，既能够保证解算结果的精度和稳定性，又能够提高收敛速度．

拟蒙特卡罗法经过多年的发展，统计学者们提出多种低偏差序列，常见的有 Halton序列[17]、Niederreiter 序列[18]、Sobol 序列[19]等．每种低偏差序列在点列产生的方法均不同，但都能保证无随机的均匀分布特征．

本文采用 Sobol序列对矿井防尘供水管网系统可靠性进行求解，Sobol序列的构成过程如下[20]．

设mi是小于2i的正奇数，则

式中vi的构成是借助于功能多项式的形式产生的，该多项式为

对于i＞p，存在递归公式

式中⊕表示二进制中的按位异或运算，即 1⊕0＝0⊕ 1＝1，1⊕ 1＝0⊕ 0＝0．对于 mi，对等的递归公式为

存在任一整数 y(y为十进制数)，能够唯一表示为与数基b＝2相关的表达式

式中k表示大于等于lb y的最小整数；aj取值 0或1．则Sobol序列的第z个元素通过式(15)产生．

为了加快序列的产生速度，Antonov和Saleev提出了Gray code法[21]，可将式(9)修正为

式中i为满足aj＝0的最小的j．

Sobol序列在近些年的应用较为广泛，其序列构造方法简单，点列的均匀性较好．图1和图2分别为在1,cm×1,cm的面域内抽样1,000次的伪随机数序列和 Sobol序列的二维分布图，不难看出，伪随机数序列容易出现局部团簇现象，Sobol序列具有较好均匀分布特征．

图1 伪随机数序列二维分布(抽样1,000次)Fig.1 Two-dimensional distribution of pseudo-random number sequence(sampling 1,000,times)

2.2 求解流程

矿井供水管网系统可靠度求解流程如图3所示.

步骤1 计算供水管网中各个路径重要度Lk．根据各个需水点的需水量可得到管网总需水量，由各个单元故障时管网需水量求得单元阈级，由式(5)求得单元重要度，再由式(6)求得各路径重要度．

步骤 2 确定供水管网单元故障率．供水管网网络中单元故障概率较小，参考相关文献与统计资料[10,12]，单元故障次数的分布规律接近泊松分布．

用xi表示管段i在1,a内发生故障的次数，则

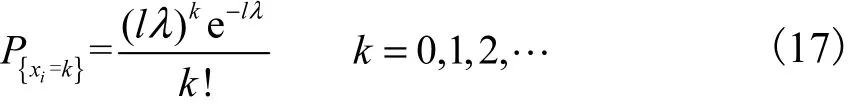
式中 l为管段 i的长度，km；λ为管段 i的故障率，km-1．

用xj表示节点j在1,a内发生故障的次数，则

式中Q为节点j的流量，m3/h；δ为节点j的故障率，m-3·h

步骤 3 确定模拟次数，即样本抽样次数．依据求解精度得到模拟次数N，构造数量为N的Sobol序列，以便后续求解．

步骤 4 计算各路径连通率 Pk．根据每次样本抽样结果得到各个管段发生故障次数，由式(7)求解各管段1,a正常工作的概率Pi，计算各路径的连通率.

步骤 5 计算供水管网系统可靠度 R(G)．根据式(9)求得管网系统可靠度．

步骤 6 判别结果收敛程度、抽样次数是否到达预设的要求．每进行 1次抽样，都求得对应的管网系统可靠度，观察多次抽样结果，判断结果是否收敛，抽样次数是否达到要求．若判断结果为否，则循环步骤2～5；若判断结果为是，则进入下一步骤．

步骤 7 进行 N次计算的可靠度结果统计与分析．

图3 供水管网系统可靠度求解流程Fig.3 Solution process of water supply network system reliability

3 实例应用

将该可靠性分析模型应用于开滦集团某煤矿井下防尘供水管网，该矿供水管网以－50,m处静压水池作为主要供水水源．经过对管网简化，管网中共有28个节点、27个管段、10个需水作业点，各个作业点需水量详见表 1．矿山井下防尘供水管网基本信息见图4．管网节点、管段参数信息详见表2和表3．

表1 矿山井下作业点需水量Tab.1 Flow water of mine underground working faces

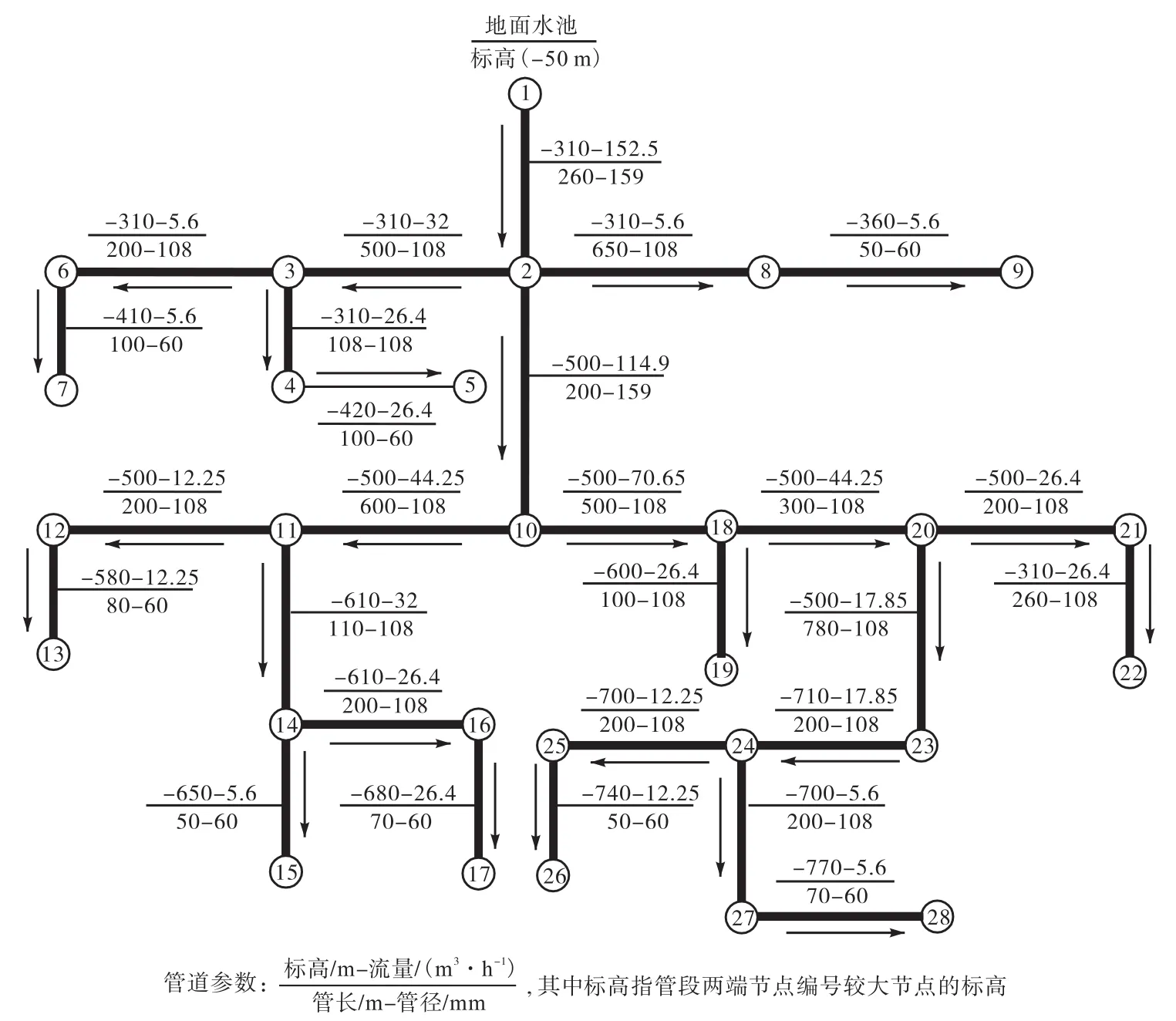
图4 矿山井下防尘供水管网基本信息Fig.4 Basic information of mine dust-proof water supply network

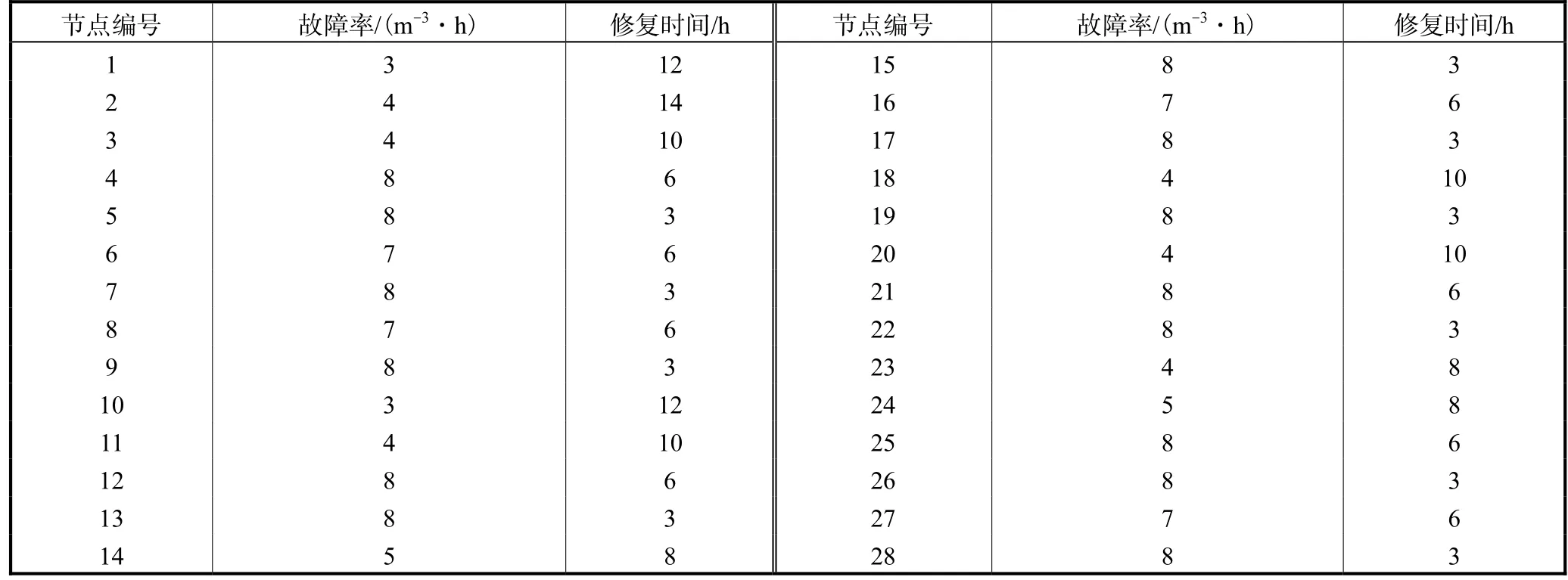
表2 节点参数信息Tab.2 Parameter information of nodes

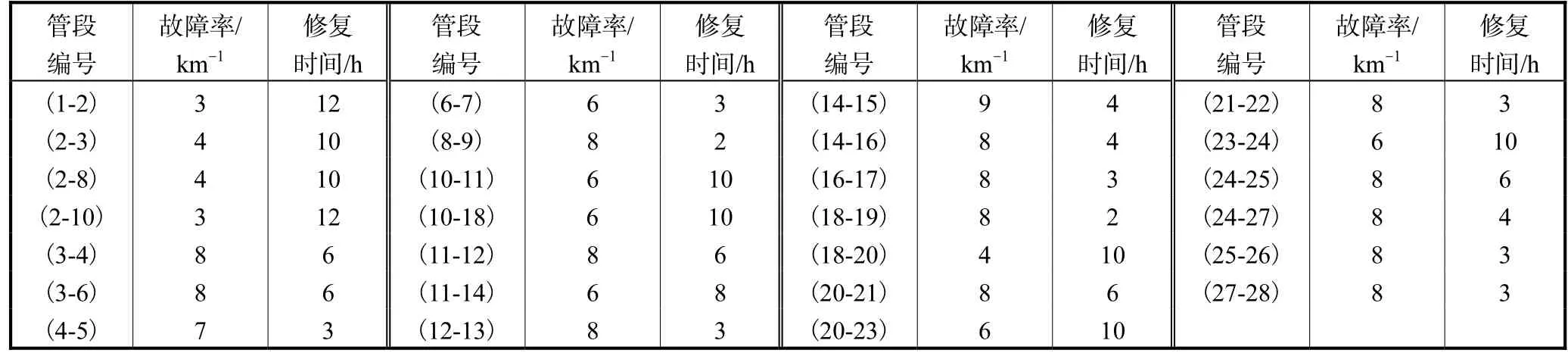
表3 管段参数信息Tab.3 Parameter information of pipes

首先，根据各个作业工作面用水点的需水量，分别计算各个节点、管网故障时能够保证作业点水量总和，得到单元阈级，再代入式(5)求得单元重要度及各个节点、管段阈级和重要度，如表4和表5所示．从表4和表5中可以看出，当单元故障时，其阈级越低，对供水管网网络的影响程度越大．管段中流量越集中时，管段故障时阈级越小，其在供水网络的重要度越高，同时对网络可靠性影响程度越高．

所以在管网规划设计时，为了提高管网网络系统的可靠性，应尽量避免管段流量过度集中，在条件允许下分散管网管段流量．流量过于集中时，一旦发生故障，对网络的影响程度将会很大，网络整体可靠性随之降低．此外，在管网维护时，应当根据不同单元的重要度采取不同程度的加固措施．

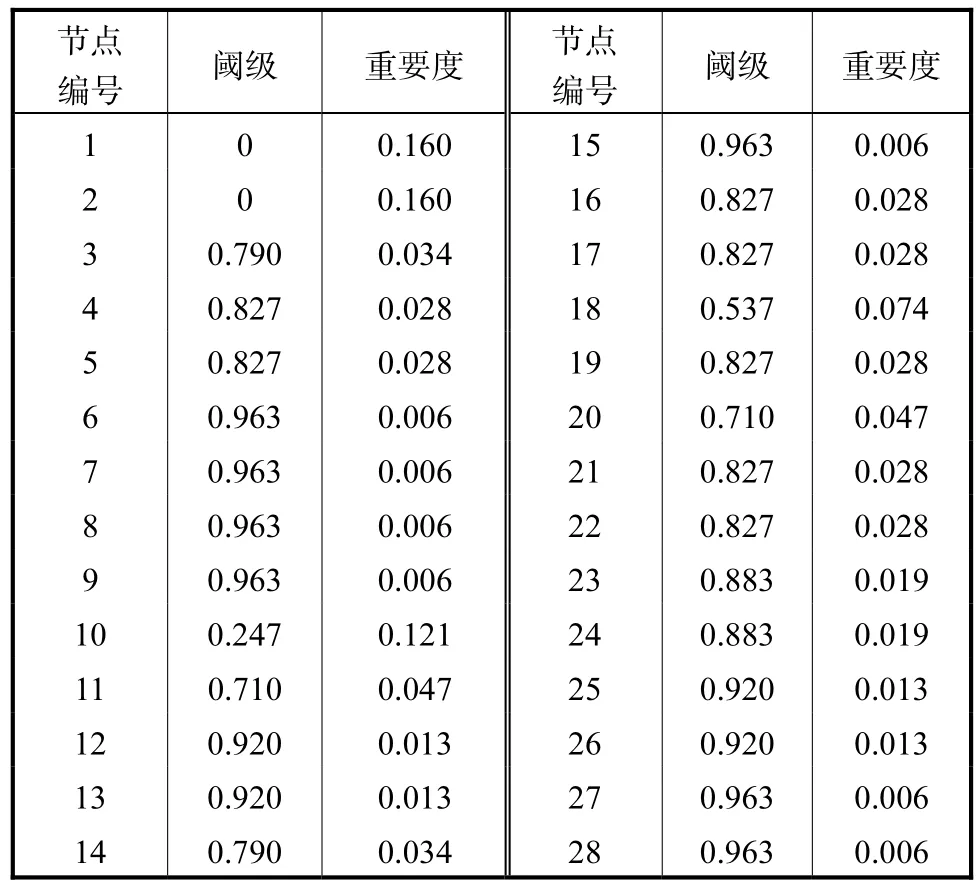
表4 节点阈级和重要度Tab.4 Threshold level and importance of nodes

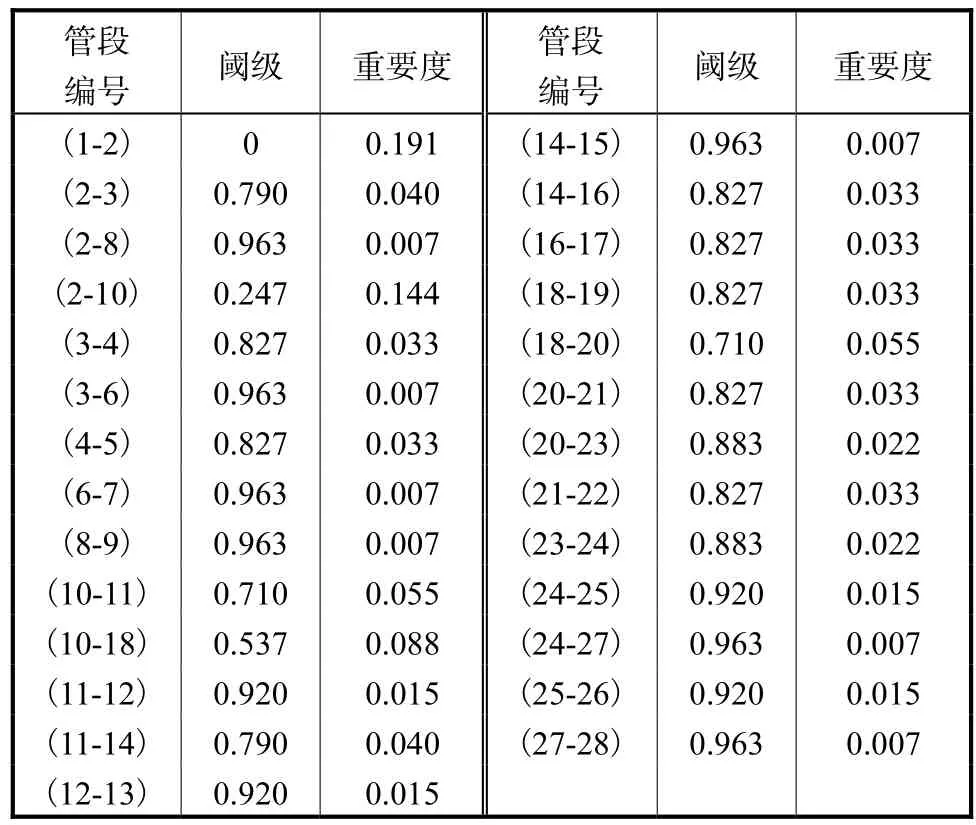
表5 管段阈级和重要度Tab.5 Threshold level and importance of pipes

对供水管网的路径进行分析，共得出 10条路径，依据各路径的组成单元及其重要度，由式(6)计算各路径的重要度，计算结果见表6．

表6 各路径重要度Tab.6 Importance of each path

为求解各路径上的连通率，首先要计算单元正常工作的概率，采用 Sobol序列进行抽样，确定管网中各单元 1,a内发生故障的次数，由式(7)求出各个单元正常工作的概率，再根据各路径上单元组成，代入式(8)求得管网各路径连通率．结合路径重要度和路径连通率，由式(9)计算出整个供水管网系统可靠度．利用 Matlab软件强大的数学计算功能，并基于Visual C＋＋编程语言和 SQL Server数据库实现基于 Sobol序列拟蒙特卡罗法的供水管网可靠度的计算过程，为了与传统蒙特卡罗法计算结果进行对比分析，同时采用伪随机数序列进行供水管网系统可靠度计算，两者求解管网可靠度结果对比、标准差对比结果分别见图5和图6．通过对两者的计算结果进行比较可以看出，进行1,000次抽样模拟后，Sobol序列的模拟结果基本趋于稳定，管网系统可靠度为0.983,889，标准差为 1.497×10-4；伪随机数序列模拟结果仍然存在振荡，标准差相对较大．两者的模拟结果与误差统计见表7．

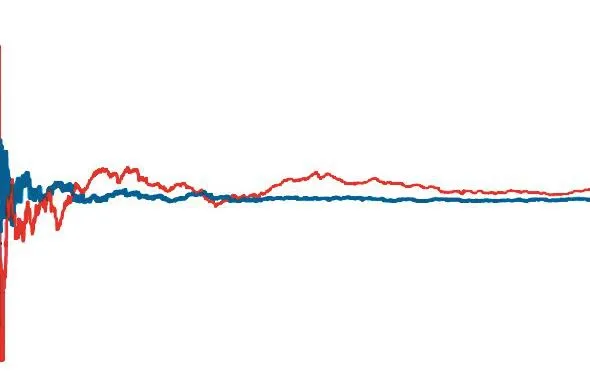
图5 Sobol序列与伪随机数序列求解管网可靠度曲线Fig.5 Reliability solved with Sobol sequence and pseudorandom sequence

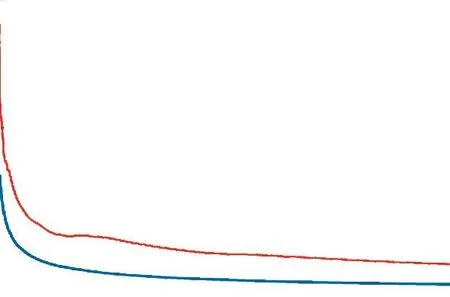
图6 Sobol序列与伪随机数序列求解可靠度标准差曲线Fig.6 Results′ standard deviation solved with Sobol sequence and pseudo-random sequence

表7 模拟计算结果与误差统计Tab.7 Statistics of simulation results and standard deviation

4 结 论

(1) 基于阈级的单元重要度能够对供水管网系统中关键组件进行识别．当单元中的流量越集中时，单元组件故障时阈级越小，该组件对管网系统重要性越大，对管网可靠性的影响程度越高．

(2) 可以通过减小单元的故障率和修复时间提高管网网络系统可靠性，此外，还应尽量避免管段流量过度集中，在条件允许下分散管网管段流量，根据单元的重要度大小采取有层次的维护加固措施．

(3) Sobol序列能保证点列具有更强的均匀性，避免了伪随机数序列的随机性，在进行 1,000次抽样模拟后，伪随机数序列的模拟结果仍然存在振荡，而Sobol序列模拟的系统可靠度为0.983,889，标准差为1.497×10-4，求解结果基本趋于稳定，具有更高精准度和稳定性，收敛时间更短．

(4) 将矿井防尘供水管网路径重要度与连通率相结合，建立了管网系统可靠性计算模型，并采用基于 Sobol序列的拟蒙特卡罗法对管网系统可靠度求解，并将该模型应用于矿山实例，为矿井防尘供水管网系统可靠性分析提供一种新思路．