双曲空间中多值非扩张映射的混合型迭代的强收敛定理
2018-08-02杜保营雷贤才
杜保营, 雷贤才
(宜宾学院 数学学院 四川 宜宾 644000)
1 引言及预备知识
关于不动点理论的研究最近几年有一些新的突破。唐艳,闻道君[1]研究了Banach空间中非扩张半群不动点粘性逼近方法;刘敏[2]研究了广义平衡问题的强收敛定理;雷贤才[3-4]研究了双曲空间中混合型迭代的Δ-收敛定理以及全渐近非扩张映射在CAT(0)空间中的新迭代算法。Markin[5-6]用Hausdorff度量研究了多值收缩以及非扩张映射。之后,又有一些学者[5-21]在Banach空间中,用不同的迭代过程逼近多值非扩张映射的不动点并做了广泛的推广。这类映射的一些有趣而丰富的不动点理论发展起来,并在控制论,最优化,微分方程以及经济学中[7]都有一定的应用。本文将要讨论的问题是:多值非扩张映射的不动点理论。因此,摆在我们面前的是下面这个问题。
问题:在一般的双曲空间中,对于多值非扩张映射,是否可以找到一个迭代方案,使之能够很好地逼近该映射的一个公共的不动点?
在自然科学领域中,大部分的变量关系是非线性关系。而不动点理论是建立在正则的线性空间或者Banach空间中,这些空间主要由它们的线性结构所确定。非线性结构的不动点理论是将一个度量空间嵌入到一个凸集中。双曲空间是非线性的,从几何结构中建立不动点理论是一个很抽象的理论。几何组中一个主要的研究对象就是双曲组,这个问题是在双曲空间的研究中占有统治地位。为了在一般的Banach空间中定义多值非扩张映射,先介绍基本概念。
设E是实Banach空间,K是任意一子集,如果对于任意的x∈e,都存在ν∈K,使
d(x,y)=inf{‖x-ν‖|y∈K}=d(x,K)
成立,则称K是渐近极限集。
由此可知:Banach空间的弱紧凸子集和一致凸Banach空间的闭凸子集都是渐近极限集。以P(K)表示K的非空有界的渐近极限集的子集族,以CB(K)表示K的所有非空有界的闭子集类。设H是由E的度量d诱导的一个Hausdorff度量,即对于任意A,B∈CB(E),都有
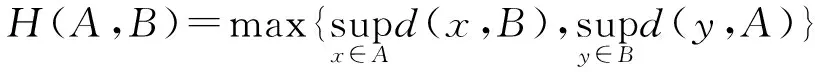
设T是一个多值映射T:K→P(K)如果满足存在k∈[0,1)对于任意x,y∈K,都有
H(Tx,Ty)≤k‖x-Y‖
则T称为压缩的。
定义1.1[19]设T是一个多值映射T:K→P(K),如果满足
H(Tx,Ty)≤k‖x-y‖,∀x,y∈K。
(1)
则T称为非扩张的。
引理1.1[16] 设T是一个多值映射T:K→P(K),Pr(x)={y∈Tx:‖x-y‖=d(x,Tx)},则下面三个命题是等价的:
(1)x∈F(T)
(2)Pr(x)=x
(3)x∈F(Pr),而且F(T)=F(Pr)
Kohlenbach[22]介绍了双曲空间,本文的工作在双曲空间中开展,下面的定义在文献[23]中有介绍,但在双曲空间中有局限性,所以这些定义要比在双曲空间中更具有一般性。
设双曲空间X是一个度量空间(X,d),W是一个映射W:X2×[0,1]→X且满足∀x,y,z,w∈X,α,β∈[0,1]
(1)d(u,W(x,y,α))≤αd(u,x)+(1-α)d(u,y);
(2)d(W(x,y,α),W(x,y,β))=|α-β|d(x,y);
(3)W(x,y,α)=W(y,x,1-α);
(4)d(W(x,z,α),W(y,W,α))≤(1-α)d(x,y)+αd(z,w)。
设E是双曲空间X的一个非空子集,如果对于∀x,y∈E,α∈[0,1]都有W(x,y,α)∈E,则E是凸的。双曲空间族包含赋范空间和它的一个凸子集。Hadamard[25]在Hilbert球中建立了双曲度量,Gromov[26]在很多CAT(0)空间中也做了相应的研究。
在一个双曲空间中,对于任意r>0,ε∈(0,2],存在δ∈(0,1],使对于所有的u,x,y∈X若d(x,u)≤r,d(y,u)≤r,d(x,y)≥εδ,都有

则该双曲空间是一致凸的。
对于给定的r>0,ε∈(0,2],定义映射δ=η(r,ε);(0,+∞)×(0,2]→(0,1],可以看做X上的的一致凸性模。
最后,设(X,d)是一个度量空间,K是X的一个非空子集,我们以F(T)来T表示的不动点集,即F(T)={x∈K:Tx=x}。设T是映射T:K→K,如果满足:对于∀x,y∈K,
d(Tx,Ty)≤d(x,y)
则T称为非扩张的。
设T是映射T:K→K,如果存在序列{kn}⊂[0,+∞),且kn→0,都有
d(Tnx,Tny)≤(1+kn)d(x,y),∀x,y∈K。
则T称为渐近非扩张的。
设T是映射T:K→K,如果存在一个常数L>0$L>0$,对于∀x,y∈K。都有
d(Tnx,Tny)≤Ld(x,y)。
则T称为一致L-Lipschitzian。
本文目的是在Banach空间中将一个多值非扩张映射的迭代方案推广到双曲空间中,并证明一个强收敛定理:即用混合迭代过程逼近两个多值非扩张映射以及两个渐近非扩张映射的一个不动点。在双曲空间中,还可以推广并改变其他领域的一些成果文献[10-13,15-17,19,20,25,28]。
为了在双曲空间中定义Δ-收敛,首先介绍一些基本概念和引理。
引理1.2[30] 设(X,d,W)是完备一致凸的双曲空间,且它的有单调的一致凸性模。则X中的每一个有界序列{xn},对于X的每一个非空闭凸子集K而言有唯一的一个渐近中心。
由分析知识可知:设x∈X,xn是X中的序列,如果对于{xn}中的任何子序列{un},都有x是{un}的唯一渐近中心,则称{xn}收敛到x,记为Δ-limn→∞xn=x,并称x是{xn}的Δ-极限。
一个映射T:K→K,对于任何一个有界序列{xn}⊂K,如果d(xn,Txn)→0,那么{xn}有一个收敛的子序列,则称为半紧的。
引理1.3[31] 设是an,bn,δn非负是数列,并且满足:
an+1≤(1+δ)an+bn,∀n≥1
(2)




2 主要结果

(3)
其中μn∈SS1yn,νn∈SS2xn,d(νn,μn)≤H(SS2xn,SS1yn)+τn,{τn},{αn},{βn}满足下列条件:

(3)‖xn-p‖=d(xn,p),‖yn-p‖=d(yn,p);
(4)d(x,Tiy)≤d(SSix,Tiy),∀x,y∈K,i=1,2。
如果SS1,SS2,T1,T2中有一个是半紧的,则如上所定义的序列{xn}(在度量拓扑中i.e.)强收敛到一个不动点p∈B。

第一步:首先证明:对于∀p∈B极限limn→∞d(xn,p)存在。
对于∀p∈B,因为SS1,SS2是一个多值非扩张映射,T1,T2是一个渐近非扩张映射,由条件(2),(3)可得




≤(1-αn)d(xn,p)+αn(1+kn)H(SS1yn,SS1p)+(1+kn)αnτn
≤(1-αn)d(xn,p)+αn(1+kn)‖yn-p‖+(1+kn)αnτn
≤(1-αn)d(xn,p)+αn(1+kn)d(yn,p)+(1+kn)αnτn
(4)
其中




≤(1-βn)d(xn,p)+βn(1+kn)H(SS2xn,SS2p)+(1+kn)βnτn
≤(1-βn)d(xn,p)+βn(1+kn)‖xn-p‖+(1+kn)βnτn
=(1-βn)d(xn,p)+βn(1+kn)d(xn,p)+(1+kn)βnτn
(5)
=(1+βnkn)d(xn,p)+(1+kn)βnτn
所以
d(xn+1,p) ≤[1+αn(1+βn+βnkn)kn]d(xn,p)
+[1+(1+kn)βn](1+kn)αnτn
(6)

第二步:证明对于∀p∈B
(7)
由第一步可知:极限limn→∞d(xn,p)存在,不妨设limn→∞d(xn,p)=c≥0如果c=0,则结论显然成立。下面考察c>0的情况。由(5)可知:
d(yn,p)≤(1+βnkn)d(xn,p)+(1+kn)βnτn
(8)
对上式两边同取极限可得:

(9)
另外因为

所以

(10)
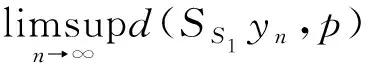
(11)

(12)
由(10)-(12)及引理1.4可得
(13)
同样的方法可得
(14)
根据条件(4),由(13),(14)可得

(15)
以及

(16)
由(3),(14)可得
(17)
以及
(18)
注意到
由(16),(17)可得
(19)
又由(15)可得
(20)
另一方面,由(13),(19)可得


(21)
因此,由(20),(21)可得

(22)
另外,因为

以及(15),(22)可得
(23)
综上,可得对于i=1,2都有下式成立


由(16),(20),(23)可得
(24)
因为

由(14),(16),(20),(21)可得
(25)

事实上,因为对于∀p∈F极限limn→∞d(xn,p)存在,所以序列limn→∞d(xn,p)是有界的。因此由引理1.2可知序列{xn}有唯一一个渐近中A({xn})=xn。设{μn}是{xn}的任何一个子序列,记A({μn})={μ}由(7)可知下式成立
(26)



(27)
因为Ti满足一致L-Lipschitzian,由(27)可得
d(zj,μn)≤(1+kn)d(μ,μn)+jLd(Tiμn,μn)。
对上式两边同取上极限,并由(26)可得

因此
r(zj,{μn})≤r(y,{μn}),∀y∈K⊂X。
所以

故

第四步。证明limn→∞d(xn,p)=0。
利用(24),(25)以及SS1,SS2,T1,T2中有一个是半紧的,可知{xn}存在的一个子序列{xni}⊂{xn}强收敛到p∈K。而且由SS1,SS2,T1,T2的连续性可知:对于任意i=1,2有下面两式成立
即p∈B。又由第一步:极限limn→∞d(xn,p),p∈B存在。所以limn→∞d(xn,p)=0。定理证毕。

(28)
其中νn∈SS2xn,μn∈SS1yn,d(νn,μn)≤H(SS2xn,SS1yn)+τn,{τn},{αn},{βn}满足下列条件:

(3)‖xn-p‖=d(xn,p),‖yn-p‖=d(yn,p);
(4)d(x,Tiy)≤d(SSix,Tiy),∀x,y∈K,i=1,2。
如果SS1,SS2,T,T2中有一个是半紧的,则(28)所定义的序列{xn}(在度量拓扑中i.e.)强收敛到一个不动点p∈B。
证明:在(3)中令Ti=I,i=1,2。因为满足定理2.1中所有的条件,所以由定理2.1可得序列{xn}强收敛到B中的一个公共不动点。定理证毕。
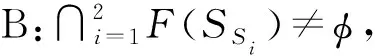
(29)
其中νn∈SS2xn,μn∈SS1yn,d(νn,μn)≤H(SS1xn,SS2yn)+τn,{τn},{αn},{βn}满足下列条件:

(3)‖xn-p‖=d(xn,p),‖yn-p‖=d(yn,p)。
如果SS1,SS2中有一个是半紧的,则(29)所定义的序列{xn}(在度量拓扑中i.e.)强收敛到一个不动点p∈B。
证明:在(28)中令Ti=I,i=1,2。因为满足定理2.1中所有的条件,所以由定理2.2可得序列{xn}强收敛到B中的一个公共不动点。定理证毕。

(30)
其中νn∈SS2xn,μn∈SS1yn,d(νn,μn)≤H(SS2xn,SS1yn)+τn,{τn},{αn},{βn}满足下列条件:

(3)‖xn-p‖=d(xn,p),‖yn-p‖=d(yn,p);
(4)d(x,Tiy)≤d(SSix,Tiy),∀x,y∈K,i=1,2。
如果SS1,SS2,T,T2中有一个是半紧的,则(30)所定义的序列{xn}(在度量拓扑中i.e.)强收敛到一个不动点p∈B。
证明:在(3)中令SSi=I,i=1,2。因为满足定理2.1中所有的条件,所以由定理2.1可得序列{xn}强收敛到B中的一个公共不动点。定理证毕。
