任意强度磁场中氦原子能级的塞曼分裂
2018-08-02朱志海黄时中
朱志海, 黄时中
(安徽师范大学 物理与电子信息学院,安徽 芜湖 241000)
引 言
探索原子和分子在强磁场等极端条件下的行为,是揭示新物理现象的重要途径之一。在这类研究工作中,原子在强磁场中的能级结构是一个关键性的基础问题[1-6],因而一直备受关注。就较为简单的氢原子和氦原子而言,已报导了很多研究工作。例如,对于氢原子,2009年Thirumalai等[6]通过求解H-F微分方程,在柱坐标系中计算了不同强度的磁场中氢原子的几个低能级的理论值;2010年张昌莘等[7]采用简并态微扰论分析了在中等磁场中氢原子的能级结构特征;2011年褚进民等[8]借助角动量耦合理论导出了中等磁场中氢原子n=5能级的塞曼分裂的表达式;2011年曾思良等[9]采用非微扰论讨论了强磁场中氢原子能级结构的特点。对于氦原子,目前的研究工作还是以弱场情形下的线性塞曼效应为主,代表性的工作有:1970年Lewis等[10]导出了弱场情形下氦原子塞曼哈密顿的完整形式,不仅包含了通常的自旋和轨道角动量与外磁场的相互作用,还考虑到了原子核的运动、辐射修正、相对论修正;1973年Schiff等[11]给出了较准确的3p态精细结构裂距;1978年Kramer等[12]利用交叉光谱学技术测定了氦原子33p态的精细结构裂距;2000年黄时中等[13]在考虑各种相对论修正、核运动修正和辐射修正的基础上,采用微扰与变分相结合的方法,导出了氦原子23p态线性塞曼效应的解析解;2005年Hansen等[14]测定了钙原子高激发态的朗德g因子;2006年孙云等[15]利用不可约张量理论导出了氦原子1snp组态线性塞曼哈密顿矩阵元的一般形式,导出了氦原子1s3p组态线性塞曼效应之解。最近,朱志海等[1]借助角动量耦合理论以及不可约张量理论,成功地导出了任意强度磁场中氦原子1snp组态(其中n≥2)的平方塞曼分裂能级的解析表达式。进一步的研究发现,此方法可以推广到氦原子的所有里德堡态(组态为1snl,其中n和l可取一切可能值),更一般地导出氦原子在任意强度磁场中各里德堡态的塞曼分裂能级的解析表达式,其中既考虑了线性塞曼效应又考虑了平方塞曼效应。本文报道这一推广工作,为进一步研究强磁场中氦原子之间的相互作用色散系数[16]等问题奠定必要的理论基础。
1 氦原子塞曼效应哈密顿本征方程的近似解
(1)
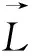
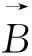
(2)
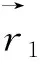
(3)
此处B0是磁感强度的常用原子单位。
在一级近似下,塞曼哈密顿Hz对氦原子精细结构能级E(0)(LSJ)的修正值为
Ez(LSJ)=〈LSJMJ|Hz|LSJMJ〉
(4)
其中|LSJMJ〉是氦原子精细结构能级E(0)(LSJ)的波函数,可以表示为
(5)
此处〈LSMLMS|LSJMJ〉表示C.G.系数;|LSMLMS〉表示氦原子的拉卡波函数,其具体的解析表达式见文献[18]。
以式(4)和式(5)为基础,借助不可约张量理论[17],可以导出式(4)中的对角矩阵元的解析表达式,得到氦原子各里德堡态(电子组态为1snl,其中n和l可取一切可能值)的塞曼分裂能级的如下表达式:
(6)
此处
(7a)
其中
(7b)
而
(8a)
其中
(8b)
式中的径向函数Rnl(r)的具体形式是
(9)
(10)
此处ηnl是采用变分方法计算非相对论性哈密顿HNR的本征值ENR(LS)的过程中所得到的变分参数。
2 任意强度磁场中氦原子能级的塞曼效应
利用上述结论,可以分析氦原子所有里德堡态(组态为1snl,其中n和l可取一切可能值)的塞曼效应,具体方法和主要结论如下。
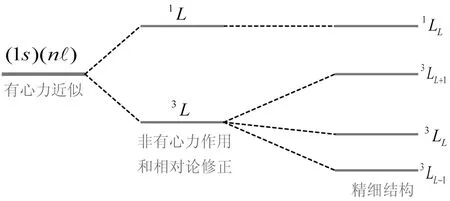
图1 氦原子(1snl)组态的精细结构能级示意图
氦原子(1snl)组态的精细结构如图1所示,按照(7b)式,可以得到精细结构能级1LL、3LL+1、3LL、3LL-1的gLSJ值依次为
g(1LL)=1
(11a)
(11b)
(11c)
(11d)
按照(7a)式,氦原子(1snl)组态的精细结构的线性(γ的一次项)塞曼分裂的具体表达式为
(12a)
(12b)
(12c)
(12d)
下面应用(8)式,进一步分析氦原子的(1snl)组态的精细结构能级1LL、3LL+1、3LL、3LL-1的平方(γ的二次项)塞曼效应。先分析精细结构能级1LL的平方塞曼效应,按照(8a)式,有
(13)
利用式(9)和(10)计算出上式中的径向因子G(1snl,1L),得到
(14)
将式(14)代入式(13)得到
(15)
依据MJ=L,L-1,…,-L计算出式(15)中的3j符号之值,可以得到
(16a)
(16b)
⋮
(16c)
综合以上各式,我们得到精细结构能级1LL的塞曼效应的如下表达式
(MJ=L,L-1,L-2,…,-L)
(17)
类似地分析精细结构能级3LL+1、3LL、3LL-1的塞曼效应,可以进一步得到
(MJ=L+1,L,L-1,…,-L-1)
(18)
(MJ=L,L-1,L-2,…,-L)
(19)
(MJ=L-1,L-2,L-3,…,-L+1)
(20)
3 任意强度磁场中氦原子里德堡态塞曼效应的分裂结构图
任意强度磁场中氦原子里德堡态塞曼效应的上述结论较为复杂,为了能够直观地显示氦原子里德堡态塞曼效应的特征,我们利用Mathematica软件绘出了任意强度磁场中氦原子里德堡态塞曼效应的分裂结构图。为了突出平方塞曼效应的特征,在每个图中既绘出了线性效应(虚线)的分裂结构图,又绘出了线性效应与平方效应合成后(实线)的分裂结构图。以氦原子(1s2p)组态的塞曼效应为例,塞曼效应的分裂结构图如图2至图5所示。
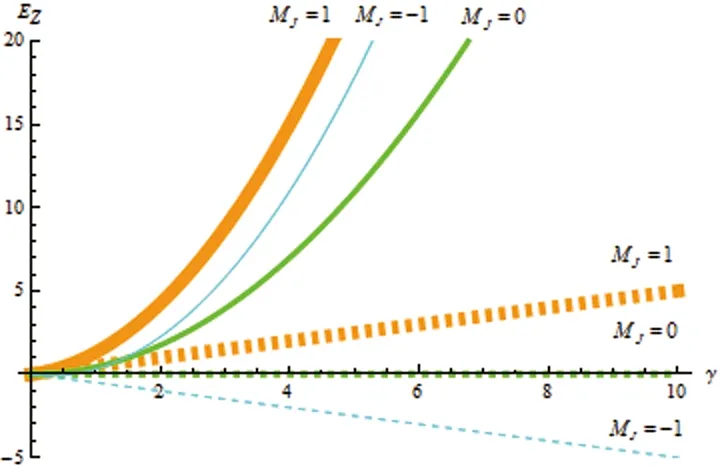
图2 氦原子(1s2p)组态精细结构能级1P1的塞曼分裂能级图
图3 氦原子(1s2p)组态精细结构能级3P2的塞曼分裂能级图
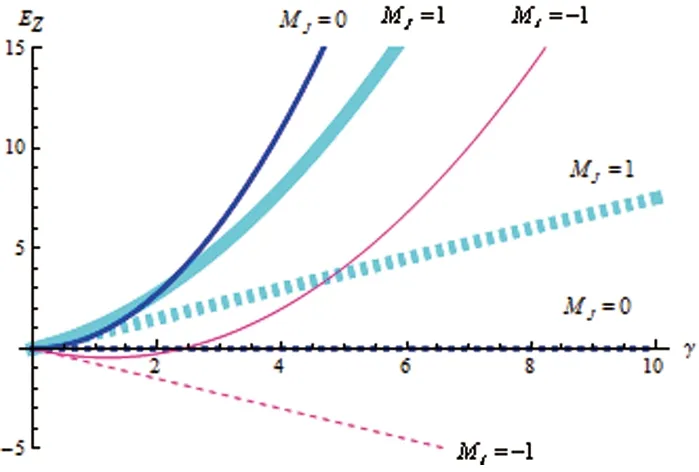
图4 氦原子(1s2p)组态精细结构能级3P1的塞曼分裂能级图
图5 氦原子(1s2p)组态精细结构能级3P0的塞曼分裂能级图
按照上述任意强度磁场中氦原子里德堡态塞曼效应的分裂结构图,可以得到下述基本结论:
(1)MJ=0的能级存在移动效应,且
能级1P10和3P20向下移动;能级3P10和3P00向上移动。
(2)能级裂距不再均匀(非线性效应),且
能级1P1,1向上移动,远离能级1P10;能级1P1,-1向上移动,靠近能级1P10;
能级3P2,2向上移动,远离能级3P20;能级3P2,-2向上移动,靠近能级3P20;
能级3P1,1向下移动,靠近能级3P10;能级3P1,-1向下移动,远离能级3P10。
任意强磁磁场中氦原子里德堡态塞曼效应的这些特征,为进一步研究强磁场中氦原子之间的相互作用色散系数等问题奠定了必要的理论基础。
