一种基于单幅图像的主平面检测算法

赵晓莹，刘艳丽

（1.四川大学计算机学院，成都 610065；2.四川大学视觉合成图形图像国家重点实验室，成都 610065）

0 引言

在真实的自然环境中，存在着丰富的平面结构信息，尤其是在建筑物场景中。在透视投影下，物理世界中的平面在不同视点下的图像可通过单应性相互关联。由于平面这种特殊的几何性质，平面检测被广泛应用于图像拼接、障碍物检测、三维重建、场景分析及增强现实等领域中。

目前，在计算机视觉领域，已出现了一些平面检测算法，但这些平面检测算法都是基于两张图像间的对应关系。到目前为止，平面检测都是以标识平面中的特征点[1]或部分区域[2-3]作为最终结果，而本文提出的平面检测算法则标识完整的平面区域。

1 相关工作

常见的平面检测算法是类似随机抽样一致性（Random Sample Consensus，RANSAC）方法[4-6]，假设一个初始样本模型，选择原始数据中的一组特征点计算单应性矩阵作为初始样本模型，通过反复迭代测试，得到最优的数据模型参数，但是该算法的精确度及鲁棒性很大程度上依赖于匹配准确度。Toldo等人[7]提出了一种基于随机抽样和概念数据表示的聚类算法J-link⁃age，用于将模型的多个实例拟合成受噪声和异常值影响的数据，每个点用其偏好集的特征函数表示，多个模型在概念空间中显示为群集。该方法不需要事先规定模型的数量，也不需要参数调整，在多平面检测中有很好的应用。曹芳等人[8]提出一种基于匹配点相似度引导采样的分层多平面检测算法，利用残差信息的排序和加权分析选择匹配的特征点采样，将属于同一平面结构的匹配特征点加入采样集合，提高了采样点集合的全内点概率，可快速得到最优单应性矩阵的参数模型。

上述算法都是基于两张或多张图像特征点匹配而检测的平面。不同于传统的平面检测算法，本文提出了一种新颖的单张图像平面检测算法，利用Mean Shift图像分割划分平面区域后，结合消失点分类线段约束平面边界从而检测完整的平面区域。

2 算法实现

如图1所示本文的算法流程主要分为三个部分，

图1 算法流程图

第一部分线段分类，通过检测图像中的线段得到图像中的三个消失点。利用消失点将图像检测到的线段进行分类，每一类线段在世界坐标系中相互平行。由于建筑物平面由两对平行线相交得到，因此对于完整平面区域的检测可以通过当前平面最外围相互平行的两对平行线来确定。

第二部分图像分割，在已分类的线段中，由于窗户边缘以及平面外其他物体边缘等干扰物对于线段造成误判，使得无法通过两组平行线来确定平面边界。利用图像分割对图像像素值相似区域进行分割，对于部分区域中的干扰通过像素替换法去除干扰。

第三部分图像去噪，对于图像分割后的图像通过检测两组平行线交点来确定主平面颜色，找到图像主颜色最大的平面区域，利用周边相互平行的两组平行线段确定该区域边界，对于平面下边界的一些干扰，如地面阴影、草地等，通过图像去噪的方法消除干扰。

2.1 线段分类

Li等人[9]通过在图像中线段交点的角度坐标直方图中寻找峰值的方法获得消失点的角度坐标，进而求得消失点坐标。消失点要满足公式（1），其中点（x1,y1），（x2,y2），（x3,y3）分别代表三个消失点，f为焦距。

消失点确定后将图像中的线段Li（i=0,1,2,3...）分类，直线表达式和距离条件表达式如公式（2）。通过消失点（xj,yj）到直线Li的距离dij满足一定阈值a，判断线段Li属于消失点类Dj，本文中a的阈值设为30。若不存在消失点（xj,yj）到直线Li距离满足阈值a，则抛弃线段Li。当线段Li同时属于两个消失点类时，分别在这两个消失点类中随机选取两条线段作为候选线段，计算候选线段与线段Li交点，若两个交点都在当前候选线段所在类的消失点附近，则判断线段Li属于当前消失点类。分类结果如图2所示，三组不同的消失点分别用红绿蓝颜色标识。在该例子中我们检测的主平面区域是选取蓝色和绿色标识的两组平行线段相交而得。

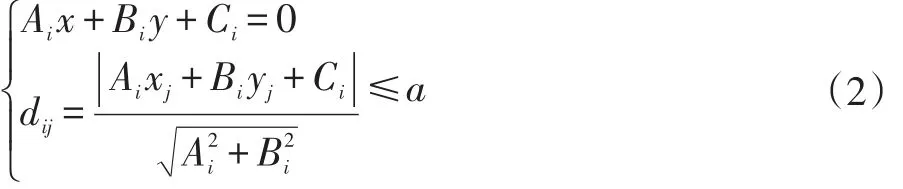
图2 线段分类结果

2.2 图像分割

图像分割，是将灰度图或彩色图像分解成同质图像块，同质性在像素值中通常被定义为相似性，即在图像上执行分段常数模型。Comaniciu等人[10]采用感知色差对应颜色特征空间的欧几里德距离思想，即一种新的感知均匀的颜色空间度量算法进行平面分割。

上述思想分割图像后存在许多小块区域，例如建筑物一个平面中的小窗户仍是独立存在的一个分割结果，如图3（a）。但我们的平面检测结果，窗户是属于当前平面的一部分，所以需要与周边大块分割结果融合。以像素坐标为单位，当小块区域像素个数低于某一阈值，则查找周边其他块像素个数，若足够大，则将小块区域像素值（RGB）替换成周边大块区域像素值。最终分割结果如图3（b）所示。

图3

2.3 图像去噪

图2 中，我们计算蓝色和绿色标识的两组平行线段交点，在这里需要对每条线段设置一个标志位，当遇到同类线段时不计算交点。利用这些交点的像素值计算主平面的颜色，像素值是主平面颜色的交点被保留下来计算凸包。我们将这些凸包外围点分成四类，分别是上下左右四个方向，并且计算左上左下右上右下的四个顶点，左上顶点既属于左方向又属于上方向，其他三个顶点类似。在所有线段中选择离左方向上的点最近的线段作为平面左边界线段，其他三条线段都依此选择，从而初步检测到平面区域边界线段，如图4（a）。我们通过验证当前线段过主平面的点个数比率来判断检测的平面边界是否偏离真实平面边界，若过主平面的点比率较小时排除该线段，重新计算离当前方向上的点最近的线段作为边界线段。

但是由于平面下边界即与地面相连的边界线段有诸多干扰，如草地、阴影及遮挡等都会造成干扰使其检测的边界线段不准确，我们针对下边界做额外的优化使准确检测平面下边界。在这里我们需要用到绝对二次曲线原理公式（3），d1，d2是两条直线方向（三维矢量），x1，x2分别为 d1，d2方向上的两个点，K 为相机内参矩阵，由焦距f构成的上三角矩阵，在欧式世界系中这两条直线方向夹角为cosθ。由此我们推出公式（4），V1，V2为两个消失点，而两个消失点在欧氏世界系中的方向夹角为90度，即cosθ=0。由2.1计算的消失点存在误差，而我们已有准确的上左右三个方向线段，消失点V1可由左右方向线段交点而得，公式（3）中的焦距f已由2.1小节计算，且已知V2过上方向线段，则根据公式（3）计算V2。因此我们计算离下方向上的点较近的一组候选线段，使上方向线段分别与候选线段计算交点，选择离消失点V2最近的交点，则下方向线段被确定出来。完整的平面区域结果如图4（b）所示。

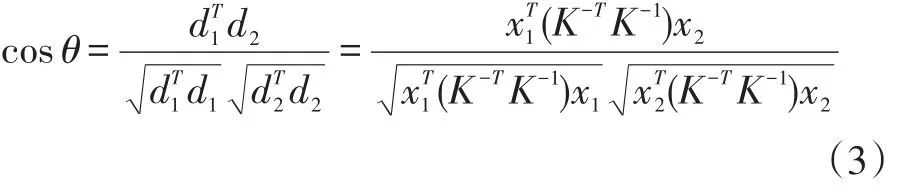
3 实验结果

通过对本文算法与RANSAC算法检测平面结果进行比较，运行结果如图5所示。图5（a）是通过标识特征点检测平面，但偶有异常点出现是不可避免的；图5（b）是尽可能排除异常点后由凸包画出检测的平面特征点；图5（c）是本文算法检测的平面。结果表明，利用图像分割结果与消失点分类线段算法检测到的平面区域更准确。

4 结语

在平面结构较为简单的建筑物场景中，本文提出的利用Mean Shift图像分割划分平面区域后，结合消失点分类线段约束平面边界的平面检测算法有效且准确检测完整的平面区域，为后续平面跟踪及检测新平面出现提供信息和帮助。但该算法受限于条件设置，若场景中干扰物较多，存在干扰线段使得线段分类不准确，平面检测结果则会不理想，这是下一步要解决的重点问题。

图4

图5