基于双因子的综合布线测试实验室能力比对判定方法研究
2018-08-01陈奂昊刘烨相里朋
陈奂昊,刘烨,相里朋
(工业和信息化部电子第五研究所,广州 510610)
1 综合布线测试比对测试
实验室比对测试是实验室间常用的能力维持手段,根据ISO17043:2010及GB/T 27043-2012的要求实验室间进行比对测试可以有以下目的:评定实验室从事相关检测的持续能力,识别实验室存在的问题并加以改进,建立检测方法的有效性和可比性,识别实验室的差异,相互学习提高检测能力等[1]。综合布线第三方检测是在综合布线建设中较重要的环节,为建设方完成工程验收提供验收依据。第三方实验室需要不断保持和改进检测能力以确保工程验收的客观性和准确性。各实验室定期组织开展比对测试有利于行业内的交流,保持各实验室检测能力的一致。
2 统计方法及判定
比对测试使用的检测工具经过正规校准,但是检测工具具有差异性和不确定性,例如新国标把光纤测试所需要的LED光源修改为EF光源,EF光源尽管比LED具有更高的精度但仍存在10%的波动性[2],另外人员操作方法不相同,对设备的保养水平也不同,测量结果会具有一定的差异,例如光纤测试中,光纤端面的清洁不足,可令一颗10mm的灰尘将9mm的光纤造成衰减大增[3]。假定各实验室的检测水平已取得CNAS认可,需要判定各单位测量结果是否一致或存在偏差,数学统计方法是公认合理的判定方法。
2.1 常用统计方法
行业进行比对测试常用的统计方法[4]有算术平均数、标准差、中位值、四分位距、变异系数等。详见表1。
从表1的分析来看,各统计方法适用于不同的范围,以上分析是假定测量值服从于正态分布。
2.2 统计方法分析
奈曼-皮尔逊为数值统计定义了两类风险,即α风险和β风险,或者称为第I类错误(风险)和第II类错误(风险),第I类错误是产生弃真,第II类错误则产生取伪,所以单一的统计判定方法容易导致风险。
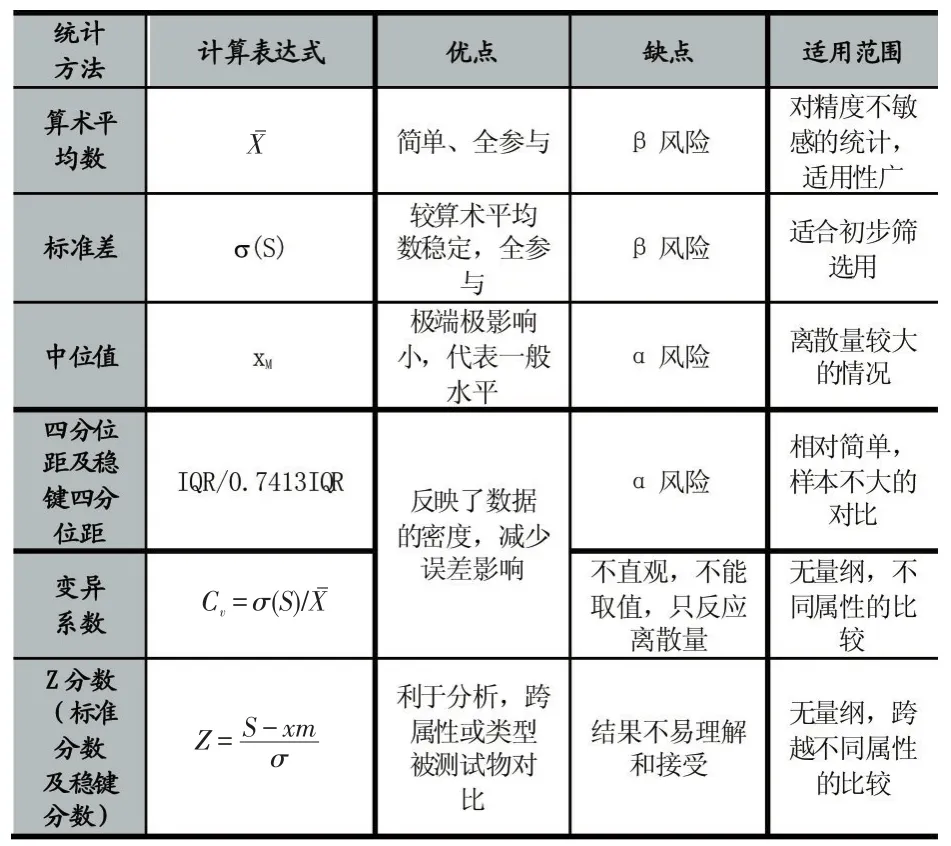
表1 常见统计分析方法及优缺点分析
在实际比对验证中,为了进一步分析和降低风险,考虑宜采用多种统计方法结合的综合统计。选用单个统计方法我们称为单因子分析方法,取用多种统计方法则称为多因子分析方法。
单因子分析方法优势是快速、简单,易于理解和接受,但易导致风险。另外多因子分析方法计算复杂,随着因子增加,正确的结果也有可能被大量的排除,但多因子可减少风险,评价结果可信度相对较高。
经上述分析,可确定选择判定方法的原则:比对样本越少越宜于使用单因子分析法,反之宜采用多因子分析法,但是又应该要避免使用的因子过多。
本次对比测试参数较多,但测量值较少,考虑需要中和α风险和β风险,四分位距法(β风险)与最大差值法(一组测量值中,筛选出与均值差值最大的测量值,α风险)联和采用则可满足这要求。

上式是本次比对测试对测量值进行判定的基本算式。E:单项性能比对时“离群”值结果,取两种分析方法结果的交集,D1和D2表示为通过两种分析方法来确认该值是否“离群”。
为验证本次测试结论的有效性,从表1中可选择低风险的方法进行对照验证。变异系数和Z分数(含标准Z分数和稳健Z分数)是理想的参照方法。
2.3 判定方法
上节分析了对单个测量值的单个参数利用多因子分析方法进行统计和评价,综合布线测试结果有多参数需要比对同时还要作整体性评价,整体性评价的作用是确认该项测试整体是否满意或离群。结合上一节的分析结果,下节给出判定的方法。
(1)单项结果评价原则
收集所有实验室的测量结果横向比较,采用四分位距法和最大差值法对测量结果对测量项进行双因子综合评价,当四分位距法和最大差值法的结果不同时出现离群,则测试结果是满意的,否则为离群。
四分位距法的判定公式为:

其中di为第i个实验室某个参数的测定值,d为所有参与实验室某个参数的均值,IQR代表所有参与实验室所测该参数得到的四分位距(一种统计方法,它是一组数列中上四分位数Q3与下四分位数Q1的差,即IQR=Q3-Q1,该值的计算过程本文不再讨论)。
若Di≤IQR(该参数的四分位值)则记为Δ'i=0否则记为Δ'i=1。 (判定准则1)
最大差值判定式为:
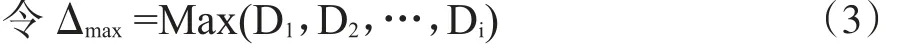
Δmax表示为最大差值。
若 Di< Δmax,则记为Δ''i=0,若 Di=Δmax并且唯一,则记为Δ''i=1,不唯一,则记为Δ''i=0。(判定准则2)
依据(1)式定义,可以得到以下计算式:

Δi是判定式1和判定式2的“离群”值与计算结果;当结果为0时表示“满意”,结果为1时表示“离群”。
图1表示双因子分析方法的取值范围关系示意,为了方便理解,采用了平面图的形式。
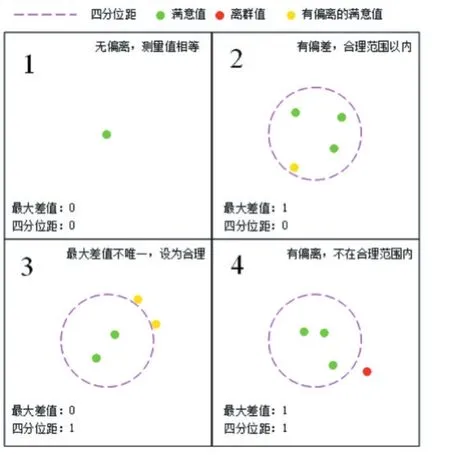
图1 双因子取值范围关系示意图
上图中,假设有四个测量值进行比较(不考虑图中的相位关系),利用判定准则1的结果,虚线内表示这四个值的四分位距合理范围,最大差值法的计算结果可能性有:
图1.1:四个值均为0即相等,结果为满意。
图1.2:出现1个最大值且在四分位距范围以内,结果为满意。
图1.3:出现有2个值在四分位距范围外且相等,则很有可能是正确值,所以保留并认为是满意的。
图1.4:出现1个最大值且在四分位距范围以外,结果为离群。
以上是判定准则2的说明。
(2)整体判定
整体测试结果判定式为:

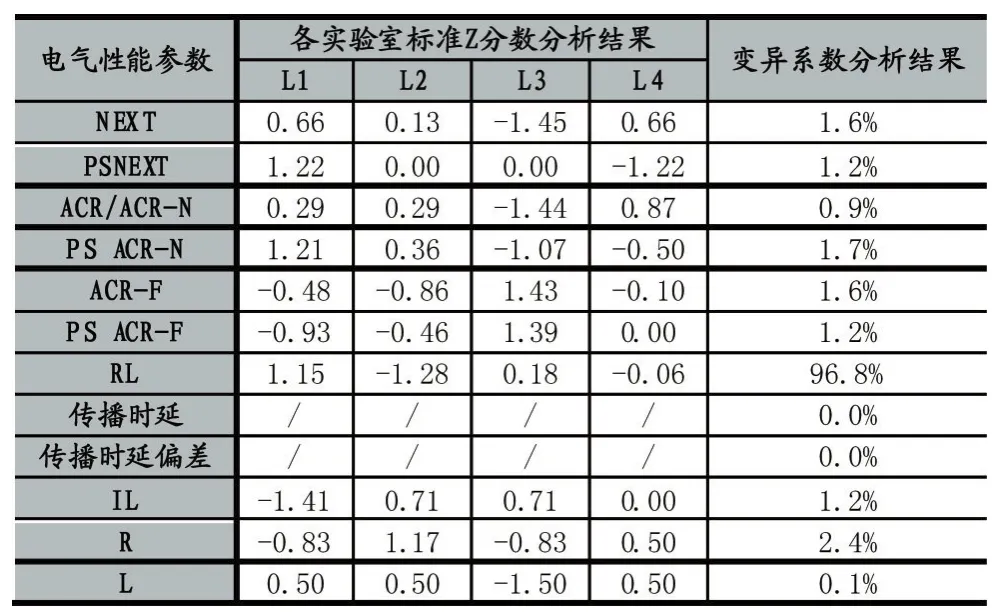
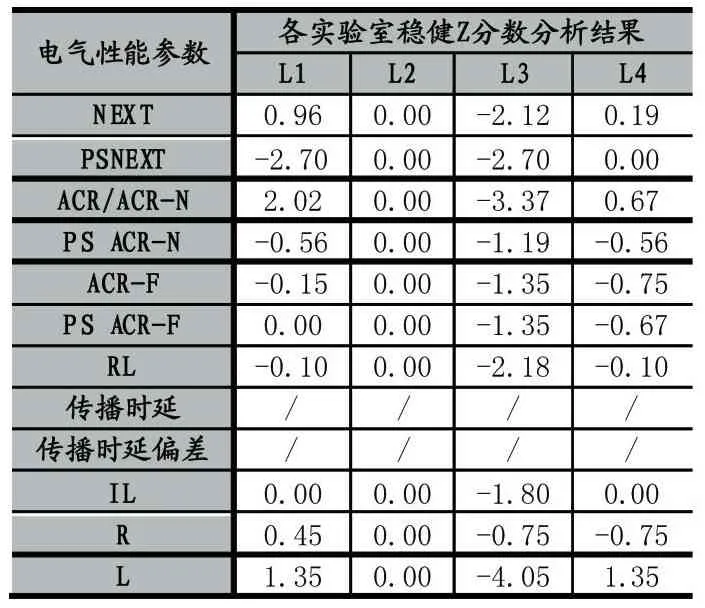
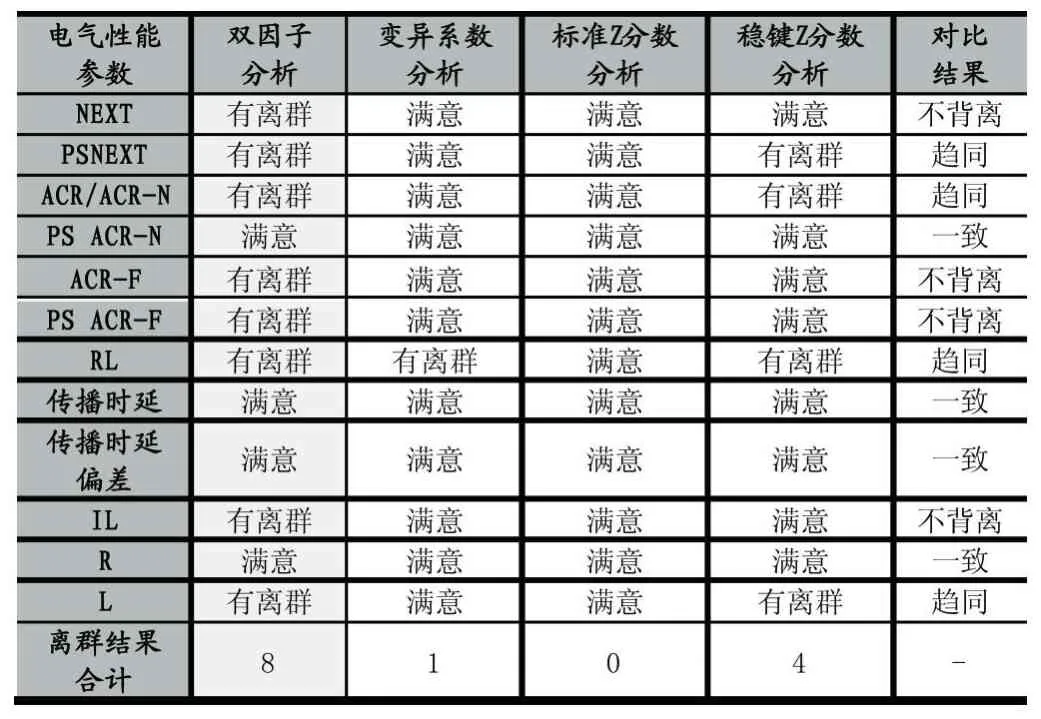
Si:离群判定值,Ri:所有为离群的单项结果;s:判定系数(由各实验室或相关主管单位、行业机构、利益方确定),0 根据前文讨论的采用双因子分析方法,本次参加比对的实验室有四家(即 L1、L2、L3、L4),在完成测试后,将各实验室的测试数据进行统计,下表是统计结果。 表2数据举例说明:NEXT测量值分别为L1=12.2、L2=12.1、L3=12.2、L4=11.8,则平均值为 12.08,IQR=0.175。 根据判定准则 1:Δ1=|d1– d|=0.12,则Δ1<0.175,即Δ'1=0,同理Δ2=0.02,Δ3=0.12,Δ4=0.28,则Δ'2=0、Δ'3=0、Δ'4=1。 根据判定准则 2:Δmax=Max(di-d),Δmax=Δ4=0.28,同时Δ4>IQR,所以Δ''1=0、Δ''2=0、Δ''3=0、Δ''4=1。 表2 双因子及变异系数统计结果 Δ1=0,Δ2=0,Δ3=0,Δ4=1,则 L1、L2、L3 的 NEXT 测量值结果均为满意,而L4的NEXT测量值则判为离群。 全部测量值的综合评价结果(整体评价)详见表3。 经以上各单项评价结果进行综合分析可知,Si=12(i=1,2,3,4),SΔ1=2,SΔ2=1,SΔ3=0,SΔ4=5,分析 s值,L3 实验室结果最好,L4实验室结果最差,s值可按判定准则3中给定。 (1)Z分数的统计公式为: 表3 综合评价结果 S 为测量值;Xm为均值;S-Xm为离均差;s(S)为标准偏差(稳健分数则取0.7413IQR)[4]。 当︱Z︱≤2时,可判断为不偏离。2<︱Z︱<3,则存在问题,︱Z︱≥3则不满意[4]。 (2)变异系数的统计公式为: s(S):可取标准偏差或者稳键四分位距;Xˉ:平均值。Cv值取不大于15%时,认为比对测量值正常。 在进行对比分析前,定义双因子分析与单因子分析结果的趋同原则,当无直接引用的单因子统计方法(本次采用的双因子未引用变异系数和Z分数的分析方法)对同一参数评价时,应要满足的原则是:任一个单因子分析结果为离群时,双因子分析对该参数的评价结论也必然为离群;单因子分析结果为满意时,双因子分析结果不作要求(即可以满意也可以离群)。符合这一原则就是一致(各对比结果完全相同)的或者是趋同(至少一个单因子结果与双因子结果相同)的,至少是不背离的,否则是背离(任一单因子结果出现离群,而双因子结果却为满意)。 表4 标准Z分数和变异系数分析结果 表5 稳键Z分数分析结果 将双因子分析、变异系数评价和Z分数评价(即标准和稳键Z分数)分析结果进行对比,见表6。 表6 分析结果对比验证 变异系数、标准Z分数和稳键Z分数均视为参照对比的单因子统计评价,通过上表“对比结果”列的分析结果可知双因子分析的结果未出现与这些统计分析方法得出的分析结果是背离的,因此可认为,双因子分析的整体结果不背离参照对比的单因子分析整体结果,双因子分析结果显示更为严苛,更能反映出测量结果的细小差异。 比对测试使用同一套测试样本独立进行测试,对于检测结果我们通过双因子分析、变异系数评价和Z分数评价(包含标准和稳键Z分数评价)进行参照对比,发现双因子判定方法较为严格并且不背离传统的统计方法,因而是可采用的有效的判定方法,适合于更为严格的比对要求。双因子的统计和判定方法可以为综合布线性能比对测试的比对判定提供有价值的参考。
3 实例分析
3.1 双因子分析法
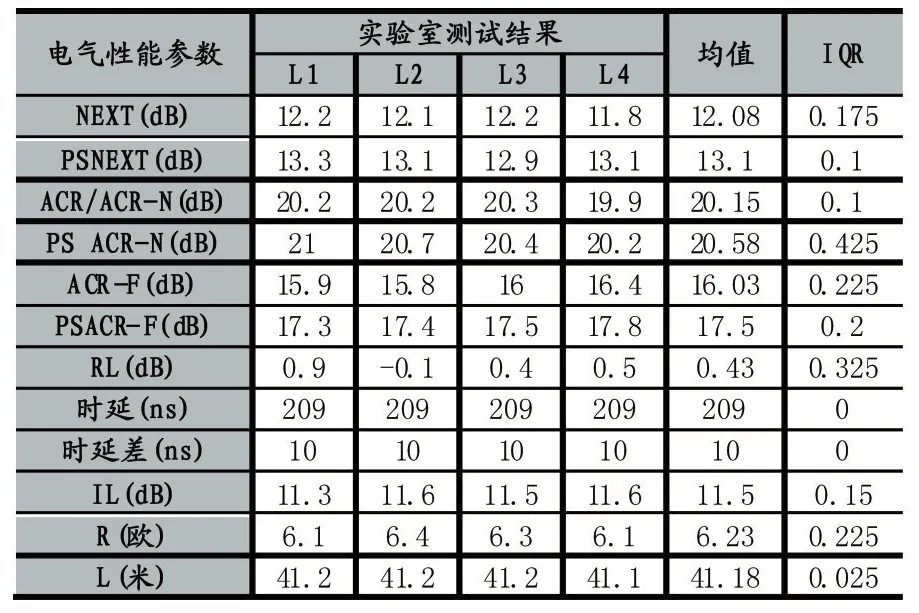
3.2 单因子分析



3.3 评价结果验证
4 结语
