计及需求响应电量约束的日前调度策略

陈培培， 包宇庆， 陈 刚，张金龙， 王 琦， 唐小波， 李天然

( 南京师范大学南瑞电气与自动化学院, 江苏 南京 210042)

0 引言

随着社会经济的迅速发展，资源、气候问题日益突出，增加可再生能源的利用已成为各国实现可持续发展的重要技术措施[1]。风能作为一种可再生能源，具有可以大规模开发利用的优势，将成为替代化石能源的重要能源之一。按照我国“可再生能源中长期发展规划”要求，到2020年可再生能源的将占能量消耗总量的15%，全国风电总装机容量将达到3×107kW[2]。然而由于风电日内波动幅度很大，反调峰特性明显[3]，大规模风电接入使得电网面临着严峻的新挑战[4-5]。

需求响应(demand response，DR)通过技术和经济手段相结合，合理调用需求侧资源来响应电力系统运行状态，提高电力系统稳定性。将DR纳入电力系统调度计划考虑范畴，具有削峰填谷[6]、满足稳定性要求[7]、抑制新能源波动[8]等优点，具有重要意义。

目前，已有不少相关文献研究风电并网调度模型。文献[9—10]针对风电并网引起的不确定性因素，考虑正负旋转备用，以经济性最优为目标建立含风电场的调度模型；文献[11]提出一种考虑风电预测误差带的调度优化模型；文献[12]提出了在多时间尺度内解决风能在电力系统中经济调度问题的随机规划框架。上述文献对节约火电资源，提高风能的利用率具有一定积极意义，但都是从发电侧角度考虑电网调度优化问题。文献[8，13]结合需求侧资源，针对发电成本最低问题，考虑分时电价和可中断负荷模型，有效提高系统经济性与风能利用率；文献[14]进一步以弃风电量期望最小为优化目标，建立兼顾发电成本与风电接纳水平的日前调度模型；文献[7]在保证系统可靠性与经济性的前提下，提出一种考虑短期随机安全约束的机组组合日前调度模型；文献[15]将备用容量作为机会约束条件，建立了融入DR并计及风险机会约束的日前调度模型。

将需求侧资源作为发电调度的补充，对电力系统的稳定运行具有重要意义[16]，目前少有文献研究考虑需求侧可控负荷电量约束的调度模型。可控负荷主要有温控负荷、电动汽车等，此类负荷有共同的特点，即具备一定的储热(冷)或者储存电量的能力。这类电器设备类似于储能设备，当电源突然切断时，设备内部的热(冷)量或者电量能够维持一段时间且基本不会对用户造成影响[18]。但由于其储能量不可能无限增加或减少，为了保证电力系统稳定运行，在调度模型中有必要增加可控负荷电量约束条件。因此本文综合考虑发电侧与需求侧资源，在传统调度模型中加入DR电量约束条件，建立日前调度模型。

1 数学模型

1.1 目标函数

在负荷和风电预测数据的基础上建立日前调度模型，以经济性最优为目标，通过合理安排火电机组的出力，使发电总成本最低，其目标函数如下：

(1)

(2)

Ui,t=pfcsxi,t

(3)

Di,t=pfcdyi,t

(4)

式中：t为时段号；i为机组号；Nt为调度周期时段数；Np为机组数；Pi,t为第i台火电机组在t时刻的输出功率；F(Pi,t)为火电机组发电成本；pf为燃料价格；a，b，c为发电机组的能耗特性系数；Ui,t与Di,t分别为火电机组启停成本；cs与cd分别为火电机组启停价格；xi,t与yi,t分别为第i台机组在t时刻的开启与关闭动作；pzZt为转移负荷的成本，pz为用户增加或减少用电的激励价格；Zt为需求响应在t时刻转移的负荷，Zt为正表示t时刻的负荷转移到其它时刻，Zt为负表示其他时刻的负荷转移到t时刻；Qt为风电场的切风量，pqQt为风电场的切风成本。

1.2 约束条件

(1) 功率平衡条件：

(5)

式中：Wt为风电场在t时段的风电预测功率，τt为t时段系统总负荷。

(2) 机组启停变量的约束：

(6)

式中：ui,t为第i台机组在t时刻的状态。

(3) 火电机组开关约束：

(7)

式中：xi,t为第i台机组在t时刻的开启动作；yi,t为第i台机组在t时刻的关闭动作。

(4) 火电机组输出功率上/下限约束：

(8)

式中：Pimax为第i台机组出力下界；Pimin为第i台机组出力上界。

(5) 火电机组爬坡速率约束：

-βi≤Pi,t-Pi,t-1≤αi

(9)

式中：αi为第i台机组相邻时段功率变化量上界，-βi为第i台机组相邻时段功率变化量下界。

(6) 潮流约束：

θref=0

(10)

节点功率平衡方程：

Pm+Qm-Mm=Im

(11)

式中：Pm是火电机组在节点m上的注入功率；Qm是风电场在节点m上的出力；Mm是节点m上的负荷；Im是节点m上的流入功率。

(7) 支路潮流约束：

(12)

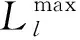
(13)

式中：θm与θn为节点m与节点n的电压相角；xl是节点m与节点n之间的支路l的电抗值。

(8) 可控负荷约束：

(14)

式中：Smax为调度周期内负荷的转移引起的电量变化，Smax=0表示所削减的负荷全部转移到其他时段，调度周期内用电量不发生变化。

(9) DR电量约束：

1.2.3 D 在进行人员培训时，需要对所有的门诊抽血人员进行相应的考核和培训，加深其应用印象。同时在日常工作中，也应当做好相应的风险预防和风险应急处理机制，使工作人员在进行日常医疗活动时，能够对风险进行预防，而在风险发生时也能够对其进行及时处理，降低影响范围。

可控负荷可等效为储能设备。对于电动汽车，其能量可以等效为电量；而对于温控负荷，其能量则可以等效为储存的热(冷)量，但是不论哪种，其具有的能量都不可能无限增加或减少。

换言之，可控负荷可转移电量是有限制的，为避免影响电力系统安全运行，需要增加需求响应的电量约束条件。

(15)

0≤E≤Emax

(16)

式中：E为可控负荷的电量；E0为调度周期起始时刻可控负荷的电量；Emax为可控负荷所能够转移的最大电量。

2 仿真算例

算例选取6节点系统，如图1所示，该系统含有3台火电机组以及1台风电机组。表1为火电机组相关数据[19]，表2为6节点系统预测负荷[7]以及风电的预测数据，采用适用于混合整数线性规划的软件YALMIP与ILOG CPLEX 12.5进行优化计算。

图1 6节点系统单线图Fig.1 One line diagram of 6-bus system

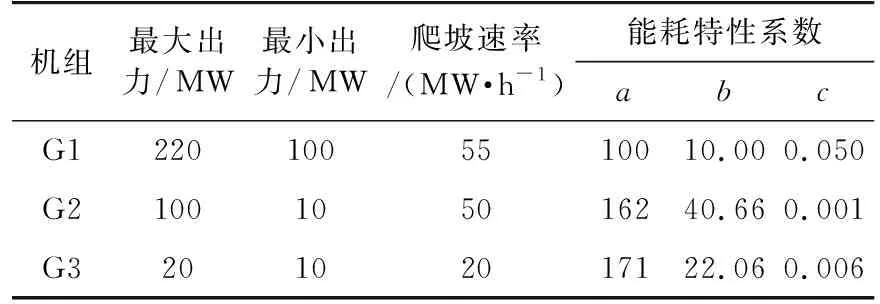
机组最大出力/MW最小出力/MW爬坡速率/(MW·h-1)能耗特性系数abcG12201005510010.000.050G2100105016240.660.001G320102017122.060.006

表2 6节点系统预测负荷与风电预测数据Tab.2 Forecasted load and wind power for 6-bus system

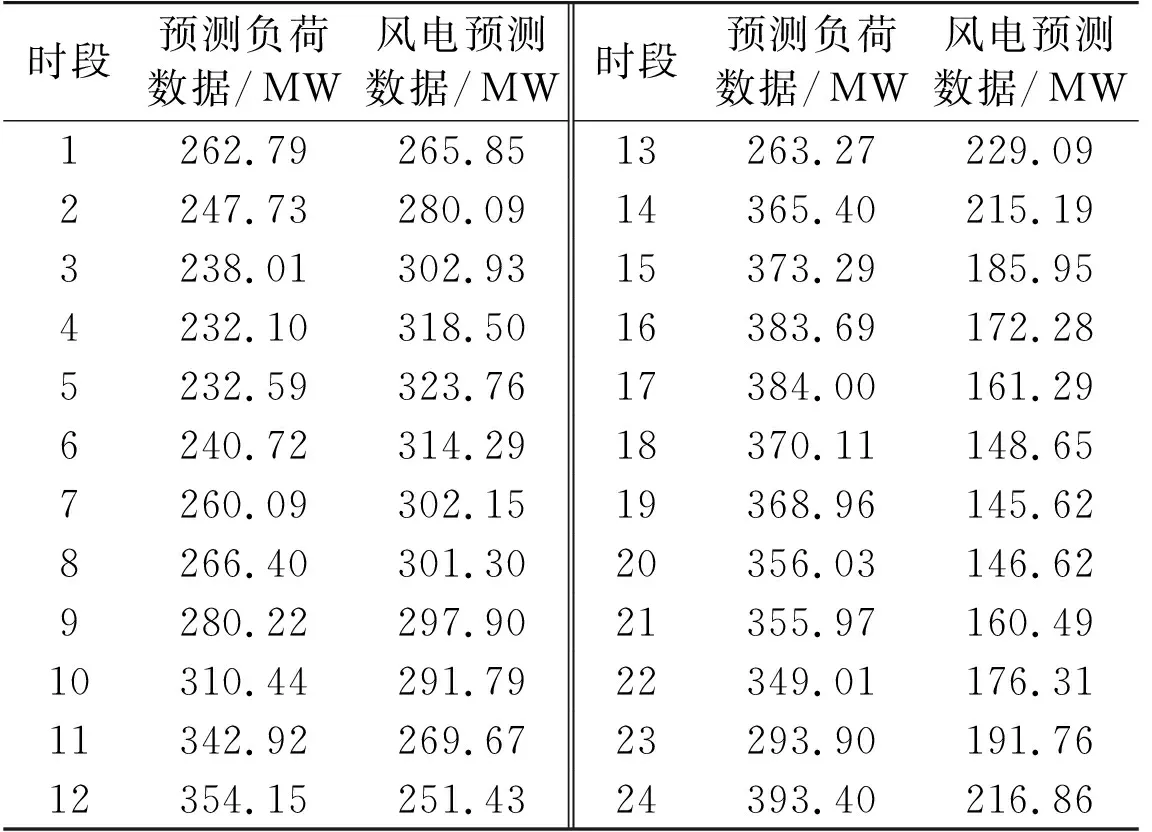
时段预测负荷数据/MW风电预测数据/MW时段预测负荷数据/MW风电预测数据/MW1262.79265.8513263.27229.092247.73280.0914365.40215.193238.01302.9315373.29185.954232.10318.5016383.69172.285232.59323.7617384.00161.296240.72314.2918370.11148.657260.09302.1519368.96145.628266.40301.3020356.03146.629280.22297.9021355.97160.4910310.44291.7922349.01176.3111342.92269.6723293.90191.7612354.15251.4324393.40216.86

为验证本文提出方法的有效性，采用以下3种模型进行对比分析：

模型Ⅰ：不考虑DR；

模型Ⅱ：考虑DR，不考虑DR的电量约束；

模型Ⅲ：同时考虑DR和DR的电量约束。

针对上述3种情况分别进行负荷预测，如图2所示。为了进一步说明电量约束条件的作用，本文比较了考虑与不考虑DR电量约束情况下的区别，此处假设可控负荷所能够转移的最大电量Emax为260 MW·h。

首先，为了得到调度周期起始时刻可控负荷的电量，假设式(15)中E0为0，代入调度后得到一天的可控负荷转移量，再估算出电量的实际初始值，传统方法中E0为30 MW·h，本文方法中E0为0 MW·h。

图2为考虑不同约束条件下的负荷预测结果。由图2可见，无论是否考虑DR电量约束，引入DR都可以优化负荷曲线，具有显著的“削峰填谷”的效果。

图2 不同情况下的预测负荷Fig.2 The forecasted load under different constrains

图3为不同约束条件下24时段的可控负荷转移量，考虑DR电量约束后，负荷转移量有所削减。在用电低谷时段，转移量为负，表示其他时段的负荷转移到该时段，可等效为对负荷充电；在用电高峰时段，转移量为正，表示该时段的负荷转移到其它时段，可等效为负荷放电。

图3 不同约束下的可控负荷转移量Fig.3 Transferred quantity of controllable load under different constrains

转移的电量与负荷充放电状态如图4所示。

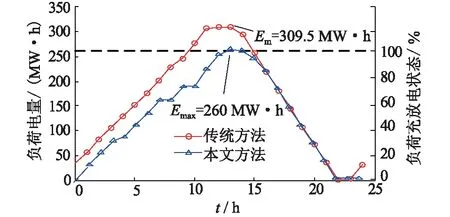
图4 不同约束下的负荷电量与充放电状态Fig.4 Load electricity quantity and charge and discharge status under different constrains

传统方法中，负荷在调度周期内最大电量为Emax为309.5 MW·h，负荷充放电状态达119.04%，超出了需求侧负荷所能够增减的最大电量限值260 MW·h；而考虑DR电量约束后，负荷所能够增减的电量被约束在最大电量变化范围内，有效防止负荷电量越限，从而保证系统运行的安全可靠。

以上例证说明了引入DR电量约束条件的必要性，下面分别比较可控负荷所能够增减的电量限值不同对优化结果的影响。引入电量的标幺值：

(17)

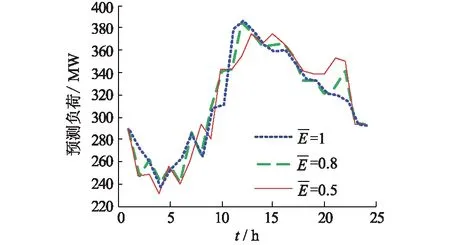
图5 不同电量约束条件下的预测负荷Fig.5 The forecasted load with different electricity quantity constraint

成本类型模型Ⅰ模型Ⅱ模型ⅢE=1E=0.8E=0.5发电总成本/万元12.45711.04911.65511.91312.354火电机组发电成本/万元12.31810.82911.42911.69712.154启停成本/元225225225225225切风成本/元1 165.0730.9995.51 099.51 255.5负荷转移成本/元012381040832520

从表3中可看出：

(1) 需求侧资源的引入降低了火电机组发电成本与风电机组的切风成本，使得发电总成本大大降低，提高了经济性；

(2) 在考虑DR电量约束后，由于需求侧可调度的负荷资源减少，负荷转移成本随之减少，但同时火电机组的发电成本与风电机组切风成本有所增加，最终的发电总成本也随之增加；

3 结语

本文以经济性最优为目标，综合考虑发电侧与需求侧资源建立了计及需求响应电量约束的日前调度模型。模型中引入DR可以提高系统调度运行的经济性，同时，在传统约束条件中加入需求侧可控负荷的电量约束条件对于保证系统安全稳定运行是必要的。通过仿真算例可以得到以下结论：

(1) 在日前调度模型中引入DR资源，可以有效降低发电成本，从而达到经济性最优的目标；

(2) 在考虑DR资源的日前调度模型基础上，本文模型增加了DR电量约束，虽然发电成本有所增加，但兼顾了需求侧资源实际上能够提供的最大电量值，可以有效防止可控负荷电量越限，提高系统运行的安全可靠性；

(3) DR电量限值不同，发电成本也将不同。更大的DR电量限值，意味着DR可以更多地参与到电力系统调度中，其发电成本也大大降低。

目前需求侧资源众多，能够参与调度的资源却很少，因此，发掘需求侧资源的潜力，在未来的调度中提出新的约束条件，对提高电力系统运行的经济性、稳定性具有重大意义。