Networked Control Approach for Distributed Generation Systems

Magdi S.Mahmoud and Mohamed Saif Ur Rahman

Abstract—Microgrid has emerged as an answer to growing demand for distributed generation(DG)in power systems.It contains several DG units including microalternator,photovoltaic system and wind generation.It turns out that sustained operation relies on the stability of these constituent systems.In this paper,a microgrid consisting of microalternator and photovoltaic system is modeled as a networked control system of systems(SoS)subjected to packet dropouts and delays.Next,an observerbased controller is designed to stabilize the system in presence of the aforementioned communication constraints and simulation results are provided to support the control design methodology.

I.INTRODUCTION

E CONOMIC challenges,technological advancements and environmental impacts are now demanding distributed generation in place of the conventional centralized generation[1].Power operation companies are now confronted with unprecedented difficulties in terms of meeting the load requirements,consumer satisfaction and environmental considerations.Thus,distributed generation has received good attention because of its potential to alleviate pressure from the main transmission system by supplying a few local loads[2].The waste heat generated from the fuel to electricity conversion is exploited by the distributed generation system with the help of microturbines,reciprocating engines and fuel cells to provide heat and power to the customers.Adding to the system distributed energy sources(DES)like photovoltaic(PV)panels,wind turbines,energy storage devices such as batteries and capacitors,generators and controllable loads.The distributed generators can extract energy from other renewable nearby systems and provide momentous contributions to future energy generation and distribution.Another noteworthy feature is that the carbon emission is reduced to a large extent satisfying the commitment of many nations concerning decrease of carbon footprints[3].However,the distributed generation faces technical issues regarding its connection to the intermittent renewable generation and feeble areas of the distribution network.Further,owing to the distinct behavior of the distributed generation unlike the conventional load,alteration in power flow results in problems.To counter the irregular behavior and increasing penetration of the distributed generation,the microgrid was introduced.

The microgrid has paved its way into distributed generation and looks promising for future prospects.It has the ability to respond to changes in the load,while decreasing feeder losses and improving local reliability.Basically designed to cater the heat and power requirements of local customers,it can serve as uninterruptible power supply for critical loads.Several control strategies for the microgrid have been proposed in the literature including PI controllers in[4]-[12].Robust H∞control is presented in[13]and[14]for the control of two distributed generation units.An optimal controller is presented for controlling the frequency and voltage fluctuations during islanded mode in[15].The inverters connected to these systems operate under imbalance conditions due to sensitive loads.This leads to switching harmonics,voltage and frequency variations in the microgrid system and disturbs the stability of the system.Thus modeling and control problems associated with microgrids including multiple distributed generation units are typically complex and interconnected in nature.

One efficient way to resolve the foregoing microgrid problem is to cast the integrated dynamic model into the SoS framework for better operation and organized control.The concept of SoS has opened up a new school of thought in systems engineering.SoS has emerged as a hot topic for research over the past few years.Although still in the infant stages,the concept of SoS has managed to achieve widespread acclaim.Being restricted to defense and IT,at one point of time,SoS has now entered a plethora of domains[16],[17].It is worth noting that a microgrid is a complex system comprising of a variety of systems which are nonlinear in nature and possess strong cross-coupling between them.Hence viewing the microgrid from an intelligent system of systems perspective is need of the hour.Moreover an efficient control methodology based on SoS has to be established in order to overcome the challenges posed by the microgrid.The concept of SoS is now widespread and has entered several domains including defense,IT,health care,manufacturing,energy and space stations and exploration to name a few.

Recent progress in analysis and design issues of networked control systems is reported in[18]-[22].Additional related work are published in[23].Networked control of system of systems has been introduced in[24].A control system consisting of a real time network in its feedback can be termed as a networked control system(NCS)[25].As mentioned in[24]that the need to design a SoS control system which can tolerate packet loss and delays is one of the prime challenges in SoS networked control,we considered a network which is subjected to both delays and non-stationary packet dropouts and the controller stabilizes the system in the presence of these communication issues.The controller design for such a networked control is presented in[26].A further extension is made in the controller design by introducing a distinctˆX matrix in the linear matrix inequality(LMI)that is used to obtain the controller gain matrices and a realistic approach is adopted to compute the gains.

The main objective of this paper is to formulate a SoS framework including a communication network for the distributed generation units of a microgrid and consequently design a feedback controller to guarantee closed-loop stabilization in the presence of communication constraints,network delays and packet dropouts.The considered microgrid system comprised two sets of microalternator and PV panels as distributed generation units,which are eventually connected to a load and the main grid.To achieve our objective,the work reported here in combines two parts:a detailed modeling and analysis part leading to establish a stabilizing controller and real-time implementation part to illustrate the performance.This latter part is achieved at the SoS research lab at KFUPM using pilot-scale lab equipment to build an experimental microgrid including up to 12 DG units.The simulation tools are Matlab-Simulink environment,particularly the products Simscape Power Systems Examples and RAPSim an open source simulation software for microgrids.

The main contributions of this work are:

1)A generalized approach to modeling microgrids with multiple distribution generation units is developed based on SoS framework.This is a novel approach in the context of renewable energy systems.

2)The microgrid system incorporated communication network to enable processing control signals and power measurements.

3)An improved output feedback networked controller is constructed to stabilize the microgrid system in presence of delays and non stationary packet dropouts.

The paper is organized as follows.A brief introduction of microgrids and SoS is presented in Section I.Detailed modeling of both the microalternator and PV system is presented in Section II.A combined framework of microalternator and PV system connected to a load and the main grid is proposed.A state space representation of the combined system is presented.Further the detailed networked control system,its stability analysis and controller design is explained in Sections III and IV with relevant theorems.The controller design is implemented on the proposed framework and simulation results are shown for two sets of PV and microalternator systems.Finally conclusions are drawn and the effectiveness of the proposed framework and control strategy is discussed.

II.MODELING OF THE MICRO ALTERNATOR-PV SYSTEM

To model the microgrid system consisting of microalternator and PV system,we consider the separate modeling of microalternator and PV system initially.After modeling both these individual systems,we integrate them into a microgrid system which is connected to a load and the main grid.Two sets of such systems are considered eventually which form a SoS structure for the microgrid system.

A.Micro Alternator

The swing equation of the alternator can be written as two first order differential equations[27]:

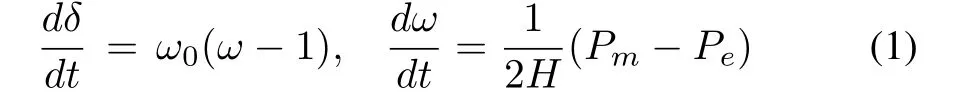
where δ and ω are rotor angle and rotor speed.Pmand Peare mechanical power input and electrical power output of the generator.The internal voltageis given by

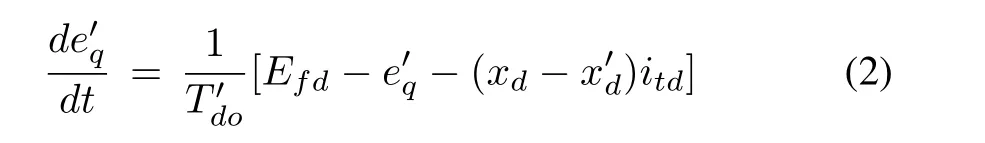
where xd,andare the d-axis synchronous resistance,transient reactance and open circuit field constants respectively.is the voltage behind the transient reactance along q-axis.An IEEE type ST is used for the voltage regulator excitation.

where Efdis the field voltage along d-axis,KAand TAare the gain and time constants of the exciter.Fig.1 shows a microalternator connected to the main grid.

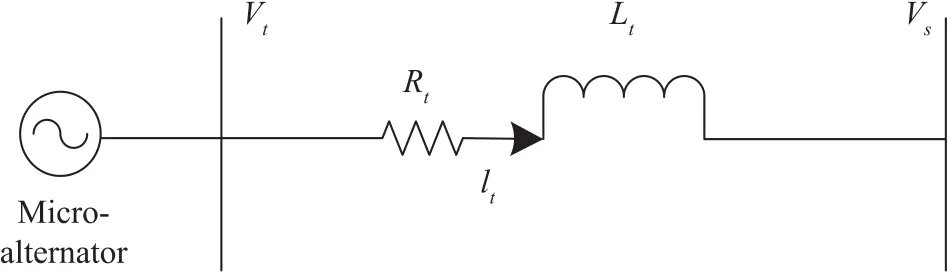
Fig.1.Microalternator connected to grid.

The terminal voltage of the alternator is given as

In d-q terms it becomes

The real part can be written as

and the imaginary part can be written as

Substituting x1=(+xt)and x2=(xq+xt)and solving for itdand itq,we obtain

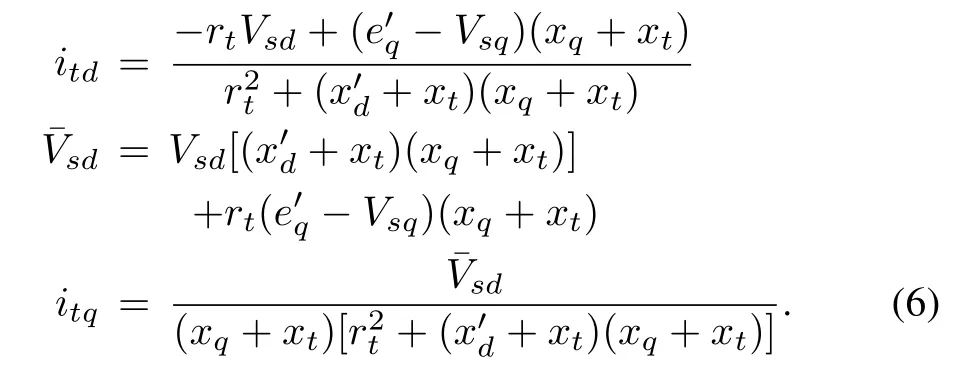
Hence,the terminal voltage and power output of the alternator are given as

By perturbing the above nonlinear equations around a normal operating point and letting[δ,ω,,Efd]as the states,we obtain the linearized state equations

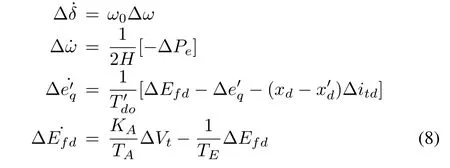
along with the generator output current

The first-order difference of itdcan be obtained from(6)as

Similarly obtaining the change in the q-axis generator output current as

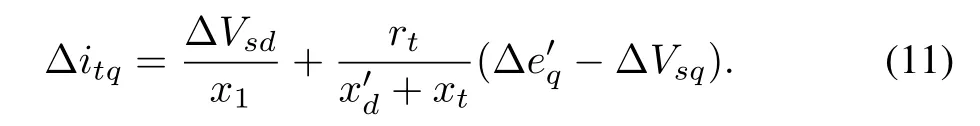
Further algebraic manipulation yields

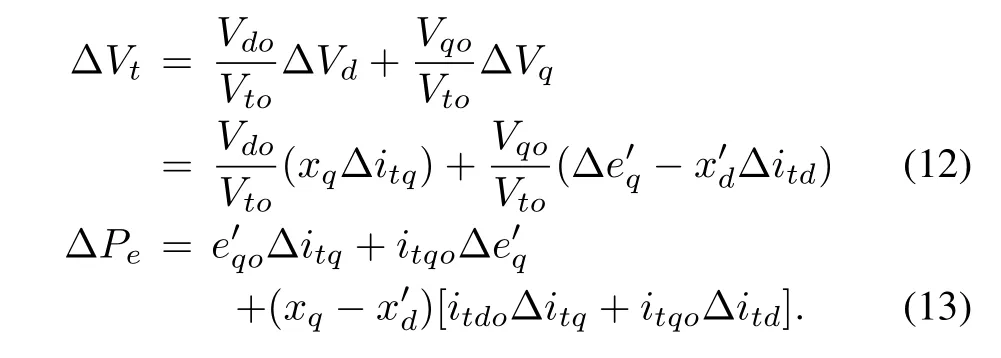
B.Photovoltaic System

A mathematical expression describing the I-V characteristics of a solar cell has been studied extensively.An equivalent model of a solar cell shown in Fig.2 includes a photo diode,a shunt resistor depicting leakage current and a series resistor representing an internal resistance to current flow.The difference between photovoltaic current Iphand sum of normal diode current IDand leakage current in the shunt resistor Ishgives the net output current from the PV cell.

Fig.2.Model of PV cell.

The diode current IDis given as

where Ipvis the cell current,Vpvis the cell voltage,Isis the reverse saturation current(depends on temperature),n is the ideality factor,Rsis the series resistance,Rshis the shunt resistance,VT(=k T/q)is the thermal voltage,k is Boltzmann constant,T is working temperature of the cell and q is the charge of the electron.

The solar irradiation and the working temperature of the cell determines the photo current.At given cell temperature T,the photo current can be expressed as

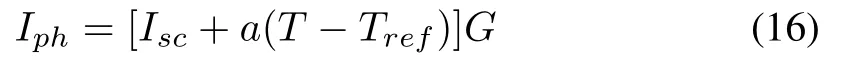
where Iscis the short current of the cell at 250C and 1kW/m2,a is the temperature coefficient of Isc,Trefis the reference temperature of the cell and G is the irradiation in kW/m2.

The reverse saturation current also depends on temperature and can be expressed as

where Isrefis the saturation current of the cell,Egis the energy band gap of the semiconductor used in the solar cell.The characteristic equation of the cell from the approximate model is given as

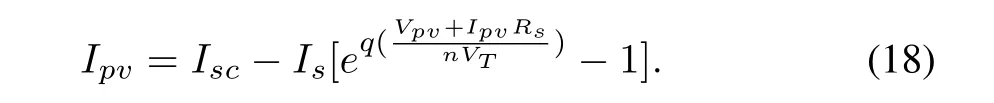
Because of the fact that the power generated by a solar cell is low,multiple solar cells are connected in series and parallel to generate power in the range of watts.Thus the characteristic equation of the photovoltaic array consisting of Nsseries and Npparallel modules can be derived from the PV cell equation mentioned above

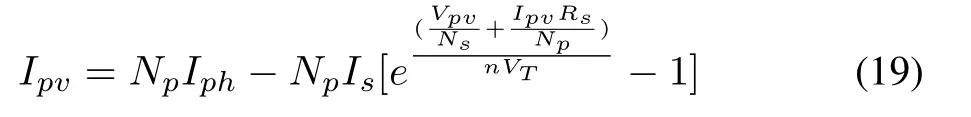
which is a nonlinear current voltage relationship of a PV array.Alternatively,it can be rewritten as

This can be iteratively solved using Newton-Raphson algorithm[28]of the form

where Esis a prescribed tolerance and xnis the n th solution.Letting

Since f0(VT)=1,the recursive formula(20)can be written as

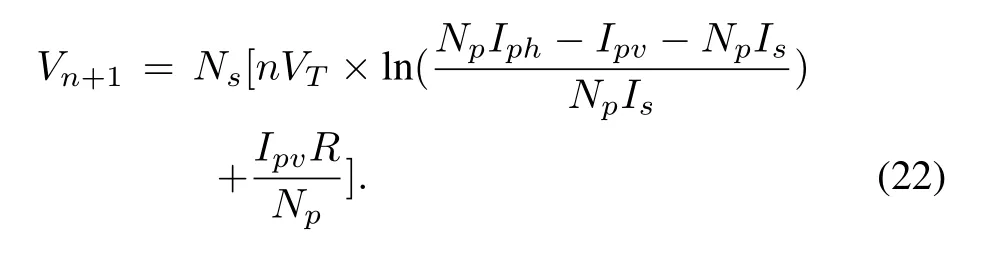
C.Power Conditioning Unit of PV System

The power conditioning unit(PCU)consists of devices needed to connect the PV array to the microgrid[29].The significant components of the PCU are

·DC/DC converter

·DC link capacitor

·Inverter

·Output filter circuit

1)DC/DC Converter Model

The primary function of the DC/DC converter is to either increase or decrease the DC output voltage.Out of the various topologies of DC/DC converters,buck and boost converters are the more fundamental ones.Because the PV output voltage has be to stepped up,a boost converter is used in this case.A typical converter configuration is shown in Fig.3.The boost converter steps up the DC voltage level.It consists of an inductor,a diode and a power electronic switch.

Fig.3.DC/DC converter configuration.

The dynamics of the converter can be expressed as

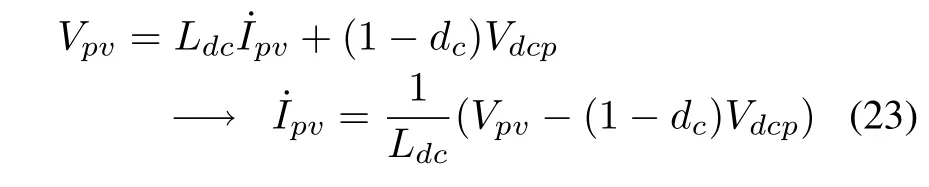
where Ldcis the inductance of the converter and dcis the duty cycle defined as the ratio of ON period to the switching time period(T).

2)DC Link Capacitor Model

The DC link capacitor functions as an energy storage and if lter for the DC voltage.

By applying Kirchhoff current law(KCL)at the DC-link node,the dynamics of the DC link capacitor can be obtained as

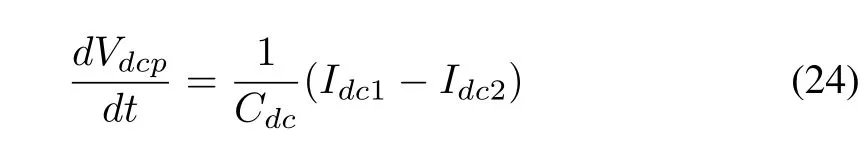
where Idc1=(1-dc)Ipvand Idc2is the input current to the inverter,which is derived later in this section.Vdcis the voltage across capacitor Cdc.

3)Inverter Model

The inverter is responsible for the conversion of the PV array DC output and giving it to the grid at an appropriate frequency.A voltage gain model of a voltage source inverter(VSI)operating in PWM mode is considered as shown in Fig.4.

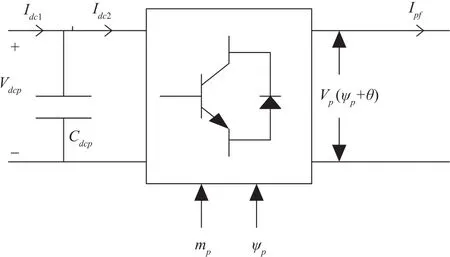
Fig.4.Inverter model.

The power on DC side of the inverter is given as

The instantaneous active power on the AC side of the inverter is expressed as

where Vpand Ipfare the inverter output voltage and inverter output current respectively.In d-q terms,Vpand Ipfcan be expressed as

Little algebra yields the power relations

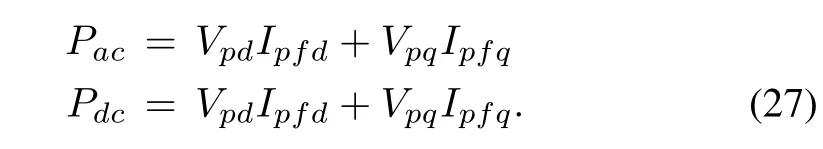
During its operation in PWM mode and referring to Fig.4,the output voltage of the inverter can be written as

where mpis the modulation index and ψpis the phase angle of the inverter.In d-q terms,this becomes

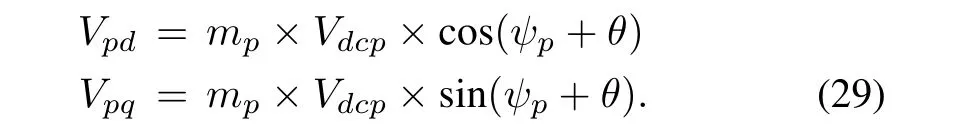
Finally,we obtain the expression for Idc2as

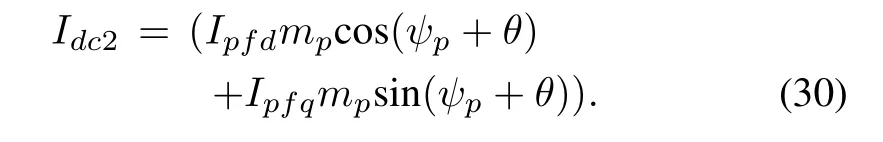
4)LC Filter and Coupling Inductance Model

The purpose of using a low pass filter is attenuation of switching frequency ripple of the output voltage of an inverter.The filter is a T section of an RL circuit shunted by a capacitor.While the inductor blocks high frequency harmonics,the capacitor stops low frequency harmonics.Collectively,they block most of the harmonics,thereby reducing ripples from going through the system[30].By applying KCL around the PV inverter and filter capacitor,we obtain a nonlinear relation as

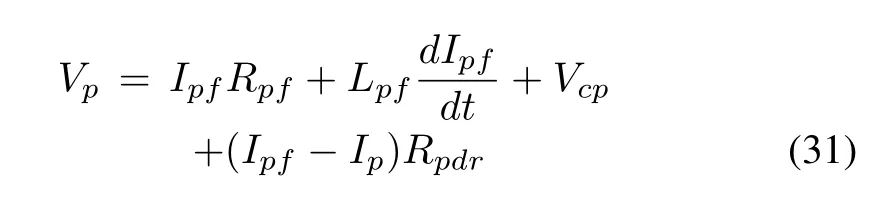
where Rpfis the filter resistance,Lpfis the filter inductance,Rpdris the damping resistance and Vcpis the capacitor voltage.Expressing in d-q frame,then(31)can be written as

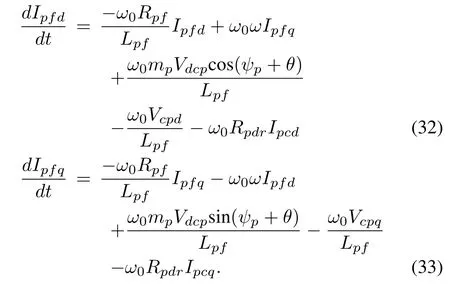
By coupling the transmission line between microgrid and PV filter capacitor,we obtain a nonlinear equation as

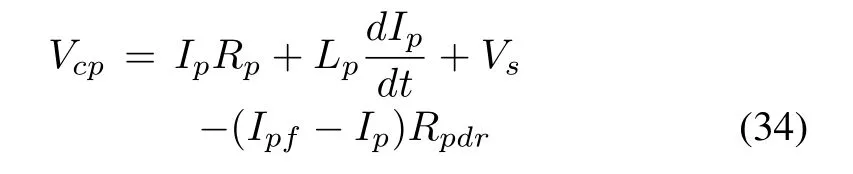
Rewriting in d-q terms,we have

where Ipis the coupling current,Rpis the coupling resistance and Lpis the coupling inductance.The voltage across the capacitor is given as

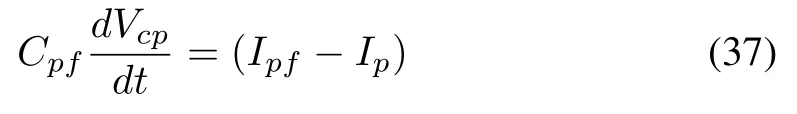
where Cpfis the filter capacitor.Once again in d-q terms,we get

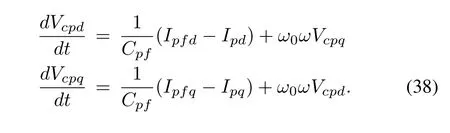
5)Linearized Model of the PV System

A linearized model of the PV system includes a small signal model of characteristic equation of the PV array and power conditioning unit.From(28)the characteristic equation of the PV arrays is

Making first-order changes of(20)with VT=Vpv,we get

By linearization each of the components of the power conditioning unit,a small signal model can be readily obtained.The linearized state equations are given as[29]

The voltage across the filter capacitor

III.INTEGRATED MICROALTERNATOR-PV SYSTEM MODELING

In the sequel,we consider a system where the microalternator and the PV system are the supply sources for a combined system.This eventually means that we have a microgrid with two distributed generation units.The modeling proceeds done in two parts.Initially both subsystems are modeled individually as presented in the earlier sections.An integrated modeling approach is presented here in this section from a novel view.

The microalternator-PV system is modeled to represent a system of systems,where two different subsystems are operating independently to achieve a common goal.There exists an integration between the two subsystems which is clearly evident from 5.It shows that both systems are connected through a common bus having voltage Vs.Eventually,the integrated system is connected to the main grid and a load.

In the end,the combined model consisting of both systems is considered for the networked control system(NCS)design implementation.For this reason,the state matrices shown are for the overall system.However,the A matrix for the alternator was given just to give an idea about the four states of alternator that are taken into account for the overall system.It is to be noted that the overall system matrices incorporate states and dynamics from both systems forming an integrated microalternator-PV system.Hence,A,B and C matrices are given only for the overall system.The A matrix of the microalternator is given just to describe which states are considered in the main system.

Fig.5 shows a microgrid system with a microalternator and PV generator along with a load connected to the main grid.All of these are connected through a common bus having voltage Vs.Microalternator and PV system dynamics have already been explained above.Both the systems had components of Vsalong d-q axes.Now to get a closed form representation of the combined state model,Vsdand Vsqhave to be expressed in terms of the selected states.For this we apply KCL at the common bus Vs,which gives

Fig.5.Combined system.

where It,Ip,Iband Ilare microalternator output current,PV output current,grid current and load current respectively.Considering the d-q components of these currents,we get

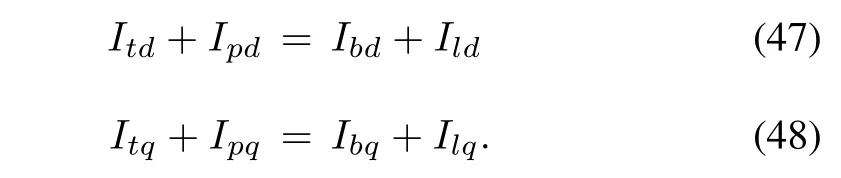
Further,we express the non-state currents(Itd,Itq,Ibd,Ibq,Ild,Ilq)as functions of Vsdand Vsq.However,the microalternator output currents Itdand Itqare already previously presented in terms of Vsdand Vsq.

Load Current:

At the microgrid,the load is modeled as admittance Y=g-jb.The load current is Il=VsY

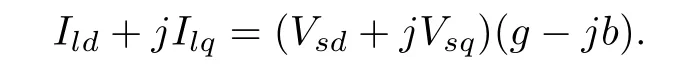
Equating real and imaginary parts,we get

Grid Current:

The main grid current Ibis given as

Equating real and imaginary parts

Standard manipulations yield the bus voltage components Vsdand Vsqas

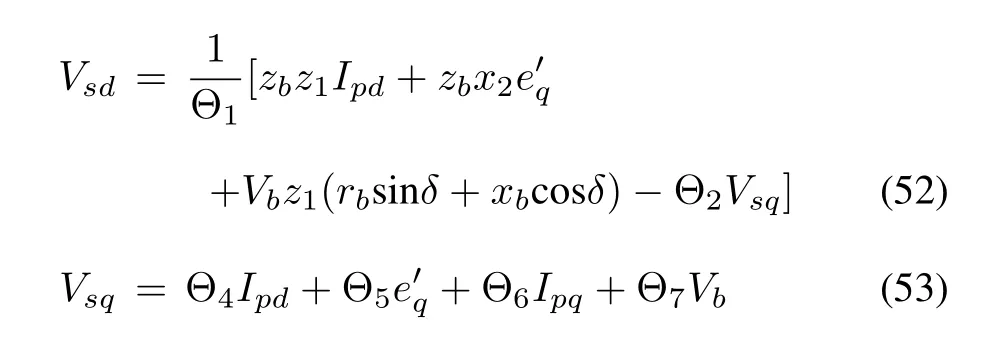
where

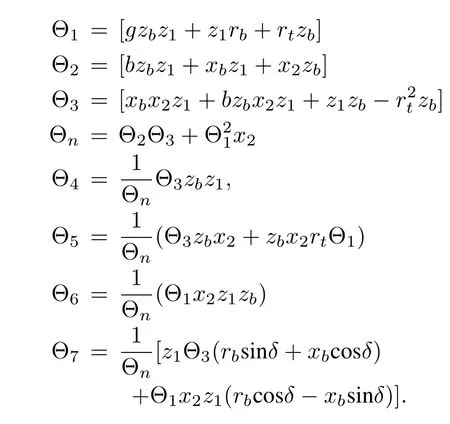
Linearized Model of the Combined System:

A linearized model of the combined system is obtained by expressing the linearized microgrid voltage components(ΔVsd,ΔVsq)along d-q axes in terms of the selected states.First-order analysis shows that

where

Similarly,we also obtain

Finally,the values of ΔVsdand ΔVsqare substituted in the linearized equations of the individual component models to obtain the closed-form equation.Selecting the states as[δ,ω,e0q,Efd,Ipv,Vdcp,Ipfd,Ipfq,Ipd,Ipq,Vcpd,Vcpq]Tand the control input as[mp,ψp],we consequently obtain the state matrices for the combined microalternator-PV system.

IV.NETWORKED CONTROL SYSTEM MODELING

Consider the microgrid with two sets of microalternator and PV system representing a SoS-NCS with random communication delays,where the sensor is clock driven and the controller and the actuator are event driven.The discrete-time linear time-invariant plant model is as follows:

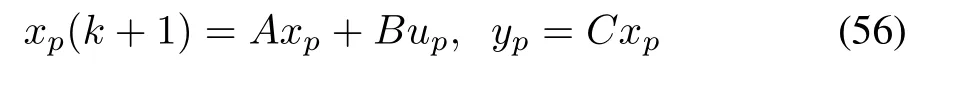
where xp(k)∈ Rnis the plant’s state vector and up(k)∈ Rmand yp(k) ∈ Rpare the plant’s control input and output vectors,respectively.A,B,and C are known as real matrices with appropriate dimensions.

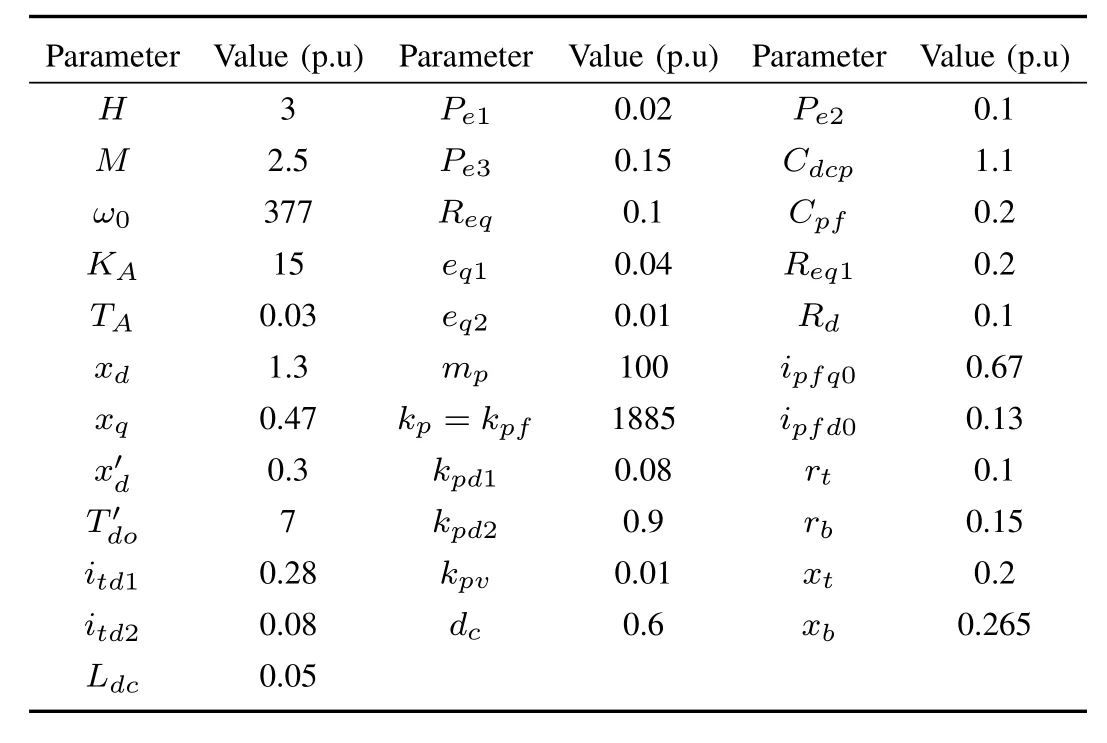
TABLE IPARAMETERS OF THE MICROGRID SYSTEM

Remark 1:We note that the developed renewable energy model is formulated in linearized continuous-time form as it emerges from physical considerations.For all practical purposes,we seek a discrete-time system of the type of(56).As will be mentioned in the simulation results section,the microalternator-PV system containing A,B and C matrices are discretized at a sampling time of 0.01 seconds.This is selected after a series of computer simulation experiments based on the closeness of the step-response of the linearized continuous model and its discretized counterpart.

For a more general case,we assume that the measurement after passing through the network exhibits a randomly varying communication delay and is described by[26]

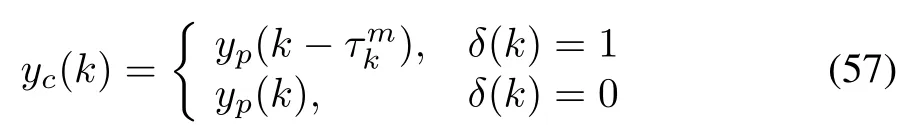
where pkassumes discrete values,see Table II.Two particular classes can be considered:Class 1:pkhas the probability mass function in Table II where qr-qr-1=constant for r=2,...,n.This covers a wide range of cases including

TABLE IIPATTERN OF pk

1)If there is no information about the likelihood of different values,we use the uniform discrete distribution,ri=1/n,i=1,2,...,n,

2)If it is suspected that pkfollows a symmetric triangle distribution,we use the following function:

i)If n is even,ri=a+jd,j=0,1,...,n/2 and ri=a+(n-j)d,j=0,1,...,n/2+1,n/2+2,...,n,where na+dn(n-1)/4=1,

ii)If n is odd,ri=a+jd,j=0,1,...,(n-1)/2 and ri=a+(n-j)d,j=0,1,...,(n+1)/2,(n+2)/2,...,n,where na+dn(n-1)2/4=1

3)If it is suspected that riis a decreasing linear function,we use ri=a-jd,j=0,1,...,n where na-dn(n-1)/2=1

4)If it is suspected that riis an increasing linear function,we use ri=a-(n-j)d,j=0,1,...,n where na-dn(n-1)/2=1

Class 2:pk=X/n,n＞0 and 0≤X≤n is a random variable that follows the Binomial distribution B(q,n),q＞0,that is

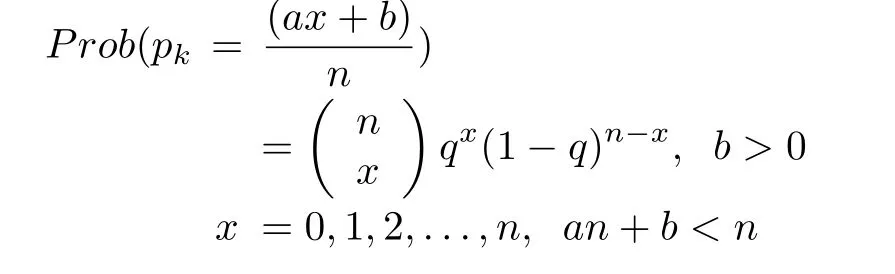
Remark 2:It is significant to note that the case P rob{δ(k)=1}= δ,where δ is a constant value,is widely used in majority of results on NCS.In this paper,we focus on nonstationary dropouts.

When the full state information is not available and the time delay occurs on the actuation side,it is desirable to design the following observer-based controller[26]:

Observer:

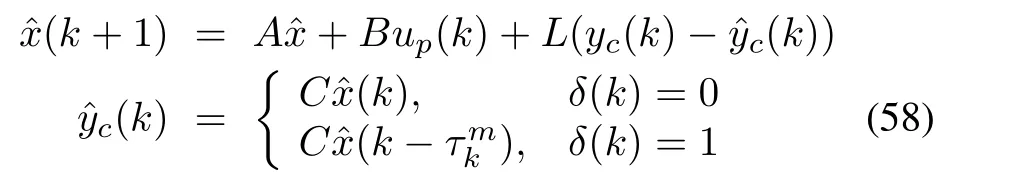
Controller:

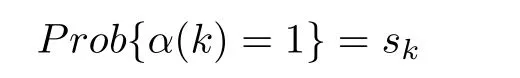
where skassumes discrete values.By similarity,a particular class is that skhas some probability mass function as in Table III,where sr-sr-1=constant for r=2,...,n.

TABLE IIIPATTERN OF sk

In this paper,we assume thatandare time-varying and have the following bounded condition:

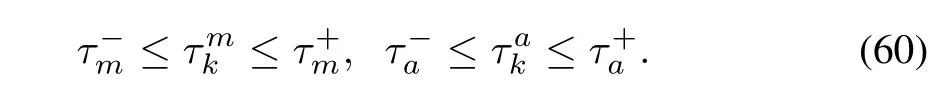
Define the estimation error by e(k)=xp(k)-ˆx(k).Then,it yields

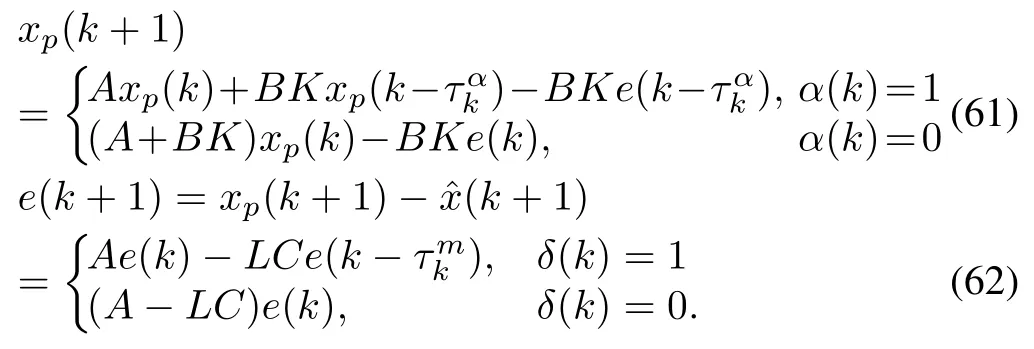
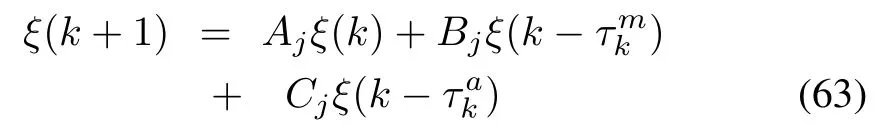
where{Aj,Bj,Cj,j=1,...,4}and j is an index identifying one of the following pairs{(δ(k)=1, α(k)=1),(δ(k)=1, α(k)=0),(δ(k)=0, α(k)=0),(δ(k)=0,α(k)=1)}:

Remark 3:It is remarked for simulation processing that we can express(61)and(62)in the form

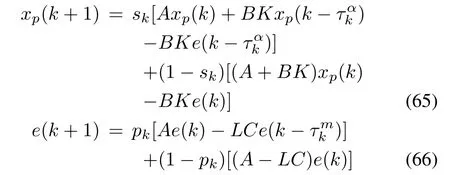
where the values of the random variables pk,skare generated in the manner discussed earlier.

Remark 4:It is important to note from(64)that

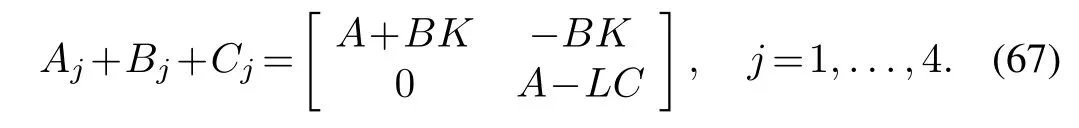
The interpretation of this result is that Aj+Bj+Cjrepresents the fundamental matrix of the delayed system(63),

which must be independent of the mode of operation.This will help in simplifying the control design algorithm.

The aim of this paper is to design an observer based feedback stabilizing controller in the form of(58)and(59)such that the closed loop system(63)is exponentially stable in the mean square sense.Our approach is based on the concepts of switched time-delay systems[31].For simplicity in exposition,we introduce

where IE[σi]is the expected value of σi,i=1,...,4.Since we assume that δ(k)and α(k)are independent random variables,then it follows from(68)that

V.DESIGN RESULTS

In this section,we will thoroughly investigate the stability and controller synthesis problems for the closed-loop system(63).First,let us deal with the stability analysis problem and derive a sufficient condition under which the closedloop system(63)with the given controller(58)and(59)is exponentially stable in the mean square sense.Extending on the basis of[32],the following Lyapunov function candidate is constructed to establish the main theorem

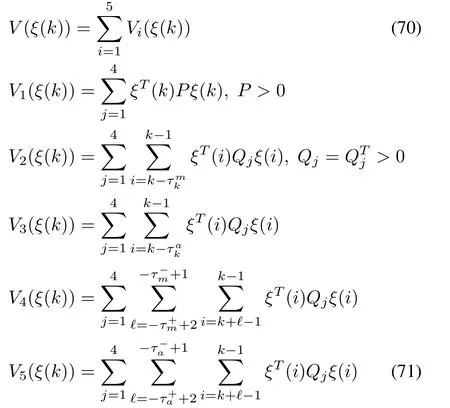
It is not difficult to show that there exist real scalarsµ＞0 and υ＞0 such that

Remark 5:By carefully considering Remark 4 in view of model(12),it is justified to select matrix P to be the same for all operational modes,hence independent of j,while keeping matrix Qjdependent on mode j.

We now present the analysis result for system(12)to be exponentially stable.

Theorem 1:Let the controller and observer gain matrices K and L be given.The closed-loop system(12)is exponentially stable if there exist matrices 0＜P,0＜QTj=Qj,j=1,...,4 and matrices Ri,Si,and Mi,i=1,2,such that the following matrix inequality holds[26]

where

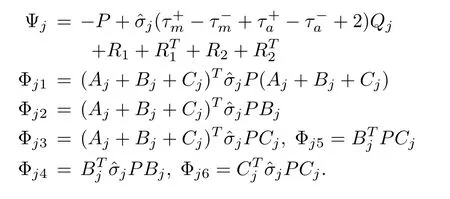
Proof:Defining y(k)=x(k+1)-x(k),one has

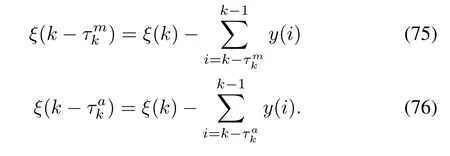
Then the system(12)can be transformed into

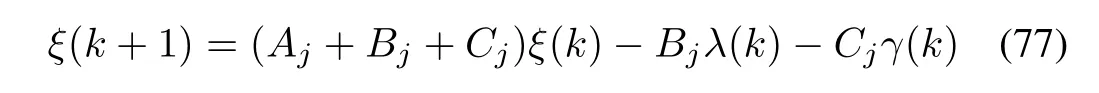
where

Evaluating the difference of V1(ξ(k))along the solution of system(77),we have

A straightforward computation gives

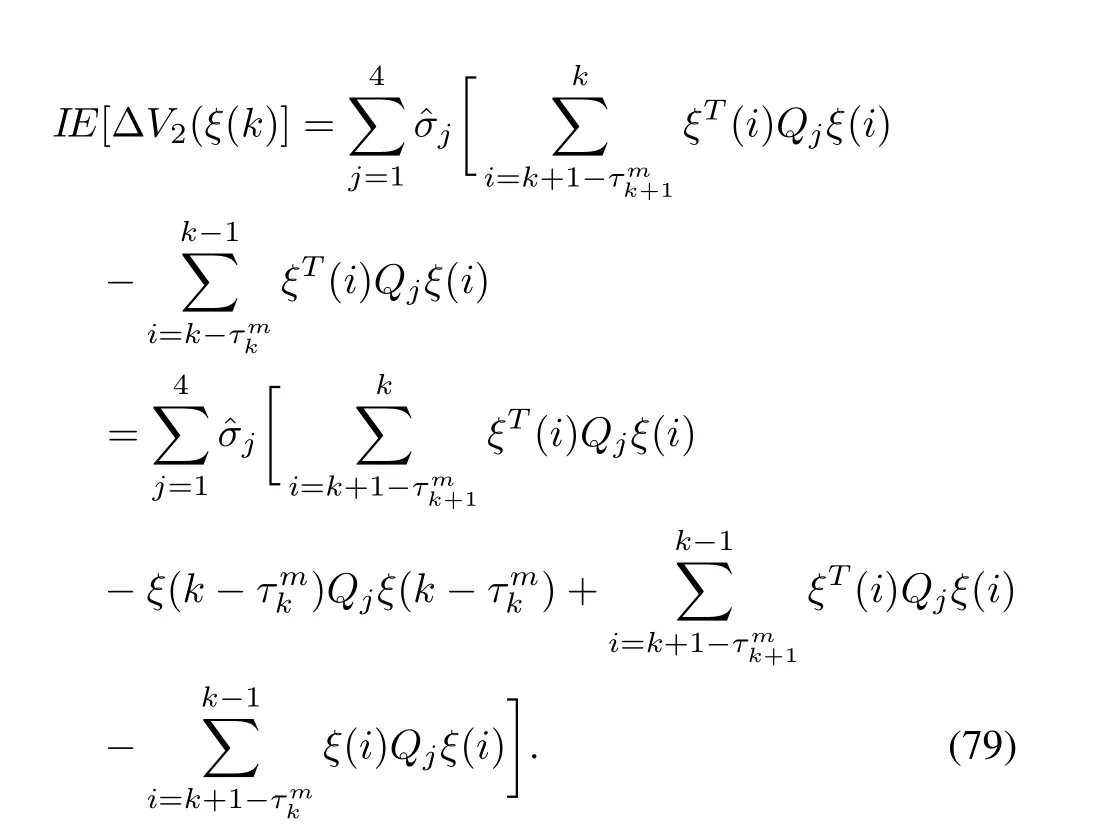
In view of

We readily obtain

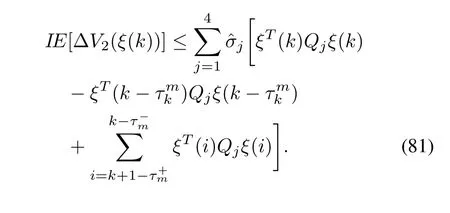
Following parallel procedure,we get

Finally,

It follows from(75)and(76)that:

Therefore,for any appropriately dimensioned matrices Ri,Siand Mi,i=1,2,we have the following equations:

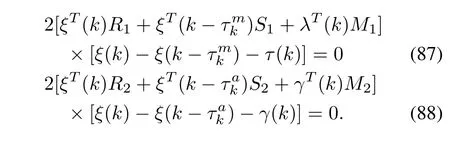
On combining(78)-(88),we reach

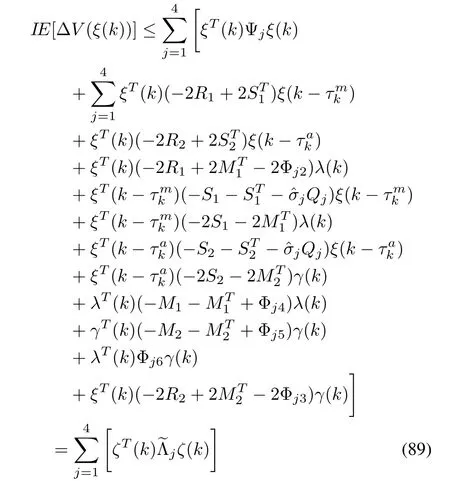
where

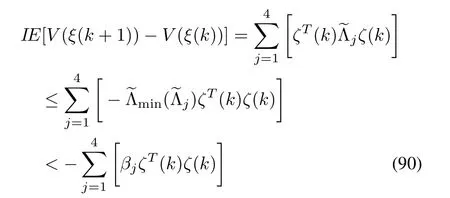
where

Inequality(90)implies that IE[V(ξ(k+1))-V(ξ(k))]＜-φV(ξ(k)),0＜ φ ＜ 1.In the manner of[33],we get

Therefore,it can be verified that the closed-loop system(12)is exponentially stable.

A solution to the problem of the observer-based stabilizing controller design is provided by the following theorem:

Theorem 2:Let the delay bounds τ+m, τ-m, τ+a, τ-abe given.Evaluate the quantitiesˆσj,j=1,...,4.Then,the closed-loop system(12)is exponentially stable if there exist matrices 0＜ X1,X2,Y1,Y2,Z1,0＜ Ξj,j=1,...,4 and matrices Πi, Υiand Γi,i=1,2,such that the following matrix inequality holds for j=1,...,4:

where the gain matrices are given by

Proof:Define

then matrix inequality(73)can be expressed as

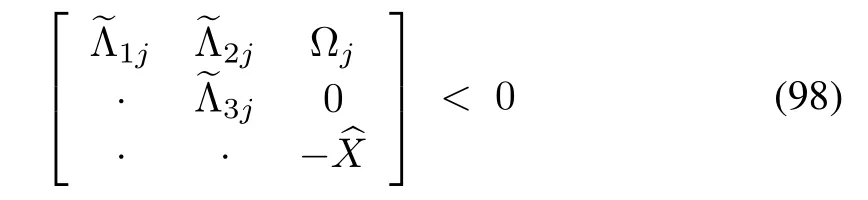
Applying the congruence transformation

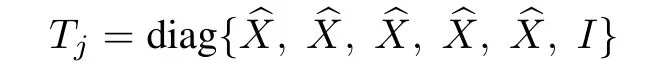
to matrix inequality in(98)and manipulating using(92)and

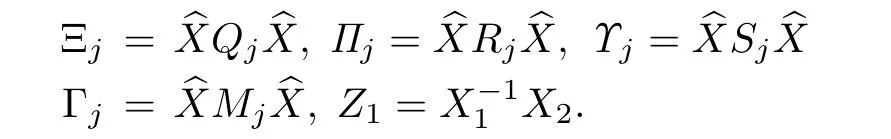
We readily obtain matrix inequality(91)subject to(94).

Remark 6:Expanding the microgrid to accommodate additional number of distributed generation units will eventually lead to increase the static computational burden as well.However using linear matrix inequalities as efficient numerical tool makes the job of determining the feedback gains becomes moderate.Moreover,it is executed off line and performed only once.

Remark 8:It is remarked that the implementation of Theorem 2 is on-line in nature as it requires calling random generators to pick-up numbers corresponding to the scalars ˆσ1,...,ˆσ4and to evaluate the probabilities in model(65)and(66)to compute the state and error trajectories.This represents a salient feature not shared by other methods for networked control design under unreliable communication links.

Remark 9:In this paper,theˆX matrix considered in Theorem 2 is distinct from the one in[26].TheˆX matrix incorporates two different elements X1and X2unlike the ˆX matrix in[26]which contains the same element X.This extension results in a distinct LMI termˆΩjgiven in(41).Further,the expression for calculating the controller and observer gains(K and L)is also different from[26]This is done to present a more realistic approach in determining the controller and observer gains.

Remark 10:The networked control system model considered in this paper is distinct from the one presented in[26].The model represents a typical SoS networked control model consisting of a sensor suite and an ad-hoc network for multiple subsystems.Moreover the illustrated example for the proposed control strategy is exclusively a microgrid SoS.

VI.SIMULATION RESULTS

In this section,the microgrid system which is modeled as a networked control SoS is simulated in the SoS research lab at KFUPM using pilot-scale lab equipment to build an experimental microgrid including up to 12 DG units.The simulation tools are MATLAB-Simulink environment,particularly the products Simscape Power Systems Examples and RAPSim an open source simulation software for microgrids.A singleline diagram of the microgrid under consideration is depicted in Fig.6.

Fig.6.Single-line diagram of the microgrid under consideration.

The output feedback controller design is implemented which stabilizes the system in presence of packet dropouts and delays.The parameter values given in Table I are substituted in the state matrices A and B presented earlier in this paper.Both the sets of PV-microalternator system are similar in nature but have different parameter values.

The controller and observer gains can be obtained by using the relation K=Y1and L=Y2C†,X1,X2,Y1,Y2can be found by solving the LMI(91)in Theorem 2.The values of α and δ are set at 0.1 each.The measurement delay is varied from 1 to 5 and the actuation delay is varied from 3 to 9.The system is discretized at a sampling time of 0.01 seconds.This is selected after a series of computer simulation experiments based on the closeness of the step-response of the linearized continuous model and its discretized counterpart.

The NCS is modeled in such a way that delays are accommodated in both the measurement as well as the actuation channel.The delays are generated by employing random number generators.The number obtained from the uniform random number generator is compared to a variable probability pkexplained earlier in the paper.If the random generated number is less than pk,then the output of the comparator is high meaning a delay has occurred.Otherwise,if the output of the comparator is low,there is no delay.This is accomplished by using the variable functional delay block in Simulink.

The gain matrices obtained for both sets are shown above.

Figs.7-18 shown above represent the state response of both sets of microalternator-PV system named as set 1 and set 2.Each state represents a typical dynamics of the system.

The simulation results elucidate the effectiveness of the proposed control methodology.Two sets of the microalternator-PV system are considered which have distinct parameter values.As evident from the graphs,the output feedback controller stabilizes the system in presence of delays and packet dropouts.It can be observed from the state-wise response that each state of both the sets possessing different values is stabilized by the controller an a reasonably less time with minimum overshoot and very less oscillations.Thus,the simulation results obtained significantly exhibit the controller responses for different parameter values.Moreover,stabilization in presence of communication issues such as packet dropouts and delays further explain the effectiveness of the controller.It is also to be noted that the state response of both sets of microalternator-PV system is presented in one graph to demonstrate the ability of the controller to stabilize the system irrespective of the parameter values.

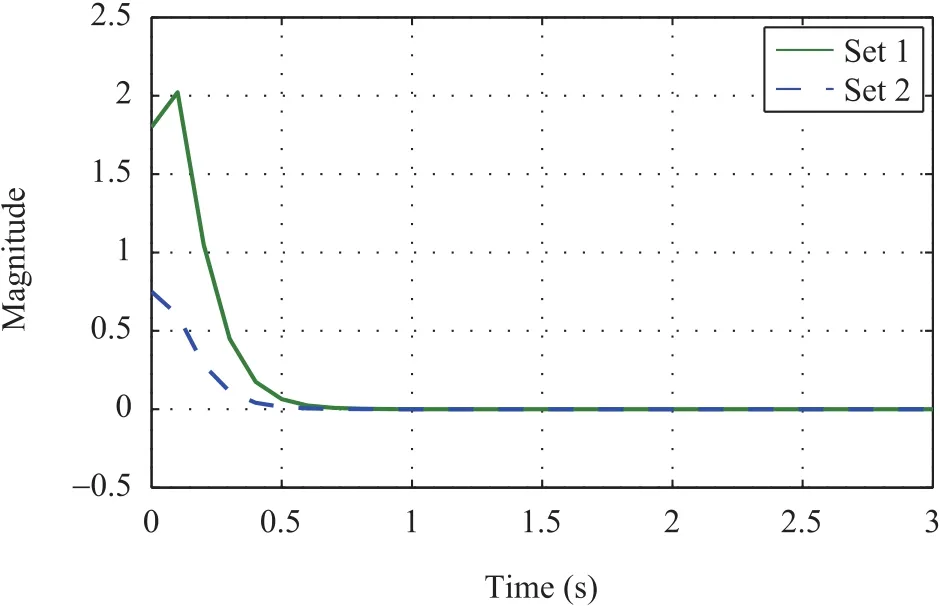
Fig.7.Rotor angle of the microalternator.

Fig.8.Rotor speed of the microalternator.

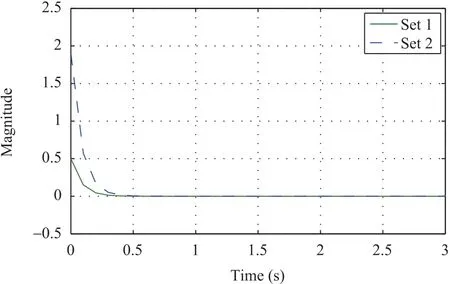
Fig.9.Internal voltage of microalternator along q-axis.

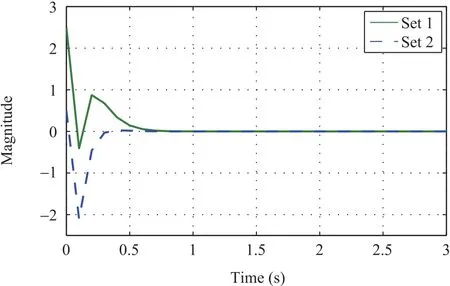
Fig.10. Field voltage of microalternator along d-axis.

Fig.11. Photovoltaic cell current.

Fig.12.Voltage across DC-link capacitor.

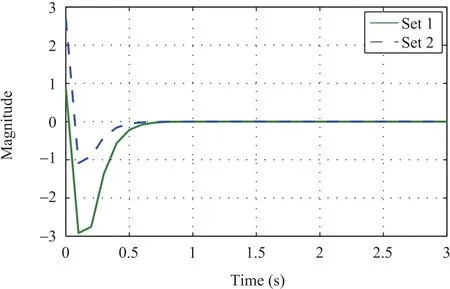
Fig.13. Inverter output current along d-axis.

Fig.14. Inverter output current along q-axis.

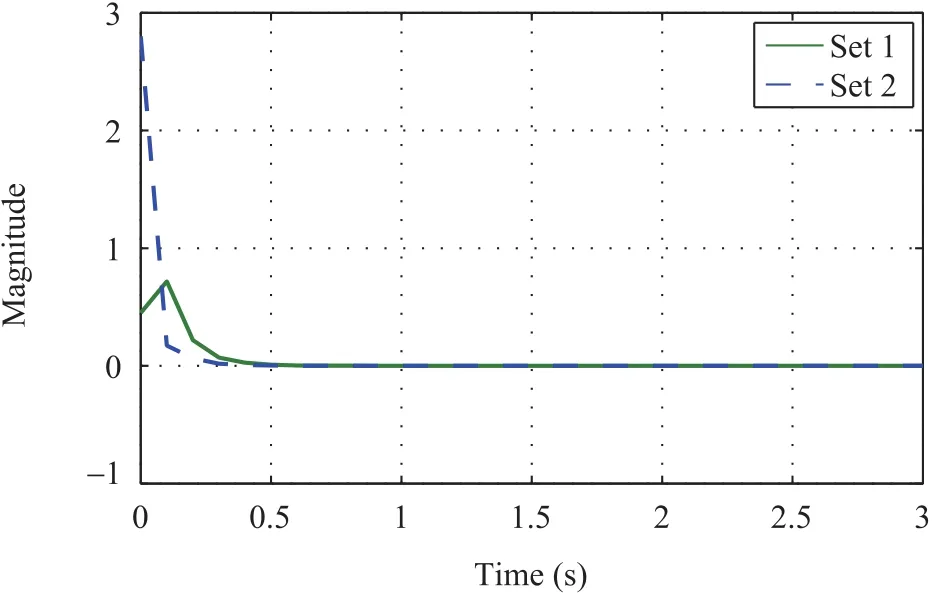
Fig.15. Coupling line current of the filter along d-axis.

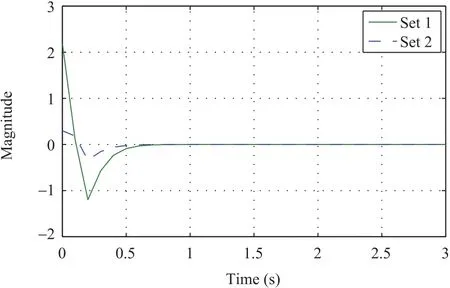
Fig.16. Coupling line current of the filter along q-axis.

Fig.17. Capacitor voltage of the filter along d-axis.

Fig.18. Capacitor voltage of the filter along q-axis.

VII.CONCLUSIONS

A networked control SoS methodology for the stabilization of a microgrid system with two sets of microalternator and PV systems are presented in this paper.The microalternator and PV system are modeled in detail.The combination of both systems connected to the main grid and a load is also modeled.The networked control system based on this model is subjected to delays and non stationary packet dropouts.An improved output feedback controller is proposed,which stabilizes the system in presence of the aforementioned communication constraints.Using pilot-scale lab equipment to build an experimental microgrid,simulation of both sets of microalternator-PV systems are attained using Matlab-Simulink environment,particularly the products Simscape Power Systems Examples.From the presented results,the effectiveness of the controller is demonstrated in solving a major issue in microgrids arising from stability of its constituent systems.

Future work would go along different avenues.One avenue would be to expand the model by including battery storage units and examine the transition between islanded and gridconnected modes of operation.Another avenue is to cast the model into a stochastic set-up by including effects of load daily as well as solar radiation variations.A final avenue is to treat the model from a multi-agent perspective and investigate various protocols.Research work along these ideas is underway.