Robust Leader-Following Output Regulation of Uncertain Multi-Agent Systems With Time-Varying Delay

Ala Shariati and Qing Zhao

Abstract—In this paper,the robust analysis and design of leader-following output regulation for multi-agent systems described by general linear models is given in presence of timevarying delay and model uncertainty.To this aim,a new regulation protocol for the closed-loop multi-agent system under a directed graph is proposed.An important specification of the proposed protocol is to guarantee the leader-following output regulation for uncertain multi-agent systems with both stable and unstable agents.Since many signals can be approximated by a combination of the stationary and ramp signals,the presented results work for adequate variety of the leaders.The analysis and design conditions are presented in terms of certain matrix inequalities.The method proposed can be used for both stationary and ramp leaders.Simulation results are presented to show the effectiveness of the proposed method.

I.INTRODUCTION

D URING the last decade,cooperative control of multiagent systems has been extensively studied due to its ever-increasing applications in many fields such as formation control,sensor network, flocking,synchronization of coupled oscillators and robot position synchronization[1]-[6].Leader following consensus problem as one of the essential problems in cooperative control has also received considerable attention in recent years.For example,Meng et al.[7]provided some analysis results for both leaderless and leader-following consensus algorithms for first-order and second-order multiagent systems in presence of communication and input delays.An LMI approach for designing a leader-following consensus protocol was also introduced for general linear multi-agent systems in presence of time-delay by Ding et al.[8]in which the leader has the same dynamics as the followers.Furthermore,for time-varying delayed first-order multi-agent systems with a static leader,leader-following consensus analysis was studied in[9]and some sufficient conditions were obtained to guarantee the convergence of the agents to the leader.A leader-following consensus problem for second-order multiagent systems with communication time-varying delays was also investigated in[10].For systems with large delay sequences,leader-following consensus problem of discrete-time multi-agent systems has been addressed in[11].Moreover,Cao et al.[12]studied the distributed containment control problem of mobile autonomous agents with multiple stationary or dynamic leaders under both fixed and switching directed network topologies.For uncertain multi-agent systems,Liu and Huang[13]addressed a leader-following consensus problem for a class of uncertain higher-order nonlinear multiagent systems in presence of external disturbances.Recently,a leader-following consensus problem has been addressed in[14]for a class of uncertain multi-agent systems with actuator faults.

In many practical leader-following multi-agent systems,the control objective is to follow a combination of the leader states as an output.This is analogous to the case that the follower agents have a virtual leader which means that there is an exo-system acting as a leader.This problem is called leader-following output regulation that has attracted attention in recent years[15]-[18].Therefore,the problem of leaderfollowing output consensus can be viewed as the special case of cooperative output regulation problem.In[15],an algorithm for designing a distributed control law is provided for a robust cooperative control of multi-agent system with distributed output regulation.Yan and Huang[16]addressed the analysis of a cooperative output regulation for linear timedelay multi-agent systems.Moreover,a cooperative output regulation analysis of heterogeneous multi-agent systems is carried out in[17].To the best of our knowledge,very few works have focused on output regulation problem of multi-agent systems with time-delay.Recently,a descriptor approach to robust leader-following output regulation design of multi-agent systems was given in[19]in the presence of both uncertainty and constant transmission delay.The presented method in this study works for both stable and unstable agents.Furthermore,Yan and Huang[18]addressed the cooperative robust output regulation problem for a discretetime linear time-delay multi agent systems with stable agents.Since,the presented output regulation methods in the literature for time-delay multi-agent systems cannot handle the timevarying delays,we are motivated to investigate a robust leaderfollowing output regulation for uncertain general linear multiagent systems with stationary and ramp-type dynamic leaders as well as both stable and unstable agents in presence of timevarying delay.The contributions of this paper are summarized as follows:

1)A new regulation protocol is proposed in this paper that works for both stationary and ramp-type dynamic leaders.

2)Applying this protocol,a time-delay closed-loop system of retarded type is obtained that is simpler to deal with than the closed-loop system of neutral type presented in[19].

3)Using direct Lyapunov-Krasovskii method,robust analysis and design conditions for the leader-following output regulation of uncertain multi-agent systems with transmission timevarying delay are given in terms of linear matrix inequalities.The derived LMI conditions have smaller dimensions than the ones obtained in[19].

4)As mentioned,in this paper,a time-varying transmission delay is assumed in leader-following multi-agent system whereas the studies in[18]and[19]are based on a constant time-delay.Furthermore,our method can deal with both stable and unstable agents.

This paper is organized as follows.Problem formulation and preliminary results as well as a new regulation protocol are given in Section II.In Section III,The robust stability analysis conditions are provided in terms of certain linear matrix inequalities.Moreover,the design conditions are given in Section IV.Some illustrative examples are provided in Section V to show the effectiveness of the proposed methods.Finally,the concluding remarks are given in Section VI.

Notations:R denotes the real number field.Rm×mdenotes the set of all m×m dimensional real matrices.Imdenotes m×m dimensional identity matrices and⊗ denotes the Kronecker product.For a given real vector or matrix X,XTdenotes its transpose and‖X‖denotes its Euclidean norm.For a square nonsingular matrix X,X-1denotes its inverse matrix.Throughout the paper,the notations ΔA and ΔB are used for ΔA(t)and ΔB(t)in some of the equations for the sake of brevity.

II.PRELIMINARIES AND PROBLEM STATEMENT

A.Graph Theory

Let G=(V,E,A)be a digraph with the set of vertices V={1,2,...,N}and the set of edges E⊆V×V.In G,the i th vertex represents the i th agent.The adjacency matrix A=[aij]∈ RN×Nrepresents the communication topology among the agents in which aii=0,aij＞0 if the j th agent is a neighbor of the i th agent,otherwise aij=0.The degree matrix of graph G is denoted by D=diag{d1,d2,...,dN},in whichCorrespondingly,the Laplacian matrix of the directed graph G is defined as Ls=D-A.In a directed edge,the information flows from the agent i to the agent j and is represented as a pair(i,j)∈E.A sequence of directed edges is called directed path in which the edges all are in the same direction.A digraph is called connected if there is a directed path between every pair of vertices.

B.Multi-Agent System Structure and Formulation

Consider a group of N uncertain n th order agents represented by the following linear differential equation for each agent:

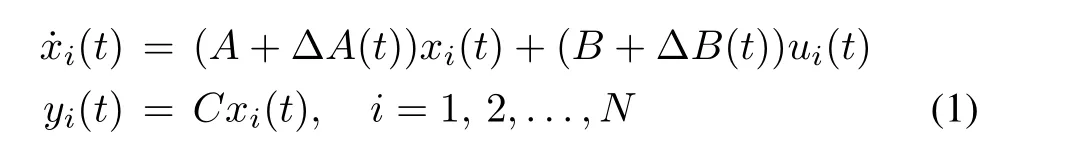
where xi(t)∈Rn,ui(t)∈Rm,yi(t)∈Rrare respectively the agent i’s state,input and output,respectively,which can only use the local information from its neighbor agents.Moreover,the constant matrices A ∈ Rn×n,B ∈ Rn×mand C ∈ Rr×nrepresent the identical nominal dynamics and ΔA(t)and ΔB(t)are real matrix functions representing timevarying parameter uncertainties.These uncertainties are the result of model linearization and unmodeled dynamics.These admissible uncertainties are assumed to be of the form

where Fa(t)and Fb(t)are unknown real time-varying matrices with Lebesgue measurable elements satisfying

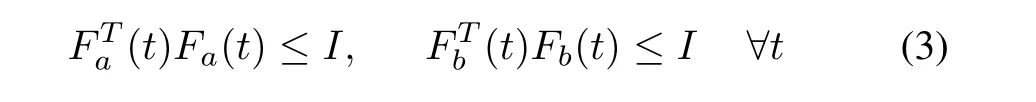
and Da,Ea,Db,Ebare real known constant matrices which represent how the uncertain parameters in Fa(t)and Fb(t)enter the nominal matrices A and B.

In this paper we consider the design of an appropriate feedback control ui(t),i=1,...,N to render all the follower agents’output to asymptotically follow the leader.This is stated by the following definition.

Definition 1:For any initial condition yi(0)and the leader y0(t),the leader-following output regulation is achieved if there exists a local feedback control ui(t)for each agent such that the closed-loop system satisfies

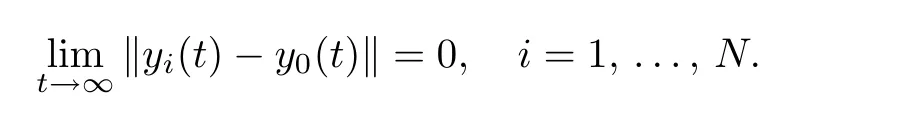
The control objective of the leader-following output regulation of a multi-agent system is to follow the output of a real or virtual leader.This output plays the role of a set-point for the followers.Moreover,in many practical problems,the leader has its own feedback independent of the followers in order to obtain the appropriate set-point in its output for the followers.Therefore,we find that in a general case,the model of the followers and the leader can be non-identical.On the other hand,in practice,many of the desired outputs of the agents can be approximated by stationary or ramp signals.Hence,we focus on designing leader-following output regulation of the uncertain multi-agent systems for stationary and ramp-type dynamic leaders in this paper.These leaders are labeled as i=0 and considered by the following representations:

where y0(t)∈Rris the output of the leader and a0,r0∈R.The leaders introduced in(4)and(5)refer to stationary and ramp-type dynamic leaders respectively that should be followed by all the follower agents.The network topology of the multi-agent system is shown in Fig.1.In this topology,it is assumed that N0number of the agents(0＜N0≤N)have access to the leader.These agents are named as“reference followers”.Moreover,we assume that the reference followers have a limited computational capability and no computation or processing is carried out in the rest of the followers.Together with the reference followers,the leader can also perform required computations in the network of the multiagent system.Let τr(t)be the data transmission delay from the leader to the reference followers and τs(t)be the delay of transmitting data from the reference followers to the leader.It is supposed that the data transmission delay between the follower agents is negligible.

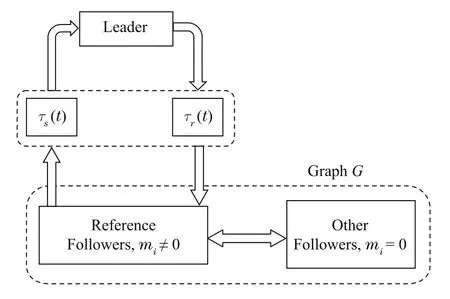
Fig.1.Network topology of the directed multi-agent system.

Now,we state the following assumptions that are needed throughout the paper.

Assumption 1:The graph G is fixed and directed.

Assumption 2:The pair(A,B)is stabilizable and the pair(A,C)is detectable.

Assumption 3:The digraph G is strongly connected.

C.Leader-Following Regulation Protocol

To deal with the leaders(4)and(5)in the network of multi-agent system presented in Fig.1,we propose a new consensus protocol for system(1)in presence of transmission delay shown in a general form that works for both stationary and dynamic leaders(4)and(5)as

in which

with τ(t)=τr(t)+τs(t),0≤τ(t)＜˙τ,0≤|˙τ(t)|＜λ,0≤τr(t)＜ τrand 0≤τs(t)＜ τs,where τ= τr+ τs.

As seen in(6),the proposed regulation protocol is composed of two parts:consensus(uiC(t))and tracking(uiT(t)).Obviously,the reference followers receive both consensus and tracking parts as mi/=0 whereas the rest of the followers merely receive the consensus part(uiC(t))of the protocol(6).Furthermore,we assume that the tracking part of the regulation protocol is computed in the reference followers.This is why apart from the induced transmission delay τr(t)in the leader signal,no other transmission delay is induced in the tracking part of the protocol(6).We further assume that uiC(t)is computed in the leader and is distributed among the followers through the reference followers.Thus,both delays τr(t)and τs(t)are induced in the consensus part of the protocol(6).Furthermore,K,KI,KII,,,∈ Rm×rare feedback matrices to be designed and miis a scalar that is 1 if the agent i is the neighbor of the leader and 0 otherwise.As seen in(6),different controller gainsare considered for different agents.This strategy leads to more flexibility in design and less conservatism in the result.Applying the consensus protocol(6)to the system(1),the closed-loop system equation for the agent i is represented as

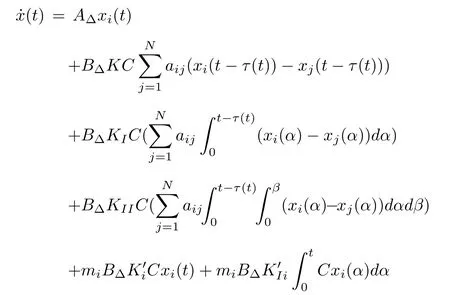
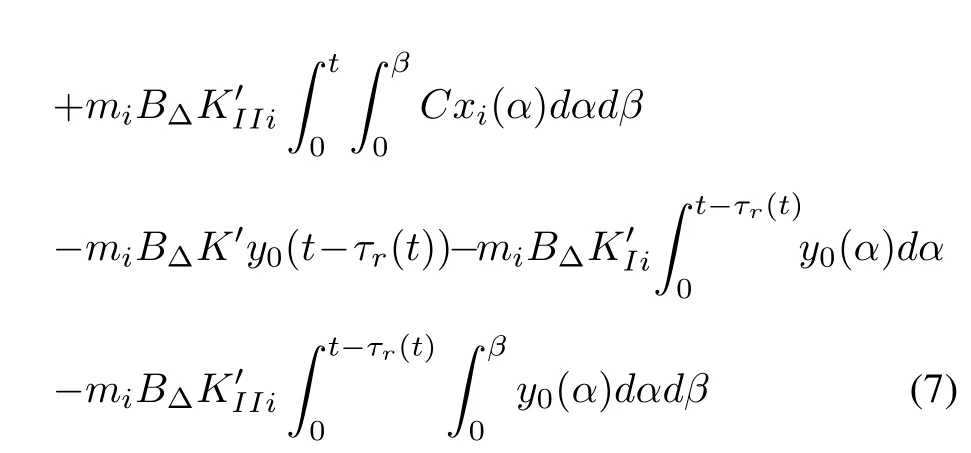
with AΔ=A+ΔA and BΔ=B+ΔB.Moreover,y0(t)=r0and y0(t)=r0t are respectively considered for the leaders(4)and(5).Then,the network dynamics of the multi-agent system is represented as

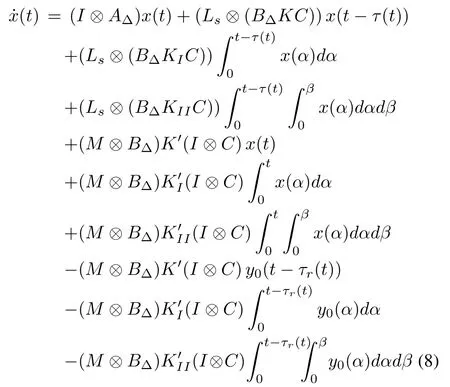
Lsis the Laplacian matrix,x(t)=

K0=diag= diag{,...,K2N},M=diag{m1,...,mN}.

Remark 1:It is well-known that a Proportional-Integral(PI)or Proportional-Integral-Double integral(PII2)controller designed for a stabilization problem can be further used for tracking problem of the same closed-loop system.Therefore,the leader-following output regulation of the system(8)is guaranteed as long as the stability of the following system is satisfied.

Remark 2:The simple and double integrator statements in(6)play important roles in achieving a general condition for the robust leader-following output regulation of the uncertain multi-agent systems with general linear dynamics in presence of each of the leaders(4)and(5).In other words,these integrators provide output tracking of a closed-loop multiagent system for stationary or ramp-type dynamic leader that can prevalently occur in practice.

Now,we consider(9)and define new variables η(t)=Then,the state space equation of the multi-agent system is represented as follows:

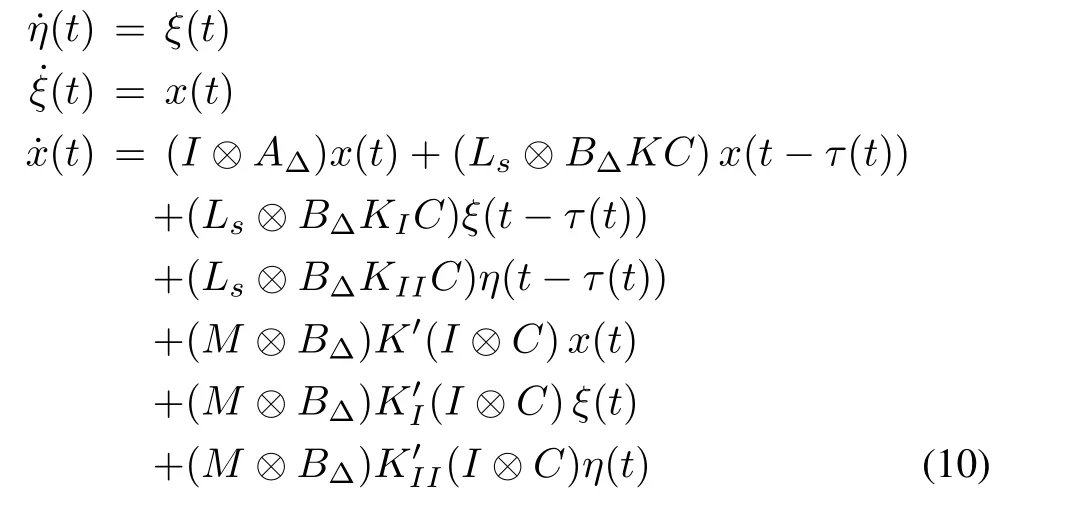
or

where

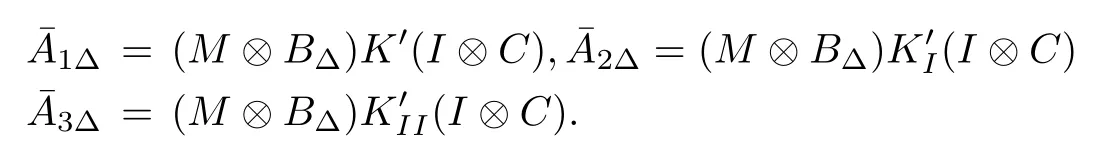
Now,we present the following lemmas which will be used in the main results of the paper.

Lemma 1[20]:Let H,L and F(t)be real matrices of appropriate dimensions with F(t)being a matrix function.Then,for any σ ＞ 0 and FT(t)F(t)≤ I,we have

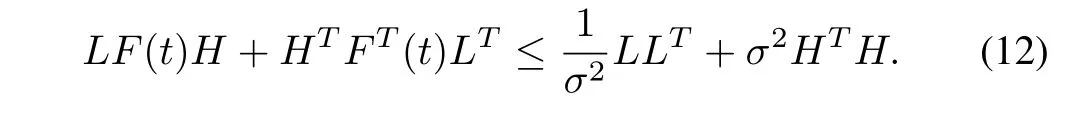
Lemma 2[21]:If W＞0,there exist W-1.Thus,

For the sake of brevity,the proofs of these two lemmas are omitted.

III.ROBUST STABILITY OF LEADER-FOLLOWING OUTPUT REGULATION

In this section,we concentrate on deriving a robust stability analysis criterion for leader-following output regulation of uncertain time-delay multi-agent system(10).Defining

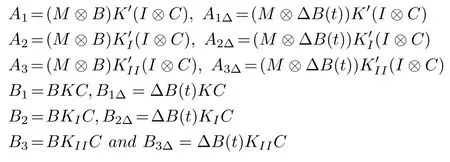
in(10),we will have

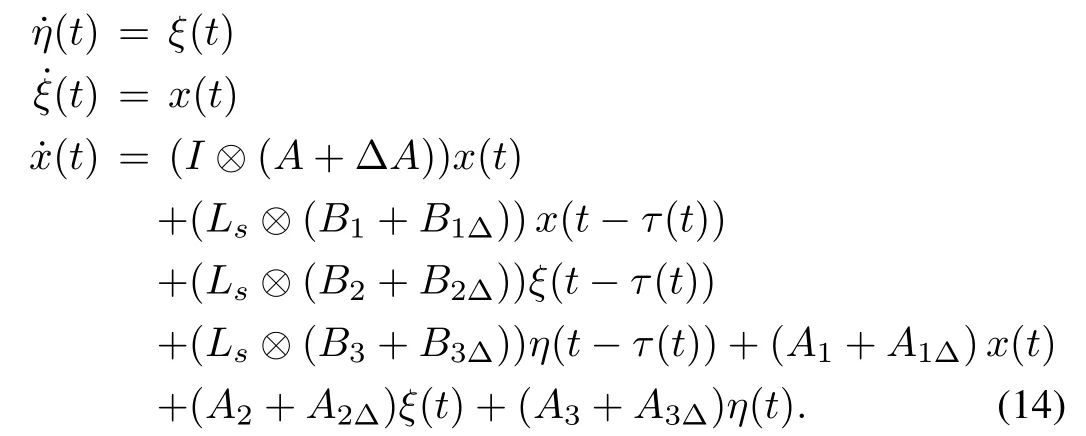
A Lyapunov-Krasovskii functional for system(14)has the form

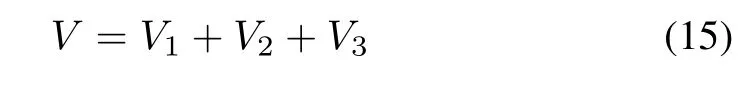
where

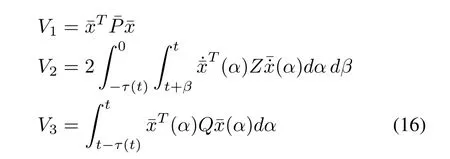
Theorem 1:Under Assumptions 1-3,for given time-delay τ(t)with 0≤τ(t)＜ τ and 0≤|˙τ(t)|＜λ,the system(14)is asymptotically stable if there exist scalars σ1,2,i=1,2,3,positive definite symmetric matrices P,X,Q,Z∈R3nN×3nNand matrix Y ∈R3nN×3nNsatisfying the following LMIs:

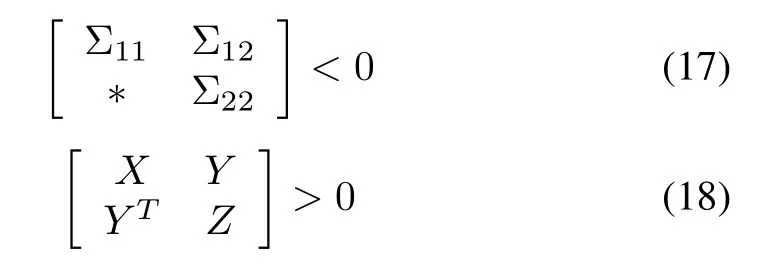
in which

Proof:Using Lyapunov-Krasovskii functional in(15)and(16),the delay-dependent sufficient conditions for the stability of the delayed multi-agent system(14)are presented.For sake of brevity,the detailed proof of this theorem is given in Appendix.

Remark 3:Theorem 1 provides robust stability analysis conditions for uncertain multi-agent system(14).Feasibility of the set of LMI conditions(17)and(18)guarantees the robust leader-following output regulation of the uncertain time-delay multi-agent system(14)with known state-space matrices.The significant advantage of this theorem is to give a set of stability analysis LMI conditions that are valid for both leaders(4)and(5).

Remark 4:It is worthwhile mentioning that the proposed leader-following output regulation protocol can be further used for low frequency sinusoidal leaders or the leaders that can be approximated by a combination of a number of sinusoidal signals.The tracking quality for high frequency sinusoidal leaders can be improved by incorporating a design criterion for widening the bandwidth of the closed-loop system.

Remark 5:In non-time-delay case,all the rows and columns containing τ are omitted from the LMI conditions(17)and(18).Therefore,some less complicated LMI conditions are provided for this case.These delay free LMI conditions are also obtained by considering the state-space equation of the closed-loop multi-agent system with τ(t)=0 and the Lyapunov function as V(t)= xT(t) P x(t).All the proof procedure is given in the appendix.

IV.DESIGN OF ROBUST LEADER-FOLLOWING OUTPUT REGULATION CONTROL

In this section,using the analysis conditions provided in the previous section as well as the preliminaries given in the Section II,design conditions for the proposed leaderfollowing output regulation control are given.These conditions are presented by the following theorem.

Theorem 2:Consider the multi-agent system(1)and the control law(6)with time-varying transmission delay τ(t)that 0≤τ(t)＜ τ and 0≤|τ(t)|＜λ.Suppose Assumptions 1-3 are satisfied.The leader-following output regulation is asymptotically achieved for the leaders(4)and(5)if there exist scalars ε, σ1,2, αi＞ 0,i=1,2,3,positive definite symmetric matrices L,T1,T2R∈R3nN×3nN,matrix N∈R3nN×3nN,matrices K0,K0I,K0II∈ RmN×rNand scalars K,KI,KIIsatisfying the following matrix inequalities:

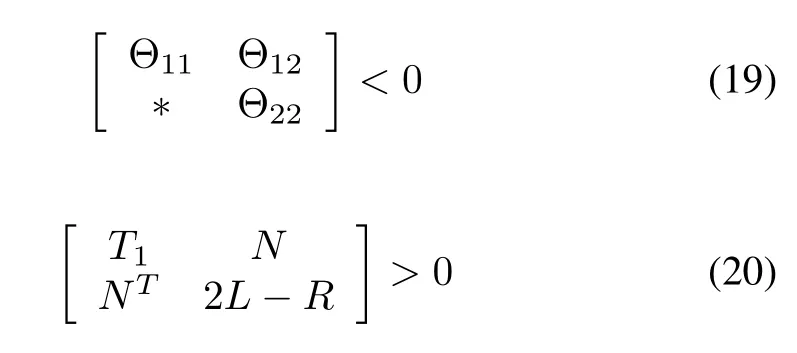
in which

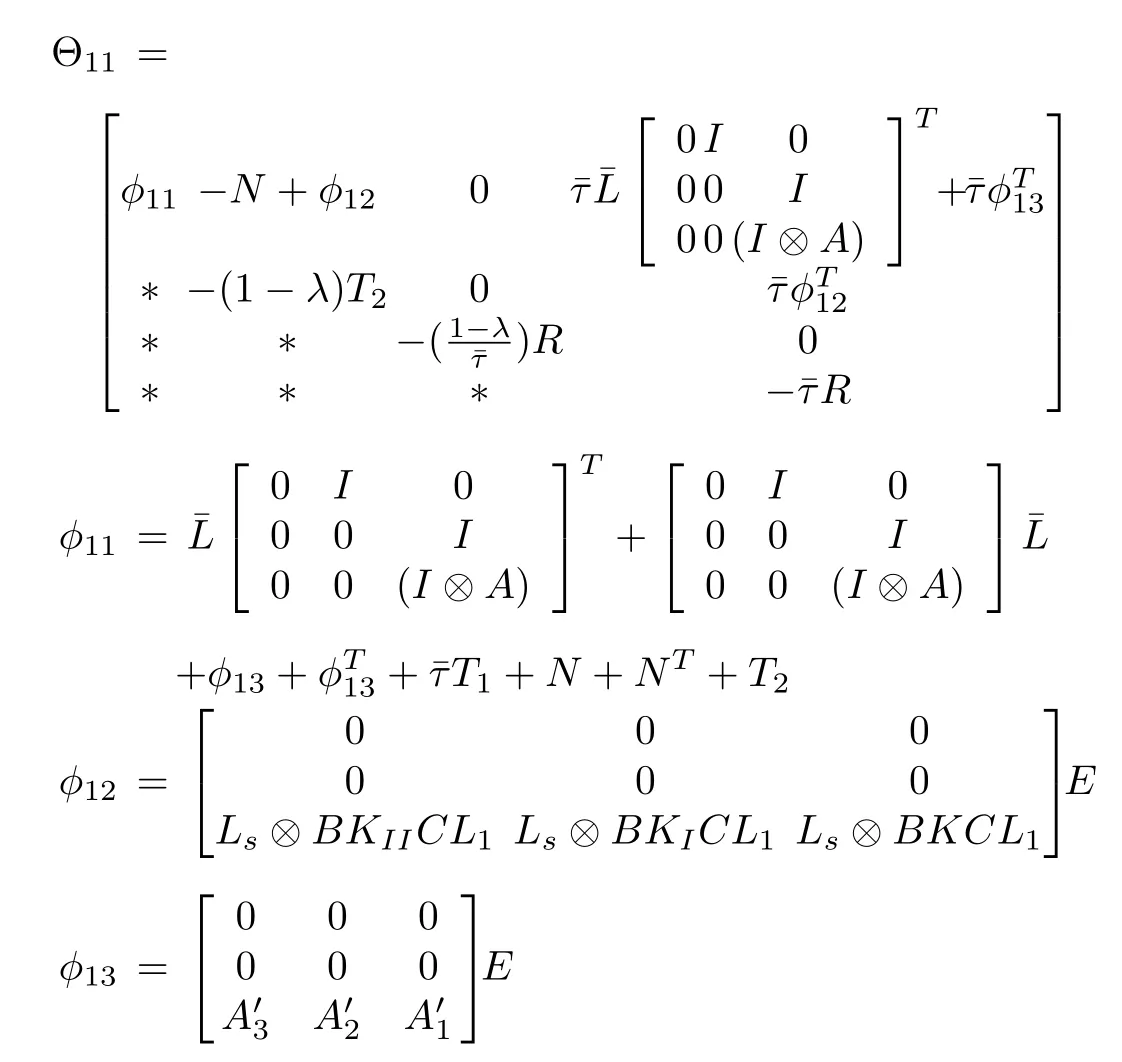
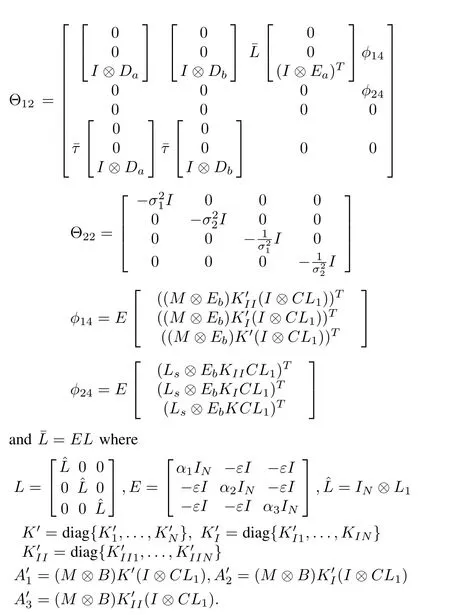
Proof:See Appendix.

Remark 6:As we mentioned earlier,Theorem 1 gives a general set of matrix inequality conditions for stability analysis and design of leader-following output regulation of multi-agent system(1)with regulation protocol(8).Solving the presented conditions in(19)and(20),we obtain the appropriate solution for the regulation protocol(8)that works for each of the leaders(4)and(5).In a special case that the stationary leader is merely considered,one can set KII=KIIi=0 and derive a set of simpler stability analysis and design conditions than the general form.This special case will lead to the regulation protocol(21)that is a sub-case of the regulation protocol(7).

Then,the following corollary is obtained.

Corollary 1:Under Assumptions 1-3,the leader-following output regulation is asymptotically achieved for the multiagent system(1)with 0≤τ(t)＜ τ,0≤|˙τ(t)|＜λ and the control law(21)in presence of stationary leaders,if there exist scalars ε,σ1,σ2＞ 0,positive definite symmetric matrices L,T1,T2,R∈R2nN×2nN,matrix N∈R2nN×2nNand matrices K,KI,K0,K0I∈ Rm×rsatisfying the following matrix inequalities:

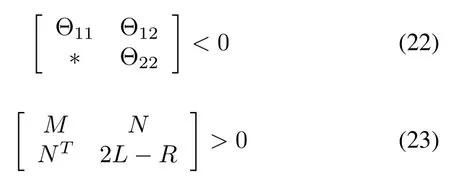
in which

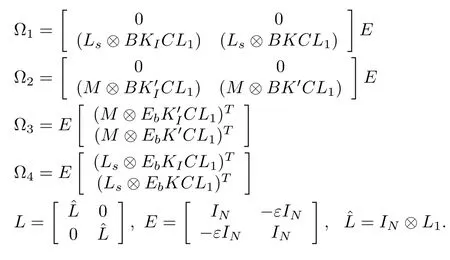
Proof:The proof is omitted since it can be directly established using Theorem 2.

Remark 7:As seen in the leader-following conditions presented in Theorem 2 and Corollary 1,the matrix inequalities(19)and(22)are bilinear(BMI).Although BMIs are categorized in NP-hard problems,there exist practically effective algorithms for BMI solutions[22],[23].Furthermore,the PENBMI solver in MATLAB environment can be used to solve BMIs[24].It is noteworthy that for the first-order systems as a special case,the obtained BMI condition in(19)and(22)turn into LMI that are much easier to deal with as compared to BMIs.The details are given as follows.

A.Special Case:First-Order Systems

Consider the following first-order system:

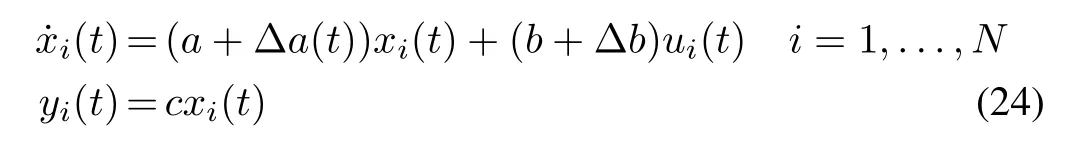
where a,Δa,b,Δb and c are scalars.Replacing A=a,B=b,ΔA(t)= Δa(t)and ΔB(t)= Δb(t),the BMI terms in the matrix inequalities(22)and(23)obtained in Theorem 2 can be written asDefiningthe matrix inequalities(22)and(23)turn into LMI.Moreover,the controller gains are given byfor i=1,2,3.A similar procedure can be used for the results provided in Corollary 1 in order to obtain LMI design conditions for the leaderfollowing output regulation problem for the stationary leaders.Thus,it is omitted here.

V.SIMULATION

In this section,two examples are given to illustrate the effectiveness of the theoretical results.

A.Example 1

In this example,we consider two multi-agent systems I and II with six uncertain first-order agents as follows:

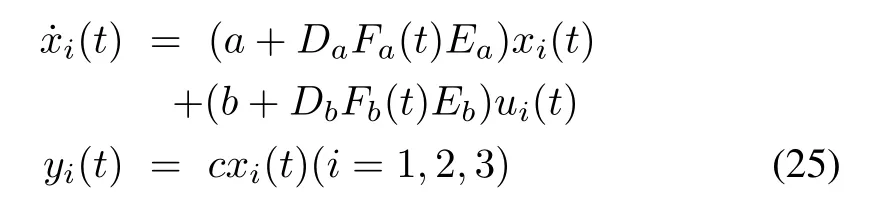
The agents in system I are stable in which a=-5,b=5,c=1,Da=0.15,Db=0.1,Ea=1,Eb=1 with a time-delay bound=180 ms and=20 ms.For system II,the agents are unstable with a=1.1,b=6,c=1,Da=0.1,Db=0.05,Ea=1,Eb=1,with a time-delay bound=70 ms and=20 ms.In both systems I and II,we have(t)Fa(t)＜ 1,(t)Fb(t)＜ 1.The communication topology is represented by the Laplacian matrix Ls=[lij]for i,j=1,2,...,6 where lii=1 for i=1,2,...,6 and l12=l23=l34=l45=l56=l61=1,otherwise lij=0 for i=1,2,...,6.Furthermore,the leader adjacency matrix M is given as M =diag{1,0,1,0,1,0}.We set ε=0.2,α1=α3=1,α2=0.25,σ1=σ2=1.Using Theorem 2 and the results presented in Section IV-A.as well as LMI Toolbox in MATLAB,the designed controllers are obtained for the multi-agent system I as

and the multi-agent system II as

Two set points ramp and sinusoidal are applied to the agent 1 and 2 as the state of the leader.Figs.2-5 display the simulation results of the multi-agent systems I and II.The initial conditions for the agents 1,2,...,6 are considered as 0.5,2,-1,1,-0.8,-2 and 3,2,-1,2.5,-1.5,-2 for systems I and II,respectively.

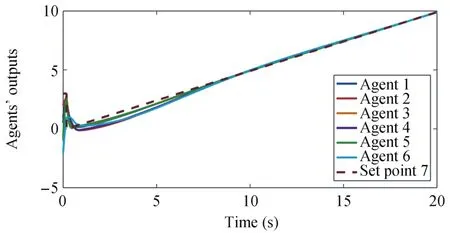
Fig.2.Controlled outputs of the follower agents(solid)and output of the leader(dashed)in system I.

Fig.3.Controlled outputs of the follower agents(solid)and output of the leader(dashed)in system I.

Fig.4.Controlled outputs of the follower agents(solid)and output of the leader(dashed)in system II.

Fig.5.Controlled outputs of the follower agents(solid)and output of the leader(dashed)in system II.

As seen in Figs.2 and 3,a leader-following output regulation is achieved for multi-agent system I and the agents’outputs follow a ramp path as well as sinusoidal path using the regulation protocol(6).Moreover,the unstable multiagent system II has been stabilized and the leader-following output regulation is obtained as seen in Figs.4 and 5.These simulation results show that the proposed method can be used for the leader-following output regulation problems with hyperbolic leaders as well.Furthermore,as expected,the presented method provides leader-following output regulation for multi-agent systems in which the followers do not have necessarily the same dynamics as their leader.

B.Example 2

In this example,we address the problem of the robust stability analysis of the leader-following output regulation for multi-agent systems investigated in Section III.To this aim,we consider equation(1)with the following state-space matrices of an unstable nominal multi-agent system:

The communication topology and the leader adjacency matrices are represented asand M=diag{1,0,1},respectively.Furthermore,considering the dynamic leader(5)and the regulation protocol(6),the controller gains are assumed as follows:

Now,Theorem 1 can be applied for the stability analysis of the closed-loop system in presence of delay.For this purpose,we use the LMI Toolbox in MATLAB and solve the LMI conditions(17)and(18)with τ=20 ms and τr=10 ms.Simulation results show that these LMI conditions are feasible.It means that the regulation protocol(6)with the controller gains(27)stabilizes the closed-loop multi-agent system for the leader(5)in the presence of τ=20 ms.We set a step leader r=2 for the first output and a ramp-type leader with a slope of 1 for the second output.Furthermore,we assume that the initial conditions of the agents’state variables are 0.1,0.2,0 for the agents 1-3 respectively.The leader-following output regulation of the closed-loop multi-agent system is achieved as shown in Figs.6 and 7.

Now,we perform some simulations in order to examine the robust stability of the closed-loop system in the presence of system parameter variations.Since the stability of the closed-loop system is affected by the uncertainty in timedelay,gain and poles of the open-loop system,we investigate the performance of the closed-loop system in the presence of these uncertainties.To this aim,we set ΔA=0,ΔB=0 and increase τ while repeating simulation.The simulation results show that the LMI conditions(17)and(18)are feasible for the maximum time-delay τmax=77 ms.This means that the stability of the closed-loop multi-agent system is guaranteed for all delays τ(t) ≤ 77 ms with ΔA=0,ΔB=0.Now,we set ΔA=0 and define ΔB= αB.Then,solving the LMI conditions(17)and(18)in presence of the variations of α and τ,the feasibility region for these LMI conditions is obtained as shown in Fig.8.Therefore,the colored area in Fig.8 shows the guaranteed stability region for the closed-loop multi-agent system for the variations of τ and ΔB with ΔA=0.Since the variations of ΔB directly affects the gain of the closedloop multi-agent system,it is reasonable to observe that the closed-loop multi-agent system is stable for ΔB ≥ -0.83B where ΔA=0, τ=0.To see the stability region of the closed-loop multi-agent system in presence of the uncertainty on the poles of the system(26)that are at λ1,2=0.5±3.1225i,we set ΔB=0.Then,varying the real part of the poles of the system(26)gives the range ΔRe(λi) ≤ 5.05,i=1,2 for the feasibility of the LMI conditions(17)and(18).As seen in Fig.9,increasing the maximum time-delay τ leads to decreasing the upper limit of the real part uncertainty of the system poles.

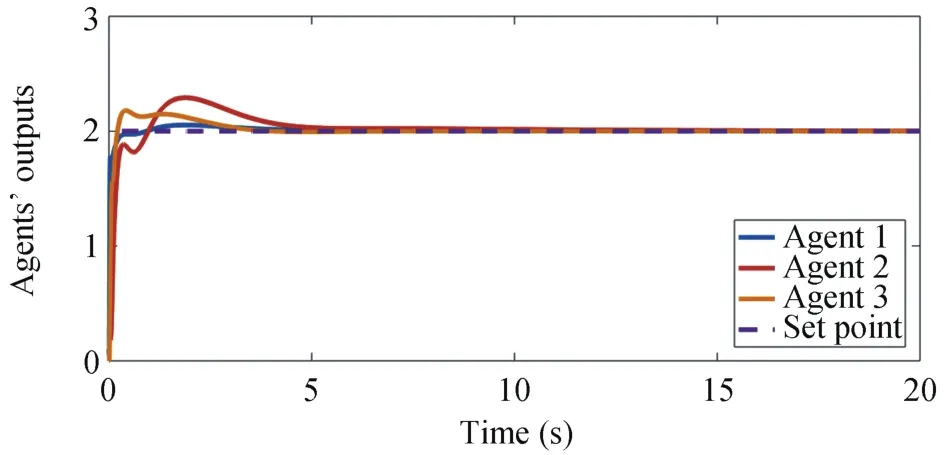
Fig.6.First controlled outputs of the follower agents(solid)and output of the leader(dashed).

Fig.7.Second controlled outputs of the follower agents(solid)and output of the leader(dashed).

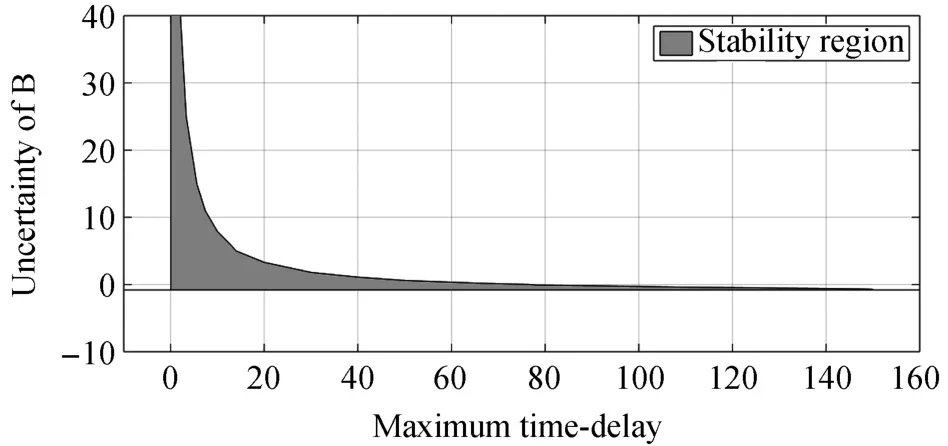
Fig.8.Stability region in presence of and ΔB variations when ΔA=0.

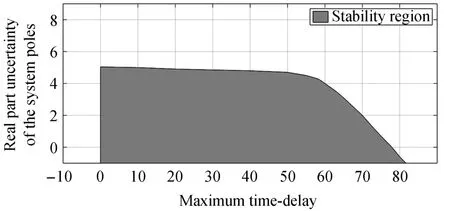
Fig.9.Stability region in presence of τ and ΔA variations due to real part variations of λ1,2 when ΔB=0.

VI.CONCLUSION

The problem of leader-following output regulation analysis and design of uncertain general linear multi-agent systems with transmission delay has been presented in this paper.The proposed method can be used for both stable and unstable follower agents under a directed graph.Many of the leader outputs can be approximated by the stationary and ramp signals.Therefore,two stationary and ramp-type dynamic leaders have been investigated in this paper that cover adequate variety of the leaders.To this aim,we proposed a new regulation protocol for the closed-loop system.The analysis conditions have been presented in terms of certain LMIs in which the provided results for design purposes are bilinear.It was shown that for first-order systems as special case,the presented results are turned into LMI.Finally,we presented two analysis and design examples for the leader-following output regulation of time-delay uncertain multi-agent systems.We showed that our proposed method effectively meets the quality requirements of the leader-following output regulation for both stationary and dynamic leaders.Moreover,we showed that this method can be further used in presence of low-frequency sinusoidal leaders.To achieve superior leader-following output regulation for high-frequency sinusoidal leaders,the bandwidth of the closed-loop system should be widened.To this aim,an appropriate performance objective is required to be added to the stability criterion that can be considered in the future works.

APPENDIX

Proof of Theorem 1:Differentiating V1in(16)with respect to t and using the integral inequality in[25],results into

with

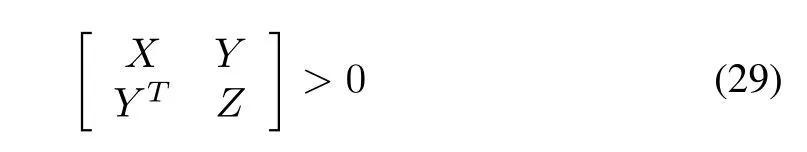
where

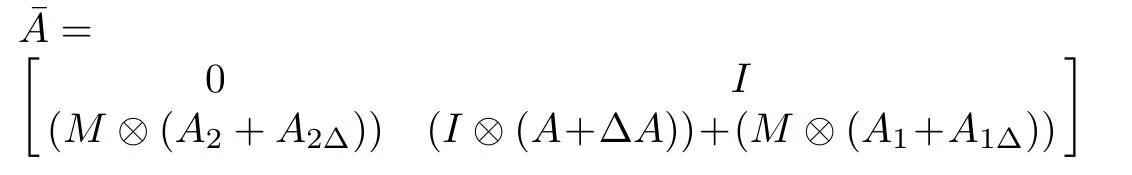
and

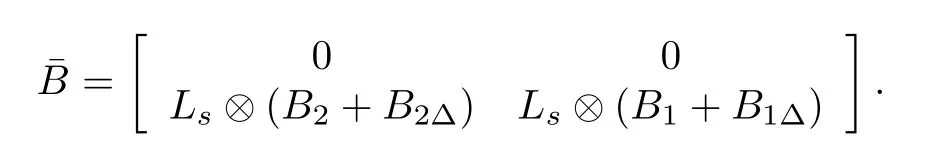
Also,the time-derivative of V2and V3can be represented as follow

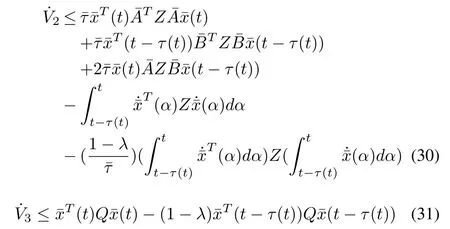
in which

If the condition Θ＜0 holds,the negative definiteness of˙V(t)is guaranteed and asymptotic stability of the system(10)is established.Using Schur complement on Θ＜0 the following matrix inequalities are obtained

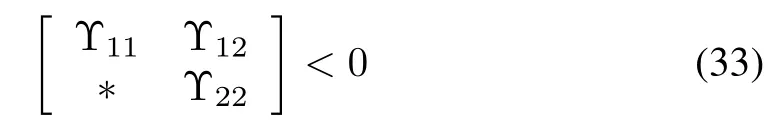
in which

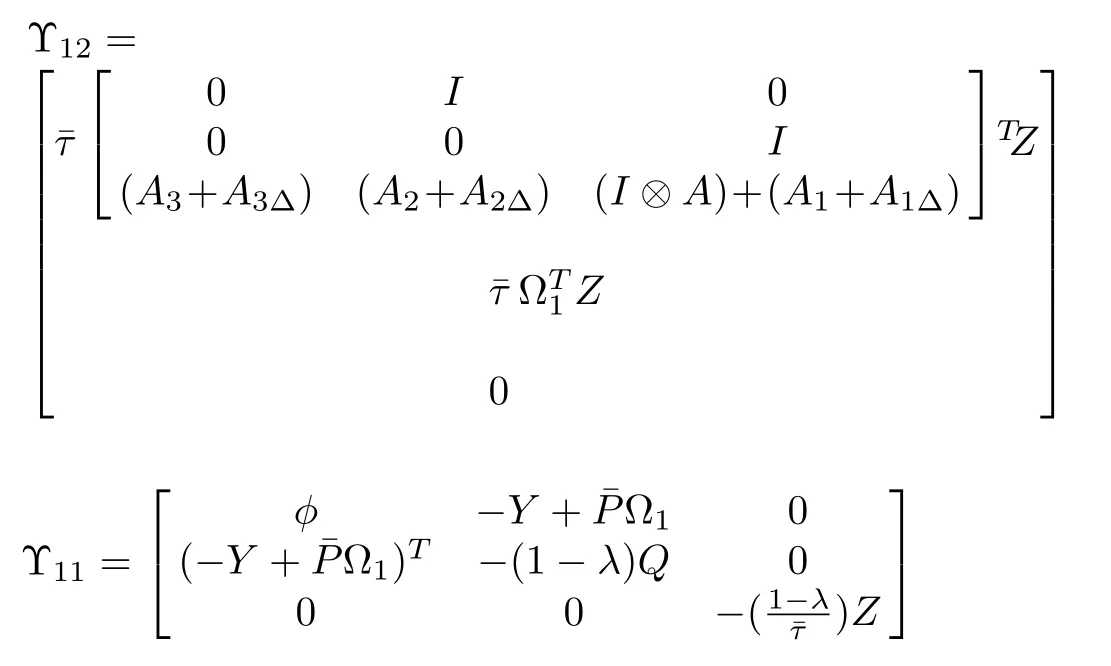
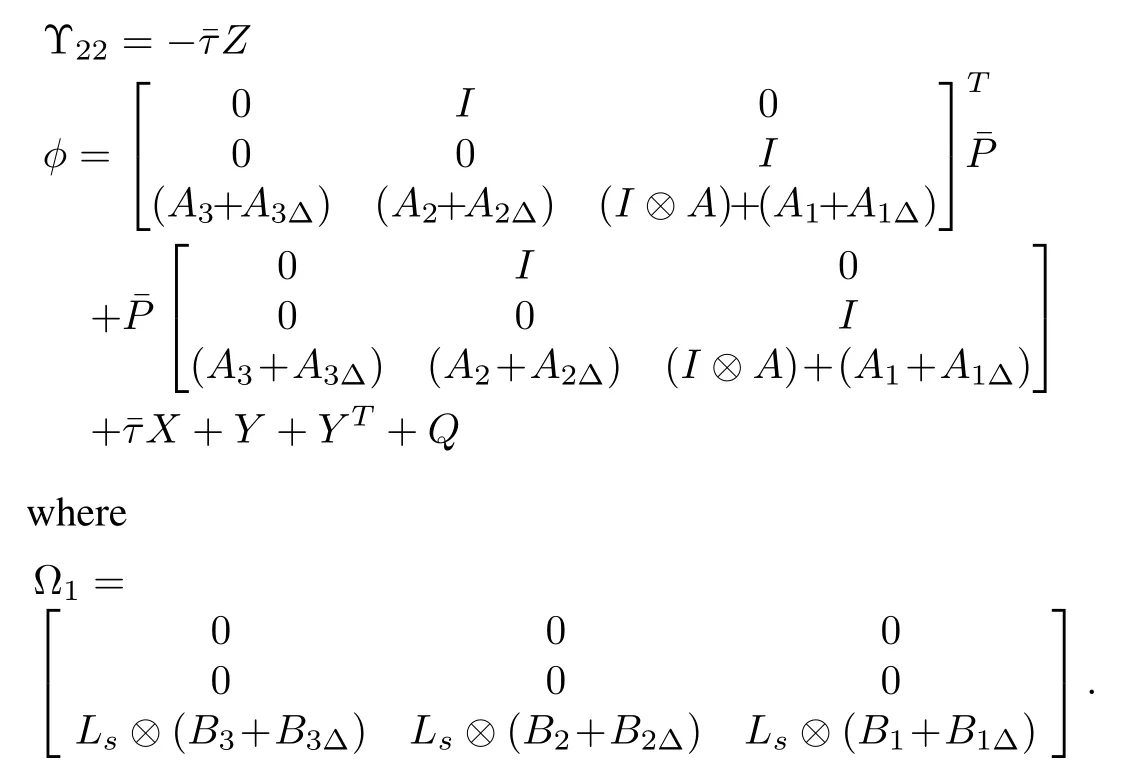
Partitioning the nominal and uncertain parts in(33)and considering the definitions in(2),we have

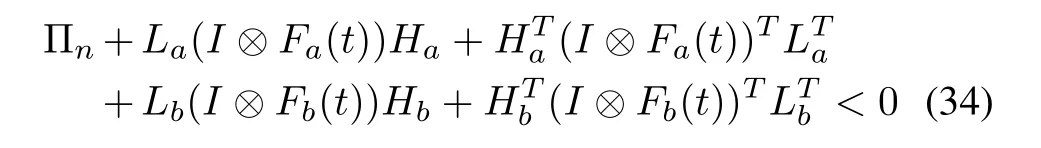
where

Since the conditions in(3)are satisfied,it can be easily shown that

Therefore,using Lemma 1,the inequality(34)is written as

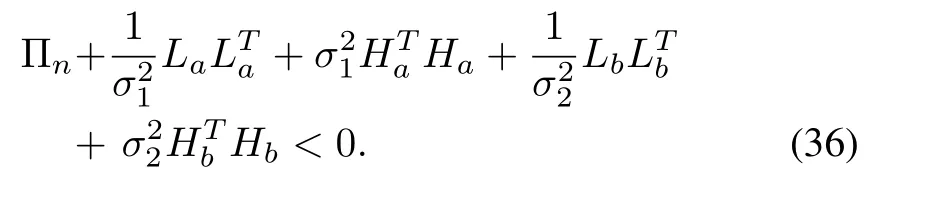
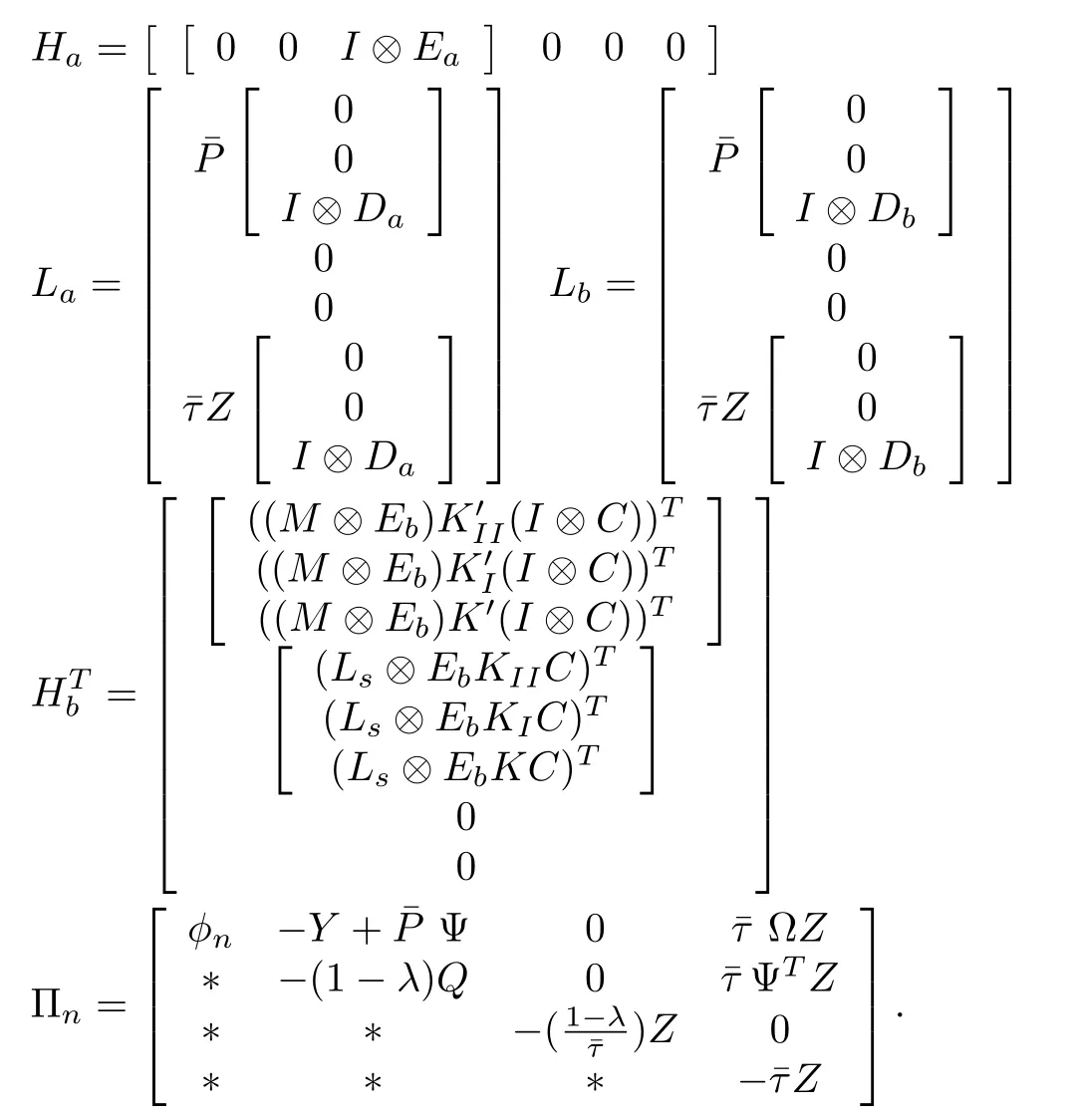
Applying Schur complement and considering(29),the matrix inequalities(17)and(18)are obtained.

Proof of Theorem 2:Pre and post multiplying the matrix inequality(17)by diagas well as defining

in which L=E L

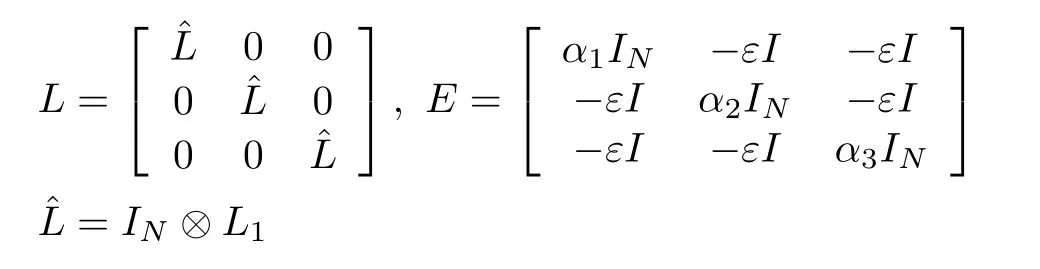
the matrix inequality(22)is obtained.Furthermore,Pre and post multiplying the matrix inequality(29)by diagand using Lemma 2,the matrix inequality(23)is also obtained.