Analysis of the Caratheodory’s Theorem on Dynamical System Trajectories Under Numerical Uncertainty

Pavel Osinenko,Grigory Devadze,and Stefan Streif,Member,IEEE

Abstract—The current work proposes a new and constructive proof for the Caratheodory’s theorem on existence and uniqueness of trajectories of dynamical systems.The key concern is the numerical uncertainty,i.e.,the discrepancy between mathematical proofs,algorithms,and their implementations,which may affect the correct functioning of a control system.Due to growing demands on security and compliance with specifications,correctness of the control system functioning is becoming ever more important.Since in both dynamical systems and many control design approaches,one of the central notions is the system trajectory,it is important to address existence and uniqueness of system trajectories in a way which incorporates numerical uncertainty.Constructive analysis is a particular approach to formalizing numerical uncertainty and is used as the basis of the current work.The major difficulties of guaranteeing existence and uniqueness of system trajectories arise in the case of systems and controllers which possess discontinuities in time,since classical solutions to initial value problems do not exist.This issue is addressed in Caratheodory’s theorem.A particular constructive variant of the theorem is proven which covers a large class of problems found in practice.

I.INTRODUCTION

M ANY analyses of controllers and associated proofs rely on existence and uniqueness of system trajectories in continuous time.A large class of control systems possess discontinuities in time which oftentimes complicates the analysis.Particular examples include step response,event-triggered systems and optimal control where time-discontinuous control laws are typical.For some of the recent applications,where the discussed phenomenon arises[1]-[3].Consider,for instance,the problem of optimal control of a vibrating spring with an attached unit mass described by the differential equation

where x is the vertical displacement and u is an external applied force.By Pontryagin’s maximum principle[4],it can be shown that an optimal force control,that brings the spring to a rest in minimum time,has the form

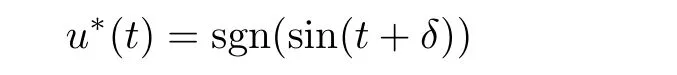
for a certain parameter δ.This is a time-discontinuous signal with switching each π units of time.

Consider now the problem of maximizing the number of queens in an ant colony.The dynamics can be described as follows:

where w,q are the number of workers and queens respectively,a,b＞0 are parameters,and u describes the proportion of the workers’effort between producing more workers or queens.It can be shown that an optimal strategy has the form

In such examples,the right-hand side of the system dynamics becomes discontinuous in time and classical system trajectories do not exist(they may,however,exist in the so called extended sense,or Caratheodory sense,which will be discussed further).In practice,the optimal controller u∗is usually implemented in a digital computational device which has a finite precision and computation speed.It may also happen that u∗needs to be discontinuous in time,e.g.needs to switch between some fixed values,to achieve optimality.In a computational device,such switchings in general may not take place arbitrarily fast,i.e.,be arbitrarily close to each other.Furthermore,the switching times are in general described by some real numbers.In a computational device,they are usually approximated by rational numbers.Such a discrepancy between the idealistic u∗and its representation in a computational device may be indicated as numerical uncertainty.The current work is motivated by the presence of numerical uncertainty in implementations and to investigate under which conditions,Caratheodory solutions may be effectively constructed,i.e.,with discontinuities in time and up to any prescribed precision.The proof of the major result in the current work entails a constructive methodology,which,given a dynamical system with time discontinuities represented by rational numbers(or,equivalently,time discontinuities with a given minimal gap),yields a Caratheodory solution,which is also unique.

The classical theorem on the existence of solutions in the extended sense is due to Caratheodory[5]-[7].Recent studies in this field include topics such as well-posedness of Caratheodory solutions for bimodal piecewise affine systems[8],existence and uniqueness results for monotone nonincreasing right-hand sides[9],and extended Caratheodory solutions for hybrid systems[10].Further,when the righthand side of the system dynamics is discontinuous in the state variable,the situation becomes more complicated,than only with time discontinuities,and such notions as Filippov solutions may come into place[11],[12].The foundation of such solutions extensively utilizes the theory of differential inclusions which are also used in partial differential equations[13].Particular applications range from discontinuous stabilization[14],sliding-mode control[15],[16]and optimal control[17].An overview of Filippov and other generalized solutions may be found in[18].The proofs of these classical results rely on compactness arguments,such as Arzela-Ascoli theorem[19],and certain fixed-point theorems,such as Schauder fixed-point theorem[20]and Kakutani fixed-point theorem[21],which are,unfortunately,not constructive and do not,generally,provide explicit computational procedures[22].The current work suggests to address the existence and uniqueness of the trajectories of discontinuous systems in a constructive framework.Currently,only the case of time discontinuities is covered.However,the result can be extended onto the case of discontinuous feedback control provided that the controller implementation is considered in the sample-andhold manner(see details in Section IV).

The main contribution of this work is thus a constructive theorem on existence and uniqueness of system trajectories in the extended sense.Schwichtenberg[23],and Ye[24]addressed the case of initial value problems where the righthand side of the differential equation satisfies the Lipschitz condition(the corresponding classical theorem is originally due to Picard and Lindelof,and the corresponding description may be found in[5]).The new theorem derived in this work is a constructive counterpart of the Caratheodory’s existence and uniqueness theorem.Constructive analysis[25],which is done in intuitionistic logic[26],offers a suitable framework for the purposes of the current work.A related example application of constructive analysis to control theory was recently provided for the Lyapunov stability theory[27].

The remainder of the work is structured as follows:Section II is concerned with the key aspects of constructive analysis needed for the constructive proof of the theorem which is given in Section III.

II.PRELIMINARIES

In this section,some key notions and theorems of constructive analysis,needed for the current work,are discussed.This section mostly follows[24]since it addresses differential equations and measure theory together which will be required in the next section.First,a function f:R→R is a pair consisting of a map computing rational approximations to f(x)for any x,and a map ω :Q＞0×Q×Q＞0→ Q,called modulus of continuity satisfying the formula:

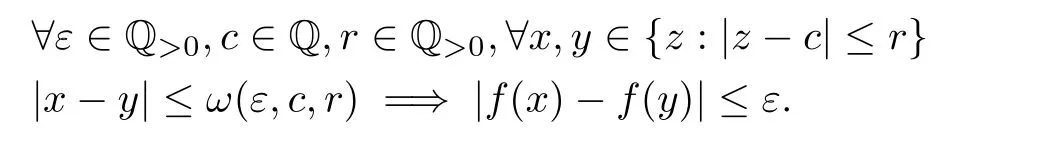
A modulus of continuity is an important certificate that every function in constructive analysis must have inside its definition.It allows computing bounds on the change of the argument that leads to a change of the function values within a prescribed bound.A function that possesses a modulus of continuity is clearly uniformly continuous.In case of∀x,y.|f(x)-f(y)|≤ L|x-y|,the function is called Lipschitz continuous.Clearly,Lipschitz continuous functions are also uniformly continuous.By default,constructive analysis is only concerned with continuous functions which are provided with continuity moduli and there is no way to define a discontinuous function directly.However,an analog of classical discontinuous functions can be defined within constructive measure theory.Further details will be given in this section.But first,the derivative and Riemann integral are defined as in the classical case[24,Chapter 3].Basic results from classical calculus are available constructively with minor modifications.In particular,Schwichtenberg[23]and Ye[24]proved Picard-Lindelf Theorem on existence and uniqueness of solutions to initial value problems,where the right-hand side is continuous,constructively.Now,integrable and measurable functions are considered.They are required to address the Caratheodory theorem which is classically stated as follows[5]-[7]:

Theorem 1:Let f(x,t)be a function on the rectangle D:[x0-b,x0+b]×[t0,t0+a];continuous in x and measurable in t.Suppose that there exists an integrable function F:[t0,a]→ R such that∀(x,t)∈ D|f(x,t)|≤ F(t).Then,there exists an absolutely continuous function ϕ on the interval I=[t0,t0+α]such that ϕ(t0)=x0and=f(ϕ(t),t)for almost all t∈I.That is,ϕ is a solution to the initial value problem x(t0)=x0,=f(t,x(t))in the extended sense.

Here,absolutely continuous means that for any ε＞0,there exists δ＞ 0 such that for any finite sequence of disjoint intervals{[tk,τk]}kon I with a total length not greater than δ,the function values at the endpoints satisfy

Now,constructive integrable functions are introduced.An integrable function is a pair({fn}n,f)such that each fn:R→R has a compact support,{fn}nhas the property that

and

on the set

called domain of f.It is said thatconverges pointwise to f on dom(f).The sequence{fn}nis called a representation of f and is invoked whenever required,but usually omitted.The Lebesgue integral is in turn defined as

Basic properties of the Lebesgue integral can be proven constructively.Integrable functions allow introducing characteristic functions of finite intervals.For example,the characteristic function χ[0,1]of the unit interval is constructed via g0(t)≡0,g1(t)≡0 and,for n＞1,

by the representation fn:=gn+1-gn.Due to undecidability of equality on R,the set A:=(-∞,0]∪(0,1)∪[1,∞)does not coincide with R constructively.This reflects the classical idea that the Lebesgue integral is not concerned with the values of a function on sets of measure zero.It can be shown that{fn}nconverges to χ[0,1]pointwise on A.

Further,measurable functions are introduced(for details,please refer to[28,Chapter.6]or[24,Chapter.6]).First,a measure of a finite interval I=[a,b]is defined asµ(I)=|a-b|.A generalized interval J is a formal union of a sequence of finite intervals{∪nIn}n,possibly overlapping.Its measure is defined asµ(J)=Pnµ(In)whenever it converges.In this case,J is called finite.A function f:R→R is called measurable if for any ε＞ 0 and any finite interval I,there exists a generalized interval J withµ(J)≤ ε and a continuous function g with a compact support such that|f-g|≤ ε on IJ.Clearly,all functions of the type

where each fjis continuous and ∀jτj＞ tj,are measurable.Integrable functions are also measurable.

Now,consider convergence of measurable functions.The key type of convergence used in the next section is convergence almost uniformly:a sequence{fn}nof measurable functions converges to a measurable function f almost uniformly if for any finite interval I and ε＞0,there exists a generalized interval J withµ(J)≤ ε such that{fn}nconverges to f uniformly on IJ.Here,the ordinary uniform convergence implies that for any ε ＞ 0,there exists N such that∀t∀n ≥ N|fn(t)-f|≤ ε on the respective set.Further,a sequence{fn}nof measurable functions is called Cauchy almost everywhere if for any finite interval I and ε＞ 0,there exists N and a generalized interval J withµ(J)≤ ε such that∀m,n ≥ N|fn(t)-fm(t)|≤ ε on IJ.An important result of constructive measure theory states that an almost everywhere Cauchy sequence converges to a measurable function:

Lemma 1:[24,pp.165]For any almost uniformly Cauchy sequence of measurable functions{fn}nthere exists a measurable function f such that{fn}nconverges to f almost uniformly,and also pointwise on the respective domain.

In the next section,a constructive variant of Theorem 1 is addressed.

III.RESULTS AND DISCUSSION

The goal of this section is to obtain a constructive counterpart of Theorem 1 which addresses numerical uncertainty.The following theorem is suggested as a particular substitute and uses assumptions which can be justified from the practical standpoint.That is,the theorem requires that the right-hand side of the differential equation have a finite number of separable discontinuities.It is easy to show that in case of indistinguishable discontinuities,the proof would imply decidability of equality over real numbers which is not true constructively.The details are given below.

Theorem 2:Consider the initial value problem

on the rectangle D=[x0- x,x0+ x]×[0,T].Suppose that

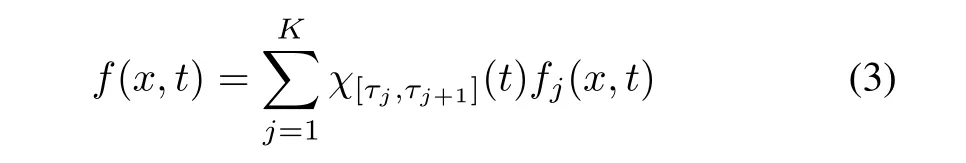
such that∀j.τj∈ Q and∃L ＞ 0∀(x1,t),(x2,t)∈ D|fj(x1,t)-fj(x2,t)|≤L|x1-x2|.Further,assume∃F＞0|f(x,t)|≤F on dom(f)=[x0-,x0+]×([0,T]{τj}j).Then,there exists a unique solution in the extended sense on a subinterval of[0,T]which depends on the initial condition uniformly continuously.

Proof:Denote domt(f):=[0,T]{τj}j.The condition τj∈ Q is needed precisely to isolate discontinuities.LetAssume that ωfis a common modulus of continuity for fj,j∈{1,...,K}on D.Consider partitions PNof[0,α]into N subintervals of length less than δ=α such that

1)ti:=α,i=0,...,N;

2)∀i=1,...,N,∀j=1,...,K+1,ti/= τj;

3)each subinterval may contain at most one τj,j=1,...,K+1.

Condition 3 is not inevitable;it is only used to simplify the proof as will be shown below.Fix some arbitrary n∈N.The number N is chosen so that the conditions 1 and 2 are satisfied and

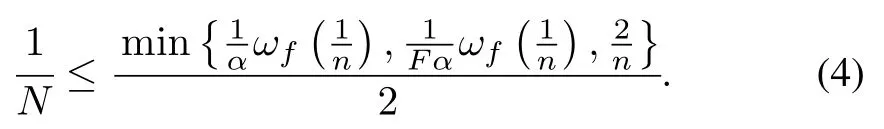
Inequality(4)is used in(5)to guarantee that(6),characterizing the precision of the solution,holds.That is,the constructed solution will satisfy the differential equation up to the precision ofNow,construct a function ϕnon[0,α]∩ domt(f)as follows:

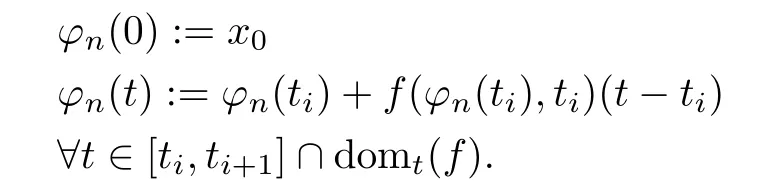
It follows that

whence(t,ϕn(t))is admissible,i.e.,(t,ϕn(t))is within D.Now,let INbe the generalized intervalsuch that each[tσ(i),tσ(i)+1]contains exactly one τj,j=1,...,K+1.Let IN:=[0,α]JN.It follows that the one-sided derivatives satisfy

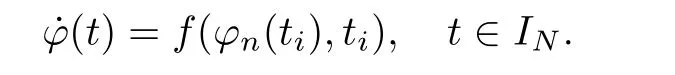
Notice that JNsatisfies

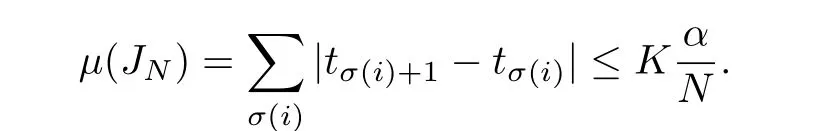
Further,for each t∈[ti,ti+1]⊂ IN,it follows that

from which it follows that

But

Furthermore,for each t∈[ti,ti+1]⊂ JN,the condition

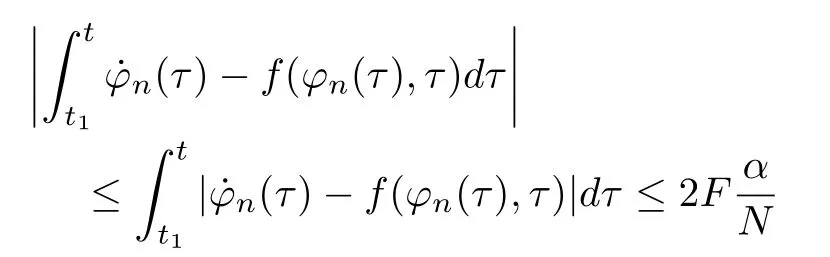
holds since f is integrable on JN.Therefore,for any t∈IN,

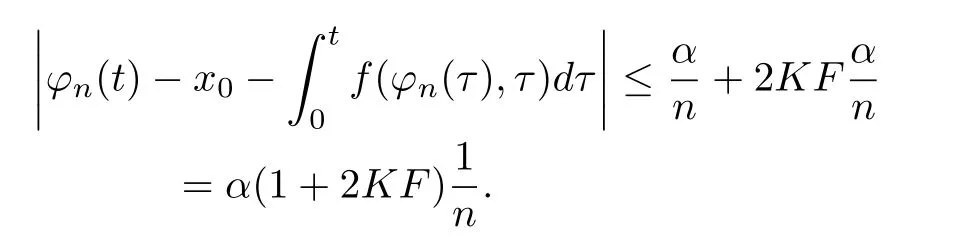
Let ϕmand the associated intervals IM,JMbe another approximate solution.Supposeand JM⊆JNwhich can be satisfied by an appropriate choice of partition points.Therefore,for t∈IN,

Let

and

It follows that:

Therefore,

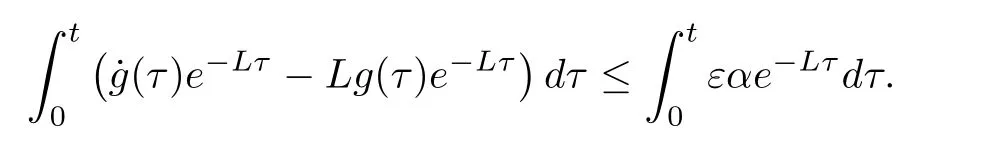
Further,

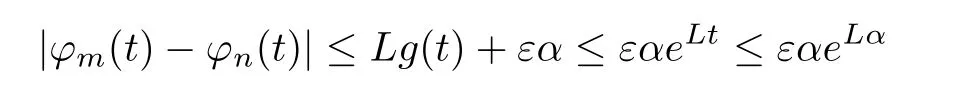
since,as from the integral above

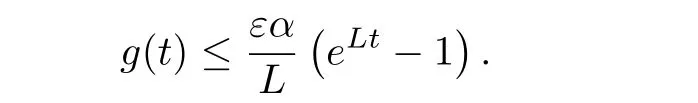
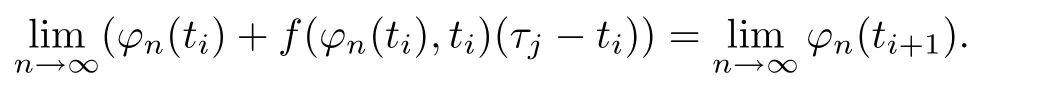
Since ti→ τj,ti+1→ τjand f(ϕ(ti),ti)(τj-ti)→ 0,it follows that ϕ can be defined on the whole[0,α][28,Lemma 3.7].By construction,ϕ is absolutely continuous.Further,˙ϕ(t)exists on[0,α]{τ1,...,τK+1}and is equal to f(ϕ(t),t).Finally,the solution is unique since

At this point,the condition holds that for any ε＞ 0,there is p∈N and a corresponding generalized interval JN(p)withµ(JN(p))≤ε such that∀m,n≥p|ϕm- ϕn|≤ ε on[0,α]JN(p)by an appropriate choice of N(p).It follows that{ϕn}nis Cauchy almost everywhere.Therefore,by Lemma 1,there exists a measurable function ϕ which is the limit of{ϕn}n.It is obvious that as n → ∞,[0,α]JN(n)→ [0,α]which means that ϕ is defined on[0,α]almost everywhere.Moreover,for any subinterval[tσ(i),tσ(i)+1],containing some τj,it follows that

where ψ(t)is a candidate solution,i.e.,

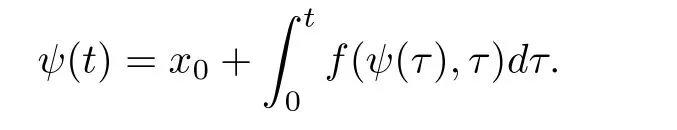
Therefore

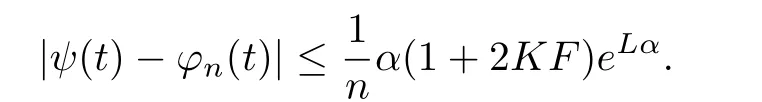
That means that{ϕn}nconverges to ψ almost uniformly.It also follows that{ϕn}nconverges to ψ pointwise on[0,α]{τ1,...,τK+1}.

Remark 1:It follows that the Picard-iteration

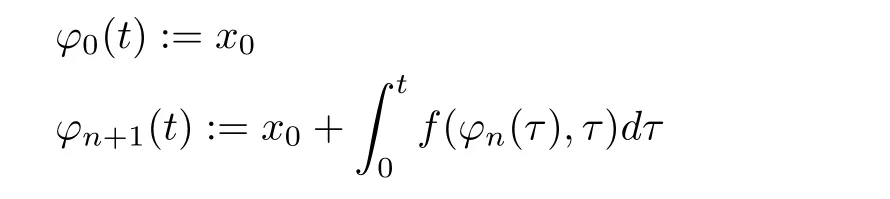
is constructively well-behaved for the presented special case of f.The generalization for systems of differential equations can be done similarly to[24,pp.107].

Remark 2:Uniform continuity of the solutions depending on the initial condition can be shown as in the standard case[24,pp.106].

Remark 3:The assumption that the time discontinuities be rational numbers can be relaxed if there is a minimal gap between them which is known beforehand.

Remark 4:Theorem 2,unlike Theorem 1,requires the time discontinuities τjto be either rational numbers or to have a distinguished gap,known beforehand.For each predefined natural number n,the proof determines another natural number N according to(4),and constructs a function which satisfies the differential equation up to the precision 1/n as stated in equation(6).The key difference of the statements thus lies in the special representation of the right-hand side(see equation 3),instead of simply requiring that f be measurable in t.This is an important aspect that allows the constructive theory of integrable and measurable functions,briefly discussed in Section II,to be used to yield a unique solution.

One may see how a failure to meet the assumption in the last remark leads to malfunctioning of the algorithm in Theorem 2.Consider,for example,sliding-mode control where an ideal trajectory is supposed to come onto a sliding surface,but,in implementation,a phenomenon called “chattering”occurs when the numerically computed trajectory jumps back and forth around the sliding surface.This chattering may well depend on the chosen sample time.It can be seen how such a case would become problematic in the method of proof in Theorem 2.Classically,one considers other types of solutions such as,for example,in the sense of Filippov[29].Constructive treatment of such cases might be a challenging task.However,there exist notions of trajectories of differential equations with discontinuous right-hand side which are based on the Caratheodory’s solutions,such as sample-and-hold[18].Theorem 2 is considered as a particular constructive counterpart of Caratheodory’s Theorem 1.It covers a large class of functions in the right-hand side of initial value problems which have a finite number of separable discontinuities.It can be seen that the method used in the proof is not constructively applicable to the case if discontinuities are arbitrary real numbers since it would lead to decidability of equality over reals.However,it is suggested that all practical problems satisfy the conditions stated.The result can also be generalized to the case where f has locally finite number of separable discontinuities.

IV.EXAMPLES

In this section,some types of dynamical systems for which Theorem 2 applies are discussed.First,the simplest case is the one in which the right-hand side of(2)possesses only one discontinuity in time.For example,consider the problem of optimal consumption in simple economy.The economy can be given by the following dynamics:

where x(t)describes the output of the economy and u(t)is the fraction of output reinvested at time t respectively.The goal is to maximize the total consumption

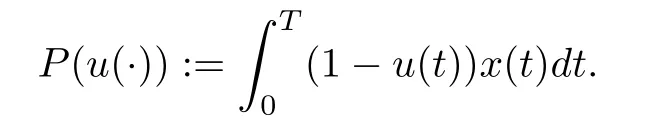
According to the Pontryagin’s Maximum Principle,the optimal control equals

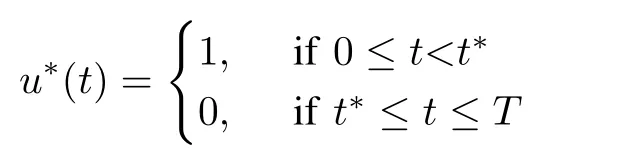
where t∗=T-1 is the optimal switching time.Since u possesses only one time discontinuity at t∗,the conditions of Theorem 2 are satisfied.The next category of control systems where Theorem 2 may be applied arises in some scheduling problems[30].For example,consider a problem of multiprocessor task scheduling in the following form:

where P(sk)is the instantaneous power consumption of executing a task at speed sk,xiis the remaining estimated minimum execution time of the corresponding task i,uijk(t)indicates that the processor j executes the task i at the speed skat time t and τijk,lijk,τijk,lijk+1is the task beginning and deadline,respectively,which must last a time amount d,minimal time slot duration,at least.Each event τijk,lijkis separated from another event τi0j0k0,li0j0k0by d as well.The scheduling dynamics are described by the state variables xiand controls uijk.It follows that for each state variable xi,the right-hand side-Pj,kskuijkhas the form(1)precisely due to the presence of the minimal time slots d.Theorem 2 addresses the case of dynamical systems whose right-hand side is discontinuous in time and continuous in the state variable.As discussed in the introduction,further generalized notions of system trajectories have to be considered in the case where the right-hand side is also discontinuous in the state variable,such as Filippov solutions.However,the problem of state discontinuities may be overcome by a special technique called“sample-and-hold”[31].This is a method of system analysis where the control variable is given by a feedback law which may itself by discontinuous in time,but is being “sampled”at certain time moments in the zero-and-hold manner.Such a setup is common in case when the controller is implemented in a digital form.This technique can be summarized as follows.Consider a partition of the interval[0,T]as a strictly increasing sequence π ={0= τ0＜ τ1＜ ···＜ τN=T}.Given a feedback law κ and a partition π of[0,T],a sampleand-hold π-trajectory of a control system˙x=f(x,κ(x,t))is defined as the solution in the extended sense of the following initial value problem:

In this case,the right-hand side takes the form:

where fi(x,t) ≡ f(x(t),κ(x(τi),τi).If f satisfies the Lipschitz condition in the sense ∀u∀x,y‖f(x,u)-f(y,u)‖ ≤L‖x-y‖ and f(x,κ(x,t))is bounded on dom(f),Theorem 2 applies if there exists a minimal gap between each subsequent τiand τi+1.Finally,Theorem 2 can be applied to some switched systems[32].Consider the following simple example:

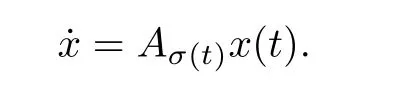
Here,a piecewise constant function σ :[0,∞) → S is the so-called switching signal where S={1,2,...,m}is a finite index set.If each Aj,j∈S is a Hurwitz matrix,the above switched system is asymptotically stable provided that there exists a sufficiently large dwell time τd＞ 0[32].The dwell time τdcharacterizes slow switching,and stability in turn can be proven by the multiple Lyapunov function criterion[32]if∀iτi+1- τi≥ τdholds.Since arbitrary fast switching is forbidden in the described scenario,Theorem 2 may be applied.

V.CONCLUSION AND OUTLOOK

This works was concerned with analysis of the Caratheodory’s theorem on existence and uniqueness of solutions to discontinuous initial value problems within constructive mathematics.A particular variant of the theorem was formulated and proven that covers a large class of practical problems.One of the future important topics is a constructive framework for other generalized solutions,such as in the Filippov sense.However,even though the case of systems discontinuous in the state variable is not addressed by the Caratheodory’s theorem,if the trajectories are to be considered in the sample-and-hold framework,the new result may be applied.In this regard,it is worthwhile to investigate constructive content of system stability under sample-and-hold control.