Modified Cuckoo Search Algorithm to Solve Economic Power Dispatch Optimization Problems

Jian Zhao,Shixin Liu,Mengchu Zhou,Fellow,IEEE,Xiwang Guo,and Liang Qi,Member,IEEE

Abstract—A modified cuckoo search(CS)algorithm is proposed to solve economic dispatch(ED)problems that have nonconvex,non-continuous or non-linear solution spaces considering valve-point effects,prohibited operating zones,transmission losses and ramp rate limits.Comparing with the traditional cuckoo search algorithm,we propose a self-adaptive step size and some neighbor-study strategies to enhance search performance.Moreover,an improved lambda iteration strategy is used to generate new solutions.To show the superiority of the proposed algorithm over several classic algorithms,four systems with different benchmarks are tested.The results show its efficiency to solve economic dispatch problems,especially for large-scale systems.

I.INTRODUCTION

E CONOMIC dispatch(ED)is one of the most fundamental optimization problems in electric power systems with the objective to minimize the total cost for power generation.It aims at economically allocating the load demand among the generators while satisfying several equality and inequality constraints in the systems.

As a classical optimization problem,ED with smooth cost functions has been solved by numerous traditional programming methods such as gradient methods[1],lambda iteration method[2],quadratic programming[3],linear programming[4],dynamic programming[5]and Lagrangian method[6].In recent years,several ED problems with some complex and non-smooth functions are proposed by considering transmission network losses and plant constraints such as valve-point effects,multiple fuel options,generation ramp rates,and prohibited operation zones.Most of the traditional techniques are not capable of efficiently solving such problems that have nonconvex,non-continuous or non-linear solution spaces.Over the past two decades,evolutionary computation developed rapidly[7]-[14].Many modern meta-heuristic algorithms and their variants were successfully used to solve such problems.According to their characteristics,they can be divided into three types:evolutionary algorithms[15]-[19],simulated ecosystem algorithms[20]-[24],and swarm intelligence algorithms[25]-[31].

Cuckoo search(CS)algorithm is a nature-inspired swarm intelligence technique based on the brood parasitism of some cuckoo species,as introduced by Yang and Deb in 2009[32].Due to its simple concept and easy implementation,CS has been successfully applied to tackle uni-modal and multi-modal numerical optimization and engineering problems[33]-[41].Many researchers have applied CS to solve ED problems in power systems[9],[42]-[48].Several studies show that CS can always find the optimal results,but it may not guarantee a fast convergence because its searching process relies entirely on a random walk[9],[36],[47].Meanwhile,a small or regular step may cause it to be trapped in a local optimal solution[48].To overcome this deficiency,a modified cuckoo search algorithm(MCSA)is proposed in this paper,where a neighbor study strategy is designed and a self-adaptive parameter selection strategy is formulated.Compared with the existing studies,we have made three contributions:

1)A new self-adaptive step size strategy is proposed such that the step decreases in different speeds as iterations proceed.In the beginning,it maintains a high value in order to enhance the exploration ability.Then,it declines rapidly to its minimum value in order to make MCSA converge steadily to a refined solution.

2)A neighbor study strategy is adopted.When the best solution is no longer updated after a number of iterations,each solution can exchange the information with others randomly.

3)A new lambda iteration method is designed to generate feasible solutions at the initial stage.In MCSA,all solutions must be feasible.A relaxation method is thus designed to handle the equality constraint that may lead to infeasible solutions.

The rest of paper is organized as follows:Section II describes the ED problem.The standard CS and MCSA are introduced in Section III.Section IV implements MCSA to solve the ED problem.Section V is dedicated to numerical simulations and results.Conclusions and future work are given in Section VI.

II.PROBLEM FORMULATION

The problem discussed in this paper is the same as those in literature[15]-[20],[26],[43].The objective of ED problem is to minimize the fuel cost of generators in electric power systems for a given load demand subject to various constraints.

A.Objective Function

The fuel function without valve-point loading of generators is given below.

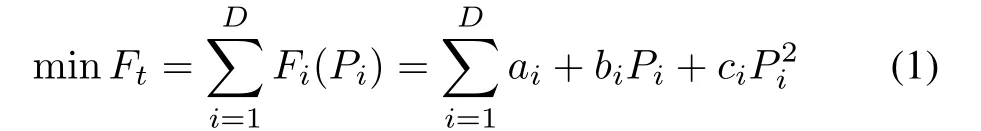
where D is the total number of generators.Fi(Pi)is the fuel cost of the i th generator with unit$/h.Piis the power in megawatt(MW)generated by the i th generator,and ai,biand ciare respectively the cost coefficients of the i th generator.

Practical large-size generators usually have multi-valve steam turbines.When each steam valve is on or off,it may produce a ripple.Usually,a sinusoidal term is added in(1)with consideration of valve-point effects(VPE)[2],thus leading to

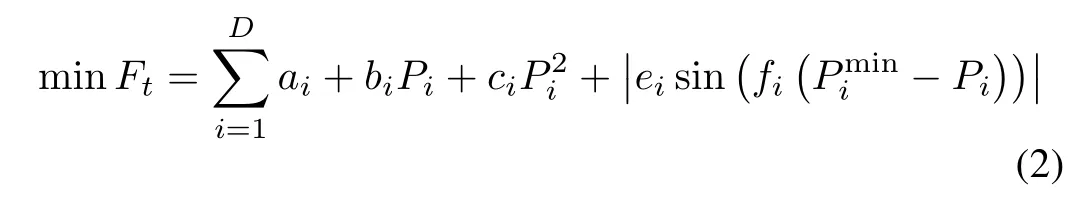
where eiand fiare constants of the valve-point effects of generators.

B.Equality Constraint

In order to balance the power,the total generated power should meet the power demand and transmission loss(TL)

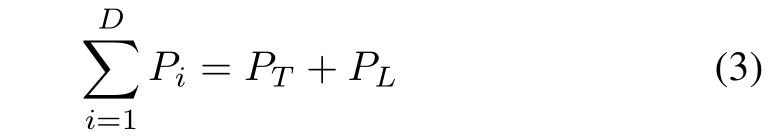
where PTis the total power demand in MW,and PLrepresents the transmission losses in MW which can be computed by using B-coefficients[2]and is given by

where Bij,B0iand B00are the loss coefficients which are constant under normal operational conditions.

C.Inequality Constraint

The output power of each generator has a lower limit and an upper one

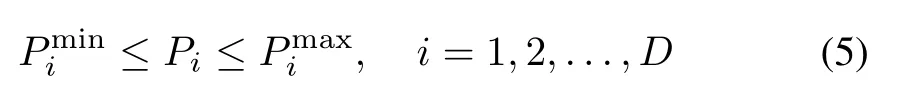
D.Prohibited Operating Zones

Each generator may have certain prohibited operating zones(POZ)caused by opening or closing its steam valve.The feasible operating zones of generator i can be described as follows:

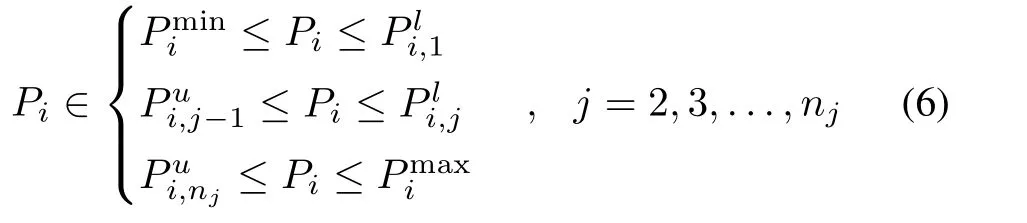
where njis the number of POZ of the i th generator,andandare the lower and upper bounds of power in the j th POZ by the i th generator,respectively.

E.Ramp Rate Limits

Practically,all generators should satisfy the physical limitation of starting up and shutting down by using ramp rate limits(RRL).The increase and reduction of power generation in each generator are limited by

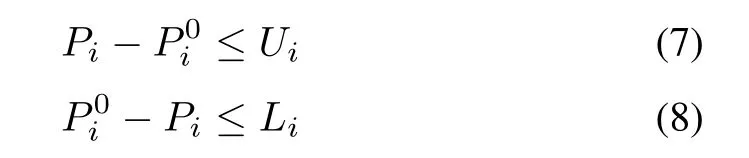
Combining(7)and(8)with(5)results in the change of the generation limits to

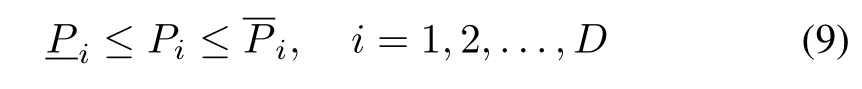
where

III.MODIFIED CUCKOO SEARCH ALGORITHM

A.Standard Cuckoo Search(CS)Algorithm

CS is a population-based swarm intelligence algorithm inspired by the interesting breeding behavior of cuckoo[32].It is enhanced by the so-called L´evy flight,rather than by simple isotropic random walks.There are mainly three rules during its searching process[49].Its main steps are given below:

1)Initialization

Suppose that there are N host nests with D dimensions.A population of these host nests could be denoted by a vector as X=[X1,X2,...,XN]TwhereEach solution is randomly generated within the boundary range of the parameters and given by

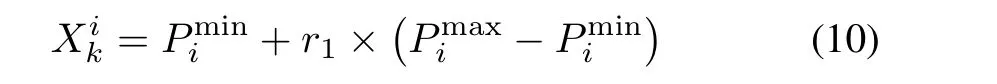
where k=1,2,...,and N represents the index of a nest in the population and i=1,2,...,and D represents the i th generator.r1is a uniformly distributed random number between 0 and 1.

2)New solution generation via L´evy flight

After initialization,CS uses a L´evy flight random walk to search a new solution,denoted by Xk(new).In order to calculate the optimal step length for the L´evy flight,one of the most effective ways is to use the Mantegna algorithm with a symmetric L´evy stable distribution[49],[50].The new solution for each nest can be formulated as follows:

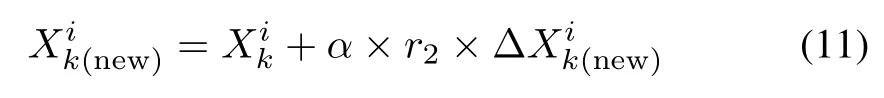
where α is the step size,and is usually set to be 0.01.r2is a random number that satisfies the standard normal distribution.is calculated as follows:

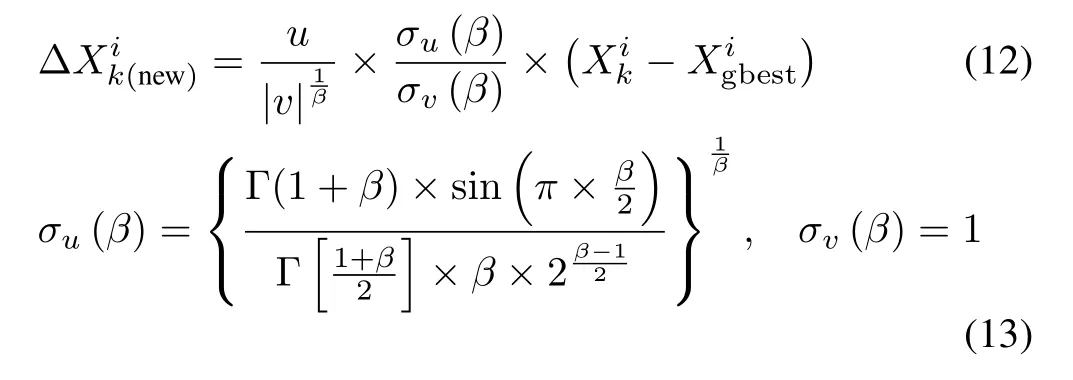
where u and v are two standard normally distributed stochastic variables with standard deviations σuand σv,respectively. β is the distribution factor satisfying 0＜β≤2 and it is set equal to 1.5 in this work,Γ is a gamma distribution function,and Xgbestis the best nest in the swarm.

3)A new solution generated via a crossover operation

The discovery of an alien egg in a nest of a host bird has a probability denoted by Pα.A new solution Xk0 is computed as

where r3and r4are random numbers that are uniformly distributed between 0 and 1.Xc1and Xc2are randomly chosen from the swarm.

The pseudo code of CS is given as Algorithm 1.

Algorithm 1 The Standard CS Algorithm

B.Self-Adaptive Step Size

α is a very important parameter for CS to find globally best solutions.CS uses a fixed value,for example α=0.01.In fact,larger α can enhance its exploration ability and avoid its falling into a local optimum in its beginning stage.As iterations proceed,smaller α makes CS converge steadily to a better solution.Inspired by[30],α is calculated as

where tMrepresents the maximum number of iterations,t means iteration t,and a and b are two positive constants satisfying a ＜ b ＜ 1.Fig.1 presents an example of α(t).Its value is ranging from 0.4 to 0.01,when a=0.39 and b=0.4.

Fig.1.Value of α(t)from 0.4 to 0.01,when a=0.39 and b=0.4.

C.Neighbor Study Strategy

In a standard CS,new solutions are generated via(14).It is obvious that solutions may easily be trapped in a local optimum if the search environment is complex with local optima.A solution may have the same values as the global optimum in some dimensions,but it has a high fitness value for a minimization problem because of the poor solutions in the other dimensions[30].In order to make a better use of the beneficial information,a neighbor study strategy is proposed to improve CS as inspired by the work[30],[31],[51].Xk0 is calculated as follows:

where K is an updated coefficient based on the probability of discovering an alien egg in its nest and is calculated as

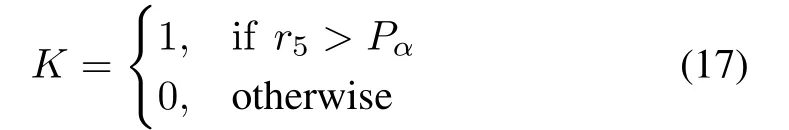
where r5is a uniformly distributed random number between 0 and 1;and Pαis the probability value of discovering an alien egg and Pα=0.25.γikis the exemplar for Xik,which is obtained from the other two solutions’competition in the i th dimension.

Every solution in the nest is able to learn from other solutions’best experiences in different dimensions.Thus,the ability of exploration is enhanced by such information sharing mechanism.Algorithm 2 describes the method of generating an exemplar Υ =[γ1,γ2,...,γN]T.In order to ensure that a solution learns from good exemplars and minimize the time wasted on poor directions,Υ is rebuilt if the best global solution is not changed in the next 3 consecutive iterations.

Algorithm 2 Generate Exemplar Dimensions for Xk

IV.MCSA TO SOLVE ED PROBLEMS

In this section,MCSA is applied to solve the ED problem.First,a new solution-generated method is introduced.Then,inequality and equality constraints’handling techniques are proposed.Finally,the main steps of MCSA are described.

A.Modified Lambda Iteration Method

In the standard CS,a solution generated via(10)is usually infeasible and difficult to repair especially in largescale systems.Thus it is necessary to propose a fast and reasonable method to solve this infeasibility problem.The classical lambda iteration was introduced in literature and applied in many software packages[2].Although it is widely used by power utilities for ED,improper selection of the initial value may cause slow convergence and sometimes leads to divergence[52]-[54].In this section we propose a method to generate a new solution effectively.Although the new solution is sometimes infeasible,it is easier to repair compared to the traditional methods especially in a system with many generators.

At the i th generator,

Then,we calculate λi,minand λi,max,i=1,2,...,D as follows:

At last,we calculate λmeanand λvarvia

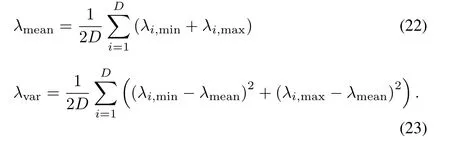
The method to generate a new solution is given in Algorithm 3.

Algorithm 3 Generate a New Solution

In Algorithm 3,sqrt represents the square root,randn represents a normally distributed pseudorandom number,and rand represents a uniformly distributed pseudorandom number.

B.Constraint Handling Mechanism

1)Inequality Constraints

The global solutions should satisfy inequality constraint(9).During the searching process,if there are some solutions that are not in the scope of the feasible solution region,MCSA may stop at the region boundary.

For constraint(6),when a unit operation is in one of its POZ,a repairing strategy is activated[43].Piviolating its prohibited zone is adjusted via

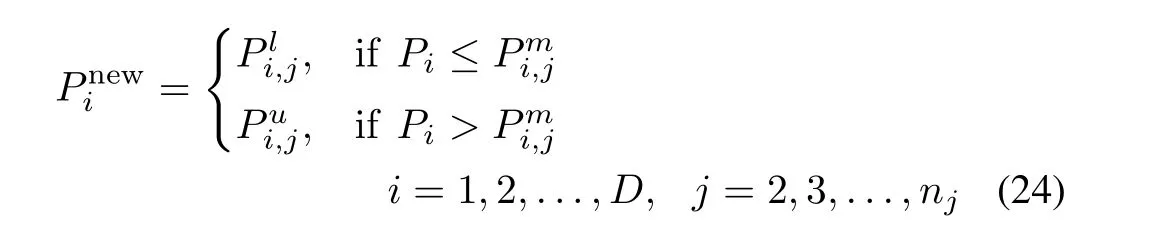
2)Equality Constraints

Although a solution satisfies all inequality constraints,it may be infeasible if it does not satisfy the power balance constraint(3).When it happens,the simplest approach for handling such infeasible solutions is to use the penalty function.However,it is well known that defining a proper penalty coefficient is difficult.Hence,a slack approach[42],[43]is used in this paper.

Assume that a slack generator s(1≤s≤D)is arbitrarily selected and the power outputs of the remaining D-1 genera-tors are known.The power output of the slack generator s is calculated as

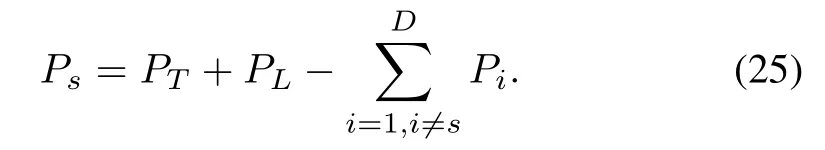
The transmission loss PLin(3)can be expressed by considering Psas an unknown variable

By substituting(26)into(25),we have

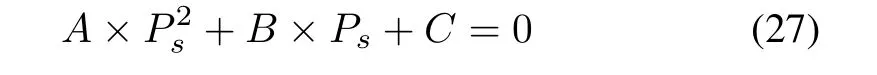
where coefficients A,B and C are given as

The power output of can be calculated by solving(27).The pseudo code is shown in Algorithm 4.

Algorithm 4 Calculate Ps Considering TL

If the return value is 0,Algorithm 4 is re-executed until solution Xkbecomes feasible.In addition,although some systems consider no transmission loss,the slack method is valid and Pscan be solved as

3)Application of MCSA for ED

In MCSA,each nest represents a solution and a population of nests are used for finding the best solution of the problem.The main steps of MCSA are illustrated in Fig.2.

Fig.2.Flow chart of MCSA.

V.CASE STUDY

In order to demonstrate the efficiency and robustness of MCSA for solving the ED problem,some cases are conducted on 6,13,20,and 40-unit systems,and the results are compared with several state-of-the-art ED algorithms in the literature.All case studies are implemented in MATLAB R2016a,on a personal computer with Intel i5 2.3 GHz processor,4 GB of RAM and Windows 10 Professional.Due to the stochastic nature of an evolutionary algorithm in each case,50 independent trials are conducted to calculate the best,mean,and worst fuel costs,and its standard deviation for each test system.

A.Parameter Selection

The performance of MCSA is sensitive to parameter settings.In this work,the parameters of MCSA described in Table I are selected based on a rigorous empirical study for each case.In this paper,the value of the self-adaptive step size α is ranging from 0.4 to 0.01 for all tested systems with b=0.4 and a=0.39 in(15).The parameters of generator count numbers(D),demanded load(PT),solution count in population(N),Pα,and maximum iteration count(tM)for all tested systems are described in Table I.In addition,the characteristics of each system such as prohibited operating zones(POZ),transmission losses(TL),valve-point effects(VPE),and ramp rate limits(RRL)are also shown in the table.

TABLE ICHARACTERISTICS FOR ALL CASES

B.System 1(Case 1:6-unit)

The first tested system is a 6-unit system which has a demand of 1263 MW with POZ,TL and RRL.Its input data are taken from[55],[56].The objective function for this system is smooth and no convexity is given by the prohibited operating zones and ramp rate limits.The best generation values,transmission losses and optimal cost obtained by MCSA are presented in Table II.Note that all system constraints,such as POZ and RRL are satisfied.The total generation cost and the corresponding transmission loss are 15 449.8995$/h and 12.9582 MW,respectively.

TABLE IIOPTIMAL GENERATIONS AND COSTS OBTAINED BY MCSA FOR CASE 1

Table III shows the obtained best cost,mean cost,worst cost,standard deviation and time for this test system after 50 trial runs.To show the differences among the results,we use four digits after the decimal point.These results are compared with other algorithms that have been reported recently such as modified artificial bee colony(MABC)[57],backtracking search algorithm(BSA)[58],differential harmony search(DHS)[59],new particle swarm optimization with local random search(NPSO-LRS)[60],particle swarm optimization(PSO)[55],multiple tabu search(MTS)[61],chaotic bat algorithm(CBA)[62],and CS[63].T O L is the difference of power balance calculated by

Through comparison,we can find that the best,mean,worst costs and standard deviation obtained by MCSA are the least.Although the best,mean and worst costs are same for MABC and MCSA,the standard deviation,time and obtained by MCSA are much better than those by MABC.The standard CS and MCSA have almost the same effect on Case 1.Moreover,it shows that the MCSA is more consistent and stable than the other algorithms.

Fig.3 shows the generation cost convergence of the best solution with iterations for CS ans MCSA for a typical run.It can be seen that both CS and MCSA enjoy smooth convergence,but MCSA is faster than CS.

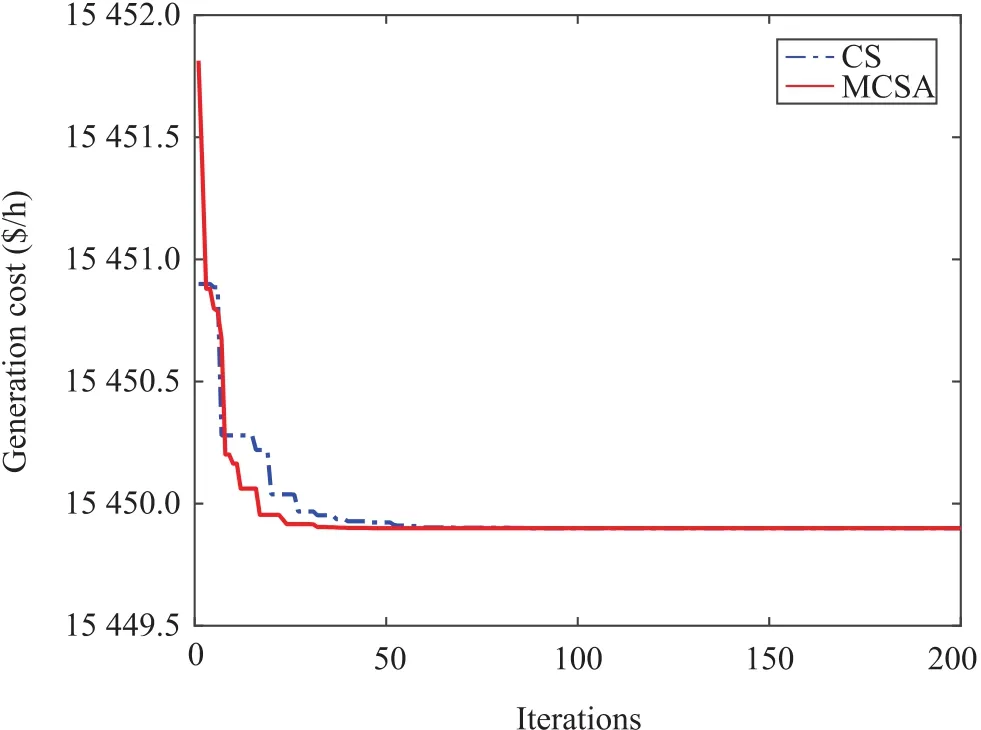
Fig.3.Convergence characteristic of MCSA for Case 1.

C.System 2(Cases 2 and 3:13-unit)

System 2 includes 13 generators and supplies a total load demand of 2520 MW with valve-point effects but without ramp rate limits and prohibited operating zones.Moreover,this system is analyzed for both“without transmission losses(Case 2)”and “with transmission losses(Case 3)”.The generator data of this system are taken from[64],and the loss coefficient is from[65]with correction Bi0[11]=-0.0017.This is a slightly larger system with more nonlinearities and local minima[66].The best generation values and the costs of Cases 2 and 3 obtained by MCSA are presented in Table IV.Note that the generation values satisfy the generation limit constraints.The total generation costs of Cases 2 and 3 are 24 169.9177$/h and 24 514.8756$/h,respectively.The transmission loss of Case 3 is 40.4266 MW.

It can be seen from Table V that the statistical results obtained by MCSA are highly competitive compared to these by MABC[57],shuffled differential evolution(SDE)[65],one rank cuckoo search algorithm(ORCSA)[67],distributed sobol particle swarm optimization and tabu search algorithm(DSPSO-TSA)[68],cross entropy method and sequential quadratic programming(CE-SQP)[66],tabu search algorithm(TSA)[68],ant colony optimization(ACO)[69]and CS.MABC,SED,ORDSA and MCSA can get the best cost,but only MABC and MCSA get the optimal mean and the leastcost.Although MABC has a good performance on standard deviation value,it usually takes much more time than MCSA.

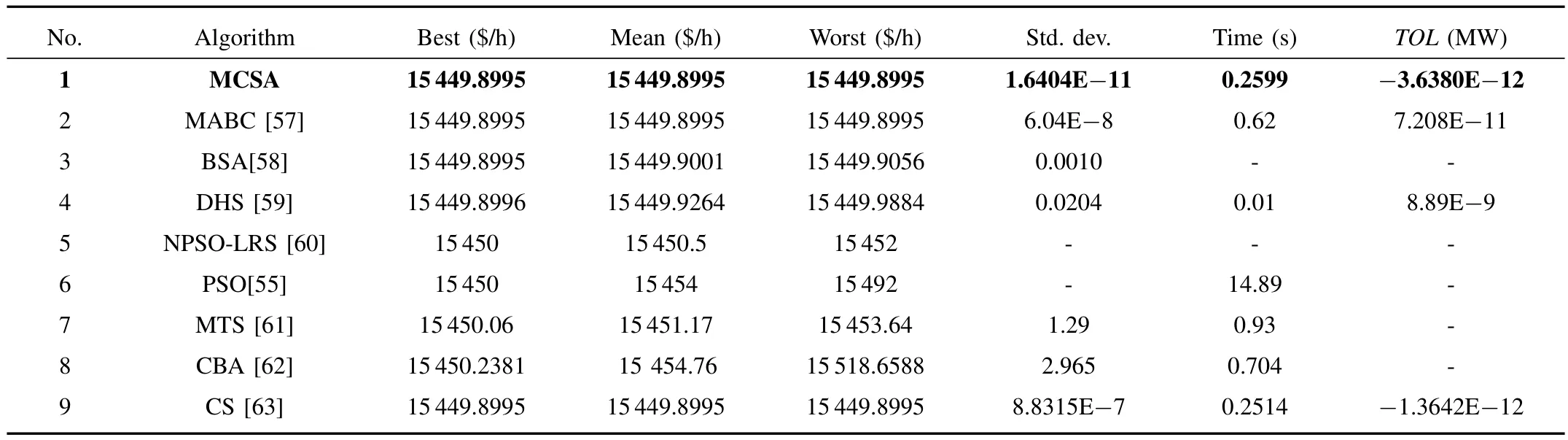
TABLE IIICOMPARISON BETWEEN MCSA AND OTHER PUBLISHED ALGORITHMS FOR CASE 1

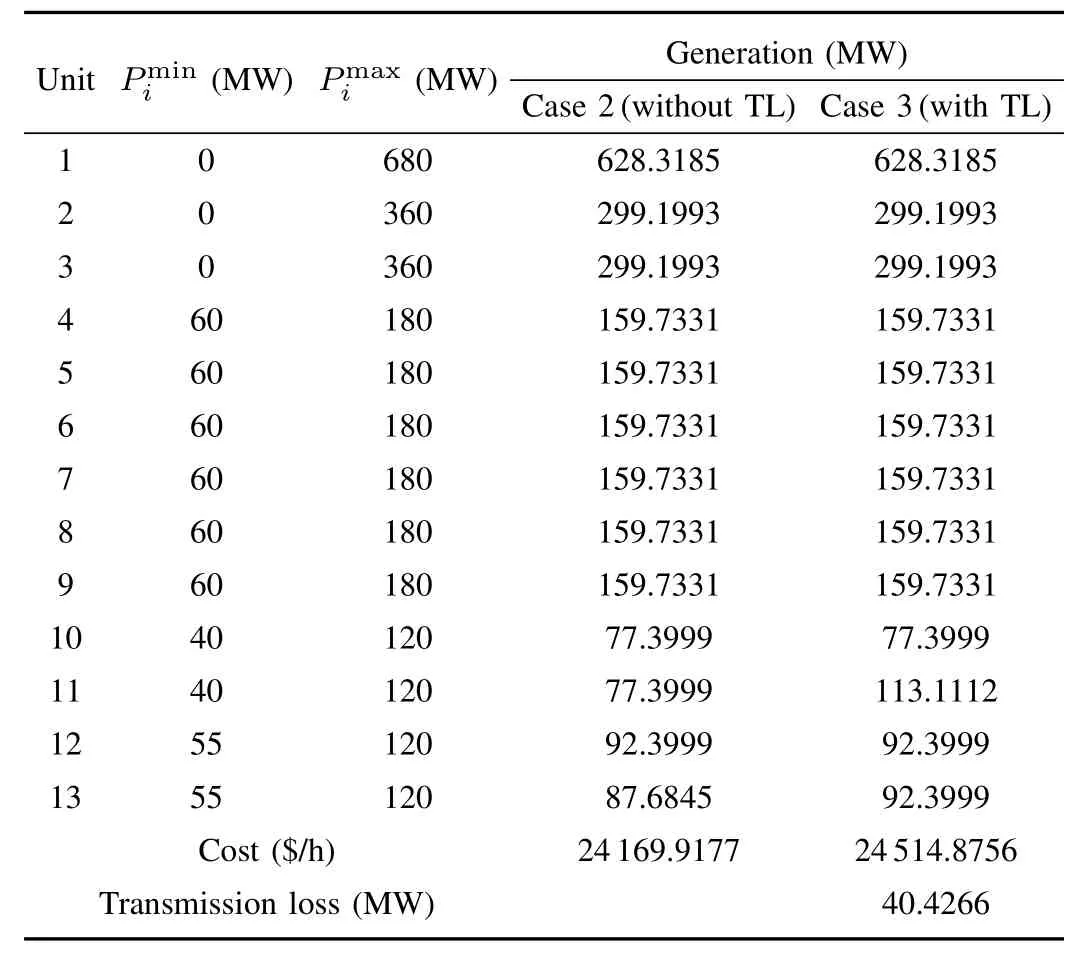
TABLE IVOPTIMAL GENERATIONS AND COST OBTAINED BY MCSA FOR CASES 2 AND 3

Table VI shows a comparison among the results obtained by MCSA and other recently published stochastic methods such as oppositional real coded chemical reaction optimization(ORCCRO)[70],MABC[57],SDE[65],biogeography based optimization(BBO)[70],differential evolution with biogeography based optimization(DE-BBO)[70],improved coordinated aggregation with particle swarm optimization(ICAPSO)[71],self-tuning hybrid differential evolution(STHDE)[16],hybrid differential evolution(HDE)[16],differential evolution(DE)[16]and CS.The best cost obtained from MCSA is the least in comparison with other methods except ORCCRO.It must be mentioned that the best cost value of ORCCRO with 24 513.91($/h)is obtained by adopting a higher tolerance(|T O LORCCRO|=0.98 MW＞|T O LMCSA|=4.5470E-11 MW)in[70].Both MABC and MCSA can find the same best,mean and worst costs in Case 3,but MCSA is superior to MABC on the standard deviation and time.

Figs.4 and 5 show the generation cost convergence of the best solution with iterations for CS and MCSA.It can be seen that both CS and MCSA enjoy smooth convergence,but MCSA converges to the optimal solution faster.

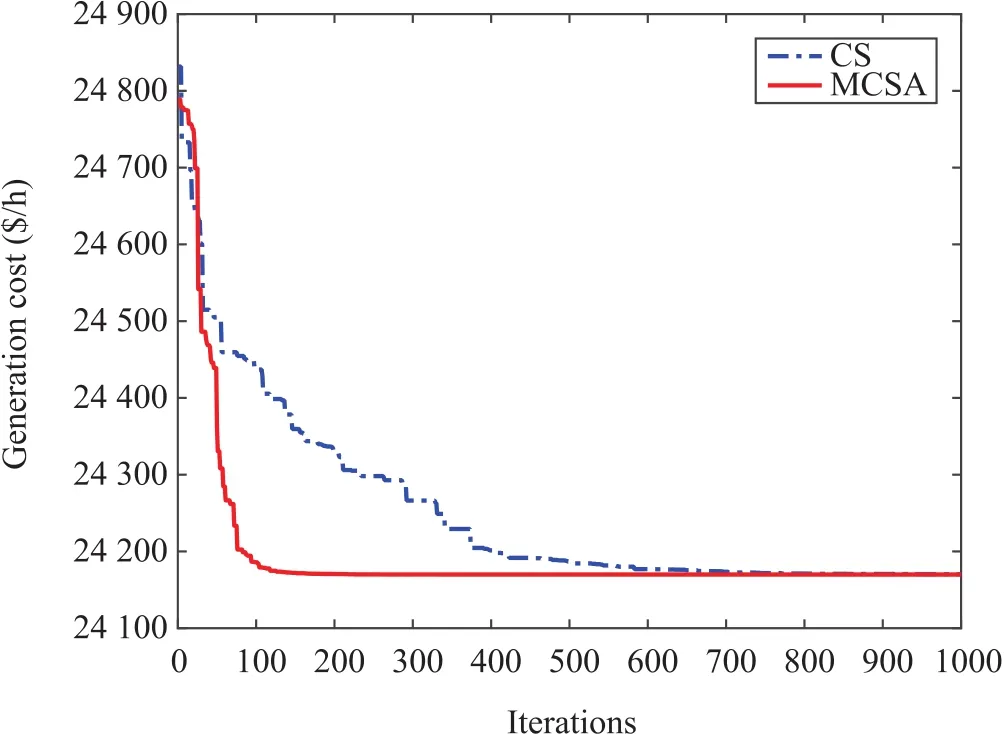
Fig.4.Convergence characteristic of the MCSA for Case 2.

Fig.5.Convergence characteristic of the MCSA for Case 3.

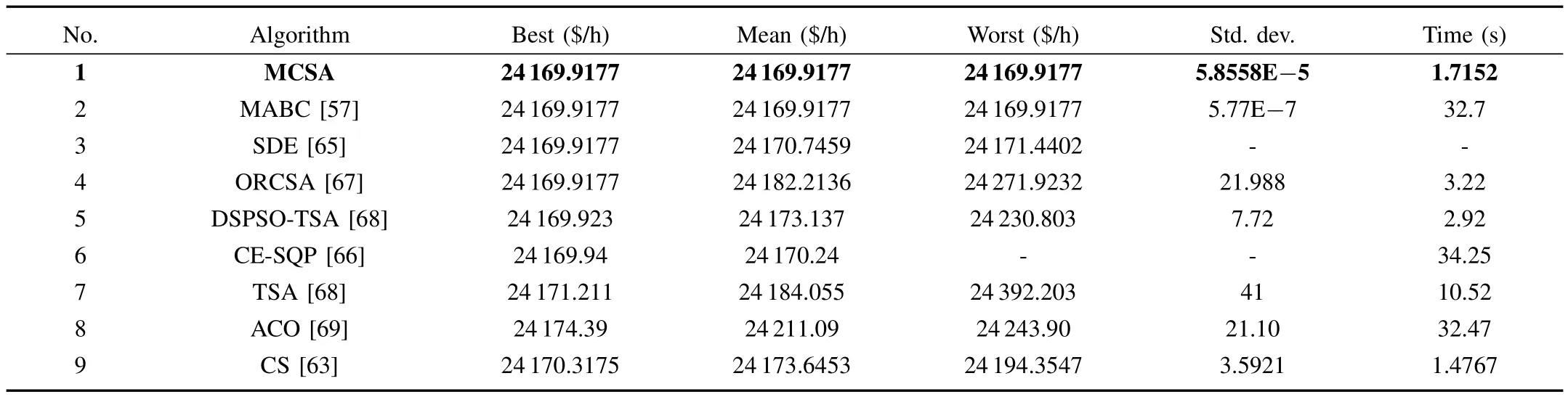
TABLE VCOMPARISON AMONG MCSA AND OTHER PUBLISHED ALGORITHMS FOR CASE 2

TABLE VICOMPARISON AMONG MCSA AND OTHER PUBLISHED ALGORITHMS FOR CASE 3

D.System 3(Case 4:20-unit)

In this subsection,the ED problem is solved for a system with 20 generators considering the transmission losses and a demand of 2500 MW.VPE,RRL and POZ are neglected.The data of this test system can be found in[72].Table VII shows the optimal generations and cost obtained by MCSA for Case 4.The optimal cost and corresponding transmission loss are 62 456.6331$/h and 91.9667 MW,respectively.

Table VIII shows the comparison among MCSA and other methods such as CBA[62],continuous quick group search optimizer(CQGSO)[73],ORCSA[67],group search optimizer(GSO)[73],backtracking search algorithm(BSA)[74],biogeography based optimization(BBO’)[75],Hop field modeling(HM)[72],λ method[72]and CS.As observed from it,the best,mean and worst cost results of MCSA are better than those of all other methods including ORCSA,GSO,BSA,BBO’,HM,and λ method and similar to those of CBA and CQGSO.The best,mean and worst costs of MCSA have the same values.Thus it verifies the robustness of the proposed method.Moreover,MCSA produces the optimal or the same standard deviation,mean and worst costs in comparison with those other than its peers.MCSA is more stable than the other optimization techniques regarding the mean cost and standard deviation.It also shows that MCSA and CS have same results for Case 4.

TABLE VIIOPTIMAL GENERATIONS AND COSTS OBTAINED BY MCSA FOR CASE 4

TABLE VIIICOMPARISON AMONG MCSA AND OTHER PUBLISHED ALGORITHMS FOR CASE 4

Fig.6 shows the generation cost convergence of the best solution among the 50 trial runs of Case 4.

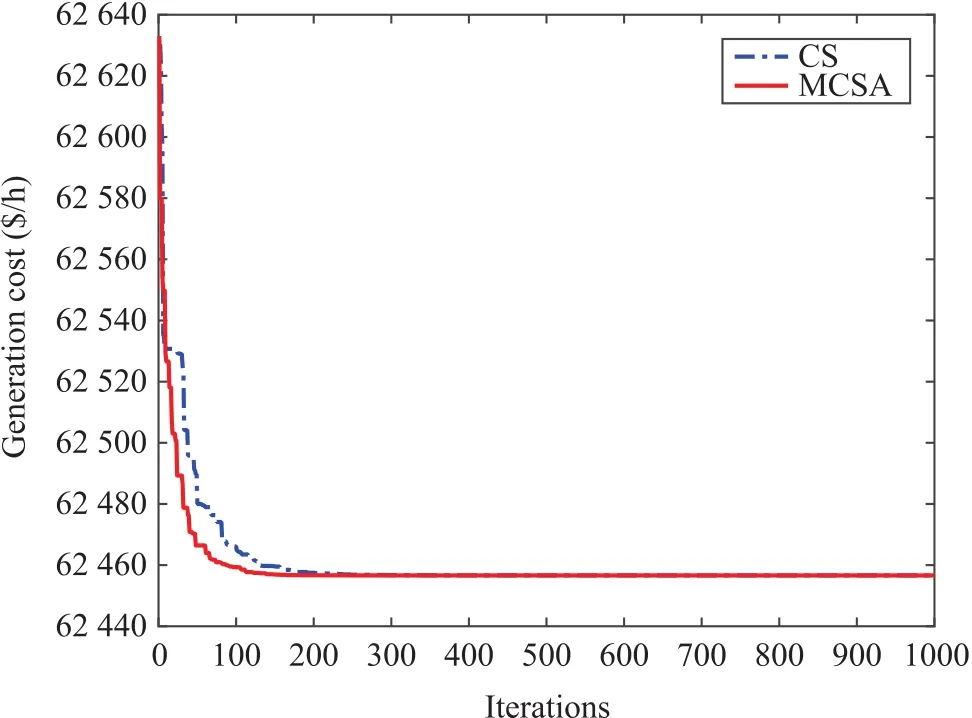
Fig.6.Convergence characteristic of the MCSA for Case 4.

E.System 4(Case 5:40-unit)

In order to further demonstrate the efficiency and scalability of MCSA,a larger system with 40 units and VPE is considered.The demand of the system is 10 500 MW neglecting TL,RRL and POZ.The fuel costs and power generation limits are taken from[64].Table IX presents the optimal generation values and cost obtained by MCSA.The optimal cost is 121 412.5355$/h.It can be seen that the generations satisfy the generation limit constraints.

Table X shows the comparison of the results obtained by MCSA and other recently reported algorithms in the literature such as exchange market algorithm(EMA)[76],ORCSA[67],CSA[43],SDE[65],MABC[57],CBA[62],new adaptive particle swarm optimization(NAPSO)[77],speciesbased quantum particle swarm optimization(SQPSO)[78],CE-SQP[66],modified differential evolution(MDE)[79],firefly algorithm(FA)[80],BSA[74],QPSO[78],BBO’[75]and CS.It shows that the best cost result of MCSA is the same or better than those obtained with other methods.Also,the mean and worst costs obtained with MCSA are better than those from its peers.Moreover,its obtained standard deviation and time are better than those from most of other methods.In summary,MCSA is more consistent and stable than the other optimization techniques.

Convergence characteristic of MCSA for Case 5 is presented in Fig.7.It shows that MCSA has better convergence characteristic in comparison with the standard CS.

Fig.7.Convergence characteristic of the MCSA for Case 5.

VI.CONCLUSION

In this paper,a modified CS algorithm is proposed.It is implemented to solve both convex and nonconvex economic dispatch problems by considering ramp rate limits,valve-point effects,transmission losses and prohibited operating zones.A slack method is used to handle equality constraints.A modified lambda iteration method is used to generate new solutions.Statistical results are compared with the reported results in literature.It is found that MCSA is capable of yielding a suitable balance between exploitation and exploration and has a better performance in terms of efficiency and robustness.All the experimental results confirm its high capability in solving ED problems.In the future,we need to develop more advanced efficient optimization methods[81]-[83]to solve power system problems involving renewable energy sources and parallel dispatch.

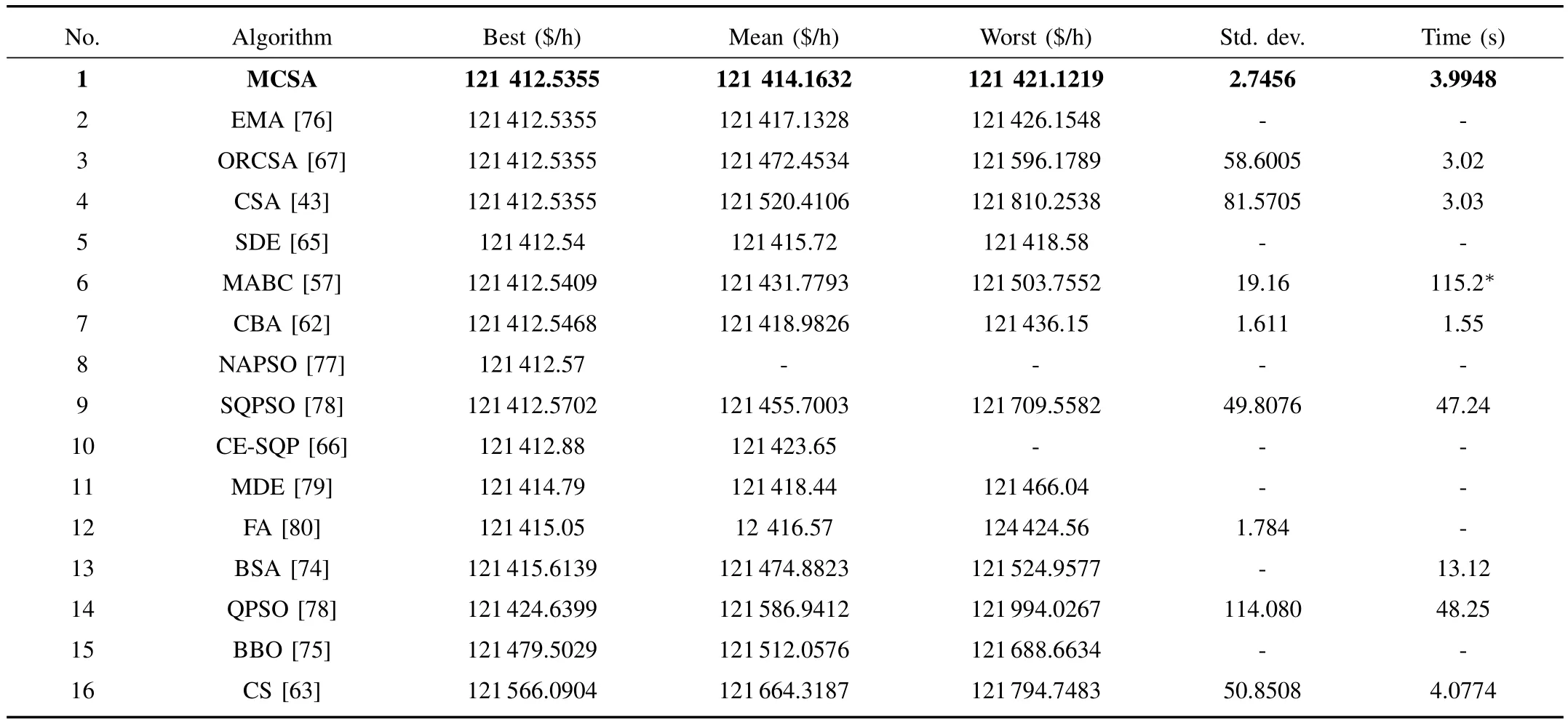
TABLE XRESULTS OF THE COMPARISON AMONG MCSA AND OTHER PUBLISHED ALGORITHMS FOR CASE 5