球头副结构尺寸对柱式力传感器方位误差影响

梁 伟

（福建省计量科学研究院 智能测量研究所，福州 350100）

随着科技和工业的飞跃发展，力传感器越来越广泛地应用于电子衡器、高速铁路、大型桥梁、高层建筑、冶金以及航空航天等领域的力值测量。应变式力传感器由球头副、弹性体、应变片及惠斯通电桥等组成，球头副由球头和球碗组成。力传感器受载时，与其接触的上下工作平面不能保证绝对平行，球头在加载过程中将相对球碗发生滚动或滑动调整，将载荷较均匀地传递给弹性体，粘贴在弹性体上的应变片受载，其电阻发生变化，使惠斯通电桥失去平衡，从而输出一个与被测载荷成线性变化的电信号。如果未采用球头副，则施加于弹性体上的载荷将出现严重偏载现象，若将传感器绕其轴线旋转到不同位置，则各位置测量得到的结果会存在较大差异，形成较大“方位误差”。因此，球头副对调整弹性体的载荷分布，提高传感器的测量准确度具有重要作用。

球头副的接触形式、尺寸、加工水平对测量结果具有显著影响，国内外专家对此开展了一些研究。[1-3]但是对于球头副如何影响力传感器计量性能，例如方位误差等，国内外未有相关报道。本课题组在研究国家重大科学仪器设备开发专项——高精度衡器载荷测量仪，以及一台目前国际上量程最大的60 MN力标准机项目中，对两个项目核心构件——高精度应变式力传感器开展研究，其中包括探索球头副对力传感器计量性能的影响。该研究成果已实现了力传感器性能的提升，并应用于此两个项目，衡器载荷测量仪于2016年实现产业化推广应用，而60 MN力标准机在2017年与德国联邦物理技术研究院（PTB）的50 MN力标准装置的力值比对取得国际等效的满意结果[4]。

本文对柱式应变式力传感器进行了理论分析，并进行实验验证，提出了优化球头副结构尺寸以减小传感器方位误差的建议。

1 理论分析

如图1所示，为一柱式传感器及其球头副结构，当其在力标准机上校准时，由于力标准机上下工作平面的不平行，假设存在倾斜角α，则球头在加载过程中相对球碗发生滚动或滑动，当球头副承载状态稳定后，球头的中心线与球碗中心线存在夹角α，如图2所示，由几何关系得：

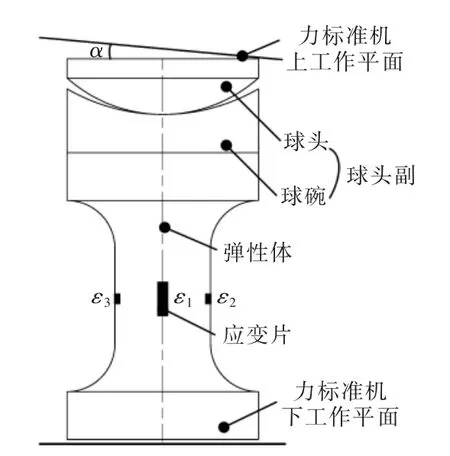
图1 力传感器及其球头副组合结构示意Fig.1 Schematic diagram of force transducer and load pad

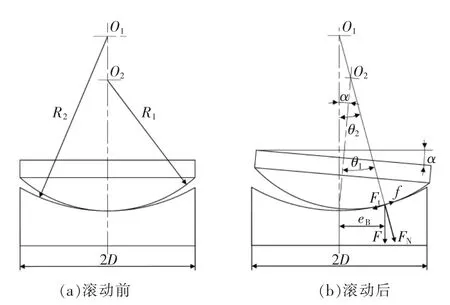
图2 球头副示意Fig.2 Schematic diagram of load pad

式中：R1为球头的曲率半径；R2为球碗的曲率半径；θ1为球头滚动前后接触点与球头圆心形成的夹角；θ2为球头滚动前后接触点与球碗圆心形成的夹角。

由式（1）得到：

球头相对球碗滚动后，传感器的轴向力为FN：

同时产生了一个侧向力Ft：

以及一个附件弯矩M：

式中：e为载荷偏心量。由图2几何位置关系可以得到：

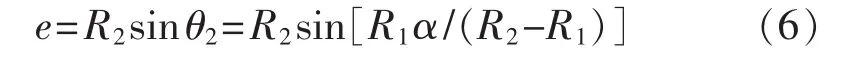
将上式代入公式，得到：

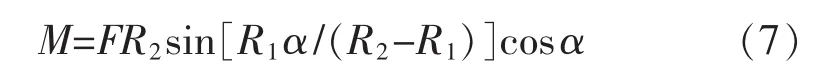
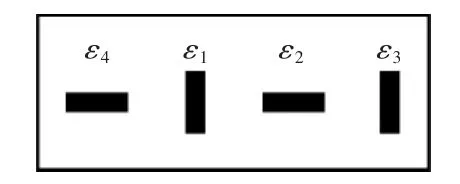
图3 应变片排布Fig.3 Strain gauges distribution

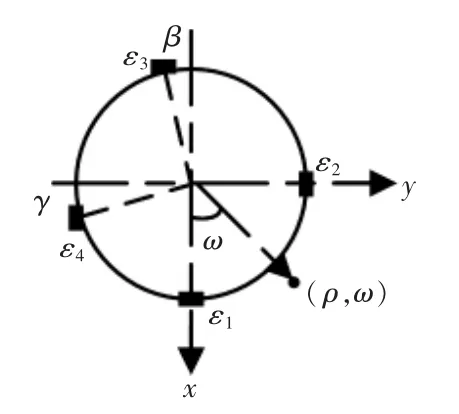
图4 应变片粘贴位置偏差示意Fig.4 Strain gauges attached with angular misalignment

如图3和图4所示，4个应变片粘贴在弹性体上，由于应变片粘贴的水平限制，4个应变片无法决定对称，而相对之间存在一定的角度偏差，如图4中β和γ。但是，传感器一旦制造完成，该角度偏差就固定下来。

依据弹性理论，在轴向力FN、侧向力Ft和附件弯矩M的共同作用下，4个应变片的输出为

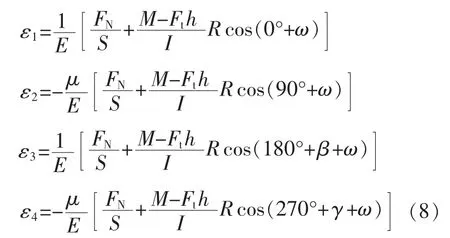
式中：S为弹性体截面的面积；ω为侧向力和附加弯矩的方位，如图4所示；R为弹性体的横截面的半径；E为弹性体材料的弹性模量；μ为弹性体材料的泊松比；I为弹性体的惯性矩，I=πR4/4。

由图5的惠斯登桥路，其输出为

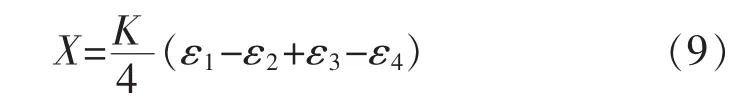
式中：X为输出信号；K为灵敏系数。

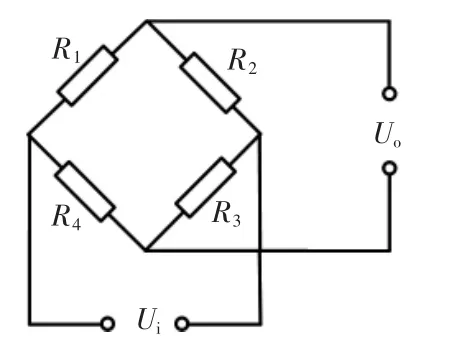
图5 惠斯登桥路Fig.5 Wheatstone bridge circuit

将式（9）代入公式，得到：

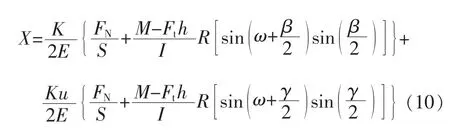
传感器的方位误差b由下式计算得到：

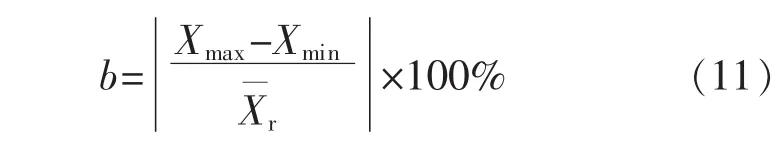
式中：Xmax和Xmin分别为传感器在不同测量位置上信号的最大值和最小值；X¯r为各方位测量的平均值。

保持传感器位置不变，将载荷绕传感器轴线转动，即可确定Xmax和Xmin，即在 ω∈［0，2π］范围内，X的最大值和最小值。将其代入式，并整理得到：

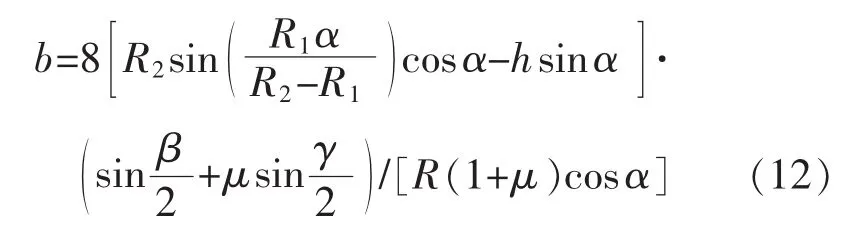
2 实验设计

为研究验证不同结构尺寸球头副对传感器方位误差的影响，本文设计了6对球头副，其具体尺寸如表1所示。所有球头副材料均为GCr15轴承钢，采用相同热处理工艺。

将6对球头副分别安装在一只300 kN和一只100 kN 柱式力传感器上， 分别在 0°、0.5°和 1°的楔形垫块上，采用一台300 kN净重式力标准机（相对扩展不确定度为0.005%，k=2）进行测试，测试步骤参照 ISO 376：2011（E）[5]进行。

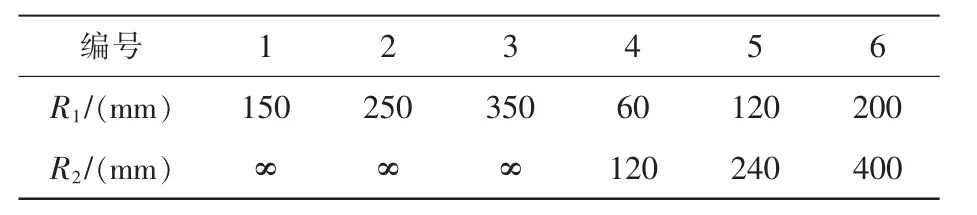
表1 球头副尺寸Tab.1 Dimensions of load pad

3 结果与讨论

图6和图7所示为各球头副分别在300 kN和100 kN应变式柱式力传感器上测量得到的方位误差，从中可以明显看出，随着倾斜角度的α增大，由式（4）和式（7），侧向力Ft和附加弯矩M也随之增大，从而造成方位误差迅速增大。

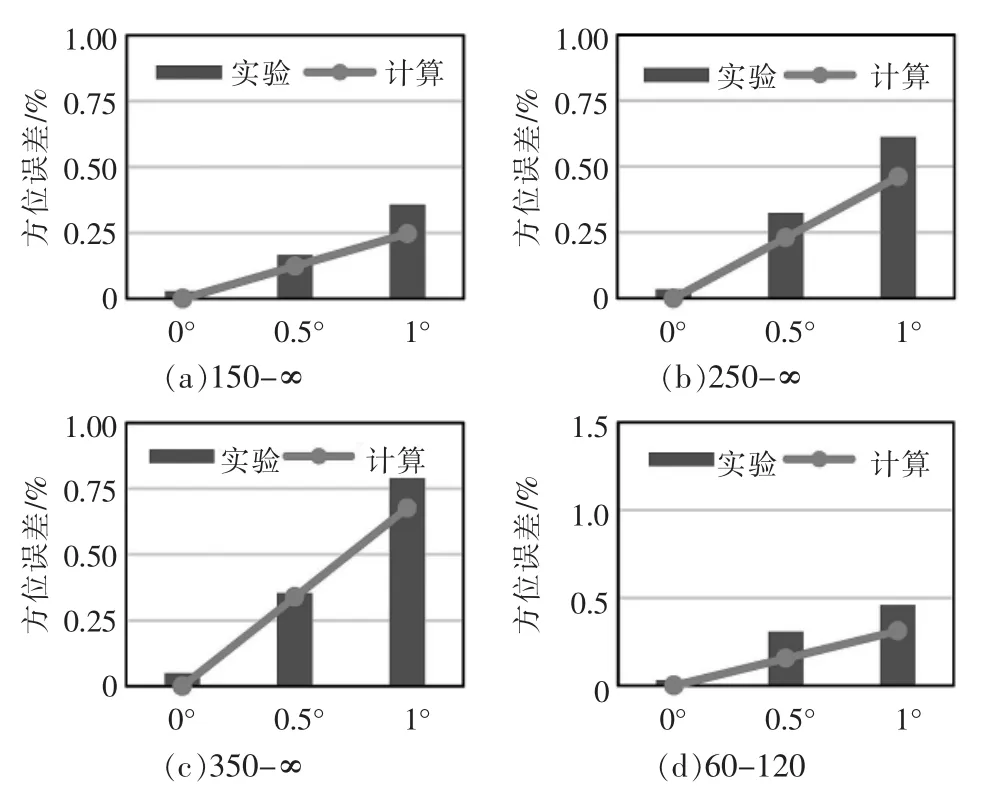
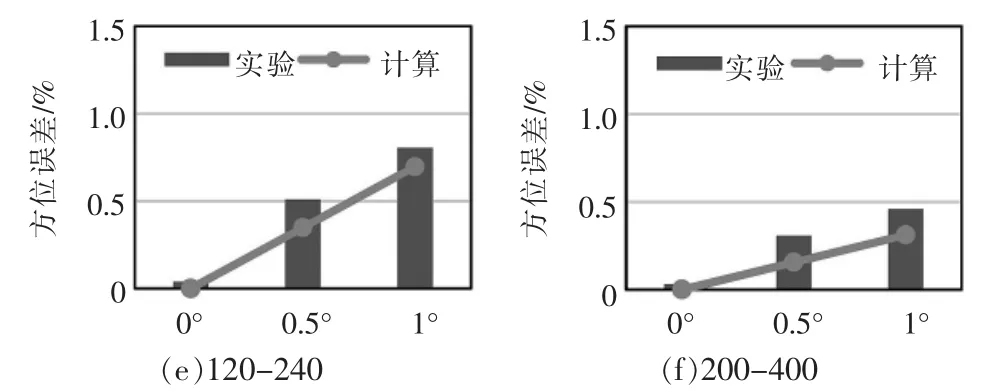
图6 300 kN力传感器采用不同结构尺寸球头实验以及计算得到的方位误差对比Fig.6 Comparison of the 300 kN transducer’s position errors between the measurement and calculation

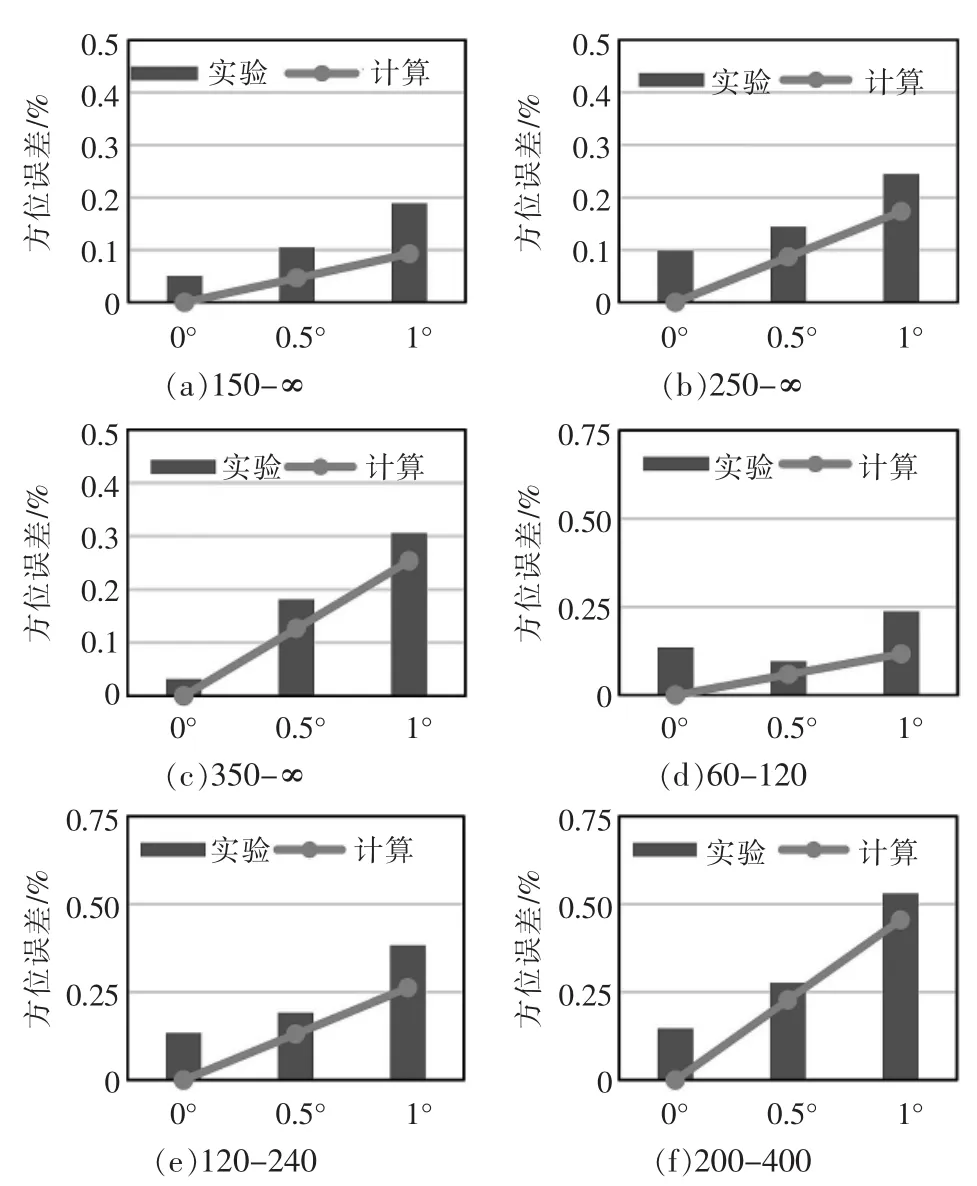
图7 100 kN力传感器采用不同结构尺寸球头实验以及计算得到的方位误差对比Fig.7 Comparison of the 100 kN transducer’s position errors between the measurement and calculation

对比1号、2号和3号球头副，其均为球面-平面接触类型，球头球面半径R1越大，方位误差随倾斜角度增长的速度越快。由式（7）可以得到，当球碗为平面时，即R2=∞ 时，M＝FR1αcosα，附加弯矩M与R1成正比，因此R1越大，附加弯矩M也越大，方位误差也越大。

对比4号、5号和6号球头副，其均为球面-球面接触类型，球头与球碗的球面半径比Δ，Δ＝R1/R2＝1/2，球头球面半径R2越大，方位误差随倾斜角度增长的速度也越快。 由式（7），M=FR2sin［Δα/（1-Δ）］cos α，当Δ相等时，附加弯矩M与R2成正比，R2越大，附加弯矩M也越大，方位误差也越大。

对比由式（12）计算得到的各球头的方位误差以及由实验测量得到的方位误差，可以看出两者相差很小，理论推导的方位误差公式可以准确地计算电阻应变式柱式力传感器的方位误差并预测其在不同球头副结构尺寸影响下的变化规律。当传感器制造完成，应变片角度偏差β和γ即固定不变，式（12）中的sin（β/2）+μsin（γ/2）一项即为常数，R2=∞ 时，方位误差随R1增大；同样，对于相同的球面半径比Δ，应该严格控制R2尺寸，从而减小传感器的方位误差。此外，由该公式可以预测，如果保持R2不变，则Δ越大，产生的附加弯矩M也越大，其得到的方位误差也越大。

4 结语

本文对柱式应变式力传感器的方位误差进行了理论分析，并通过不同结构尺寸的球头副实验验证，得到结论如下：

理论推导的方位误差计算公式可以准确地计算柱式力传感器的方位误差并预测其在不同球头副结构尺寸影响下的变化规律；柱式力传感器的方位误差与施加在其上的附加弯矩有关，弯矩越大，产生的方位误差也越大；对于球面—平面接触类型球头副，应严格控制球头半径R1尺寸，在材料强度允许的调节下，R1应尽量小；同样，对于球面—球面接触，应该尽量控制球碗半径R2和半径比Δ，从而减小传感器的方位误差。