基于改进元胞传输模型的交叉口信号配时优化
2018-07-31邹娟,刘斌
邹 娟 ,刘 斌
(1.武汉科技大学 信息科学与工程学院,武汉 430081;2.冶金自动化与检测技术教育部工程研究中心,武汉 430081)
随着人们对交通需求的不断增加,交通拥堵成为当今社会一大难题。在交通基础设施跟不上交通量增长速度的前提下,交通信号优化成为改善交通拥堵的必要手段。为描述交通流特性以及拥堵形成转化的过程,学者们提出了许多交通流模型。其中包括元胞传输模型CTM,该模型是Daganzo于1994年提出的一种宏观交通流模型,是对宏观动力学模型LWR模型的离散化近似[1]。目前已广泛应用于网络交通流模拟[2-3],交通信号灯控制[4-5],动态交通分配[6]等方面。
为了使CTM更接近于实际交通流的传播规律,文献[7]针对交叉口队列疏散的实际特性,将饱和状况下通常为常量的传统的需求函数改为线性递减函数,改进了元胞传输模型。文献[8]在CTM中采用随机分布的饱和流率和到达率,通过遗传算法来优化简单路网中的配时方案以达到减小路网车辆延误的目的。城市路段上行驶着多种类型的车辆,每种类型的车辆都有各自的交通流特性,需要不同的方法进行控制。因此要求交通流模型在保持良好的计算效率的同时,能够捕捉和描述更为复杂的交通流运行的动态特性。文献[9]考虑到不同类型车辆间长度与速度的差异,基于单类型CTM提出了多类型的元胞传输模型M-CTM,能更好地描述车流运行状况。但模型对于流量的计算较繁琐,在交叉口信号优化的应用上有时效性约束。
考虑到交叉口接近饱和状态时,不同类型车辆的速度差别较小。为提高算法效率,本文忽略速度的差异,仅考虑多种类型车辆长度的影响,提出了改进的元胞传输模型。通过分析饱和交叉口车道溢流的现象,建立了适用于多个相位控制的交叉口信号配时优化模型。由于蜜蜂算法能快速收敛于最优解且不易陷入局部最优解,因此本文采用蜜蜂算法对该模型进行动态优化以得到最优信号配时方案。
1 模型建立
1.1 改进的元胞传输模型
城市道路上车辆类型多种多样,其交通流特性也各不相同,为简化计算,假设各类型车辆的自由流速度相同,且均匀分布在元胞中,仅考虑车辆长度的影响。与CTM类似,改进的CTM同样将道路划分为多个等距离的小段,每个小路段就是一个元胞,并将时间离散化,细分为相等的时间步长。对不同类型的车辆分类,根据各自的车辆长度从大到小划分为1到M类,定义元胞长度为车辆以自由流速度在一个时间步长内行驶的距离。对于改进的CTM,定义如下模型参数和变量:
m:车辆类型索引值,m=1…,M;
Si(t):第t个时段元胞i的发送能力;
Ri(t):第t个时段元胞i的接收能力;
nm,i(t):第t个时段元胞i中m类车辆数;
lm:m类车辆相对于M类车辆的归一化长度,其值等于m类车辆与M类车辆的长度之比;
Qi(t):第t个时段元胞i的流入能力(定义为M类车辆的最大流入量);
v:自由流速度;
w:拥挤时的反向激波速度;
Ni(t):第t个时段元胞i的最大承载能力(定义为元胞能容纳的最大M类车辆数);
fi(t):第t个时段进入元胞i的总流量;
ym,i(t):第t个时段元胞i中m类车辆的流入量。
元胞的发送能力Si(t)和接收能力Ri(t)分别为第t个时段元胞i能流出的车辆数和所能接收的车辆数。在改进的CTM中,考虑车辆长度的影响,将文献[9]中的元胞发送能力与接收能力简化为
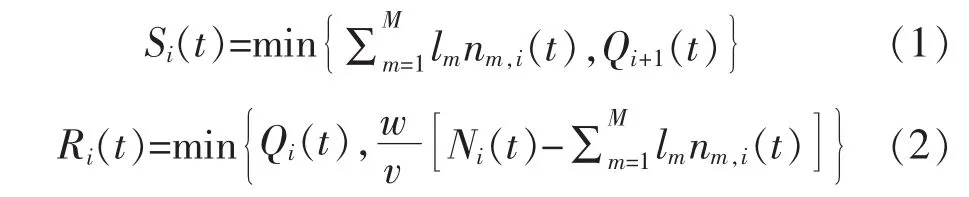
第t个时段进入元胞i的总流量为
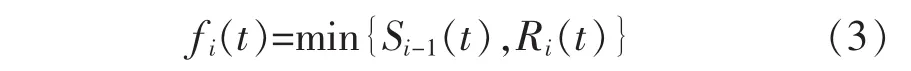
那么每种类型的车流量为
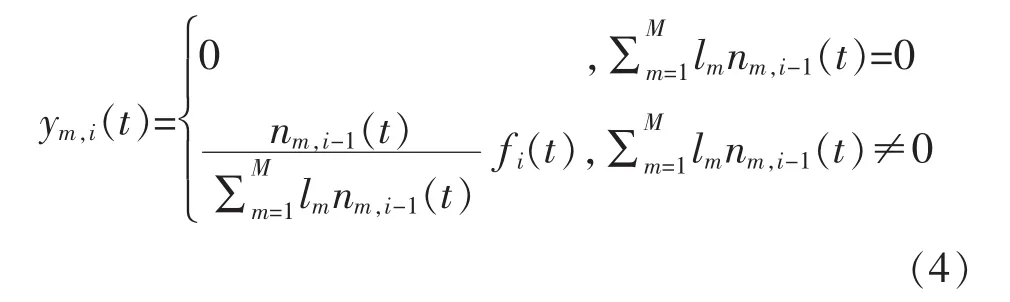
元胞上的车辆数可根据下式来更新:
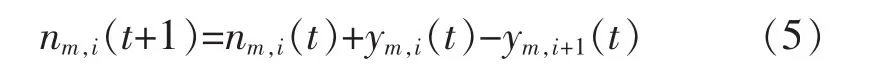
由以上式(1)~式(5)构成了本文改进的CTM的基本路段模型。
1.2 基于改进CTM的交叉口配时优化模型
一个十字交叉口由4条进口链路和4条出口链路组成,假设每个进口链路由λ个元胞组成,前λ-1个元胞为混行区,只有末尾元胞λ根据不同的车流方向被渠化为不同的子区域,形成不同方向车流的排队等候区域。通常情况下,右转车流与其它方向的车流没有冲突,因此在本文的信号配时中不予考虑。于是链路l的元胞划分如图1所示。
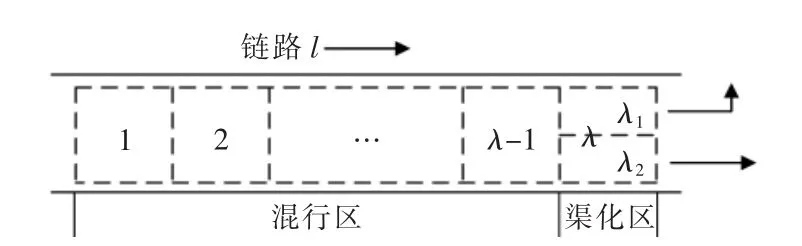
图1 交叉口元胞划分Fig.1 Cell division of intersection
1.2.1 考虑车道溢流现象的分流模型
如果某个出口发生堵塞,后面的车流若想驶入正确方向的渠化区,就会在车道上出现车道溢流的现象[10](如图2)。若不能及时进行疏散,可能会延伸甚至跨越到其他车道导致这个进口道的堵塞。
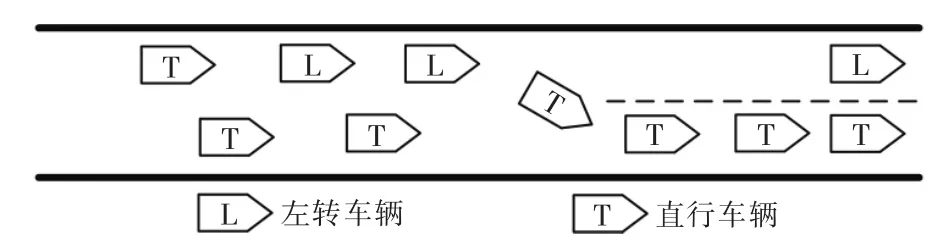
图2 车道溢流现象Fig.2 Lane overflow phenomenon
用k索引渠化元胞λ的子元胞,k=1,2,记λk为渠化区第k个子元胞,αm,k为m类车辆在渠化区的分流比例。那么对于任意m,有。 车辆在流出元胞λ-1时会根据分流比驶入相对应的车道,分流情况如图3所示。
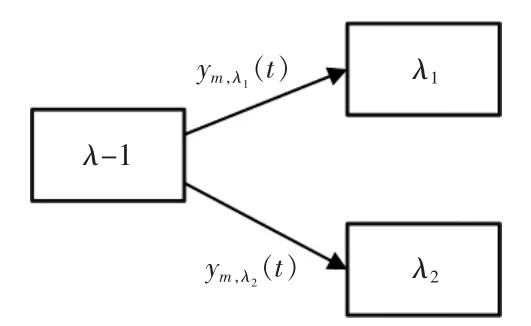
图3 渠化元胞的分流模型Fig.3 Diverging model of channelized cell
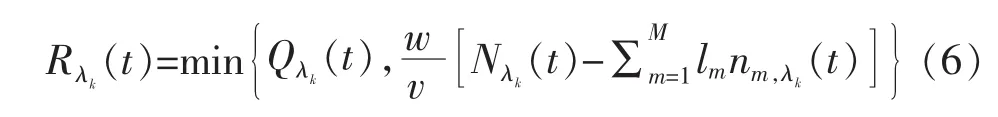
式中:子元胞 λk的流入能力Qλk(t)和最大承载能力Nλk(t)可根据渠化区各方向的车道数得到。
考虑到车道溢流的现象,在计算渠化区子元胞的流入量时需要找出最先达到极限容量的渠化子元胞λk*,即最先出现拥堵导致车道溢流现象发生的子元胞。定义:
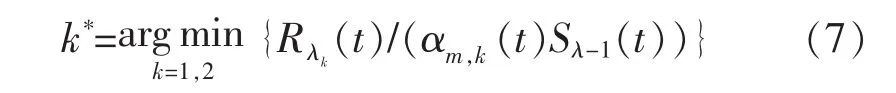
定义渠化子元胞λk的接收能力为
先计算能够流入子元胞λk*的总流量:
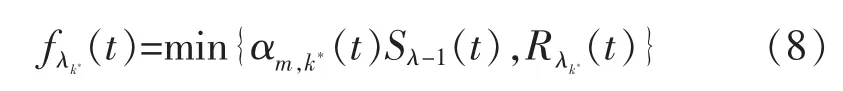
每种类型的车流量可由下式表示:
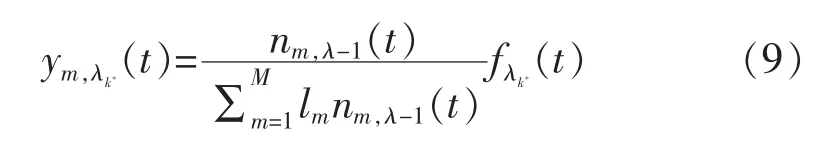
那么其他渠化子元胞的流入量可根据分流比来计算:
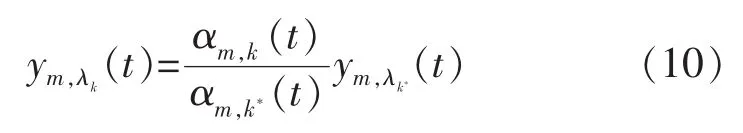
式(6)~式(10)构成了渠化元胞的分流模型。
1.2.2 信号控制
为方便描述,定义ym,λk+1(t)为渠化子元胞 λk中m类车辆的流出量,Qλk+1(t)为渠化子元胞 λk的流出能力。对于受信号灯控制的元胞λk,其流出能力Qλk+1(t)取决于当前时刻所处的相位,则:

式中:s为M类车辆的饱和流率。确定了渠化区子元胞的流出能力后,各类型车辆的流出量也就能确定下来,即:
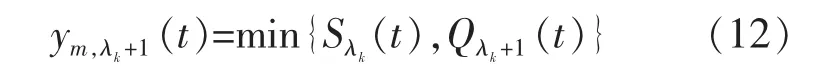
1.2.3 目标函数与约束条件
交叉口信号控制的评价指标通常有排队长度、平均停车次数、车辆延误等。在元胞层面,一个时间步长内车辆延误为除自由流走行时间外车辆通过元胞的额外时间[10],即上一时段等候在当前元胞的车辆会产生一个时间步长的延误,则元胞i中m类车辆在第t个时段的总延误为
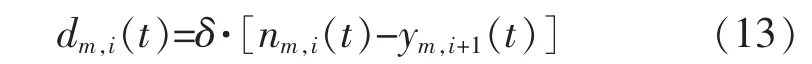
那么整个交叉口的车辆平均延误也可以确定下来,仅考虑进口链路车辆的延误,则目标函数为
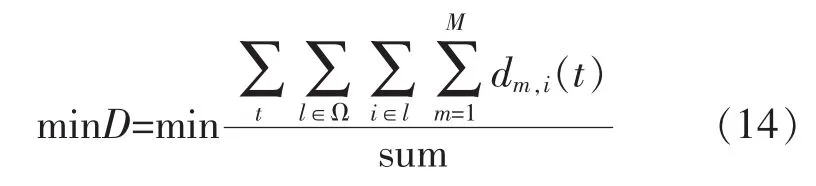
式中:Ω为进口链路集合;sum为仿真时间内进入交叉口的总车辆数。在交叉口设置传统的四相位信号,相位方案如图4所示。
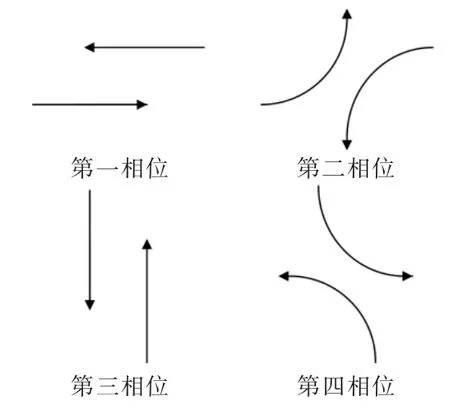
图4 交叉口相位图Fig.4 Intersection phase diagram
不考虑黄灯和全红时间,有以下约束条件:
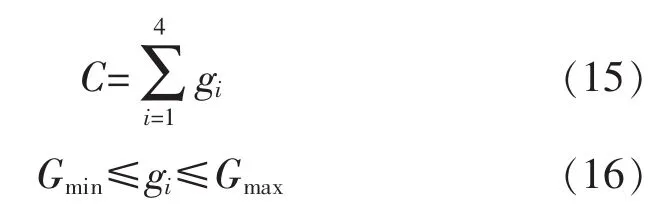
式中:C为信号周期时长;gi为第i相位的通行时间;Gmin与Gmax分别为各相位最小和最大的绿灯持续时间。
2 算法设计
2.1 蜜蜂算法
蜜蜂算法BA由英国学者D T Pham于2005年提出[11],是一种受启发于蜜蜂觅食行为来寻找最优解的智能优化算法,该算法将邻域搜索和随机搜索相融合来实现最优化。目前在国外蜜蜂算法已经广泛应用于不同的优化问题中,如机械设计,作业车间调度,供应链优化,神经网络训练,机器人路径规划以及化工问题和装配问题。算法具体步骤如下:
步骤1随机初始化ns只侦查蜂的位置,并计算各自的适应度;
步骤2根据适应度选择nb个较好的站点进行邻域搜索;
步骤3从nb个较好站点中选择ne个最优站点,每个站点招募nre只蜜蜂进行邻域搜索,计算各自适应度;
步骤4对于剩余nb-ne个较好站点,每个站点招募nrb(nrb 步骤5为每个较好站点选择适应度最好的那只蜜蜂,共得到nb只蜜蜂; 步骤6若邻域搜索无法找到更好适应度的站点,缩小邻域范围; 步骤7当连续停滞的次数超过一限定值stlim时,终止该站点的邻域搜索并随机产生新的站点代替该站点适应度最高的那只蜜蜂,并计算适应度; 步骤8分配剩下的侦查蜂进行随机搜索,并计算适应度; 步骤9形成新的种群,包括在较好站点进行邻域搜索得到的nb只蜜蜂,以及进行随机搜索的ns-nb只侦查蜂,记录本次迭代适应度最好的位置; 步骤10跳转至步骤2,直到满足迭代终止判定条件。 本文采用蜜蜂算法对上述交叉口模型进行优化,基于改进CTM的交通流模拟以及动态信号配时优化步骤如下: 步骤1初始化各元胞上的各类车辆数以及每个时间步长内进入交叉口的各类车辆数; 步骤2调用蜜蜂算法,加载当前交通流状态,应用基于改进CTM的交叉口模型进行一个信号周期内的交通流动态模拟,以一个信号周期内的车辆平均延误为优化目标,得到最优信号配时方案; 步骤3加载蜜蜂算法优化得到的最优配时方案进行一个周期的交通流动态模拟,保存当前周期最优配时方案下的交通流状态作为下一个周期信号优化的初始状态; 步骤4仿真时间到则停止模拟,否则跳转到步骤2进行下一个周期的信号配时优化。 为验证上述模型的有效性,本文选取城市道路中常见的小汽车和公交车作为交通主体,采用Matlab进行仿真分析。元胞传输模型参数设置如下:每个进口链路设置6个元胞,时间步长δ取为10s,信号周期为120s,仿真时长为600s(即5个周期),小汽车和公交车的长度分别为5m和12m,每个车道小汽车的饱和流率为2160辆/h。蜜蜂算法相关参数设置如下:迭代次数为20,较好站点为5个,最优站点为2个,随机搜索站点为5个;最优站点招募的蜜蜂数目为10,余下较好站点招募的蜜蜂数目为3,停滞次数为5。 在仿真中,分别在2种不同的初始状态下对交叉口配时方案进行动态优化。①无阻塞情况:仿真开始时交叉口无车辆;②阻塞情况:仿真开始时南进口链上某处发生阻塞,导致第五个元胞上存在5辆公交车和30辆小汽车。两种情况下均加载相同的交通需求。 在仿真时间内固定配时如表1所示。在各进口链路流量不变的情况下,采用本文提出的动态配时方法在仿真时间内得到的配时结果如表2和表3所示。两种情况下固定配时与动态配时在仿真周期内的车辆平均延误对比如表4所示。 从表4中可以看出,在仿真的5个周期内,通过动态地优化配时方案,有效地降低了交叉口的车辆平均延误。在道路没有阻塞时,虽然对于单个车辆延误的差值看起来不大,但能大幅降低整个交叉口的总延误。而在道路某处发生阻塞时,动态优化配时方案能够及时响应交通流的变化,避免固定配时下阻塞车辆无法及时进行疏散的情况,从而有效地提高交叉口的通行能力。 表1 固定配时Tab.1 Fixed timing 表2 非阻塞情况下的动态配时结果Tab.2 Dynamic timing results in unobstructed condition 表3 阻塞情况下的动态配时结果Tab.3 Dynamic timing results in obstructed condition 表4 车辆平均延误Tab.4 Vehicle average delay 本文通过分析车道溢流现象,考虑不同类型车辆间长度的差异,建立了基于改进元胞传输模型的交叉口配时优化模型,该模型能动态模拟出路段上各类车辆的流量与密度间的关系。采用蜜蜂算法作为优化工具来最小化车辆平均延误。最后通过数值仿真验证了模型的有效性,结果表明提出的模型同时适用于交叉口无阻塞和阻塞的情况,且本文提出的动态配时优化方案在阻塞情况下具有更好的效果,能有效降低交叉口车辆延误。2.2 动态信号配时优化
3 数值模拟
3.1 参数设置
3.2 仿真结果


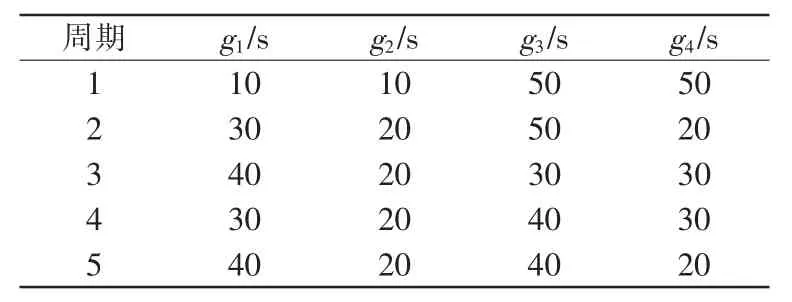

4 结语
