基于Matlab/Simulink的工业机器人力控制仿真研究

黄小翀，倪受东

（南京工业大学 机械与动力工程学院，南京 211800）

随着“中国制造2025”的提出，工业机器人已经广泛地应用于工业生产领域之中，机器人力控制是工业机器人研究的一个重点方向。当机器人手臂在执行与作业环境有接触的操作 （如焊接或者打磨）时，在特定的作业环境，机器人要求任意产生的作用力具有较高的柔顺性和机器人在自由空间作业时对位置伺服以及机械结构要求高强度的刚度之间存在矛盾，然而可以运用合适的控制方法来控制机器人与作业环境之间的接触力，能够有效地解决这一矛盾。

在机器人的力控制中，根据其运动特性可以归为四大类：阻抗控制策略、力/位混合控制策略、自适应控制策略和智能控制策略[1]。本文在工业机器人的力控制研究中采用阻抗控制的方法。阻抗控制算法是一种通过间接地方式去解决机械臂力/位置控制。通过控制机械手臂末端位置偏移量的方式间接的控制末端执行器与环境之间的接触力。在力觉控制算法中，Hogan提出的阻抗控制占有重要的地位，可以很好地将运动轨迹和力控结合在一个动态系统中。这样可以大大简化位置和力控制的复杂控制策略，并且能够消除环境变化和扰动带来的影响。阻抗控制的特点是利用间接的方式对机器人与环境的作用力进行控制，根据位置（或速度）与机器人末端的作用力之间的关系，通过调整系统反馈回来的位置误差、刚度或速度误差，以此达到控制力的目的[2-4]。同时，接触过程的弹性变形显得特别重要。所以，狭义地称为柔顺性控制。这一类型的力控制主要有位置和速度2种基本形式。通过将力反馈信号转换成位置调整量的方式，通常叫做刚度控制的力控制;通过将力反馈信号转换成速度调整量的方式，通常叫做阻尼控制的力控制;通过将力反馈信号同时转换为速度和位置两者的修正量的方式，叫做阻抗控制[5]。

目前实际应用中，大多数用的都是速度环控制反馈和位置环控制反馈相结合的力控制，而阻抗控制在两者基础上加入了力反馈。通过将阻抗控制运用到机器人柔顺控制中，可以改善传统的末端位置不准确。同时，在一些对末端位置和末端力矩要求严格的实际应用中，提供了更好的控制方法。所以，采用阻抗控制的方法，可以有效地控制机器人的力矩，从而提高机器人末端的位置精度。

1 工业机器人结构及仿真模型

1.1 工业机器人结构

六自由度工业机器人由6个旋转关节组成。其结构模型如图1所示。

图1 工业机器人结构Fig.1 Industrial robot structure

其中，大臂、前臂、小臂都为旋转关节，且运动在同一个平面内，关节运动之间具有连续性、相关性等。为了方便研究，本文将六自由度的工业机器人简化成二连杆机构，了解其运动特性，并对其进行动力学分析及仿真研究。

1.2 机器人动力学分析

二连杆机构示意如图2所示。

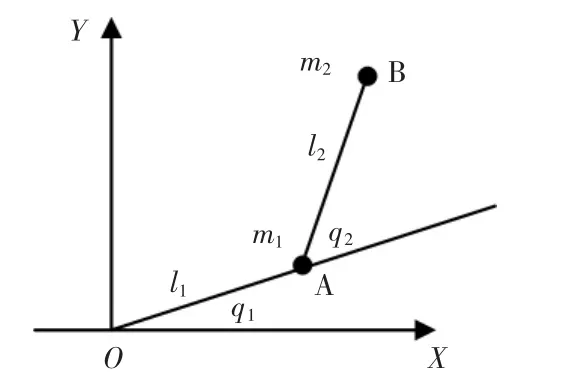
图2 机械臂示意Fig.2 Mechanical arm diagram

图中，机械臂1的质量为m1，长度为l1，夹角为q1；机械臂 2 的质量为m2，长度为l2，夹角为q2。 （角度顺时针为负逆时针为正）

如图2所示，由数学几何方法可以得机械臂2末端B位置的坐标为

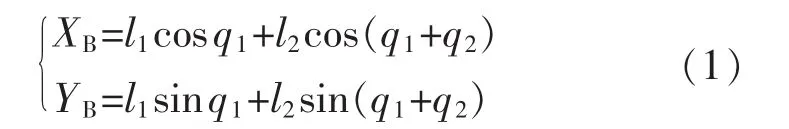
由式（1）可以求出雅可比矩阵为

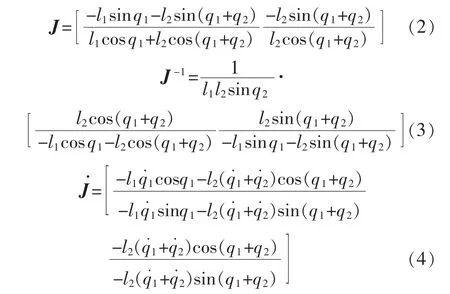
n自由度的机器人动力学方程为[6]

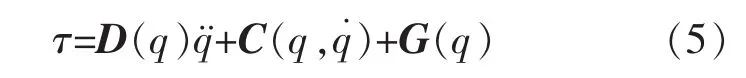
式中：D（q）是n×n为正定对称矩阵；是n×1的离心力和哥氏力矢量；G（q）是n×1的重力矢量；q为关节位置；τ为关节驱动力矩。

由拉格朗日方程式得：

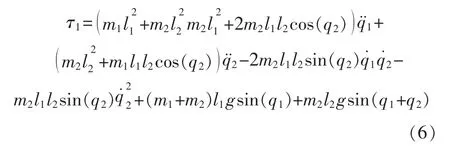
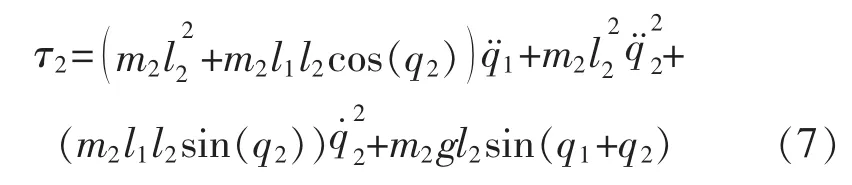
结合式（5）～式（7）可得出二自由度机械臂的惯性矩阵、离心力哥氏力矢量、重力矢量如下：

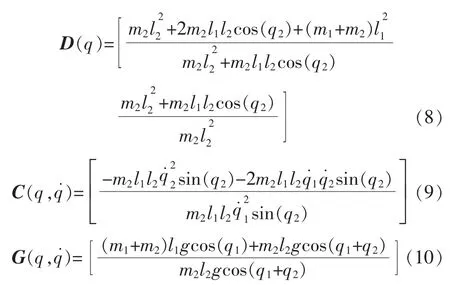
1.3 阻抗控制律分析

当处于受力空间是机械手臂受到环境的作用H（q，q˙）=C（q，q˙）q˙+G（q）力，令其动力学方程可以表示为

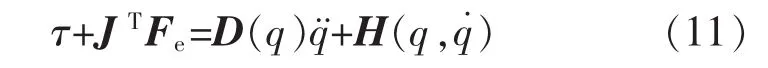
阻抗控制关系：

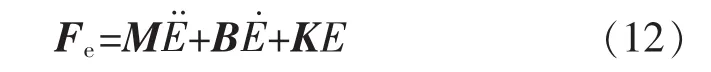
式（12）中，Fe是与环境接触作用产生的真实力。M，B，K分别为机械手目标惯性矩阵、阻尼矩阵、刚度矩阵，E=Xe-X表示手臂目标位置和当前位置的位移。

为实现上述的目标控制，采用式（13）的阻抗控制律[7]：

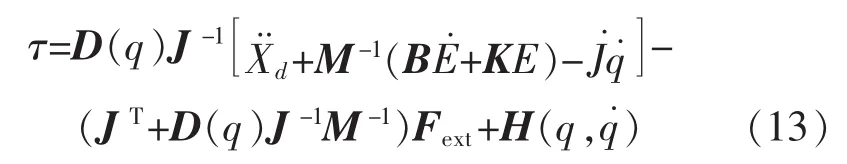
由控制律公式（13）得到此算法的原理框图如图3所示。

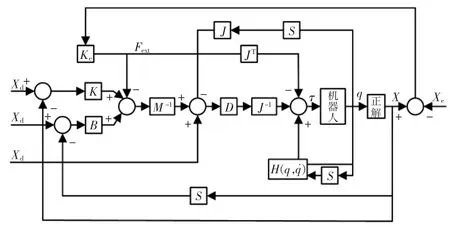
图3 阻抗控制算法的原理框图Fig.3 Principle block diagram of impedance control algorithm

2 阻抗控制系统参数选取及仿真

2.1 搭建控制系统

根据图3阻抗控制算法原理框图搭建控制系统仿真平台，输入信号是正余弦信号和反馈回来的实际位置信号做比较，得到差值E。输入信号经过微分处理和反馈回来的速度信号做差得到速度差值E˙。分别通过增益环节乘以M-1K，M-1B，再加上Xd的二阶导数和-J˙θ˙，再通过S函数，在S函数中乘以D（θ）J-1计算出扭矩，再加上离心力、哥氏力、重力引起的关节力矩h（θ，θ˙），从而求得加载在机器人关节上的扭矩 τ＝［τ1，τ2］。作为 ROBOT 的输入信号，调用S函数进行动力学逆解，求出相应的角度、角速度反馈给输入信号。在Simulink仿真平台搭建控制系统如图4所示，仿真中采用定步长，Runge（ode4）算法[8-10]。

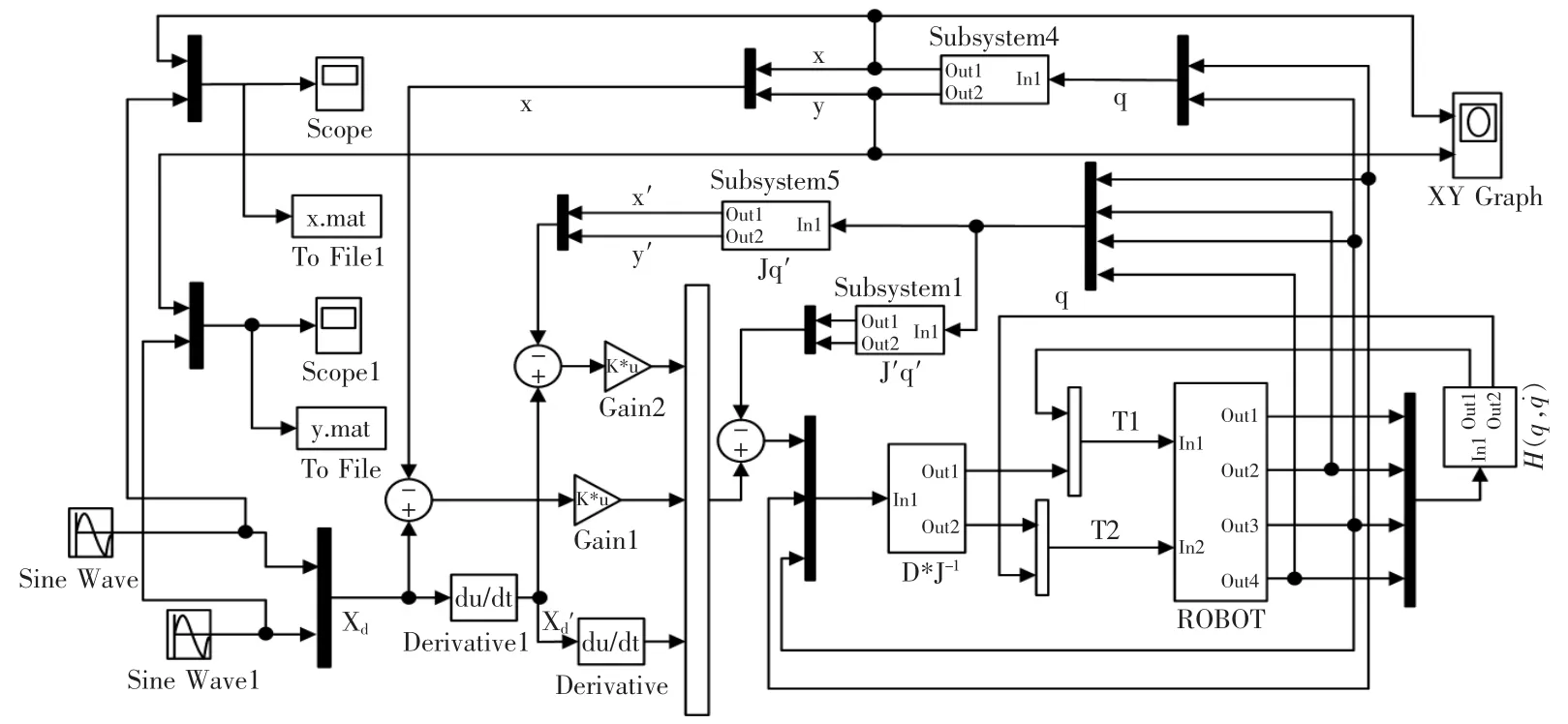
图4 阻抗控制算法仿真平台Fig.4 Simulation platform of impedance control algorithm

仿真平台ROBOT控制部分主要程序如下：

2.2 参数的选取以及仿真结果

将正弦信号同时接入到连杆2末端位置的XY方向上，为了简便接下来的仿真过程，只需考虑X方向上输出的跟踪信号，分析输出信号的响应曲线，就可以调整出相应的惯性系数，阻尼系数，刚度系数。时间从0～3 s，仿真步长设置为固定0.001 s[11]。

通过以上方法得出一组最佳系数如下：

M=I（I为单位矩阵）；

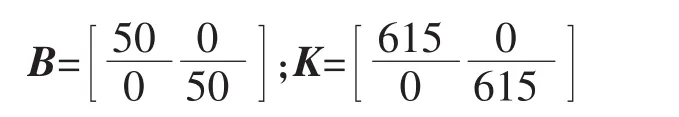
设l1=1 m，质量m1=1 kg；l2=1 m，质量m2=1 kg。两个关节的角位置变量分别是（π/3，π/6），两个关节的速度（0，0）均为零，它的末端位置P（0.866，1.5）。以下的仿真实验中选取惯性系数值M=1，阻尼系数值B=50，刚度系数值K=615。假设没有与外界环境作用，机械手作用力0，现在分别在机械手末端输入信号X=cost；Y=sint，XY的末端轨迹是以（0，0）为圆心，半径为1的圆。仿真步长设置为0.001 s，时间10 s。机械臂末端X、Y以及XY的轨迹图和XY的误差分别为图5～图8所示。

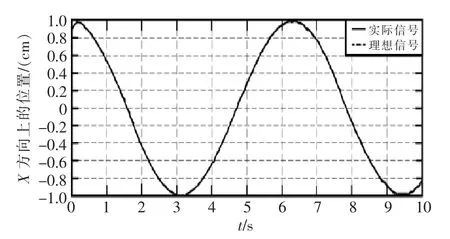
图5 X方向上的跟踪情况Fig.5 X direction tracking

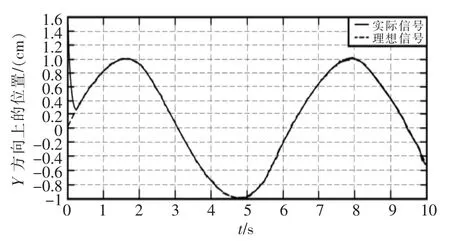
图6 Y方向上的跟踪情况Fig.6 Y direction tracking

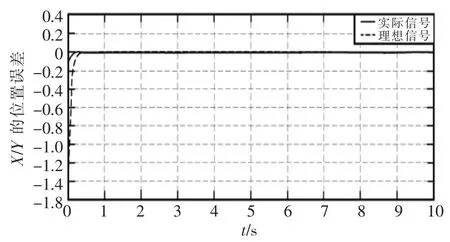
图7 X/Y的误差分析Fig.7 Error analysis of X/Y

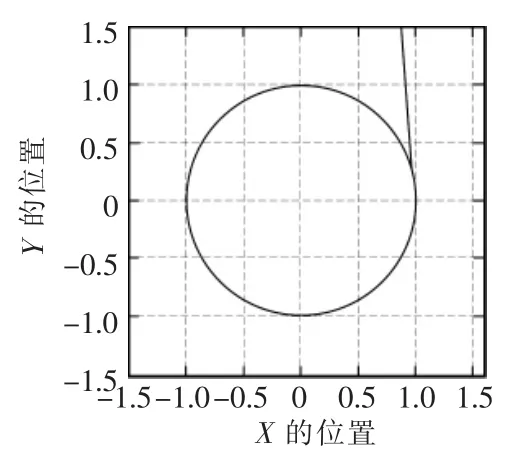
图8 末端的运动轨迹Fig.8 Terminal trajectory

由图5、图6可知，在X和Y方向上，分别在0.263 s，0.356 s已经可以跟踪上给定的信号轨迹，随后X、Y方向的误差几乎接近0，说明阻抗控制算法在消除机器人手臂末端位置的误差有显著的作用，能够提高位置控制精度。

3 结语

通过在Matlab/Simulink环境下进行阻抗控制算法的机器人力控制仿真，借助Simulink强大的S-Function进行控制程序编写，实现阻抗控制算法的仿真实验。从以上仿真结果可知，在X和Y方向上，都在短时间内跟踪上期望的信号轨迹。相比传统的力控制可以保证更高的精度，从而得出阻抗控制算法可以有效的消除控制误差，在机器人力控制上的应用可以提高机器人末端的位置精度。以后可以延伸到三自由度甚至更多自由的机器人，同时也可以通过Matlab/Simulink进行自适应控制，模糊控制等方法的仿真实验。