基于分层型的改进粒子群优化算法

安无恙，吕柏权，李 嫽

（上海大学 机电工程与自动化学院，上海 200072）

粒子群优化算法PSO是一种基于生物群智能的随机启发式搜索算法。其思想来源于对鱼群，鸟群等生物群体捕食的行为观察研究[1]。PSO具有计算简单、可调参数少、容易实现、寻优能力强等优势[2]，但基本的PSO算法容易陷入局部最优，出现早熟收敛现象，导致优化精度不高，因此改进基本PSO算法显得尤为重要[3]。

本文针对粒子群的特点与存在的缺陷，基于函数映射到不同平面的特点，提出了一种基于分层型的改进粒子群优化算法。

1 基本粒子群算法

粒子群优化算法在求解优化问题时，每个优化问题都好比是在搜索空间中的每只鸟的位置[4]，将这些鸟都看作是单个“粒子”，每个粒子都有自己相应的位置和速度，以及一个由优化函数确定的相适应的值。在整个优化寻优的过程中，每个粒子都将以当前自身的最小值来跟踪其当前所有粒子的最小值，并在搜索的过程中向着最小值的方向前进，通过一次次迭代不断接近全局最小点[5]。

定义粒子所找到的当前自身的最优解为个体极值pbest；定义整个粒子群体找到的当前的最优解为全局极值gbest。在每一次迭代过程中，每个粒子将自己的当前值与其pbest进行比较，如果粒子的当前值比pbest小，则用该值代替pbest，否则pbest值不变，同时将pbest与gbest比较，如果pbest比gbest小，则用此值代替gbest，否则gbest值不变。

设在D维搜索空间中，有N个粒子，其中第i个粒子的位置是Xi=（xi1，xi2，…，xiD），其速度为Vi=（vi1，vi2，…，viD）。 记第i个粒子搜索到的历史最优位置为Pi=（pi1，pi2，…，piD），也称为pbest，整个粒子群体搜索到的最优位置为Pg=（pg1，pg2，…，pgD）， 也称为gbest。Knenedy和Eberhrt最早提出的PSO算法的位置和速度公式如下：

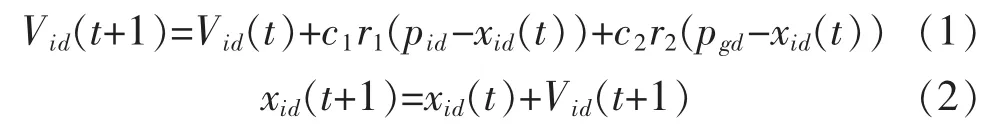
式中：i=1，2，…N；d=1，2，…，D；r1和r2是 2 个随机数，他们相互独立，服从［0，1］上的均匀分布；t则为当前迭代的次数；学习因子c1和c2为2个非负的常数，也被叫做加速系数，c1所作用的部分是粒子通过比较自身当前值与自身最优值，并不断向当前自身最优值靠近的过程，c2所作用的部分是粒子通过比较自身当前值与所有粒子的最优值，并不断向所有粒子的最优值靠近的过程，c1与c2合适的取值可加快搜索的收敛，而且不易陷入局部最优解。一般情况下c1和c2取2。为了控制xi和Vi跃出边界，需 要 进 行 限 制 ，xid∈［ximin，ximax］、vid∈［-vmax，vmax］，ximin为xid定义域中的x的最小值，ximax为xid定义域中x的最大值，vmax是之前设定的粒子的最大速率。

2 分层型粒子群优化算法的原理

分层型粒子群优化算法通过对粒子群进行旋转分层，增加粒子的多样性，将函数映射到不同的平面，从不同的角度和平面寻求函数的最优解。

假设该算法将粒子分为10层，每层10个粒子。在第一层的基础上，旋转α角或几个α角，形成第二层，在第二层的基础上，再旋转α角或几个α角，形成第三层，以此类推，形成10个粒子层。

要使一个层旋转，首先需要一个旋转矩阵。为了推导D维空间中的旋转矩阵，可以从二维以及三维旋转矩阵的推导入手，然后以此推出多维空间中旋转矩阵M的生成。

2.1 二维旋转矩阵

对于在二维平面内的向量，其在平面内只旋转了一个角度，而向量的模不变，如图1所示。

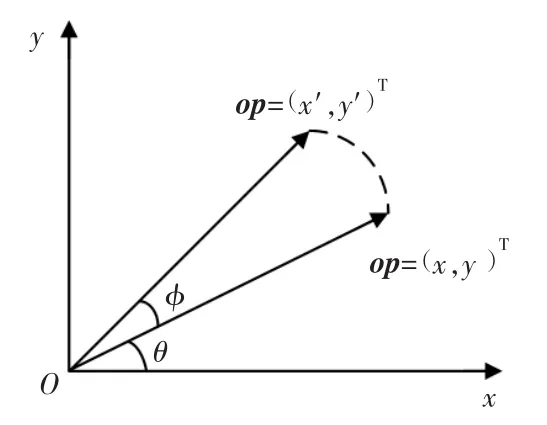
图1 二维平面内向量旋转Fig.1 Vector rotation in two dimensional plane

设向量OP的模为R，则可以得到旋转前所对应的坐标大小为

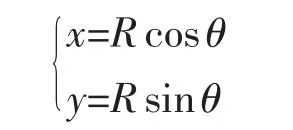
而旋转后的向量OP的模并没有发生变化，此时对应的横纵坐标变为

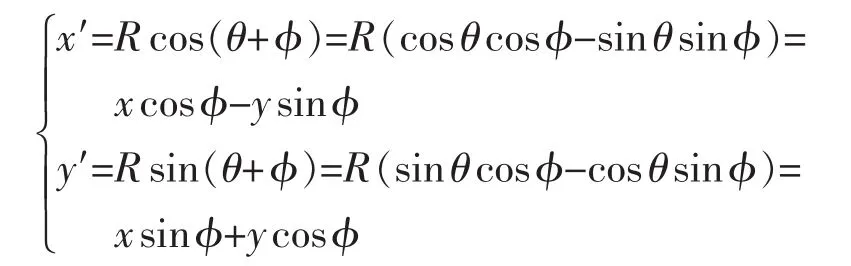
于是写成矩阵形式表示为

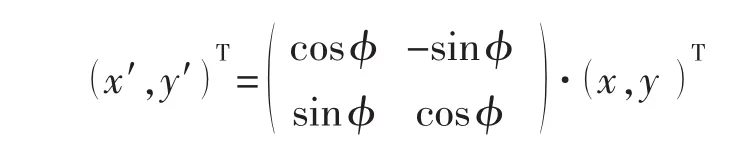
所以二维空间的旋转矩阵M可以表示为

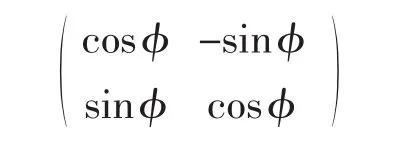
2.2 三维旋转矩阵

推导三维空间中旋转矩阵的表达形式，先考虑特殊情况，即以坐标系的3个轴为旋转轴的情况下向量的坐标变化情况。

如图2，当向量OP绕着x轴旋转时，其x坐标是不会发生变化的，产生变化的只是其在yoz平面上的投影位置，即对应的y、z坐标发生了变化。

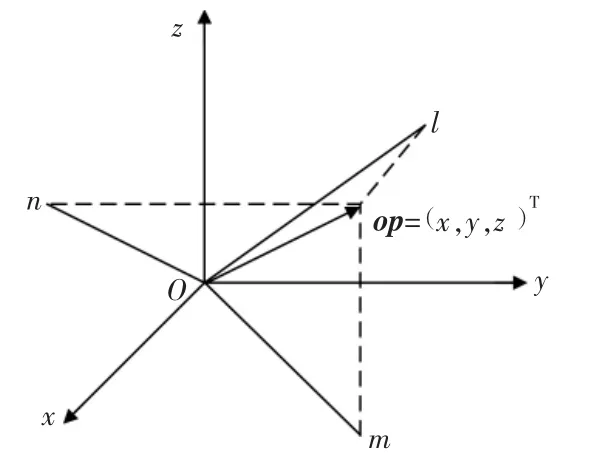
图2 三维空间内向量旋转Fig.2 Vector rotation in three dimensional plane

旋转前：

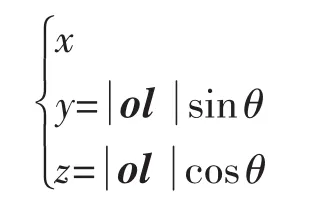
旋转后：

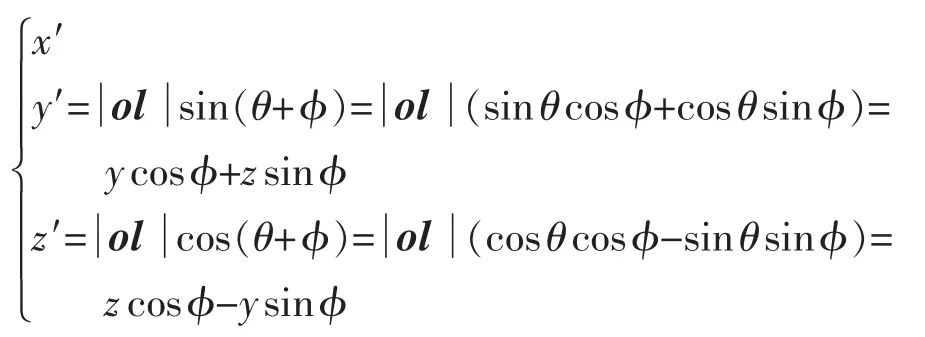
用矩阵形式可以写成：

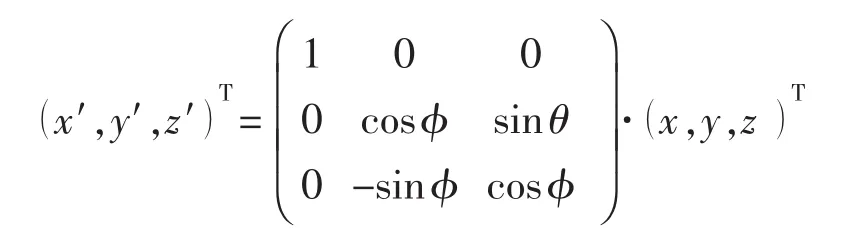
所以绕x轴旋转时的旋转矩阵：

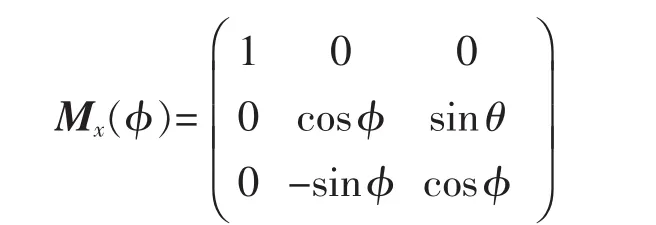
同理可以分别得到绕y，z轴旋转的旋转矩阵。三种情况下旋转矩阵分别为

根据欧拉旋转定理，任何一个角位移都可以分解为绕3个互相垂直的坐标轴的3次旋转，所以当三维空间里向量绕任意1个轴旋转时，可以表示成分别以x、y、z为旋转轴的旋转运动的叠加。

如果向量的旋转分解为绕着z轴旋转α角，绕着y轴旋转γ角，绕着x轴旋转角得到了旋转后的向量，总的旋转矩阵可表示为M=Mx（ β）·My（γ）·Mz（α）。

2.3 D维旋转矩阵

从二维和三维的旋转矩阵发现，在三维矩阵旋转时，当绕某一坐标轴旋转时，该坐标轴在旋转矩阵中对应的那一行列的向量不变，而在相应的位置中添加元素

二维空间向量是绕着1个点旋转，三维空间向量是绕着1条轴旋转，以此类推，四维空间是绕着1个平面进行旋转，即由2条互相垂直的坐标轴组成的平面。那么在D维空间里，当向量绕着某D-2个坐标轴所组成的空间进行旋转时，D×D维矩阵中D-2个行列的元素不变，相应位置中添加元素即代表了1次旋转。所以构建旋转矩阵的Matlab程序可以表示成如下：

上述每一次循环所产生的旋转矩阵即为D维空间中围绕由其中D-2个坐标轴组成的空间旋转随机角度RR所产生的旋转角，在每次循环的基础上乘上一个新的旋转矩阵代表了每一次旋转的叠加。上述语句代表着生成一个随机的D维空间的正交旋转矩阵在空间旋转一个角度α。

MM1=eye（D，D）；

MM2=（D21）*M1^（D20）*M1；%旋转

MM3=（D21）*M1^（D20）*MM2；%旋转

MM4=（D21）*M1^（D20）*MM3；%旋转

MM5=（D21）*M1^（D20）*MM4；%旋转

MM6=（D21）*M1^（D20）*MM5；%旋转

MM7=（D21）*M1^（D20）*MM6；%旋转

MM8=（D21）*M1^（D20）*MM7；%旋转

MM9=（D21）*M1^（D20）*MM8；%旋转

MM10=（D21）*M1^（D20）*MM9；%旋转

D20是一个正系数，表示一次旋转D20个α角，D21是缩放系数，适当的取值可以避免旋转后超出搜索范围。上述程序进行了10次旋转，在前一矩阵的基础上旋转D20个α角，依次旋转得到了10个不同角度的矩阵，起到了分层的效果。

用所在层的粒子随机产生的位置乘上该层的线性正交矩阵M得到新的位置，然后将所得位置值x代入优化函数计算出适应值。图3显示了一个二维函数有无旋转情况下的取值分布。可以发现旋转不会改变函数的结构，但增加了寻找的多样性。

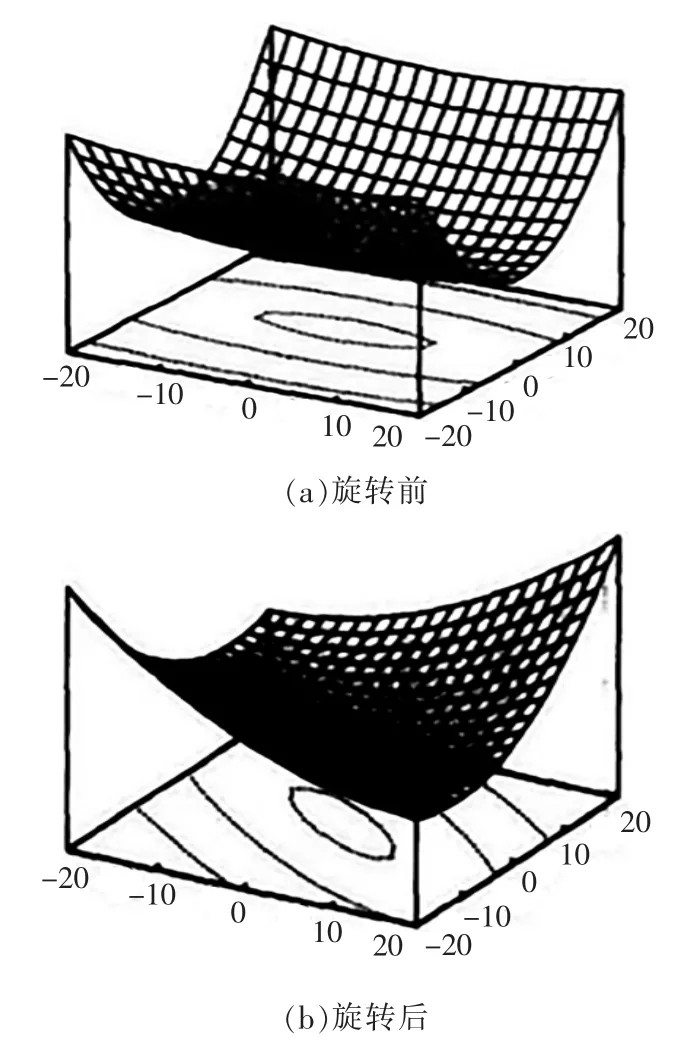
图3 曲面旋转前后情况Fig.3 Rotation result of curved surface

将目标函数分别映射到不同层上，在各个层搜索函数的最优解，将每层最优值与10层中找到的最优值进行比较更新，最终整个粒子群的全局的最优值。

粒子群的位置和速度更新公式如下：

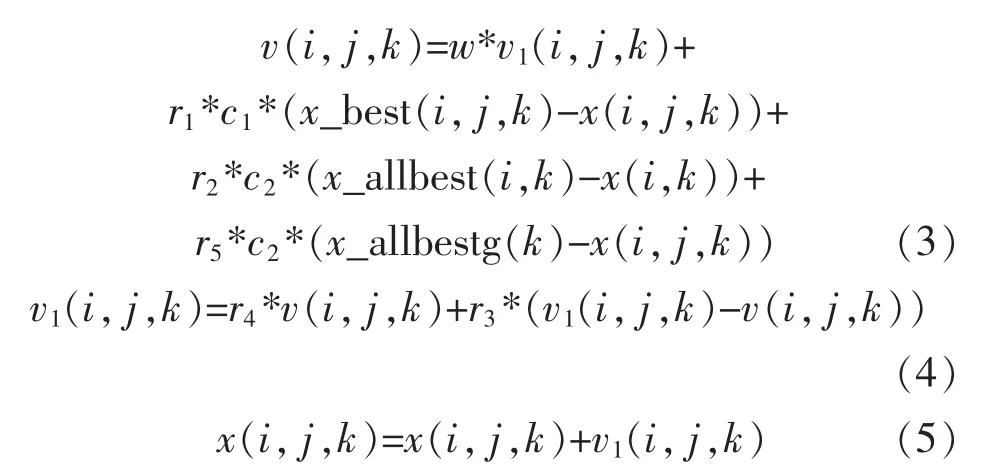
式中：i表示第几层；j表示第几个粒子；k表示在第几维空间；x_best（i，j，k）表示每个粒子的个体最优值，x_allbest（i，k）表示第i层的最优值，x_allbestg（k）表示整个粒子群的全局最优值。

3 分层型粒子群优化算法的原理

图4为粒子群优化算法流程。

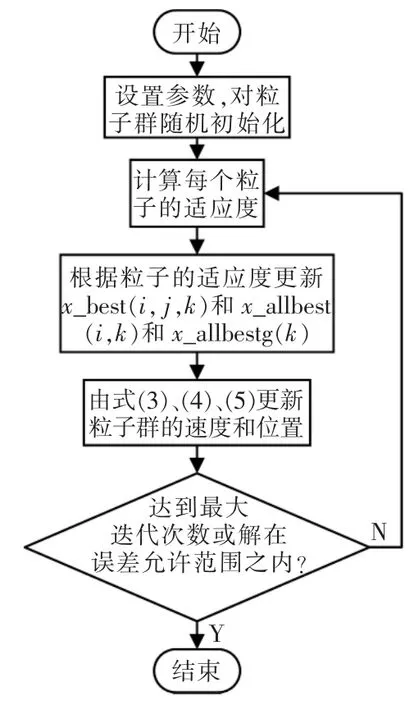
图4 分层型粒子群优化算法流程Fig.4 Flow chart of particle swarm optimization algorithm based on hierarchical

分层型粒子群优化算法流程：

（1）设置粒子群的层数和每层的粒子数和每个层的旋转角度，对粒子的位置和速度随机初始化。

（2）根据式（3）、（4）、（5）计算每个粒子的适应值。

（3）根据每个粒子的位置，更新个体历史最优位置x_best（i，j，k）。

（4）根据每个粒子的位置，将其适应值与该层内的所有粒子中最好的个体极值比较，如果更好，则将此位置设置为该层的全局最优值，更新该层最优值x_allbest（i，k）。

（5）根据每个粒子的位置，若适应值比整个群体的全局最优值更好，则将其位置设为整个群体的全局最优值，更新x_allbestg（k）。

（6）判断是否达到最大迭代次数或解在误差允许范围之内。若是，则x_allbestg（k）为全局最优值，否则，转至（2）。

4 仿真

在本文中，通过表1的基准测试函数仿真检验提出算法。

表1 基准测试函数（维数：30）Tab.1 Benchmark function（dimension：30）

4.1 仿真参数设置

用Matlab软件对上述9个基准测试函数进行仿真。分层型粒子群优化算法仿真参数初始值如表2所示。

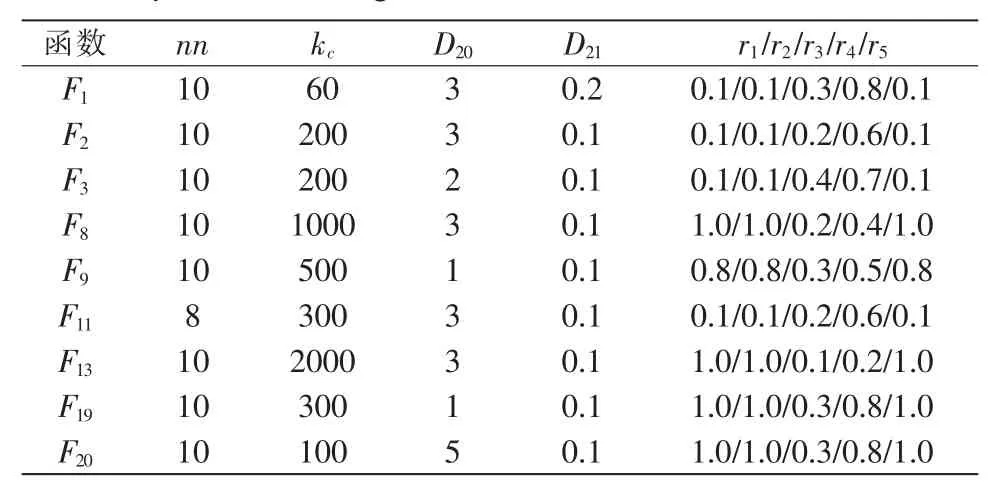
表2 分层型粒子群优化算法的参数初始值Tab.2 Parameter initial value of particle swarm optimization algorithm based on hierarchical

4.2 仿真试验结果

将上述9个基准测试函数作为测试函数，对每个基准测试函数都运行30次，统计每次运行的全局最优值结果及30次中成功收敛的次数，以及CPU运行的时间，在除去搜索失败的结果后，计算出每个函数成功收敛的最优值的平均值、最大值、最小值。为了比较算法在其他维数空间的性能优劣，分别在40、50、60维空间对每个基准函数都运行了一次，并把在四个维数空间运行的仿真曲线放在了一张图上。

表3是对9个基准测试函数的仿真结果。仿真结果显示：30个实验值全部成功搜索全局最优解，成功率为100%。

4.3 仿真试验迭代曲线

图5是对9个基准测试函数的仿真实验迭代曲线，各参数设置和初始值与前面相同，纵坐标表示搜索到的全局最优值，横坐标表示最大迭代次数。为了比较算法在其他维数空间的性能优劣，还对40、50、60维空间分别仿真了一次，将这4个维数空间的迭代曲线放在了1张图上。

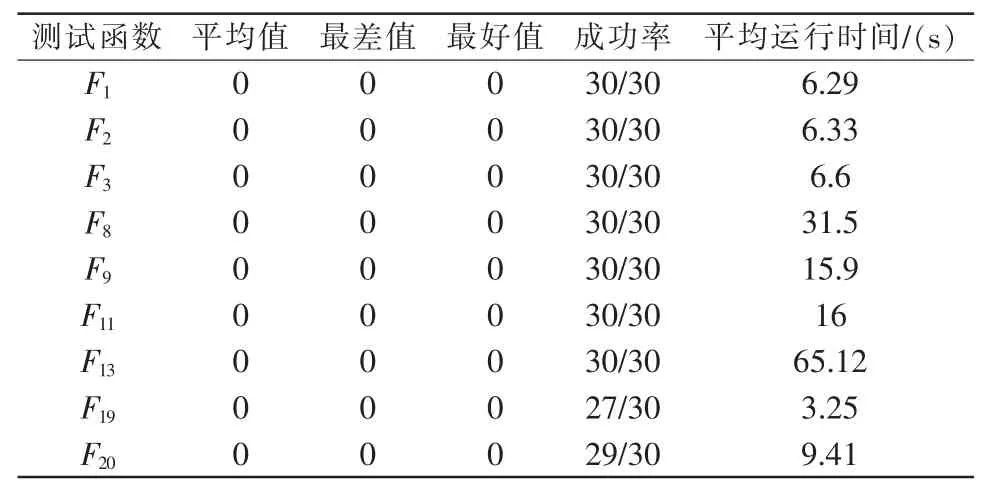
表3 分层型粒子群优化算法对测试函数的结果Tab.3 Test function results of particle swarm optimization algorithm based on hierarchical

从图中，可以发现虽然有些函数的搜索精度随着维度的上升而减弱，但是40，50，60维的精度还是与30维的精度相差无几，这说明了本算法的鲁棒性还是比较强的。

5 结语

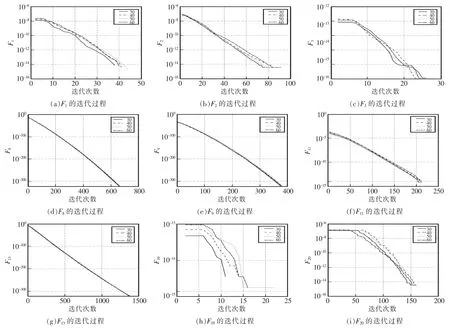
图5 仿真对比图Fig.5 Simulation contrast diagram

本文对于传统粒子群算法容易陷入局部极值点的问题提出了基于分层型的改进粒子群优化算法，通过旋转形成10个不同角度的粒子层，从不同的角度和平面求解函数的最优解，增加了粒子群的多样性，提高了搜索到最优点的可能性。并对9个基准测试函数在30、40、50、60维进行了仿真，从不同维度比较算法的搜索性能。从总体来看，分层型粒子群优化算法搜索性能较好。