基于旋转调制的惯导系统的误差分析与模拟∗
2018-07-31赵海军
王 旺 赵海军 姜 暖
(海军潜艇学院 青岛 266042)
1 引言
惯性导航系统的惯性器件误差通常包括陀螺漂移、加速度计零位偏置等,使得导航误差随时间不断积累。
为降低惯性器件误差对导航精度影响,国内对旋转惯性测量单元IMU在惯导系统中的应用进行了研究[1],结果表明,采用旋转可对惯性测量元件输出误差进行调制,提高系统精度。国外采用平台旋转方式改善系统性能的研究已成功应用[2]。文献[3~4]给出方位旋转平台惯导误差方程,通过旋转提高了加速度计零偏和东、北向陀螺漂移可观测度,同时有效抑制系统误差。
论文在上述研究成果的基础上,利用Laplace变换对单轴旋转惯性导航系统的误差进行了分析与仿真,结论表明,单轴旋转技术可有效抑制导航误差,提高导航精度。
2 单轴旋转惯性导航系统误差方程

单轴旋转惯性导航系统无阻尼误差方程为[3~5]式中,R为地球半径;g为重力加速度;we为地球自转角速度;w为单轴旋转角速度;δvx、δvy为东、北向速度误差;δφ、δλ为纬度、经度误差;ΔAx、ΔAy为东、北向加速度计零偏;α、β为水平失调角;γ为方位失调角;εx、εy、εz分别为东、北、方位陀螺常值漂移;εmx、εmy、εmz分别为东、北、方位陀螺随机漂移。
由误差方程可见,东、北向加速度计零偏和陀螺常值、随机漂移均受到旋转角速度的正余弦调制。
3 基于Laplace变换的惯性器件误差分析
为简化分析,暂不考虑傅科振荡周期,且令惯导系统处于静基座,由式(1),此时惯导系统的等效误差源分别表示为
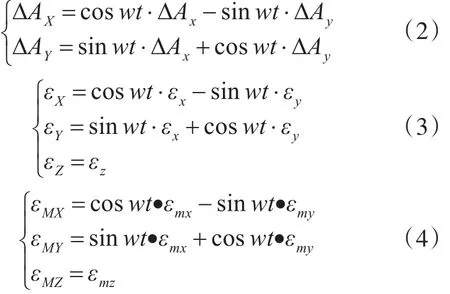
由式(2)、(3)可知,单轴旋转惯导系统,其等效惯性器件误差除方位陀螺常值漂移外,其余均为时变量,故不能作为常值简单处理。式(4)为等效陀螺随机漂移。
对式(2)、(3)作Laplace变换:
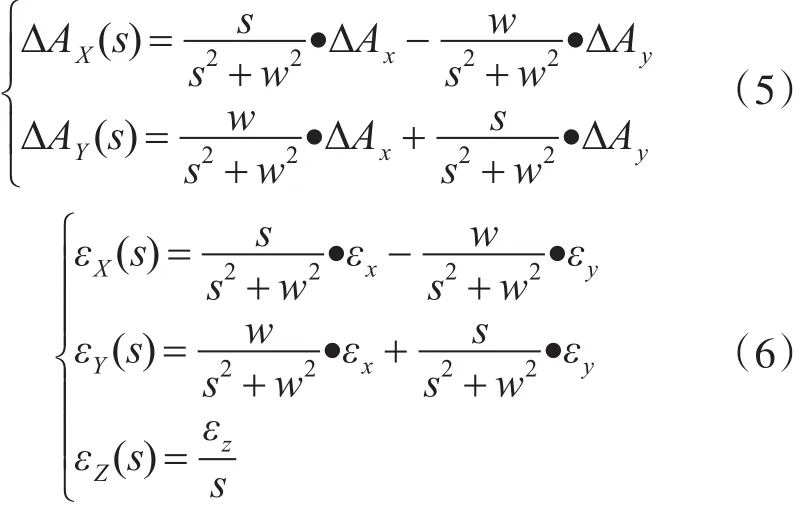
式中,s为Laplace算子。
由惯导系统误差原理可知,ΔAX造成系统东向速度误差及经度误差,则:

将式(5)中第一式代入式(7):

对上式作反Laplace变换,得:
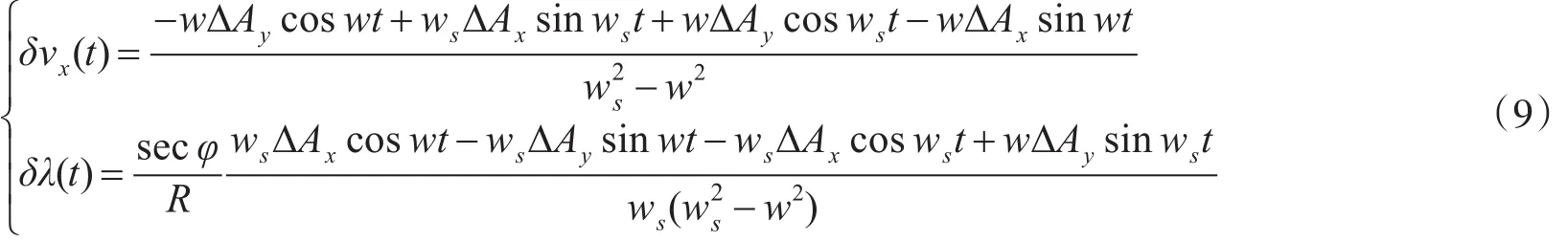
仅给出ΔAY、εX、εY、εZ对系统误差影响,推导过程从略。ΔAY对系统误差影响为

εX对系统误差影响为
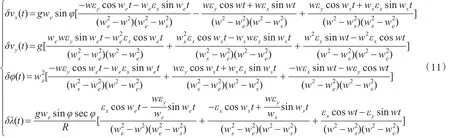
εY对系统误差影响为

εZ对系统误差影响为
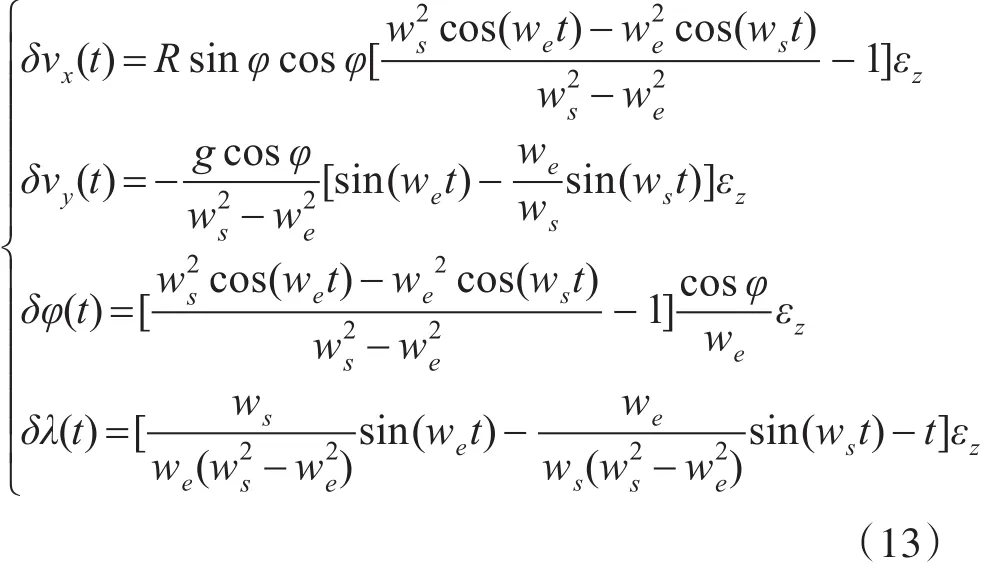
由式(9)~(13),单轴旋转惯导系统减少了随时间增长项及常值误差项。惯性器件误差对惯导系统速度、位置的影响大多为振荡性误差,振荡角频率包括we、ws以及w,同时伴随有常值误差和随时间增长的误差项。
4 旋转惯导系统误差模拟与仿真
仿真条件设定:载体速度为10kn,航向45°,载体初始位置φ=36°N、λ=122.2°E。
惯导系统参数设定:系统工作状态为水平阻尼;加速度计常值偏置ΔAx=ΔAy=6×10-5g;陀螺常值漂移:εx=0.02°/h,εy=0.02°/h,εz=0.02°/h;等效陀螺随机漂移:εmx=0.002°/h,εmy=0.002°/h,εmz=0.002°/h;令系统初始状态δvx=δvy=0,δφ=δλ=0,α=β=γ=0。单轴旋转角速度ω=60°/h。
所得系统速度、位置误差模拟结果如图1~4所示(图中,粗实线为旋转惯导,细实线为未旋转调制的惯导系统)。

图1 旋转惯导东向速度误差
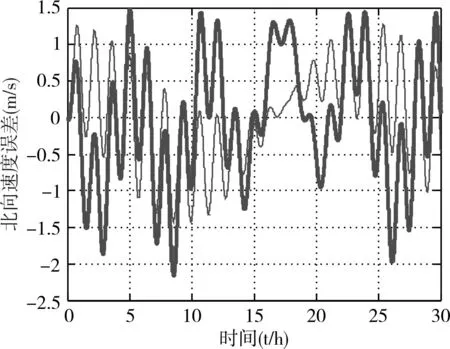
图2 旋转惯导北向速度误差
由图1~4可得出如下结论:
1)东向速度误差δvx的常值误差分量受北向陀螺漂移εy和方位陀螺漂移εz影响,由于北向陀螺εy受到旋转调制,故东向速度误差δvx的常值误差分量减小。
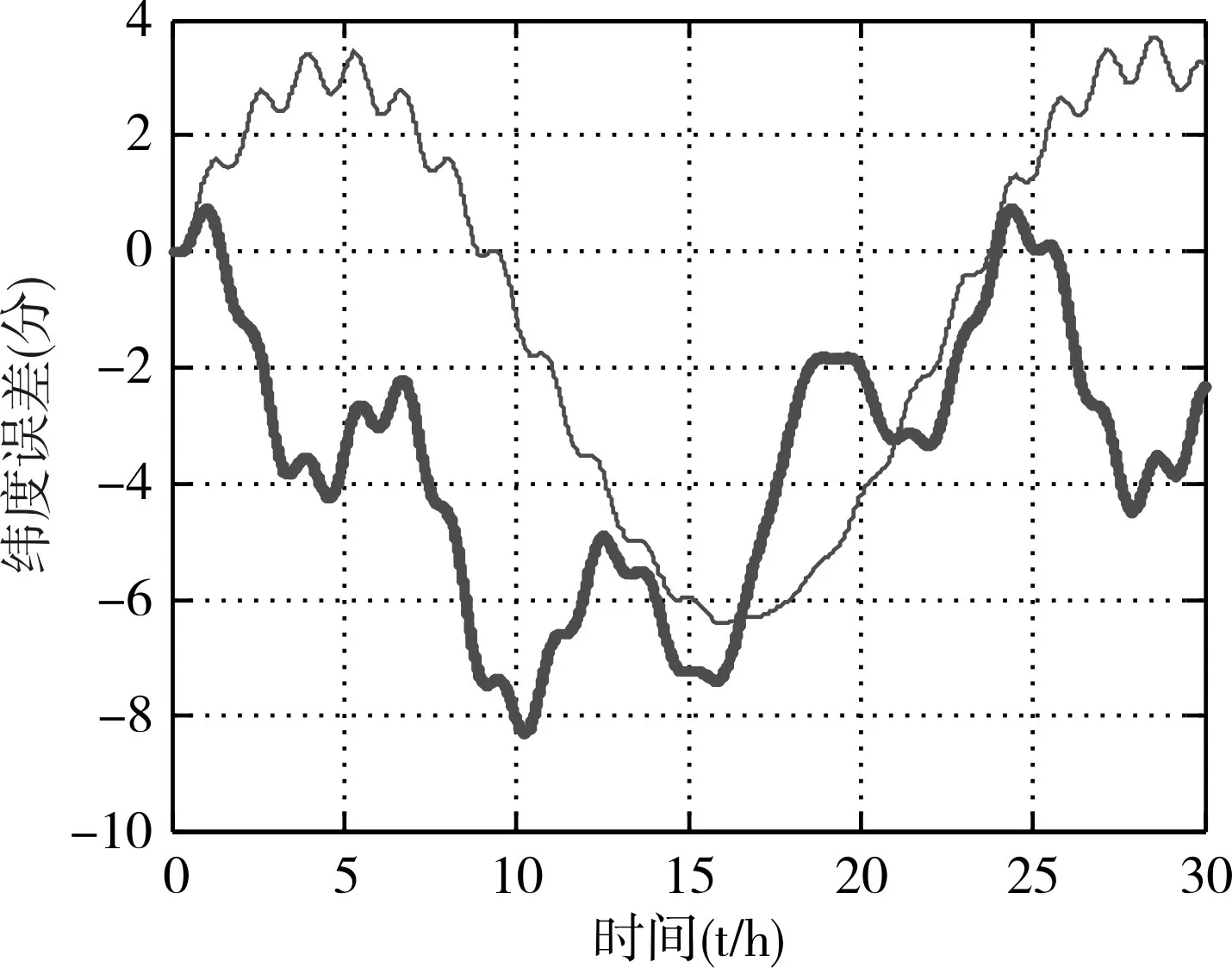
图3 单轴旋转惯导纬度误差

图4 单轴旋转惯导经度误差
2)纬度误差δφ,当北向陀螺εy受到旋转调制后,其常值误差仅受方位陀螺漂移εz影响。
3)由于东向陀螺漂移εx、北向陀螺漂移εy以及加速度计零位偏置ΔAx、ΔAy被旋转调制,故经度误差δλ常值误差分量和随时间增长的误差大大减小,发散速度明显降低。
5 结语
论文利用Laplace变换分析了惯性器件误差对旋转惯性导航系统的影响,并对其进行了模拟与仿真。分析与仿真结论表明,单轴旋转技术可有效抑制惯性器件误差影响,提高导航精度,为舰艇实现高精度的自主导航奠定了理论与实践基础。
