影响矩阵法在系杆拱桥成桥二次调索中的运用

徐传昶，鲁从森，王行耐

(1.山东高速工程检测有限公司，山东 济南 250002；2.中铁二十三局集团 第一有限工程公司,山东 日照；3.山东交通学院 交通土建工程学院，山东 济南 250357)

系杆拱桥具有自身特殊的结构特点，某些部件、构件的损伤在一定时间内不会导致结构整体破坏，难以在日常管养中发现，如吊杆力的损失，吊杆锚固体系的松动,混凝土结构随时间变化的收缩徐变,桥址周围桩基基础的不均匀沉降,以及施工期间遗留的质量隐患等，这些问题会随着运营期间不同外荷载作用下的叠加效应，对结构产生不利影响，导致结构损伤增加。调整系杆拱桥吊杆是后期改善结构内力的直接手段，对存在吊杆力损失严重的系杆拱桥进行吊杆力调整或换索，可以改善系杆拱桥整体内力。为使调索工作高效、合理，需严格控制调索过程。目前，国内多座系杆拱桥进行了施工期的二次调索，但是对系杆拱桥成桥运营期后的二次调索，实施系统地施工控制的工程实例较少。

调索的理论研究主要有最小二乘法[1]、最小弯曲能量法[2]、弯矩最小法[3]、影响矩阵法[4]等。最小二乘法是使求得的数据与实际数据之间的误差平方和最小，需要通过反复迭代的方式进行计算；最小弯曲能量法通过采用桥梁结构的弯曲余能为目标函数进行计算；弯矩最小法是把弯矩平方和作为目标函数进行计算。以上三种理论都应在结构分析中变化结构的模式，而影响矩阵法通过将优化的目标函数统一用索力变量与广义影响矩阵表示，能够同步对多个目标函数的优化，实现程序化计算非常便捷。

本研究采用影响矩阵法的理论[5-7]计算方法，对吊杆索力进行求解，确定合理的调索顺序,并以一座吊杆力损失严重的系杆拱桥为工程背景，验证影响矩阵法的应用，使全桥吊杆力达到设计索力的情况下同时满足结构的安全性，该方法具有方法清晰、简单、计算准确的特点。

1 运营期调索的影响矩阵法

1.1 影响矩阵法理论

受调向量是指控制断面上m个相互平行的独立因素构成的列向量。独立因素主要由控制断面内力或位移构成。在调整计算中均为受调元素，以便通过计算、调整达到预定的目标值。受调向量表示为：

D=(d1d2…dm)T。

施调向量是指通过调整可以影响受调向量的单一独立因素(1，2，…，m)所组成的列向量。记为：

X=(x1x2…xn)T。

施调因素大多为结构的内力、位移。

影响向量是指施调向量内第j个因素xj产生的单位变化导致受调向量D的变化向量，记为：

Ai=(a1ja2j…amj)T。

影响矩阵是指导致每一个施调向量产生的单位变化，引起的1个影响向量按顺序组成的矩阵组列，表示为：

(1)

影响矩阵的构成中，因素可以是内力或位移等多个向量中的任意一个，也可能是内力或位移的相互叠加影响。理论上只要将单位施调向量逐一施加到系杆拱桥分析结构上，逐一计算出对应的影响向量，把各影响向量拼合成结构的影响矩阵。

采用结构有限元法计算影响矩阵的步骤为：

1)形成调值计算阶段的结构总刚度，并进行三角化分解。

2)令j号施调元调整量为1(若为内力，则通过单位强迫变形实现)，形成相应的结构荷载向量，最后回代求对应的节点变形。

3)对受调元i循环，计算对应的受调因素di：若di为位移，则通过求解的位移向量，提炼出该调值点对应方向的位移作为j列影响向量的第i个因素aij；若di为内力，则通过位移向量分析出相应调值截面相应方向的内力作为aij；若di为应力，就由内力求出相应点的内力作为aij。

重复2)和3)步骤，便能得到所有影响向量，进而得到影响矩阵A。

若受调向量和施调向量的因素相同，此类调值分析是等变量的调值分析。在系杆拱桥结构为线性关系累加时为：

AX=D，

(2)

由式(2)可分析得到唯一一种施调向量X。若要控制断面力学参数达到D，就要使得施调向量产生X的对应的变化为：

X=A-1D，

(3)

通过进行影响矩阵的分析求解后，便能得到对应的索力施调量。在受调向量数n以及施调向量数m相同的情况下，可由式(3)求得单一一个施调索力向量X[8]。

1.2 系杆拱桥调索影响矩阵形成原理

成桥运营期的系杆拱桥的结构调索分析，其实是为了寻找一种最优的吊杆力调整方法。通过影响矩阵的调索计算方法，在满足多个目标的情况下，实现吊杆力调整的调整量和最优的调索张拉顺序[9]。

为使成桥运营期后吊杆力调整过程科学、快捷，需要计算得到一个最优的吊杆张拉顺序以及吊杆力调整量序列[10-18]，并且在整个调索施工过程中，内力、位移和吊杆力不能超过一定阈值的情况下，最终吊杆力达到目标值。以调索前的结构实际状态为结构初始状态。初始状态下的索力矩阵Tc、控制截面应力矩阵σc分别为：

Tc=[Tc1Tc2…Tcn]T，

σc=[σc1σc2…σcn]T

通过影响矩阵法计算得到吊杆力的影响矩阵为AT，AT是一个n×n阶的矩阵组列，矩阵中的元素ATij为j号施加单位力1的时候对i号吊杆力产生的响应值。设调索后的目标吊杆力为Tm，施工中需要调整的吊杆力向量为Ts，则有：

Tm=Tc+AT·Ts，

施工中需要调整的吊杆力

Ts=AT-1·(Tm-Tc)。

需要在施工中调整的吊杆力向量确定后，施工中无论先调整哪根吊杆力，只要按照求出的吊杆力调整值调整，均能达到预先设定的目标吊杆力。但是为了简便、科学、快捷，还是要根据求出的吊杆力调整值，确定一种最快捷的调索顺序，同时该调索顺序还需使得结构内力和位移为最优状态。

把吊杆在各个施工阶段对应的工况下产生的吊杆力作为目标控制函数，同时对各个施工阶段中结构对应产生的应力和位移设定一个变化范围，使得应力和位移在产生最小变化值的情况下，得到一个最合理的调索顺序X=[x1x2…xn]T。

建立一个单目标、多约束条件的求解问题：

得到X=[x1x2…xn]T,使得

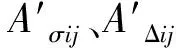
通过运用惩罚函数法[19]把以上所列的单个目标、多约束问题变成无约束的问题，最终得到一个最优的吊杆力施工顺序X[20]。

2 工程应用

2.1 工程概况

施调桥梁为跨径组合(24+36+24)m的下承式钢筋混凝土连续系杆拱桥。系杆采用预应力混凝土结构，吊杆布置在拱片内，主跨纵向设8对吊杆，边跨纵向均设5对吊杆，吊杆间距均为4 m。每对吊杆由横向间距为0.9 m的两根吊杆组成。本次调索计算采用有限元分析软件Midas Civil，全桥共504个节点，839个单元，其中803个梁单元，36个桁架单元，吊杆按只受拉桁架单元模拟。

a)桥梁立面图 b)有限元模型图图1 桥梁布置图

调索前吊杆力实测值见表1。

表1中的吊杆力实测值作为该桥调索前的索力。确定结构实际的索力状态后，在计算前把吊杆锚头位置作为关键控制断面，把锚头断面位置的初始位移值设定为零，初始应力为目前实际的应力。根据影响矩阵的方法就可以计算出该截面的应力、竖向位移的影响矩阵。

2.2 结果分析

施调大桥共36对吊杆，左右对称张拉，由式(1)方法得出吊杆力影响矩阵，吊杆力相互影响矩阵构成元素见表2。

表3为吊杆力调整后最终值与设计值比较。

表1 吊杆力 kN

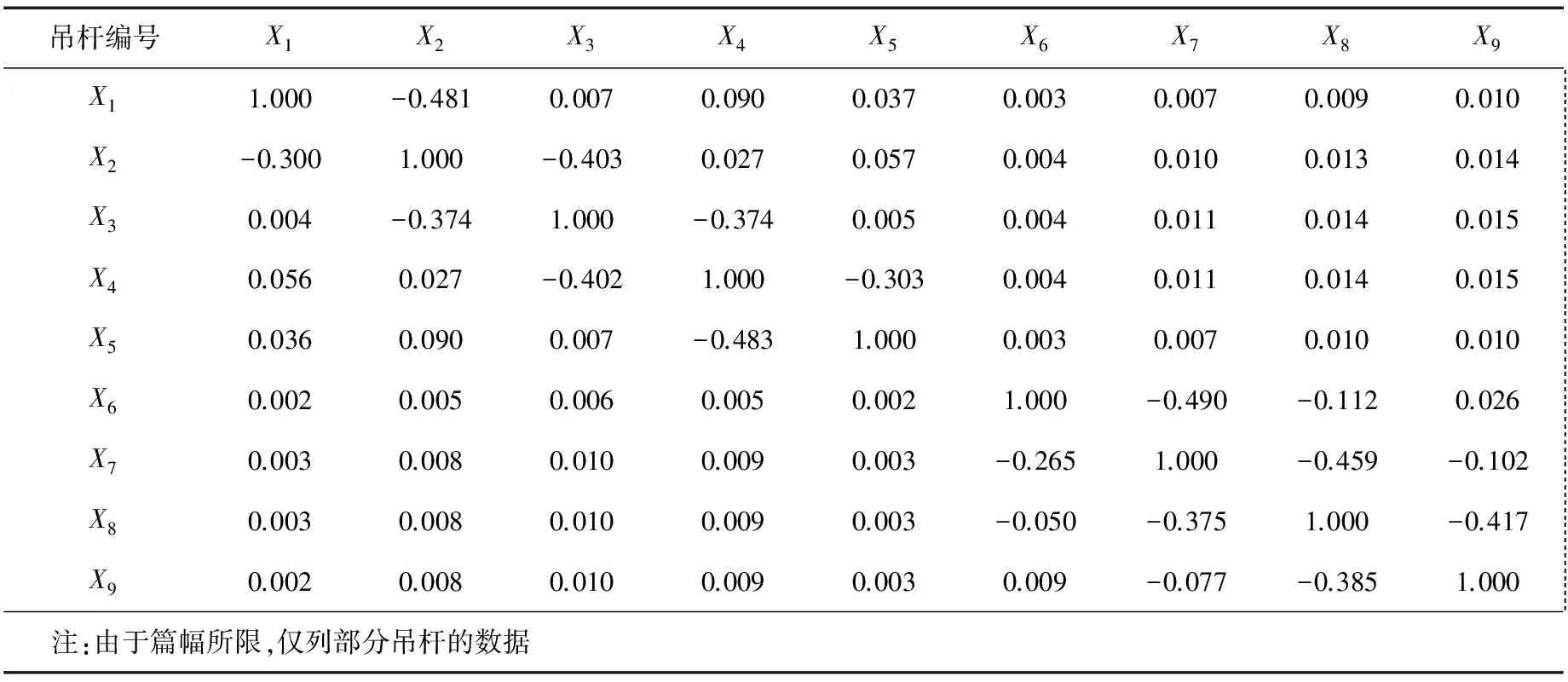
表2 吊杆力影响矩阵构成元素

通过以上方法进行了成桥吊杆力二次调整，调整后的成桥吊杆力的理论值与实测值相差均在±10%以内。

桥梁结构模型理论计算位移如图2所示。

调索前桥面线形较平顺，调索后各跨桥面起拱呈抛物线状分布，实测线形与模型计算结果吻合较好，见图3。跨中桥面抬高较明显，其中东侧中跨跨中实际抬高82.7 mm，略高于理论值(79.7 mm)；西侧中跨跨中实际抬高85.8 mm，略高于理论值(82.3 mm)。部分测点高程略微高于理论计算值是因为桥梁系梁存在斜裂缝，使桥梁整体刚度相较理论状态有所降低所致。

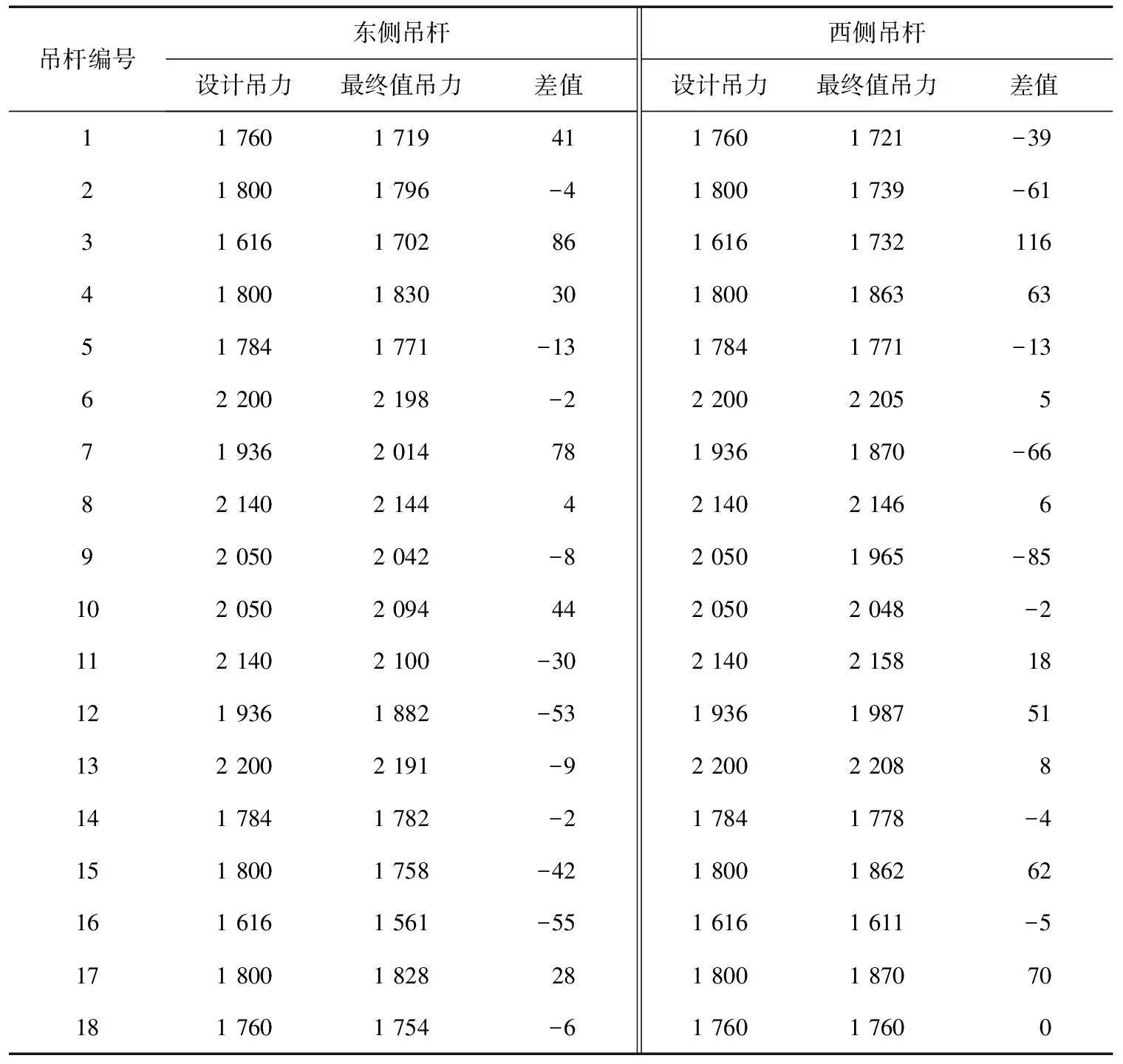
表3 吊杆力调整后最终值与设计值比较

a)调整前理论位移 b)调整后理论位移图2 调整前后理论位移变化图

a)东侧调索前后桥面线形 b)西侧调索前后桥面线形图3 调整前后桥面线形变化图

3 结语

本研究以影响矩阵理论为基础，建立了运营期系杆拱桥吊杆力调整数学模型，并在实桥吊杆力调整施工中进行监控，从整个调索施工过程中对受控变量的理论仿真结果和实测结果及其对比结果可以看出，桥梁调索过程中吊杆力控制结果较好，桥梁结构在施工过程中一直处于安全状态；桥面线形控制的精度比较高，且这些受控变量的量值在施工过程中变化的趋势与理论值趋势相一致，监控效果理想。本研究成果为运营期系杆拱桥吊杆力调整计算提供了一定的参考，同时为下一步深入研究运营期系杆拱桥索力调整监控提供了一定的借鉴。