重型汽车动力总成悬置系统解耦设计

孙志刚，徐伟刚，王军，刘保国

(中国重型汽车集团有限公司 技术发展中心，山东 济南 250101)

汽车动力总成悬置系统由弹性支承和刚性支架组成，用于动力总成的支承和定位，减小动力总成与底盘之间的振动传递等。通过合理设计悬置的角度和刚度，使其在满足可靠性要求的基础上，与车架之间的振动传递率较小，并使悬置系统具有较高的振动解耦程度[1-2]。系统在某个广义坐标方向上解耦，就是沿着该方向的激振力只能引起该方向上的振动，即沿着该方向的激振力所做的功全部转化为该方向的能量。系统的解耦程度通常用解耦率表示，解耦率是指在某阶模态振动时某个广义坐标的振动动能与所有广义坐标的振动总动能的比，当比值达到100%时，系统在该模态振动下是完全解耦的。解除动力总成的6个自由度之间的振动耦合，一方面便于减小可能激起共振响应的频带宽度，另一方面便于合理配置悬置系统的固有频率，使激励频率远离固有频率，从而获得良好的隔振效果。因此，解除多自由度振动耦合是动力总成悬置系统设计的一个重要目标。在工程实践中，重型汽车动力总成悬置系统是按发动机和常用变速器的配置进行设计，悬置系统一般由四点支承，但在某些特殊情况下车辆要求装备缓速器等附加配置时，若用四点支承的悬置系统，在车辆运行过程中悬置系统受力不平衡，容易发生悬置的螺母松动、橡胶块损坏等故障。本文在变速器后部增加一个辅助悬置，计算带有辅助悬置的悬置系统刚度，以实现悬置系统的良好解耦，使动力总成在作刚体运动时6个自由度之间的相互影响降至很小。

1 动力总成悬置系统设计

1.1 悬置系统固有频率配置要求

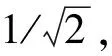
以重型汽车匹配的六缸四冲程柴油发动机为例，点火脉冲频率

式中：n为曲轴转速，r/min；i为发动机气缸数,i=6；τ为发动机冲程数,τ=4。

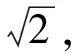
实现动力总成刚体振动模态解耦是悬置系统设计的重要目标，重点应实现动力总成在垂直和侧倾方向之间，以及垂直和俯仰方向之间的解耦。

1.2 动力总成悬置系统动力学分析

动力总成悬置的弹性元件为橡胶块，橡胶块在空间三维方向上都有弹性，但各个悬置的间距比悬置本身的尺寸大得多，由单个悬置本身的角刚度产生的力矩比由各个悬置联合产生的力矩小得多，因此单个悬置的角刚度可以忽略不计，同时因振幅较小，阻尼也可忽略，所以可将单个悬置简化为沿3个弹性主轴的无阻尼线性弹簧[5]。动力总成悬置系统固有频率范围内动力总成只存在刚体模态，因此可以把动力总成简化为一空间刚体，其位置可用质心的3个直角坐标x、y、z，以及绕质心平行于定坐标轴的3个动坐标轴转角θx、θy、θz表示，因而动力总成具有6个自由度，其广义坐标列矢量

动力总成振动系统定坐标系原点在平衡位置时的质心上，x轴平行于曲轴轴线指向车辆后方，z轴平行于各气缸中心线指向发动机上方，y轴垂直于x、z轴指向车辆左侧(面对汽车前方看)。

1.2.1 动力总成振动动能

动力总成动能Ek为质心平动动能Ekp与绕质心的转动动能Ekr之和，即

式中：m为动力总成的质量；Jx、Jy、Jz分别为动力总成绕对应坐标轴的转动惯量；Jxy、Jyz、Jzx分别为动力总成对应坐标的平面惯性积[6]。

工程上需要将实际复杂系统作一定的简化，建立既能反映实际系统的动力学特性又便于计算的动力学模型，根据实际可将定坐标系的3个坐标轴近似为动力总成惯性主轴，此时Jxy=Jyz=Jzx=0。

图1 动力总成悬置系统布置示意图

1.2.2 动力总成振动势能

不计动力总成自身在重力场中势能的变化，实际动力总成悬置的弹性主轴分别与定坐标系对应的3个坐标轴平行，按动力总成悬置系统带有辅助悬置，左前、右前、左后、右后和辅助悬置依次编号为1～5，如图1所示。它们沿3个弹性主轴方向的刚度分别为kxj、kyj、kzj,(j=1,2,……，n，n为悬置点的数量)。各支承处的坐标为xj、yj、zj，可推导出系统势能Ep为：

1.2.3 系统振动微分方程

已知拉格朗日方程

式中：qj为系统的广义坐标(即x、y、z、θx、θy、θz)；T为系统的动能；V为系统的势能。

将系统的Ek、Ep代入拉格朗日方程，整理得到关于6个广义坐标的微分方程组

(1)

将式(1)写成矩阵的形式，有

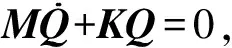
(2)

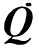
式(2)为典型无阻尼多自由度振动系统微分方程，可以求出系统的固有频率和主振型。

1.2.4 系统弹性解耦方程

式(1)中的每个微分方程包含多个广义坐标，解耦就是要使每个微分方程的广义坐标仅为一个，即质量矩阵和刚度矩阵都成为对角阵。解耦有利于单独对系统的某一广义坐标进行优化设计而与其它广义坐标互不影响。例如为使式(1)相对于广义坐标z解耦，令式(1)中第3个式子的弹性耦合项为零，即

(3)

使式(1)中第3个式子变成

(4)

此时式(4)只包含广义坐标z，因此实现了式(1)对于广义坐标z的解耦。

式(3)中因广义坐标θx、θy一般不相等且不为零，则有

按上述方法同样对另外5个广义坐标x、y、θx、θy、θz进行弹性解耦，整理后得

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

式(5)～(13)即是动力总成悬置系统弹性解耦方程，其中式(5)为x与θz解耦，式(6)为x与θy解耦，式(7)为y与θx解耦，式(8)为y与θz解耦，式(9)为z与θy解耦，式(10)为z与θx解耦，式(11)为θz与θx解耦，式(12)为θx与θy解耦，式(13)为θy与θz解耦。根据式(5)～(13)可计算动力总成悬置的刚度，实践中可根据具体情况灵活运用，本例中动力总成各支承处的坐标相对于oxz平面对称，左前与右前、左后与右后悬置在3个弹性主轴方向上的刚度相同，因此可知式(5)(10)(12)和(13)式恒等于零。当式(5)～(13)无法同时满足时，工程上重点关注发动机及路面的主要激励方向x与θy、y与θx、z与θy之间的解耦，使kxj、kyj、kzj满足式(6)(7)(9)。

1.3 动力总成辅助悬置

在设计实际重型汽车动力总成悬置系统时，首选四点悬置系统。一般按照最常用变速器(如铝壳12挡变速器)的配置输入惯性参数，各悬置点的坐标在发动机设计时已经确定，然后根据悬置系统固有频率要求和弹性解耦要求，并结合企业相关经验，可得出四个悬置点的各向刚度，如表1所示。前后悬置结构见图2、3。

表1各悬置点的主轴静刚度N/mm

悬置点kxkykz左前1100330890 右前1100330890 左后16105001310 右后16105001310

图2 前悬置结构 图3 后悬置结构

在匹配更长更重的变速器(如铁壳16挡变速器)、带取力器或缓速器时，原有四点悬置系统可能不满足使用要求，此时需要在变速器后部增加一个辅助支承。根据一般动力总成悬置的设计要求，发动机缸体后端面静弯矩不得高于设计的允许值，否则就应该增加辅助支承。

发动机缸体后端面静弯矩

Mx=mtgL5-(megL1L3+mtgL4L3)/L2，

(14)

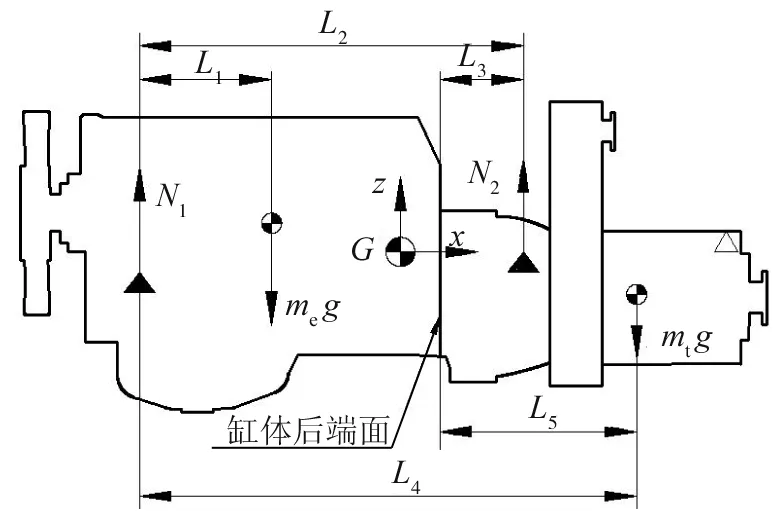
图4 重型汽车动力总成悬置系统受力图

式中：me为发动机质量；mt为变速器质量；g为重力加速度，g=9.8 m/s2；L1～L5见图4标注。

将测量得到的实际质量和尺寸参数代入式(14)可计算出Mx=1 466 N·m，大于发动机缸体后端面设计允许静弯矩，因此本例有必要在变速器上增加一个辅助悬置。

1.4 基于弹性解耦的辅助悬置刚度设计

根据本例动力总成辅助悬置的结构特点，辅助悬置不限制动力总成y方向上的小幅运动，即ky5=0，最后归结为解式(6)(9)，求出kx5和kz5。

动力总成振动系统定坐标系原点在平衡位置时的质心(见图4的G点)上，根据实际模型测量得到的各个悬置点的坐标见表2；利用称重和扭摆法测量得到各惯性参数：m=1 643 kg，Jx、Jy、Jz分别为76、360、330 kg·m2。通过式(6)(9)求出辅助悬置x向静刚度kx5=717 N/mm，z向静度kz5=644 N/mm，辅助支承的结构及其橡胶块的结构见图5、6。

表2各个悬置点的坐标mm

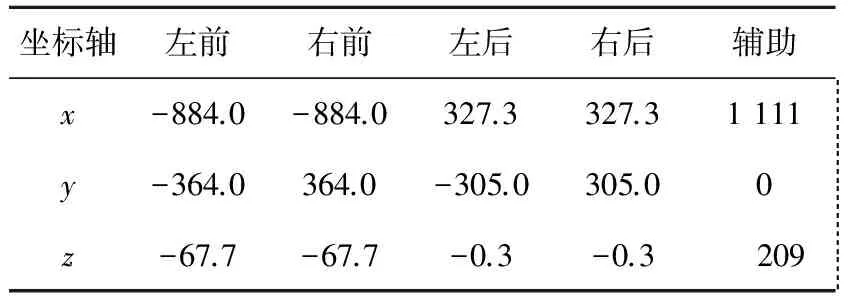
坐标轴左前右前左后右后辅助x-884．0-884．0327．3327．31111 y-364．0364．0-305．0305．00 z-67．7-67．7-0．3-0．3 209

图5 辅助支承结构 图6 橡胶块结构

与金属弹簧不同，橡胶弹簧在承载变形时有较大的迟滞性，其动刚度比静刚度大[7-9]，动刚度与静刚度的比值称为动态系数d。d与频率、振幅、温度、橡胶硬度和承载方式有关，一般压缩时d=1.4～1.7，剪切时d=1.3～1.5。本例橡胶悬置静刚度试验表明，在静变形为±7 mm范围内，静刚度接近于线性，随着变形的增加，静刚度逐渐增大。橡胶悬置动刚度试验表明，在测试频率为0～50 Hz时，随着测试频率的增加，动刚度基本呈线性增加趋势，增幅为10%左右；在测试振幅为±0.1～±1 mm时，随着测试振幅的增加，动刚度呈线性减小趋势，减幅为7%左右。在激励频率为27.5 Hz、振幅为±1 mm时的动刚度是静刚度的1.3倍，因此本例辅助悬置的动态刚度可取值1.3，得到辅助悬置x向和z向动刚度kdx5=932 N/mm，kdz5=837 N/mm。

2 弹性解耦仿真分析

2.1 能量解耦法

动力总成振动时产生沿多个广义坐标的振动，激振力和力矩所作的功转化为系统沿多个广义坐标的动能和势能，由于系统沿某一广义坐标振动的动能和势能之和为一常数，因此只需取最大动能(此时势能为0)表示振动总能量，当系统以第j阶模态振动时，它表现出主振动，第j阶模态振动的最大总动能

(15)

式中：ωj为第j阶固有频率；φkj、φlj分别为第j阶主振型向量φj的第k个元素和第l个元素；Mkl为系统质量矩阵M的第k行、第l列元素；k、l、j=1,2，……，6。

因此当系统以第j阶模态振动时，第k个广义坐标所分配的动能占系统总动能的比值为

(16)

由式(16)可定义能量分布矩阵

(17)

矩阵γ的第j列第k行元素代表第j阶模态振动总动能在第k个广义坐标上分配的比例。可根据广义坐标所分配动能的百分比来判断坐标间的耦合程度，即某一广义坐标分配的动能占系统总动能的比值越大，系统在该模态下的解耦程度越高[13-15]。

2.2 ADAMS仿真分析

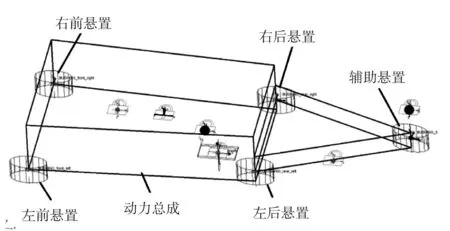
图7 动力总成悬置系统动力学模型

按动力总成质心坐标和各悬置点的坐标在多体动力学分析软件ADAMS/View中建立悬置系统动力学模型[16-18](见图7)，以一个具有6自由度的空间刚体表示动力总成，输入惯性参数m与Jx、Jy、Jz的值，采用Bushing(衬套)连接模拟发动机的原4点悬置和辅助悬置，并按表1中的主轴静刚度乘以动态系数1.3后输入主轴动刚度。同样的，在增加辅助悬置后，还应输入辅助悬置的主轴动刚度，由弹性解耦方程计算得出的刚度为静刚度，乘以动态系数1.3后即为辅助悬置的动刚度。

在重力作用下动力总成作自由振动，稳态时测量悬置的压缩变形量，测得无辅助悬置时前悬置变形量为2.4 mm，后悬置变形量为4.5 mm；增加辅助悬置后，前后悬置变形量均为3.2 mm。应用ADAMS/Vibration模块分析，得到系统的频率和能量分布。表3为无辅助悬置时的系统频率和能量分布，可以看出广义坐标z和θy分配的动能占系统总动能的比值分别为85.80%和85.83%，且两个广义坐标之间的耦合较大。表4为增加辅助悬置后的系统频率和能量分布，可以看出悬置系统固有频率略微提高，频率分布更合理，每个广义坐标之间的动能占系统总动能的比值均达到97.5%以上，其中广义坐标z和y之间的解耦效果显著。

表3无辅助悬置的系统固有频率和能量分布

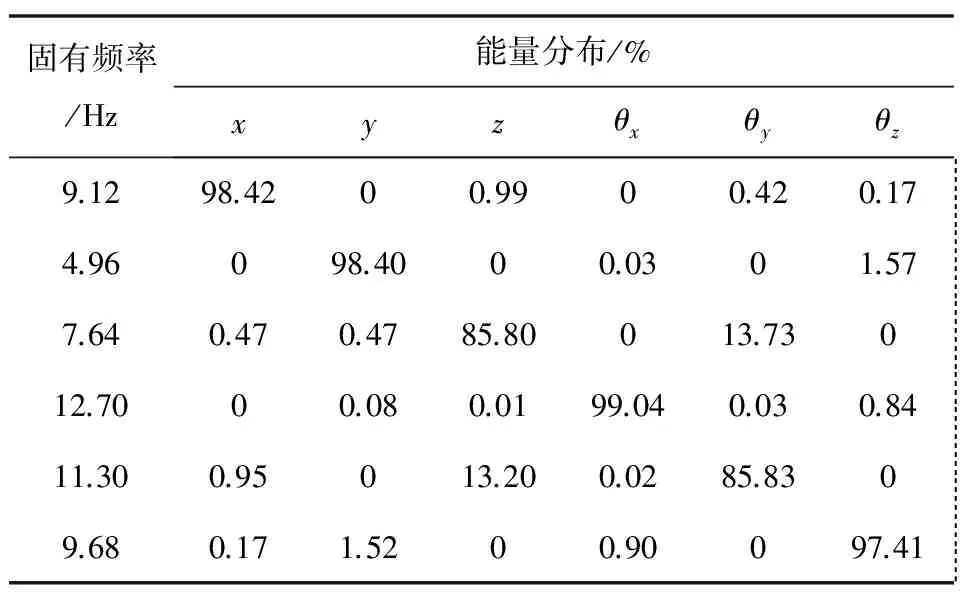
固有频率/Hz能量分布/%xyzθxθyθz9．1298．4200．9900．420．17 4．96098．4000．0301．57 7．640．470．4785．80013．730 12．7000．080．0199．040．030．84 11．300．95013．200．0285．830 9．680．171．5200．90097．41

表4 有辅助悬置的系统固有频率和能量分布

3 结语

应用拉格朗日方程建立动力总成振动系统关于6个自由度的振动微分方程，并推导出弹性解耦方程，在重型汽车要求装配缓速器或取力器等特殊情形下，发动机缸体后端面静弯矩大于设计允许值时，在变速器上增加辅助悬置，通过求解相应的解耦方程得到动力总成辅助悬置的刚度，在ADAMS软件中应用能量解耦法证明系统解耦效果良好。同时试验和用户使用情况表明，增加辅助悬置后车辆舒适性提高，螺母松动、橡胶块损坏等故障发生率减小，因此利用弹性解耦方程计算辅助悬置的刚度具有一定实际意义。