基于MMG模型的船舶动态扇形自动搜寻模式

吕蒙蒙，张强

(山东交通学院 航海学院，山东 威海 264209)

“海洋强国”和“一带一路”等国家战略的不断推进，为海运业的蓬勃发展带来了新的机遇，但同时也带来了一定的海上交通风险——海上事故时有发生[1]。海上事故一般离陆地较远，专业救助设备无法及时到达现场，附近船舶成为救助的主要力量。由于成本过高等原因，商船难以进行系统救助演习和训练。随着计算机仿真技术的发展，借助精确的船舶运动数学模型模拟搜救行动[2]，在没有特殊救助设备和缺乏正常训练的条件下，普通商船也可以按照海上搜寻与救助的常规方法进行救助[3]。

国内外研究者针对海上搜救进行了大量的研究，研究较多的是基于全球定位系统(GPS)的海上搜寻方法。文献[4-5]提出一种基于北斗卫星和自动识别系统(Automatic Identification System，AIS)通信系统的海上搜救方案，该方案在AIS无应答的范围内实现北斗网络系统的自动切换，并将SOS求救信号发送到北斗中心。文献[6]利用高频地波雷达等设备，实时更新海上风浪数据，并根据拉格朗日追踪法建立较简单的漂移动力学模型。文献[7-14] 研究了由上位机、无线传感器和地理信息系统(Geographic Information System,GIS)组成的搜救信息系统，并将搜救理论应用到该系统中。然而以上研究大多通过GPS确定搜救区域，并不间断推算受风、流等影响的实时位置，使搜救位置精度。本文在充分考虑航海实践要求的基础上，利用日本船舶操纵运动数学模型研究小组(Ship Manoeuvring Mathematical Model Group，MMG)的分离型船舶流体动力学数学模型，对船舶操纵运动进行非线性建模，充分考虑船舶惯性,流体黏滞系数和风、流等环境扰动的影响，构建真实有效的船舶仿真模拟系统。以一艘普通商船作仿真对象，利用Matlab软件中的Simulink模块对扇形搜寻模式进行仿真，验证所提搜寻模式的有效性。

1 扇形搜救模式

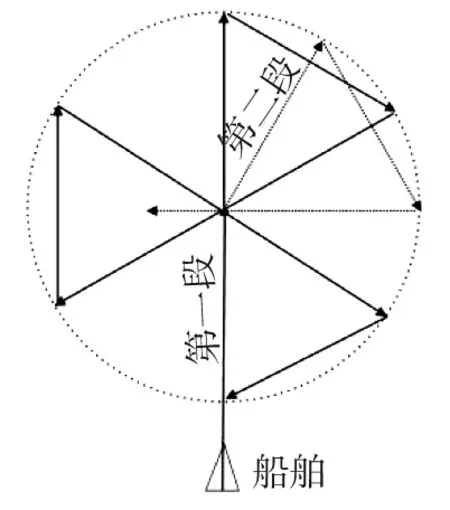
图1 扇形搜寻模式

扇形搜寻是一种单船搜寻方式。当搜寻目标区域较小时(例如人员落水或曾看到过搜寻目标但随后又丢失等情况)，宜采用扇形搜寻模式，而且发现目标的可能性也比较大[15]。该搜寻模式的半径通常为2～5 n mile，搜寻中船舶转向角度均为右转120°，分两段进行。前一段搜寻结束时(图1中实线航迹)，立刻右转30°，进入第二段搜寻(图1中虚线航迹)[16]。

2 数学模型的建立

船舶运动模型主要有两种[17]：一种是由Abkowitz等提出的整体型模型结构，将船、桨、舵视为一个不可分割的整体，研究船舶的受力情况，称作Abkowitz模型；另一种是MMG模型，将船舶的整体受力分解为船、桨、舵的单独受力及它们的相互影响，具有明确的物理意义，且通用性较强[18]。根据船舶运动控制的实际需要，本文以MMG分离模型为基础，在Simulink环境下建立一种结构合理、复杂程度适当的船舶平面运动数学模型。

2.1 MMG的数学模型

应用牛顿刚体力学的动量定理和动量矩定理，可得到如下数学模型：

式中：m为船舶质量；mx、my分别为船舶在纵向和横向的附加质量；Izz、Jzz分别为船舶的船体艏摇惯性矩及附加惯性矩；u、v、r分别为船舶纵向、横向速度矢量分量和转艏角速度；XH、Xp、XR分别为黏性类流体、桨和舵的纵向力；YH、YP、YR分别为黏性类流体、桨和舵的横向力；NH、Np、N分别为粘性类流体、桨和转艏力矩。

2.2 黏性类流体动力的确定

采用贵岛模型[18]近似估算黏性流体动力：

(2)

式中：Xu为直航阻力；Xvv、Xvr和Xrr为纵向流体动力系数；Yv、Yr、Nv和Nr为线性流体水动力系数；Yvvr、Yvrr、Nvvr、Nvrr、Y|v|v、Y|r|r、N|v|v和Y|r|r为非线性流体水动力系数。

2.3 非线性流体动力导数的近似估算公式

贵岛近似估算公式[19]：

2.4 舵机特性模型

船舶舵机伺服系统具有纯滞后、死区、饱和等非线性特性，因此在考虑舵机执行舵角以及转舵速度的限制外，为了体现模型中由于无量纲化导致的超大型船舶惯性的衰减，还应根据船舶吨位适当延迟船舶的应舵时间。

通常描述舵机执行舵角以及转舵速度的模型为：

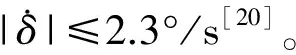
3 Simulink仿真模型的建立

根据单船舶扇形搜寻的模式，在MATLAB中Simulink模块下，运用已经建立好的船舶运动数学模型，构建扇形搜寻的仿真模型，如图2所示。

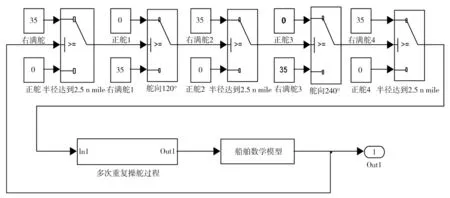
图2 仿真模型框架图

模型仿真中初始航速5 kn，初始航向0°，搜索半径为2.5 n mile，以在船舶初始位置向北2.5 n mile处为定位基点开始仿真。船舶向正北航行，当到达离基点2.5n mile的搜寻边界时转向120°，当下一次达到搜寻边界时再次转向后直航，驶过基点，达到边界时转向，直到完成第一遍的搜寻。当第一遍搜寻结束又一次驶过基点时，航向改为30°，重复第一遍搜寻的步骤。模拟的船舶参数如表1所示。

表1 船舶参数

搭建的MMG数学模型需要充分体现操作与反馈之间的相互影响。该模型是对船舶搜寻真实场景的模拟，而简单的Simulink难以直接对由船体、舵、桨等组成的具有强非线性的船舶转向系统进行精确模拟。因此，为了使仿真既体现航海实践中的真实场景，又简捷有效、易于工程实现，船舶操舵试验要求舵机自一舷35°转舵至另外一舷30°所需要的时间不应该超过28 s[9]，并考虑到航海中受风、流等影响可能会导致转向变慢等不利局面，因此在Simulink转向模型中加入了30 s的延时，使仿真更加接近实际情况。在整个搜寻过程中由于转向的不断变化，导致航速是时变的，故需要根据不同的船舶初始状态进行参数修正，以便船舶能够真实有效的抵达预定航向。表2为船舶在5 kn的航速下，所采取的行动与所达到的效果对比(只展示了第一遍搜寻)。

表2 操舵时机与实际效果对比表

4 仿真结果

由于扇形搜寻的过程大致为重复过程，所以本模型仅模拟了第一遍搜寻以及第二遍搜寻的一小部分。在Simulink环境下进行仿真试验的船舶航行轨迹如图3所示。为了能够更好的反映整个扇形搜寻的船舶运动过程，利用Simulink模型中的示波器模块，实时记录下舵角(angle of rudder)、船舶航速(U speed)、纵向速度(V speed)以及航向(course)的变化曲线，如图4～6所示。

图3 船舶运动轨迹 图4 舵角变化趋势图

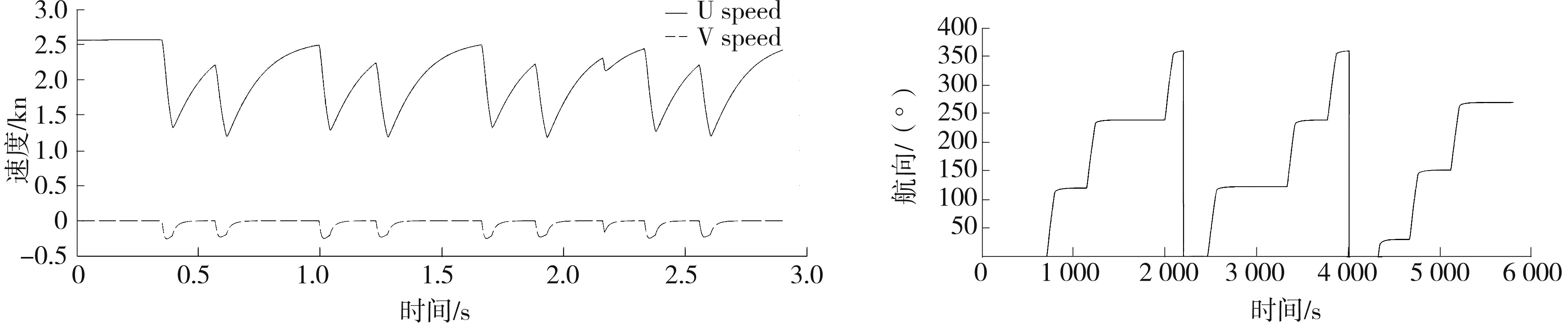
图5 航速及纵向速度变化趋势图 图6 航向变化趋势图

图4为扇形搜寻模式中搜救船舶的舵角变化趋势图。从图4可以看出：在搜寻过程中，船舶开始保持正舵，在达到预定的区域范围或者航向时，改变舵角即可。而且只是不停的在正舵和满舵之间转换，操作并不复杂，前提条件是风浪作用很小。

图5为船舶在扇形搜寻中，航速以及船舶纵向速度的变化趋势。由图5可知，由于船舶在水中受到的阻力，船舶的航速在转向时大幅度降低，在直航时增加。在扇形搜寻模式中，搜救船舶不停的进行转向运动，所以船舶航速不停的变化，即在直航中加速，在转向中减速。在整个搜寻运动中，船舶的平均航速不能始终达到初始航速。要提高平均速度，就必须提高船舶的初始速度。因为船舶在搜寻活动中始终向右转舵，所以只出现负的纵向速度。而在直航时没有纵向速度。

图6为船舶在扇形搜寻模式中航向的变化。搜救船舶在搜寻中只有简单的几个航向，由于船舶在实际操纵中的困难，或者驾驶人员对转向实际的把握不够准确，航向会出现一定的偏差。但微小偏差并不影响实际过程中的搜救行动。

5 结语

海上人命安全一直以来是海上运输中最重视的一个环节。由于海上搜救是一个复杂而且庞大的工程，在实际中很难模拟，而且搜救演习耗资巨大，不可能经常进行，并具有一定的风险。计算机模拟仿真就很好的解决了这方面的问题。

本文利用MMG船舶运动数学模型构建的扇形搜索模式，通过仿真得到了船舶在搜寻过程中航向、舵角、航速等参数，均符合航海实际要求。这些参数可为船舶实际搜救提供参考数据，并为协助船舶脱离危险提供技术支持。本研究融合了风、浪、流等外界扰动的影响，不需要额外进行风流等漂流模型的推算，因此可提高船舶应对突发事故的搜救能力，对于完善和研发海事搜救无人艇、船舶搜救信息系统及船舶应急响应服务系统，具有重要的参考意义。